文档内容
内江市高中 2024 届第三次模拟考试
数 学( 文科)
本试卷包括第卷(选择题)和第卷(非选择题)两部分,共页。全卷满分 分,考试
1. Ⅰ Ⅱ 4 150
时间 分钟。
120
答第卷时,用 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,
2. Ⅰ 2B
再选涂其它答案标号;答第卷时,用 毫米的黑色签字笔在答题卡规定的区域内作答,字体工
Ⅱ 0.5
整,笔迹清楚;不能答在试题卷上。
考试结束后,监考员将答题卡收回。
3.
第卷(选择题,共 分)
Ⅰ 60
一、选择题(本大题共小题,每小题分,共 分在每个小题所给出的四个选项中,只有一
12 5 60 .
项是符合题目要求的)
.
集合 { x-2 , }的子集个数是
1. P= x| ≤0 x∈Z
x+1
A.5 B.6 C.7 D.8
已知是虚数单位, 1 +3i,则·
2. i z= z 珋z=
2 +i
槡
A.1 +i B.1 -i C.2 D. 2
已知向量 (, ), ( , ),若 ,则sinα-cosα的值为
3. 珗a= 1 -2 b珒= cosα sinα 珗a⊥b珒
sinα+cosα
1 2 1 2
A B. C. - D. -
3 3 3 3
三个不互相重合的平面将空间分成个部分,则的最小值与最大值之和为
4. n n
A.11 B.12
C.13 D.14
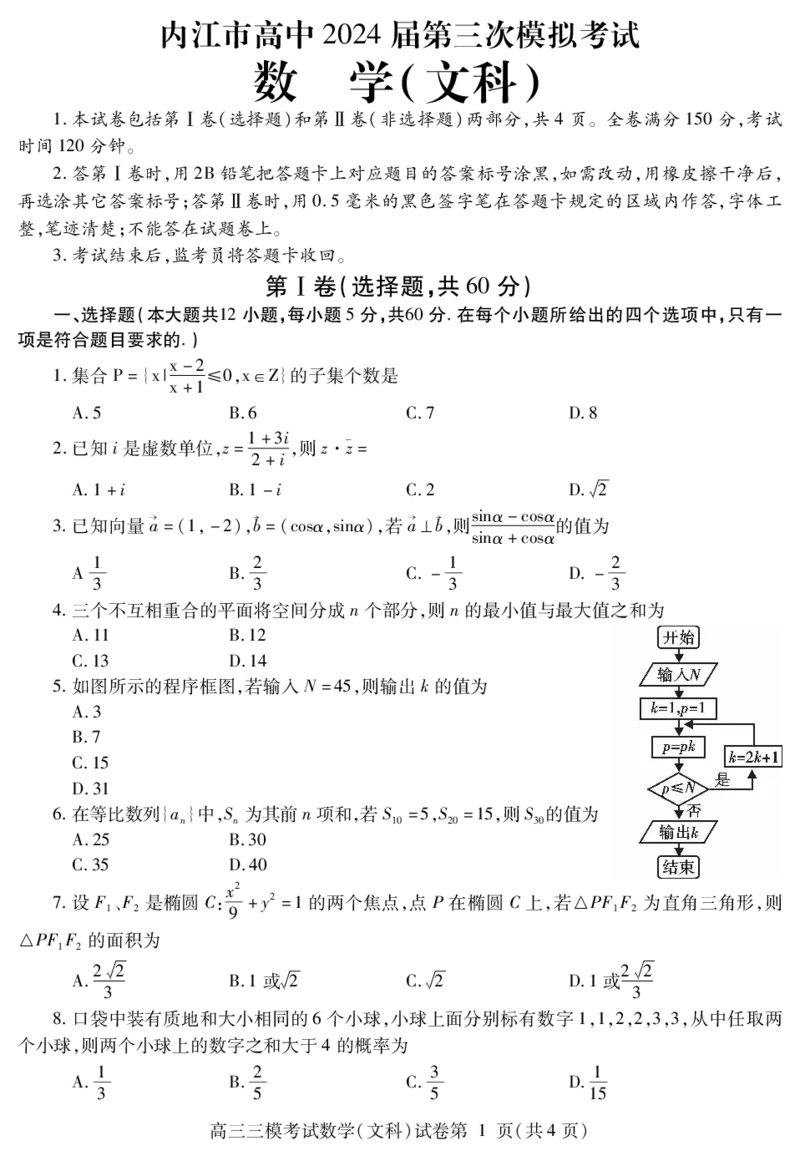
如图所示的程序框图,若输入 ,则输出的值为
5. N=45 k
A.3
B.7
C.15
D.31
在等比数列{ }中, 为其前项和,若 , ,则 的值为
6. a S n S =5 S =15 S
n n 10 20 30
A.25 B.30
C.35 D.40
设、 是椭圆:x2 的两个焦点,点在椭圆上,若 为直角三角形,则
7. F F C +y2 =1 P C △PF F
1 2 9 1 2
的面积为
△PF F
1 2
槡 槡
2 2 或槡 槡 或2 2
A. B.1 2 C. 2 D.1
3 3
口袋中装有质地和大小相同的个小球,小球上面分别标有数字,,,,,,从中任取两
8. 6 1 1 2 2 3 3
个小球,则两个小球上的数字之和大于的概率为
4
1 2 3 1
A. B. C. D.
3 5 5 15
高三三模考试数学(文科)试卷第 页(共页)
1 4
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}已知正方体 的棱长为,点、、 分别为棱 、 、 的中点,则平
9. ABCD-A B C D 2 M N P AB CC C D
面 截正方体所得截面的1面1积1为1 1 1 1
MNP
槡
3 槡 槡 槡
A. B.3 3 C.6 2 D. 3
2
若函数() lnx x 有两个零点,则实数的取值范围为
10. f x = - m
x m
(,) (, ) (, ) ( , )
A. 0 e B. e +∞ C. 0 2e D. 2e +∞
已知双曲线:x2 y2 ( , ),以双曲线的右顶点为圆心,为半径作圆,圆
11. C - =1 a>0 b>0 C A b A
a2 b2
与双曲线的一条渐近线交于、 两点,若→ 1 →,则双曲线的离心率为
A C M N OM= ON
3
槡 槡
槡 槡 2 3 6
A. 2 B. 3 C. D.
3 2
已知函数()的定义域为,对 , 都有( )( ) ( ) ( )成
12. f x R x y∈R 2f x +1 f y +1 =f x +y -f x -y
立,若() ,则( )
f 0 ≠0 f 2024 =
A. -1 B.0 C.1 D.2
第卷(非选择题,共 分)
Ⅱ 90
二、填空题(本大题共小题,每小题分,共 分)
4 5 20 .
已知函数() ,则函数()在 处的切线方程为
13. f x =ex +sinx f x x=0 .
,
{4x-y-1≤ 0
已知实数,满足 ,则 的最大值为
14. x y 4x+y+1≥0 z=2x-y .
x-y+2≥0.
, ,
若函数() {x2 +ax x≥0 是奇函数,则
15. f x = , a+b= .
bx2 -2x x<0.
在 中,角的平分线 与 边相交于点,若 7 ,则AB+AC的最小值为
16. △ABC A AD BC D cosA =
9 AD
.
三、解答题(本大题共小题,共 分,解答应写出文字说明、证明过程或演算步骤,第
6 70 17 ~21
题为必考题,每个试题考生都必须作答,第、 题为选考题,考生根据要求作答)
22 23 .
(本小题满分 分)
17. 12
年月 日至 日(正月初一至初八),“ ·内江市中区新春极光焰火草地狂欢节”
2024 2 10 17 2024
在川南大草原举行,共举行了场精彩的烟花秀节目前场的观众人数(单位:万人)与场次的统
8 . 5
计数据如表所示:
场次编号
x 1 2 3 4 5
观众人数
y 0.7 0.8 1 1.2 1.3
()已知可用线性回归模型拟合与的关系,请建立关于的线性回归方程;
1 y x y x
()若该烟花秀节目分、、 三个等次的票价,某机构随机调查了该烟花秀节目现场 位
2 A B C 200
观众的性别与购票情况,得到的部分数据如表所示,请将 列联表补充完整,并判断能否有
2 ×2
的把握认为该烟花秀节目的观众是否购买等票与性别有关
90% A .
高三三模考试数学(文科)试卷第 页(共页)
2 4
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}购买等票 购买非等票 总计
A A
男性观众
50
女性观众
60
总计
100 200
参考公式及参考数据:回归方程 ∧ ∧ ∧ 中斜率与截距的最小二乘法估计公式分别为
y =bx+a
n ( )( )
∧ b =i ∑ =1 x i -x珋 y i -y珋 , ∧ a =y珋- ∧ bx珋 , K2 =( )( n ( ad ) - ( bc ) 2 )( ) ,其中 n=a+b+c+d.
n ( ) a+b c+d a+c b+d
∑ x -x珋2
i
i=1
( )
P K2≥k 0.100 0.050 0.010
k 2.706 3.841 6.635
(本小题满分 分)
18. 12
已知等差数列{ }的公差为,且 , , 成等比数列,数列{ }的前项和为,
a 4 a +2 a a -2 b n S
且 n( ) 2 3 5 n n
b =2 S =2S +2 n≥2 .
1 ()求n数列n{-1 }、{ }的通项公式;
1 a b
()设 n ( n ),求数列{ }的前项和
2 c =a b n∈N c n T .
n n n n n
(本小题满分 分)
19. 12
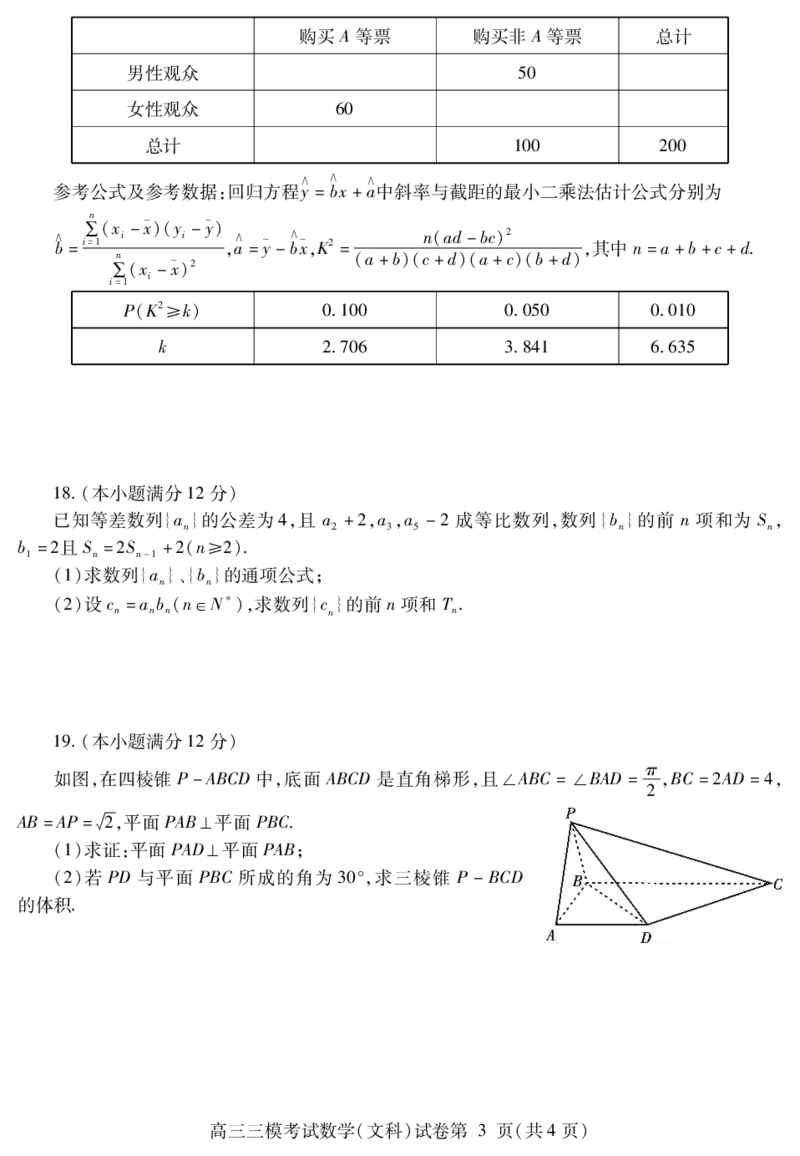
如图,在四棱锥 中,底面 是直角梯形,且 π, ,
P-ABCD ABCD ∠ABC =∠BAD = BC =2AD =4
2
槡,平面 平面
AB=AP= 2 PAB⊥ PBC.
()求证:平面 平面 ;
1 PAD⊥ PAB
()若 与平面 所成的角为 ,求三棱锥
2 PD PBC 30° P -BCD
的体积
.
高三三模考试数学(文科)试卷第 页(共页)
3 4
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}(本小题满分 分)
20. 12
已知函数() (1 ),
f x =lnx+a -1 a>0.
x
()若() 恒成立,求的取值集合;
1 f x ≥0 a
()证明:1 1 …1 ( )
2 + + + <ln3 n∈N .
n+1 n+2 3n
(本小题满分 分)
21. 12
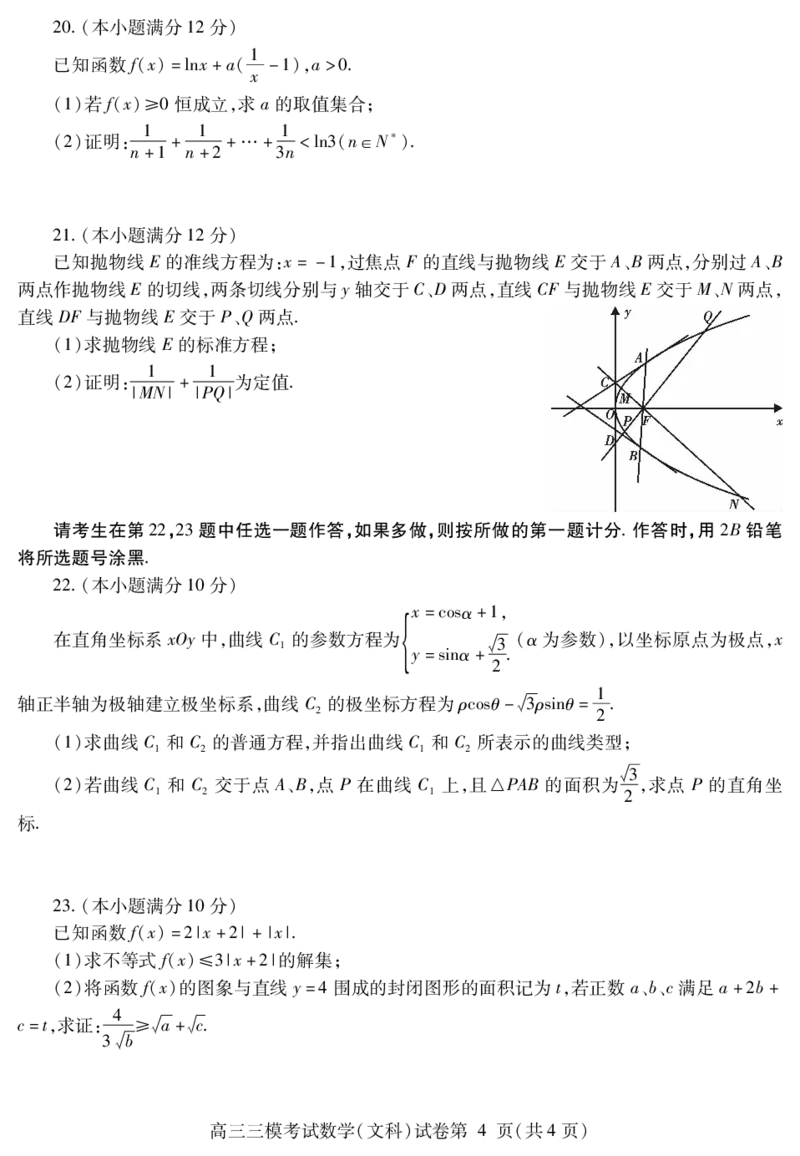
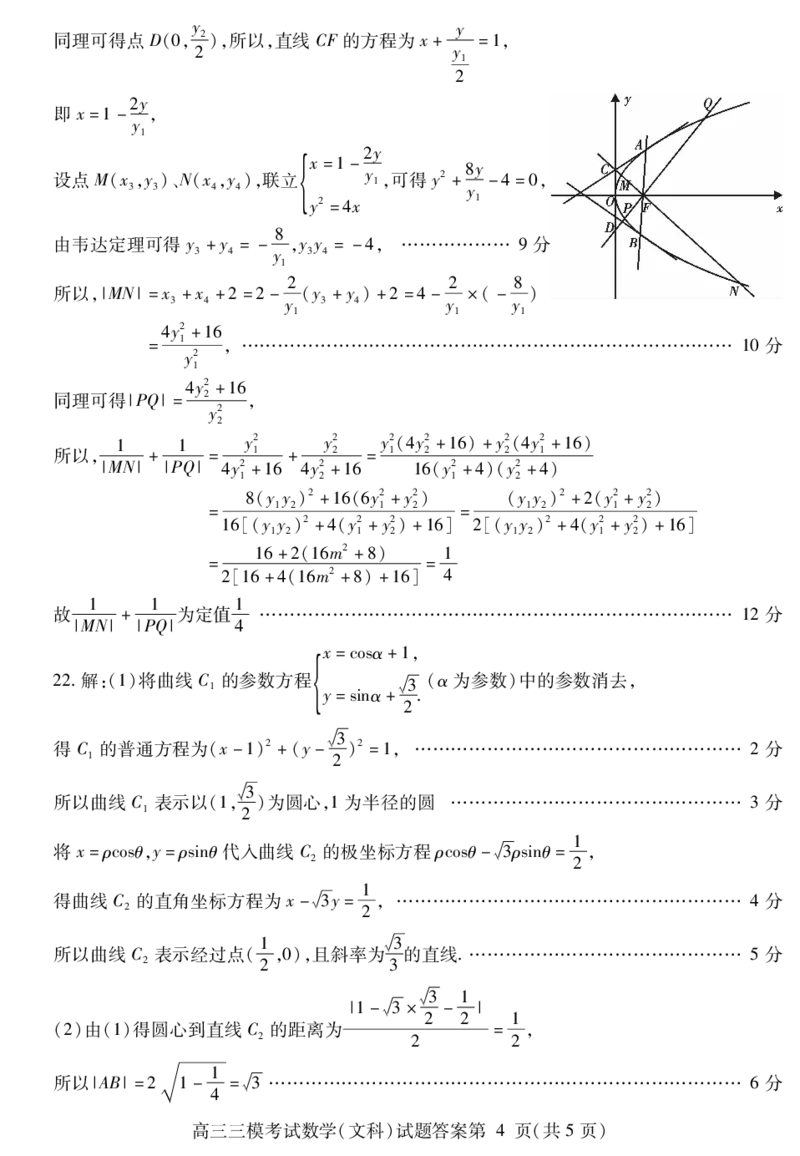
已知抛物线的准线方程为: ,过焦点的直线与抛物线交于、 两点,分别过、
E x= -1 F E A B A B
两点作抛物线的切线,两条切线分别与轴交于、 两点,直线 与抛物线交于、 两点,
E y C D CF E M N
直线 与抛物线交于、 两点
DF E P Q .
()求抛物线的标准方程;
1 E
()证明: 1 1 为定值
2 + .
|MN| |PQ|
请考生在第, 题中任选一题作答,如果多做,则按所做的第一题计分作答时,用 铅笔
22 23 . 2B
将所选题号涂黑
.
(本小题满分 分)
22. 10
,
{x=cosα+1
在直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点,
槡
xOy C 1 3 α x
y=sinα+ .
2
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为 槡 1
C ρcosθ- 3ρsinθ= .
2 2
()求曲线 和 的普通方程,并指出曲线 和 所表示的曲线类型;
1 C C C C
1 2 1 2
槡
()若曲线 和 交于点、,点在曲线 上,且 的面积为3,求点的直角坐
2 C C A B P C △PAB P
1 2 1 2
标
.
(本小题满分 分)
23. 10
已知函数()
f x =2|x+2| + |x|.
()求不等式() 的解集;
1 f x ≤3|x+2|
()将函数()的图象与直线 围成的封闭图形的面积记为,若正数、、满足
2 f x y=4 t a b c a+2b +
,求证:4 槡槡
c=t 槡≥ a + c.
3 b
高三三模考试数学(文科)试卷第 页(共页)
4 4
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}内江市高中 2024 届第三次模拟考试
数学(文科)参考答案及评分意见
一、选择题(本大题共 小题,每小题分,共 分)
12 5 60 .
1.D 2.C 3.C 4.B 5.C 6.C 7.D 8.A 9.B 10.D 11.D 12.A
二、填空题(本大题共小题,每小题分,共 分)
4 5 20 .
槡
3 2
13.y=2x+1 14.1 15. -3 16.
2
三、解答题(本大题共小题,共 分)
6 70
解:()由表格知 1 +2 +3 +3 +5 , 分
17. 1 x珋= =3 !!!!!!!!!!!!!!!!!! 1
5
0.7 +0.8 +1 +1.2 +1.3 , 分
y珋= =1 !!!!!!!!!!!!!!!!!!!!!!! 2
5
所以5 ( ) ( ) ( ) ,
∑ x -x珋2 = -2 2 + -1 2 +0 +12 +22 =10
i
i=1
5 ( )( ) ( ) ( ) ( ) ( ) ,
∑ x -x珋 y -y珋 = -2 × -0.3 + -1 × -0.2 +0 ×0 +1 ×0.2 +2 ×0.3 =1.6
i i
i=1
5 ( )( )
则∧ ∑ x i -x珋 y i -y珋 1.6 , 分
b =i=1 = =0.16 !!!!!!!!!!!!!!!!!!!!! 4
5 ( ) 10
∑ x -x珋2
i
i=1
, 分
∧
a =1 -0.16 ×3 =0.52 !!!!!!!!!!!!!!!!!!!!!!!!!!! 5
故关于的线性回归方程为 分
∧
y x y =0.16x+0.52. !!!!!!!!!!!!!!!!! 6
()依题意,补充 列联表如下:
2 2 ×2
购买等票 购买非等票 总计
A A
男性观众
40 50 90
分
女性观众 !!!!!!!!!!! 8
60 50 110
总计
100 100 200
( )
200 × 60 ×50 -40 ×50 2 分
K2 = ≈2.020 <2.706 !!!!!!!!!!!!!!!!! 10
90 ×110 ×100 ×100
故没有 的把握认为该节目的观众是否购买等票与性别有关 分
90% A . !!!!!!!! 12
解:()依题意,设等差数列{ }的首项为,因为 , , 成等比数列,
18. 1 a a a +2 a a -2
所以 ( )( ),又 n ,即( )1 ( 2 )( 3 5 ),解得 , 分
a2 = a +2 a -2 d=4 a +8 2 = a +6 a +14 a = -5 ! 1
故 3 (2 )5 ( ) 1 , 1 1 1 分
a =a + n-1 d= -5 +4 n-1 =4n-9 !!!!!!!!!!!!!!!!! 3
由已n知1 ( ),
S =2S +2 n≥2
故 n n-,1
S =2S +2
两式n相+1减,得n ( ), 分
b =2b n≥2 !!!!!!!!!!!!!!!!!!!!!!!! 4
又 ,n解+1得n ,所以 , 分
S =2S +2 b =4 b =2b !!!!!!!!!!!!!!!!!!!! 5
所以2数列{1 }是以为2 首项,为公2 比的1 等比数列,故 · 分
b 2 2 b =2 2n-1 =2n !!!!!!! 6
n n
高三三模考试数学(文科)试题答案第 页(共页)
1 5
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}()由()得 ( )·,故 …( )·,
2 1 c =a b = 4n-9 2n T = -5 ×21 -1 ×22 +3 ×23 + + 4n-9 2n
则 n n n …(n ) 分
2T = -5 ×22 -1 ×23 -3 ×24 + + 4n-9 ×2n+1 !!!!!!!!!!!!!! 8
两式相n 减得 ( … ) ( ) 分
-T = -10 +4 22 +23 + +2n - 4n-9 ×22n+1 !!!!!!!!!! 9
n ( )
22 1 -2n-1 ( ) 分
= -10 +4 × - 4n-9 ×22n+1 !!!!!!!!!!! 10
1 -2
( ) , 分
= 13 -4n ×2n+1 -26 !!!!!!!!!!!!!!!!!!! 11
故 ( ) 分
T = 4n-13 ×2n+1 +26 !!!!!!!!!!!!!!!!!!!!!!!! 12
解n :()证明:取 的中点,连接
19. 1 PB M AM.
, 分
∵ AB=AP ∴ AM⊥PB. !!!!!!!!!!!!!! 1
又平面 平面 ,平面 平面 , 平面
PAB⊥ PBC PAB∩ PBC =PB AB
,
PAB
平面 分
∴ AM⊥ PBC. !!!!!!!!!!!!!!!! 2
又 平面 ,
BC PBC
分
∴ AM⊥BC. !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 3
底面 是直角梯形,且 π
∵ ABCD ∠ABC=∠BAD=
2
,
∴ BC∥AD ∴ AD⊥AM.
又 , ,
AD⊥AB AM∩AB=A
平面 分
∴ AD⊥ PAB.!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 4
又 平面 ,
AD PAD
平面 平面 分
∴ PAD⊥ PAB. !!!!!!!!!!!!!!!!!!!!!!!!!!! 5
()取 的中点,连接 、 ,则 1 ,
2 PC N MN DN MN= BC=AD MN∥BC∥AD.
2
四边形 是平行四边形,则
∴ AMND DN∥AM.
又 平面 , 平面 ,则 是 与平面 所成的角,
AM⊥ PBC ∴ DN⊥ PBC ∠DPC PD PBC
即 , 分
∠DPC=30° !!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 7
在 中,易知 槡 槡 分
Rt△PAD PD= AD2 +AP2 = 6. !!!!!!!!!!!!!!!!!! 8
在直角梯形 中,易知 槡, , ,
ABCD CD= 6 ∴ CD=PD ∴ ∠DCP=∠DPC=30°
槡
槡 3 槡, 分
∴ PC=2 × 6 × =3 2 !!!!!!!!!!!!!!!!!!!!!!!!!! 9
2
在 中, 槡 槡,
Rt△PBC PB= PC2 -BC2 = 2
槡
是等边三角形从而 6 分
∴ △PAB . AM=DN= !!!!!!!!!!!!!!!!!! 10
2
槡 槡
1 1 (1 槡) 6 2 3
∴ V = ×S ×DN= × ×4 × 2 × = .
P-BCD 3 △PBC 3 2 2 3
槡
故所求三棱锥 的体积为2 3 分
P-BCD !!!!!!!!!!!!!!!!!!!!! 12
3
解:()由题可知函数()的定义域为{ },
20. 1 f x x|x>0
() 1 a x-a,
∵ f′ x = - =
x x2 x2
高三三模考试数学(文科)试题答案第 页(共页)
2 5
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}当 时,() ,()递减,
∴ 0 <x<a f′ x <0 f x
当 时,() ,()递增,
x>a f′ x >0 f x
() () , 分
∴ f x =f a =lna-a+1 !!!!!!!!!!!!!!!!!!!!!!!!! 2
由已知min() 恒成立,所以 , (, )
f x ≥0 lna-a+1≥0 a∈ 0 +∞ .
令() ,则() 1 1 -x, 分
g x =lnx-x+1 g′ x = -1 = !!!!!!!!!!!!!!!!! 3
x x
当 时, () ,()递增,
∴ 0 <x<1 g′ x >0 g x
当 时, () ,()递减,
x>1 g′ x <0 g x
() () 分
∴ g x =g 1 =0 !!!!!!!!!!!!!!!!!!!!!!!!!!!! 4
又 m(ax ,),() () ,
∵ a∈ 0 1 g a =lna-a+1 <g 1 =0
(, ),() () ,
a∈ 1 +∞ g a =lna-a+1 <g 1 =0
,故的取值集合为{} 分
∴ a=1 a 1 . !!!!!!!!!!!!!!!!!!!!!!!! 6
()由()可知,当 时,() ,即 1 , 1 x-1, 分
2 1 a=1 f x ≥0 lnx+ -1≥0 lnx≥1 - = !!!!! 7
x x x
( ) x (当 时,“ ”成立),令 1 ( ),
∴ ln x+1 ≥ x=0 = x= n∈N
x+1 n
1
(1 ) n 1 ,则(n+1) 1 ,即( ) 1 , 分
ln +1 > = ln > ln n+1 -lnn> !!!!! 8
n 1 n+1 n n+1 n+1
+1
n
故( ) ( ) 1 ,( ) ( ) 1 ,…,( ) ( ) 1 ,
ln n+2 -ln n+1 > ln n+3 -ln n+2 > ln 3n -ln 3n-1 >
n+2 n+3 3n
由累加法可得( ) 1 1 1 …1 , 分
ln 3n -lnn> + + + + !!!!!!!!!!!! 10
n+1 n+2 n+3 3n
即1 1 1 …1 分
+ + + <ln3 !!!!!!!!!!!!!!!!!!!!!! 12
n+1 n+2 n+3 3n
解:()因为准线为: ,设 ,则p 分
21. 1 x= -1 y2 =2px - = -1 !!!!!!!!!!!!! 2
2
所以
p=2
故抛物线的标准方程为 分
E y2 =4x !!!!!!!!!!!!!!!!!!!!!!! 3
()证明:易知抛物线的焦点(,),
2 E F 1 0
设直线 的方程为 ,( , )、( , ),联立{y2 =4x 可得 ,
AB x=my+1 A x y B x y y2 -4my-4 =0
1 1 2 2 x=my+1
由韦达定理可得 , , 分
y +y =4m y y = -4 !!!!!!!!!!!!!!!!!!!! 4
接下来证明抛物线1 在2 点处1的2切线方程为 ,
E A y y=2x+2x
1 1
联立{y2 =4x 可得 ,即 ,即( ) ,
y2 -2y y+4x =0 y2 -2y y+y2 =0 y-y 2 =0
y y=2x+2x 1 1 1 1 1
所以,直1线 1 与抛物线只有唯一的公共点,
y y=2x+2x E
所以, 的方1 程为 1 , 分
AC y y=2x+2x !!!!!!!!!!!!!!!!!!!!!!! 6
同理可知,直线 的1 方程为1 ,
BD y y=2x+2x
2 2
y2
2 × 1
在直线 的方程中,令 ,可得 2x 4 y ,即点(,y ), 分
AC x=0 y= 1 = = 1 C 0 1 !!!!!! 8
y y 2 2
1 1
高三三模考试数学(文科)试题答案第 页(共页)
3 5
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}同理可得点(,y ),所以,直线 的方程为 y ,
D 0 2 CF x+ =1
2 y
1
2
即 2y,
x=1 -
y
1
{ 2y
设点( , )、( , ),联立x=1 - ,可得 8y ,
M x 3 y 3 N x 4 y 4 y 1 y2 + y -4 =0
y2 =4x 1
由韦达定理可得 8 , , 分
y +y = - y y = -4 !!!!!! 9
3 4 y 3 4
1
所以, 2 ( ) 2 ( 8 )
|MN| =x +x +2 =2 - y +y +2 =4 - × -
3 4 y 3 4 y y
1 1 1
4y2 +16, 分
= 1 !!!!!!!!!!!!!!!!!!!!!!!!!!! 10
y2
1
同理可得 4y2 +16,
|PQ| = 2
y2
2 ( ) ( )
所以, 1 1 y2 y2 y2 4y2 +16 +y2 4y2 +16
+ = 1 + 2 = 1 2( )(2 1)
|MN| |PQ| 4y2 +16 4y2 +16 16 y2 +4 y2 +4
1 ( )2 ( ) 1 (2 ) ( )
8 y y 2 +16 6y2 +y2 y y 2 +2 y2 +y2
= [(1 2) ( 1 )2 ]= [( 1)2 ( 1 )2 ]
16 y y 2 +4 y2 +y2 +16 2 y y 2 +4 y2 +y2 +16
1 2 ( 1 )2 1 2 1 2
16 +2 16m2 +8 1
= [ ( ) ]=
2 16 +4 16m2 +8 +16 4
故1 1 为定值1 分
+ !!!!!!!!!!!!!!!!!!!!!!!!!! 12
|MN| |PQ| 4
,
{x=cosα+1
解:()将曲线 的参数方程 ( 为参数)中的参数消去,
槡
22. 1 C 1 3 α
y=sinα+ .
2
槡
得 的普通方程为( ) ( 3) , 分
C x-1 2 + y- 2 =1 !!!!!!!!!!!!!!!!!! 2
1 2
槡
所以曲线 表示以(,3)为圆心,为半径的圆 分
C 1 1 !!!!!!!!!!!!!!!! 3
1 2
将 , 代入曲线 的极坐标方程 槡 1 ,
x=ρcosθ y=ρsinθ C ρcosθ- 3ρsinθ=
2 2
得曲线 的直角坐标方程为 槡 1 , 分
C x- 3y= !!!!!!!!!!!!!!!!!!! 4
2 2
槡
所以曲线 表示经过点(1 ,),且斜率为3的直线 分
C 0 . !!!!!!!!!!!!!!! 5
2 2 3
槡
槡 3 1
|1 - 3 × - |
()由()得圆心到直线 的距离为 2 2 1 ,
2 1 C =
2 2 2
槡
所以 1 槡 分
|AB| =2 1 - = 3 !!!!!!!!!!!!!!!!!!!!!!!!!! 6
4
高三三模考试数学(文科)试题答案第 页(共页)
4 5
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}槡
设点( , 3),
P cosα+1 sinα+
2
( π)
槡 |2cos α+ -1|
则点到直线 的距离 |cosα- 3sinα-1| 3
P C d= = .
2 2 2
( π)
槡 |2cos α+ -1| 槡
因为 的面积为3,所以1 槡 3 3 分
△PAB × 3 × = . !!!!!!!!!! 8
2 2 2 2
所以 ( π) ,则 ( π) 1 或 ( π) 3 (舍去),
|2cos α+ -1| =2 cos α+ = - cos α+ =
3 3 2 3 2
所以 π 2π ,或 π 4π , ,所以 π 或 , ,
α+ = +2kπ α+ = +2kπ k∈Z α= +2kπ α=π+2kπ k∈Z
3 3 3 3 3
分
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 9
槡
点的直角坐标为(3 ,槡)或(,3) 分
P 3 0 !!!!!!!!!!!!!!!!!!!!! 10
2 2
()由 可得 , 分
23. 1 2|x+2| + |x|≤3|x+2| |x|≤|x+2| !!!!!!!!!!!!!!! 2
即 ( ),解得 分
x2≤ x+2 2 x≥-1 !!!!!!!!!!!!!!!!!!!!!!!!! 4
所以不等式的解集为[ , ) 分
-1 +∞ !!!!!!!!!!!!!!!!!!!!!!! 5
,
{ -3x-4 x≤-2
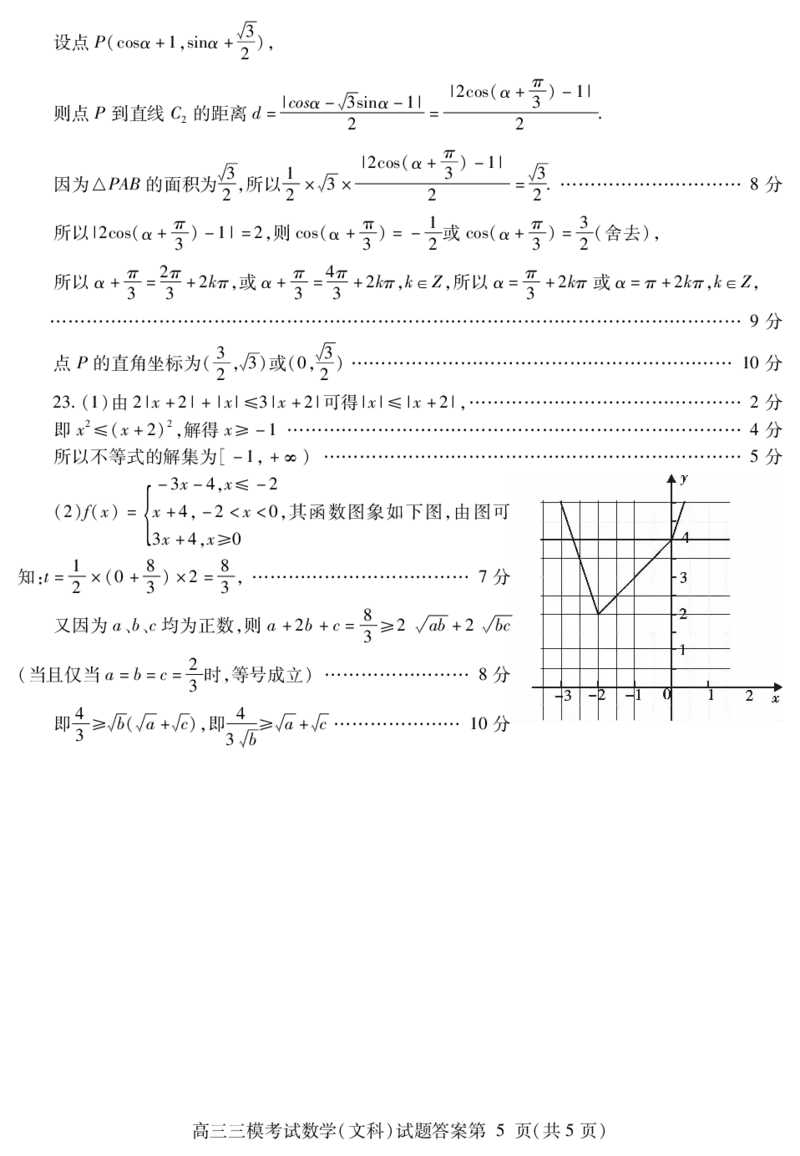
()() , ,其函数图象如下图,由图可
2 f x = x+4 -2 <x<0
,
3x+4 x≥0
知: 1 ( 8 ) 8 , 分
t= × 0 + ×2 = !!!!!!!!!!!! 7
2 3 3
又因为、、均为正数,则 8 槡 槡
a b c a +2b +c = ≥2 ab +2 bc
3
(当且仅当 2 时,等号成立) 分
a=b=c= !!!!!!!! 8
3
即4 槡(槡槡),即4 槡槡 分
≥ b a + c 槡≥ a + c !!!!!!! 10
3 3 b
高三三模考试数学(文科)试题答案第 页(共页)
5 5
{{##{{QQQQAABBACYYCSU95oggggwgAgIITBAACABB5gqCQQUQ232CCCAAiQGkQJKkAgELEAoCMAAoGVCBGFAqAMwMDACAZBNSARBNIAAB=}A#A}=}#}