四川省成都市成华区某校2024届高三下学期三诊试题数学（文）含答案(1)_2024年5月_025月合集_2024届四川成都列五中学高三下学期三诊

高三三诊模拟考试数文
一、选择题：本题共12小题，每小题 5分，共60分.在每小题给出的四个选项中，只
有一项是符合题目要求的.
 
1．已知集合A xx2 2x30 ，B{x|3x1 1}，则AB=（ ）
（A） (1，1] （B） [1，3] （C） (1，3] （D） [3，)
2．已知一样本数据（如茎叶图所示）的中位数为12，若 ， 均
x y
小于4，则x y 的值为 （ ）
（A） 2 （B） 3 （C） 4 （D） 5
3．已知角 的顶点在坐标原点，始边与 轴非负半轴重合， ， 为其终边
5
上一点，  则 ( )  cos  = 5  (  ,2)
（A） （B） （C） （D）
=
4. 已知 −4 ， ，4 ，则( ) −1 1
1 
（A）  = log52  = log2   = (2) （B）
（C） （D）
>  >   >  > 
>  >   >  > 
y
5.若实数 ， 满足约束条件 则 的最大值为( )
−  −1 ≥ 0,
x
+  −3 ≤ 0,

（A） （B）  ≥ 0. （C） （D）
1 1
0 3 2 2
6.“中国剩余定理”又称“孙子定理”， 年英国来华传教士伟烈亚力将《孙子算
1852
经》中“物不知数”问题的解法传至欧洲 年英国数学家马西森指出此法符合
年由高斯得出的关于同余式解法的一.1般8性74定理，因而西方称之为“中国剩余定
理”，“中国剩余定理”讲的是一个关于同余的问题现有这样一个问题：将正整数中
1801
能被 除余 且被 除余 的数按由小到大的顺序排成一列，构成数列 ，则
.
3 ( ) 1 2 1  

（10A）
=
（B） （C） （D）
7.如图，在三棱柱 中， ， ， ， 分别为 ， ， ， 的中
55 49 43 37
点，则下列说法  错  误  的 − 是  1  (1  1 )       1   1  1  1  1  1
（A） ， ， ， 四点共面 （B）
//  
高三“三诊”模拟数学试题（文科） 第 页 共 页
1 4
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#}（C） ， ， 三线共点 （D） ∠ ∠
8. 若     是  不  等1 式 成立的一  个   必1要=不充   分  条1 件，
1
则实  数<  的<取3值范围是(log2  )>−1
（A）  ∞ （B） ∞ （C） （D）
(− ,0) (− ,0] [0,2) (2,3)
9. 在 中， ∠ ，且 ，则 ( )
∘
( A  )      = 3（,  B）  = 2,    = 120（C）     = 2     （D）    ⋅     =
1 2
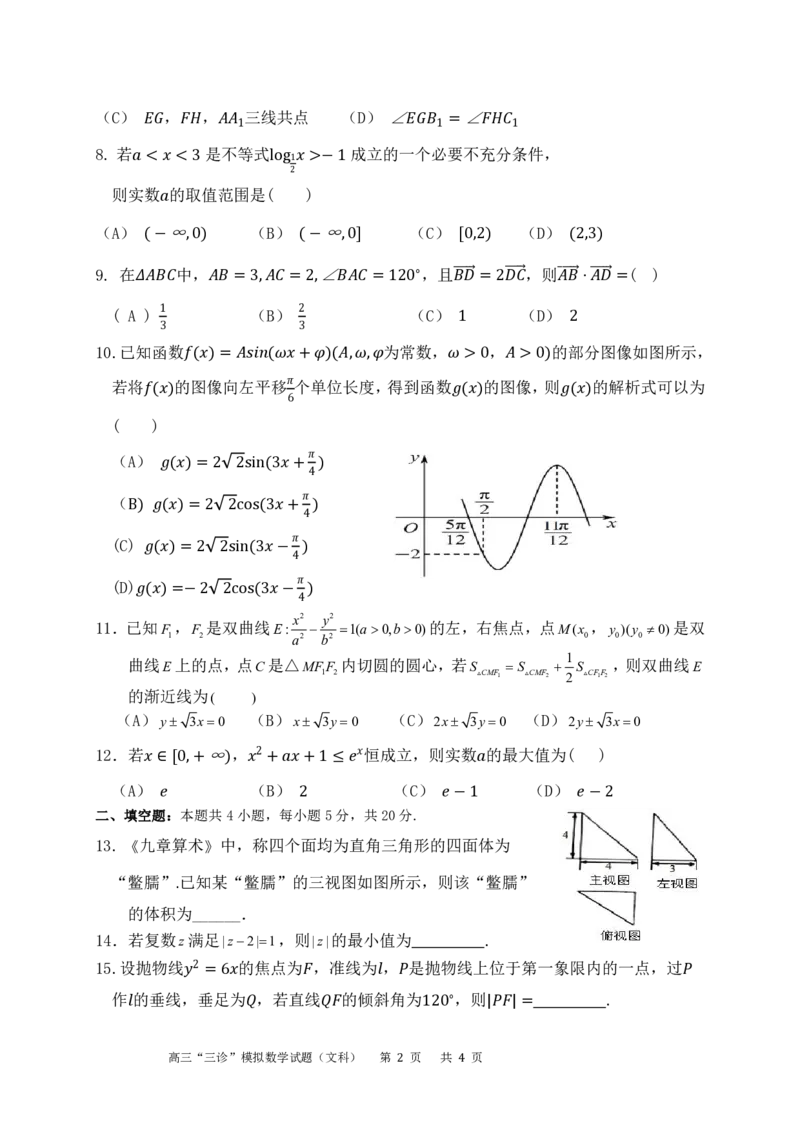
10.已知函3数 3 为常数， 1 ， 的部2 分图像如图所示，
若将 的  图(  像) =向  左   平  (移   个+单  )位(  长,  度,  ，得到函数  > 0的图  像>，0则) 的解析式可以为

(  )(  ) 6  (  )  (  )
（A）

（
(  ) = 2 2sin(3  +4)

(C
B
)
)  (  ) = 2 2cos(3  +4)

(D)
(  ) = 2 2sin(3  −4)

11．已  知(  ) F =，− F 2是双2c曲os(线3  E − : x4 2 )  y2 1(a0,b0)的左，右焦点，点 M(x ， y )(y 0) 是双
1 2 a2 b2 0 0 0
1
曲线E上的点，点 C 是△ MFF 内切圆的圆心，若 S S  S ，则双曲线E
1 2 CMF1 CMF2 2 CF1F2
的渐近线为
( )
（A） y 3x0 （B） x 3y0 （C） 2x 3y0 （D） 2y 3x0
12．若 ∞， 恒成立，则实数 的最大值为( )
2 
（A）  ∈ [0,+ )  （+B）   +1 ≤  （C）  （D）
二、填空题：本题共4小题，每小题5分，共20分.
2  −1  −2
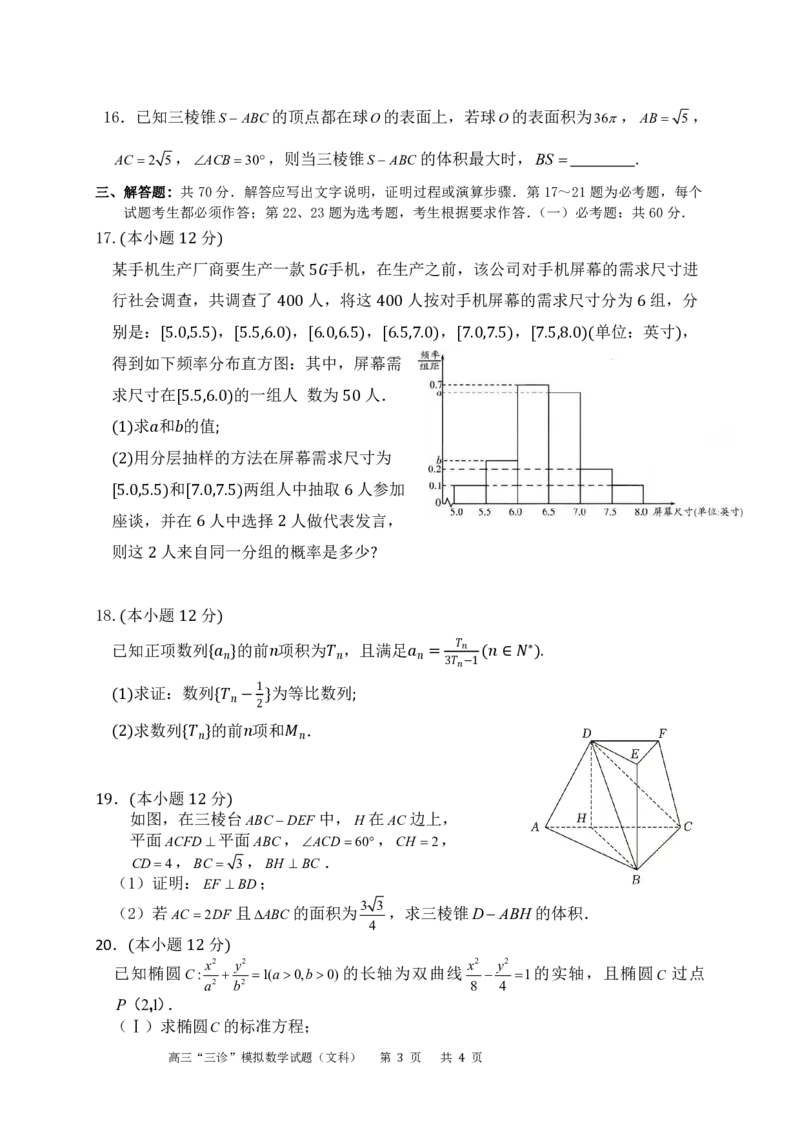
13.《九章算术》中，称四个面均为直角三角形的四面体为
“鳖臑”已知某“鳖臑”的三视图如图所示，则该“鳖臑”
的体积为______．
.
14．若复数z满足|z2|1，则|z|的最小值为 .
15.设抛物线 的焦点为 ，准线为 ， 是抛物线上位于第一象限内的一点，过
2
作 的垂线，垂足为 ，若直线 的倾斜角为 ，则 .
= 6     
∘
120 |   | =
高三“三诊”模拟数学试题（文科） 第 页 共 页
2 4
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#}16．已知三棱锥 S  ABC 的顶点都在球 O 的表面上，若球 O 的表面积为 36， AB 5 ，
AC 2 5 ，ACB30，则当三棱锥 S  ABC 的体积最大时，BS  .
三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每个
试题考生都必须作答；第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．
17. 本小题 分
某手机生产厂商要生产一款 手机，在生产之前，该公司对手机屏幕的需求尺寸进
( 12 )
行社会调查，共调查了 人，将这 人按对手机屏幕的需求尺寸分为 组，分
5 
别是： ， ， ， ， ， 单位：英寸 ，
400 400 6
得到如下频率分布直方图：其中，屏幕需
[5.0,5.5) [5.5,6.0) [6.0,6.5) [6.5,7.0) [7.0,7.5) [7.5,8.0)( )
求尺寸在 的一组人 数为 人．
求 和 的值
[5.5,6.0) 50
用分层抽样的方法在屏幕需求尺寸为
(1)   ;
和 两组人中抽取 人参加
(2)
座谈，并在 人中选择 人做代表发言，
[5.0,5.5) [7.0,7.5) 6
则这 人来自同一分组的概率是多少
6 2
2 ?
18. 本小题 分
已(知正项数12列 ) 的前 项积为 ，且满足
∗
{   }      = 3   −1(  ∈  ).
求证：数列 为等比数列
1
(1)求数列 的{  前  −项2}和 ． ;
(2) {   }   
． 本小题 分
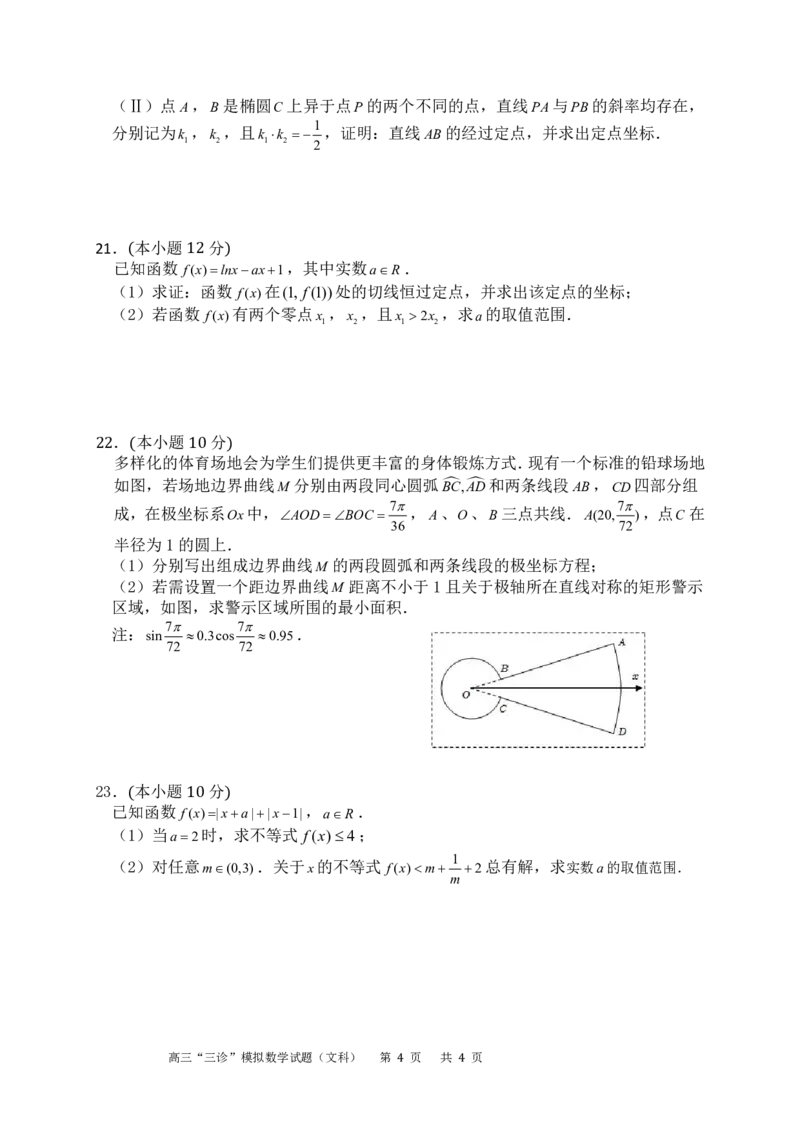
如图，在三棱台 ABCDEF 中， H 在 AC 边上，
19 ( 12 )
平面 ACFD平面 ABC ，ACD60， CH 2 ，
CD4 ， BC  3 ， BH  BC ．
（1）证明： EF BD ；
3 3
（2）若 AC 2DF 且ABC 的面积为 ，求三棱锥D ABH 的体积．
4
20． 本小题 分
x2 y2 x2 y2
已 ( 知椭圆C 12 :  ) 1(a0,b0)的长轴为双曲线  1的实轴，且椭圆 C 过点
a2 b2 8 4
P（2，1）．
（Ⅰ）求椭圆 的标准方程；
C
高三“三诊”模拟数学试题（文科） 第 页 共 页
3 4
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#}（Ⅱ）点 ， 是椭圆 上异于点 的两个不同的点，直线 与 的斜率均存在，
A B C P PA PB
1
分别记为 k ， k ，且 k k  ，证明：直线AB的经过定点，并求出定点坐标．
1 2 1 2 2
21． 本小题 分
已知函数 f(x)lnxax1 ，其中实数 aR ．
( 12 )
（1）求证：函数
f(x)
在(1, f(1))处的切线恒过定点，并求出该定点的坐标；
（2）若函数 f(x) 有两个零点 x ， x ，且 x 2x ，求 a 的取值范围．
1 2 1 2
． 本小题 分
多样化的体育场地会为学生们提供更丰富的身体锻炼方式．现有一个标准的铅球场地
22 ( 10 )
如图，若场地边界曲线
M
分别由两段同心圆弧BC,AD和两条线段
AB
，
CD
四部分组
7 7
成，在极坐标系 Ox 中，AODBOC  ， A 、 O 、 B 三点共线． A(20, ) ，点 C 在
36 72
半径为1的圆上．
（1）分别写出组成边界曲线 的两段圆弧和两条线段的极坐标方程；
M
（2）若需设置一个距边界曲线M 距离不小于1且关于极轴所在直线对称的矩形警示
区域，如图，求警示区域所围的最小面积．
7 7
注： sin 0.3cos 0.95 ．
72 72
23． 本小题 分
已知函数 f(x)|xa||x1| ， aR ．
( 10 )
（1）当 a2 时，求不等式 f(x)4；
1
（2）对任意 m(0,3) ．关于 x 的不等式 f(x)m 2 总有解，求实数a的取值范围．
m
高三“三诊”模拟数学试题（文科） 第 页 共 页
4 4
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#}高三三诊模拟考试数文科答案
一、选择题：1---5: CCDBC 6---10: ADBCA 11---12: AD
二、 填空题：13. 8 14. 1 15. 6 16. 30
三、解答题：
17.解：（1）因为屏幕需求尺寸在 的一组人数为 人，
[5.5,6.0) 50
所以其频率为 ．又因为组距为 ，所以 ．
50 0.125
又因为 400=0.125 0.5 ，  所=以0.5 =0.2，5
即 0.1，+0.25+0．.7+..  .+..0...2.+..0...1..×.60.分5=1  =0.65
因=为0屏.65幕需  求=尺0.2寸5为 人数为： ，
(屏2)幕需求尺寸为 [人5.0数,5为.5) 0.1×0.5×，400=20
若要用分层抽样的[7.方0,7法.5抽) 取 人0，.2×0.5×400=40
所以要在 组中抽 人6，设为 ， ；要在 组中抽 人，设为 ， ， ， ，
因此样本空[5.间0,5.5) 2   [7.0,7.5) 4    
， ，  ={  ，,  ,  ,，  ,  ,  ，,  ,  ,，  ,  ,
,  ，  ,  ，  ,  ，  ,  ，共  ,  个  基,  本事件，
而  ,这  人  来,  自同  一,  分组为  ,事  件} ，15
2  ，共 个基本事件，
={  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  } 7
所以这 人来自同一分组的概率 ．.................12分
7
2   =15
18.解： 证明：因为 ，且 ，所以 ，

(1)   =3   −1   =   −1(  ≥2)   −1 =3   −1
因为 ，所以 ，所以得 ，则 ，
1 1 1
>0   >0 3   −1=   −1   −2=3(   −1−2)
因为当 时， ，得 ，所以 ．
1 2 1 1
=1  1 =3  1−1  1 =3  1−2=6
所以数列 是首项为 ，公比为 的等比数列．...........6分
1 1 1
{   −2} 6 3
由 知： ，即 ．
1 1 1  −1 1 1  1
(2) (1)   −2=6⋅(3)   =2⋅(3) +2
所以 ．
1 1 1 2 1   1 1  
=  1+  2+⋯+   =2[3+ . ( .3. ) .. + .. ⋯ ... + . ( ..3. ) .. + ..2. = ..4. [ 1 1 2 −分(3) ]+2
19．
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#}证明：（1）ACD60，CH 2，CD4，
1 CD2 CH2 DH2
由余弦定理得cosACD  ，解得DH 2 3，
2 2CDCH
所以CD2 CH2 DH2，所以DH  AC，

又因为平面ACFD平面ABC，平面ACFD 平面ABC  AC ，
DH 平面ACFD，所以DH 平面ABC，
因为BC平面ABC，所以DH BC，
又因为BH BC，BHDH H ，BH 平面BDH ，DH 平面BDH ，
所以BC 平面BDH ，因为DB平面BDH ，所以BC DB，
又因为BC//EF ，所以EF DB； ..................................................6分
（2）在RtBHC中，CH 2，BC  3，BH BC，
BC 3
所以BC CH2 BC2 1，cosACB  ，所以ACB30，
CH 2
3 3 3 3 1
因为S  ，又S   ACBCsin30，
ABC 4 ABC 4 2
解得AC 3，则AC 3 AH HC，所以AH 1
1 1 1 3 1
V  S .DH   1 2 3  .................12分
DABH
3
ABH
3 2 2 2
2a4 2,
 a2 2
20．解：（1）由题意，知
4 1
解得 ，
  1, b2 2
a2 b2
x2 y2
所以椭圆C的标准方程为  1．......................5分
8 2
（2）①当直线AB的斜率存在时，设其方程为ykxt，A(x ，y )，B(x ，y )，
1 1 2 2
x2 4y2 8
联立 ，得(4k2 1)x2 8ktx4t2 80，
ykxt
 8kt  2t
x x  y  y 
  1 2 4k2 1   1 2 4k2 1
由韦达定理得 ，所以 ，

4t2 8

t2 8k2
xx  y y 
 1 2 4k2 1  1 2 4k2 1
因为
y 1 y 1 y y (y  y )1 t2 2t4k2 1 (t1)2 4k2 t12k 1
k k  1  2  1 2 1 2    
1 2 x 2 x 2 xx 2(x x )4 4t216kt16k24 4(t2k)24 4(t2k1) 2
1 2 1 2 1 2
，
2k1 2k1
所以3t2k 10，即t  ，所以直线AB的方程为ykx ，
3 3
 2
x
3x20   3 2 1
即(3x2)k(3y1)0，由 ，得 ，故直线AB恒过点M( , )；
3y10  y 1 3 3
 3
②当直线AB的斜率不存在时，设A(x ，y )，则B(x ，y )，
0 0 0 0
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#}y 1 y 1 1y2 x 2 1 2
所以k k  0  0  0  0  ，解得x  ，
1 2 x 2 x 2 (x 2)2 4(x 2) 2 0 3
0 0 0 0
2 1
所以此时直线AB也过点M( , )........................................................12分
3 3
1
21．解：（1）证明：因为 f(x)lnxax1，所以 f(x) a，所以 f(l)1a，又 f(l)la，
x
所以切线方程为y(la)(1a)(x1)，即 y(1a)x，
则当x0时y0，所以切线恒过定点(0,0)；...................................,5分
1 1ax
（2）解：因为 f(x)lnxax1的定义域为(0,)，所以 f(x) a ，
x x
当a„0时， f(x)0恒成立，所以 f(x)在(0,)上单调递增，
故 f(x)不可能有两个零点，故舍去；
1 1
当a0肘，令 f(x)0，解得0 x ，令 f(x)0，解得x ，
a a
1 1
所以 f(x)在(0, )上单调递增，在( ，)上单调递减，
a a
1 1 1 1
所以 f(x)  f( )ln ，要使 f(x)有两个零点，则 f(x)  f( )ln 0，解得0al ，
max a a max a a
1 1 1 a 4 4 4 2 4 2
又 f( )ln a 1 0， f( )ln  1  11 0，
e e e e a2 a2 a a a a
1 1 1 4
所以当0a1时， f(x)在( ， )和( ， )上各有一个零点x ，x 且x x ，
e a a a2 2 1 1 2
lnx ax 10
所以 1 1 ，由 f(x)单调性知，当x(x ，x)时， f(x)0，当x(x ，)时
lnx ax 10 2 1 1
2 2
f(x)0，
因为x 2x  x ，所以 f(2x )0，即ln(2x )a2x 1lnx ax l，
2 2 1 2 2 2 2 2
2
所以ax ln2，而ax lnx 1ln2，所以0x  ，
2 2 2 2 e
lnx 1 lnx1 2
所以a 2 ，令h(x) ，x(0, )，
x x e
2
1lnx1 lnx 2
则h(x)  0，所以h(x)在(0, )上单调递增，
x2 x2 e
2 ln2 eln2 eln2
所以h(x)h( )  ，所以a(0, )．......................................12分
e 2 2 2
e

22．解：（ ）由题意，以 为原点，AD的垂直平分线为极轴建立极坐标系，
线段AB: 1  1 AOD 7O 120，
2 72
7 137
线段CD:2  120，
72 72
弧 ：
7 137
1(  )
BC 72 72
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#} 7 137 
弧AD:200 , 2 ； 分
 72 72 
（ ）解：求警示区域最小值即让内界线到 .....距.....离.....恰.....好.....为........，....5设矩形长为 ，
则2l 1112023（包括弧长半径､圆半M径､两边距距离1）， l
7 7
矩形宽为 ，则d 20sin 6,d 20sin 6，d d d 1114，
1 72 2 72 1 2
所以S  d ld 1423332 分
................................................................10
23．解：（1）由已知，不等式 f(x)4即为 x2  x1 4，
5 3
解得  x
2 2
5 3
故不等式的解集为[ ， ]．...................................................5分
2 2
1 1
（2）对任意m(0,3)．关于x的不等式 f(x)m 2总有解 f(x) (m 2) ，
m min m min
1 1 1
而ym 2 2 m 24，当且仅当m ，即m1时取得最小值．
m m m
又 f(x) (xa)(x1)  a1（当且仅当(xa)(x1)„0时取等号），
故只需|a1|4，解得5a3，即实数a的取值范围为(5,3)．......................12分
{#{QQABBYIUggCgQpBAARhCUQWACgEQkACACCoGBAAMMAABiQNABAA=}#}