文档内容
漯河市 2023-2024 学年下学期期末质量监测
高一数学
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项符合题目要求.
1. 已知集合 ,则 ( )
A. B. C. D.
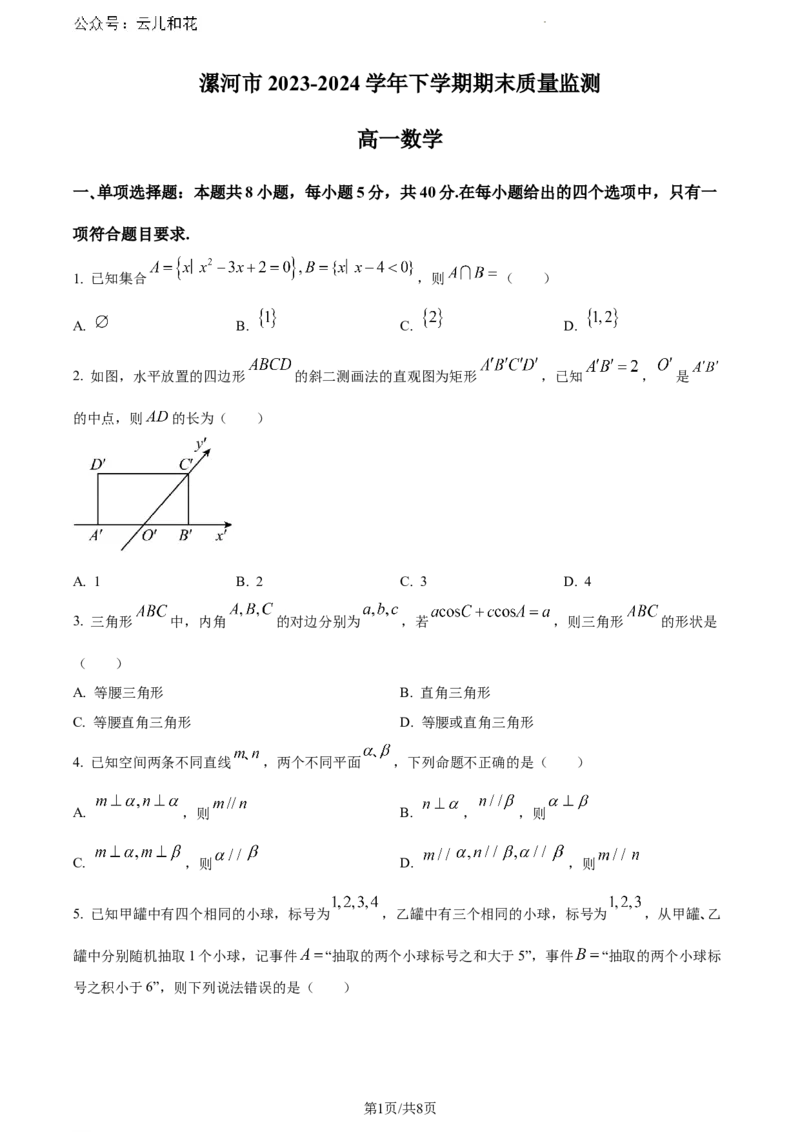
2. 如图,水平放置的四边形 的斜二测画法的直观图为矩形 ,已知 , 是
的中点,则 的长为( )
A. 1 B. 2 C. 3 D. 4
3. 三角形 中,内角 的对边分别为 ,若 ,则三角形 的形状是
( )
A. 等腰三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰或直角三角形
4. 已知空间两条不同直线 ,两个不同平面 ,下列命题不正确的是( )
A. ,则 B. , ,则
C. ,则 D. ,则
5. 已知甲罐中有四个相同的小球,标号为 ,乙罐中有三个相同的小球,标号为 ,从甲罐、乙
罐中分别随机抽取1个小球,记事件 “抽取的两个小球标号之和大于5”,事件 “抽取的两个小球标
号之积小于6”,则下列说法错误的是( )
第1页/共8页
学科网(北京)股份有限公司A. 事件 发生的概率为 B. 事件 相互独立
C. 事件 是互斥事件 D. 事件 发生的概率为
6. 已知向量 , 满足 , ,且 与 夹角的余弦值为 ,则 ( )
A. B. C. D.
7. 函数 ,则“ ”是“函数 在 上存在零点”的( )
A. 充分不必要条件 B. 充分必要条件
.
C 必要不充分条件 D. 既不充分也不必要条件
8. 已知O为 的外心,且 .若向量 在向量 上的投影向量为 ,
则 的值为( )
.
A 1 B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的是( )
A. 复数 的虚部为
B. 复数 的共轭复数
C. 若角 的终边经过点 ,则
D. 函数 的一个对称中心是
第2页/共8页
学科网(北京)股份有限公司10. 在 中, , , 所对的边分别是 , , , , ,则( )
A. 若 ,则角 有一个解
B. 若 ,则 边上的高为
C. 的周长不可能为
D. 若 为锐角三角形,则 面积的最值范围为
11. 已知正方体 的棱长为3,棱 的中点分别为 ,点 在底面正方形
内(含边界),且平面 ∥平面 ,则下列说法正确的是( )
A. 若存 在实数 使得 ,则
B. 若 ,则 ∥平面
C. 三棱锥 体积的最大值为
D. 二面角 的正切值为
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知平面向量 ,若向量 与 共线,则 __________.
13. 某校有高一学生1000人,其中男生600人,女生400人,为了获取学生身高信息,采用男、女按比例
分配分层抽样的方法抽取样本 50人,并观测样本的指标值(单位: ),计算得男生样本的均值为
170,方差为20,女生样本的均值为 160,方差为30,据此估计该校高一年级学生身高的总体方差为
____________.
的
14. 在侧棱长为4 正三棱锥 中,点 为线段 上一点,且 ,则该正三棱锥
的外接球体积为__________.
第3页/共8页
学科网(北京)股份有限公司四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 设复数 (其中 ), .
(1)若 是实数,求 的值;
(2)若 是纯虚数,求 .
16. 已知三角形 的内角 所对的边分别为 ,若 ,且 .
(1)若 ,求 ;
(2)点 在边 上且 平分 ,若 ,求三角形 的周长.
17. 俄罗斯与乌克兰的军事冲突导致石油、天然气价格飙升.燃油价格问题是人们关心的热点问题,某网站
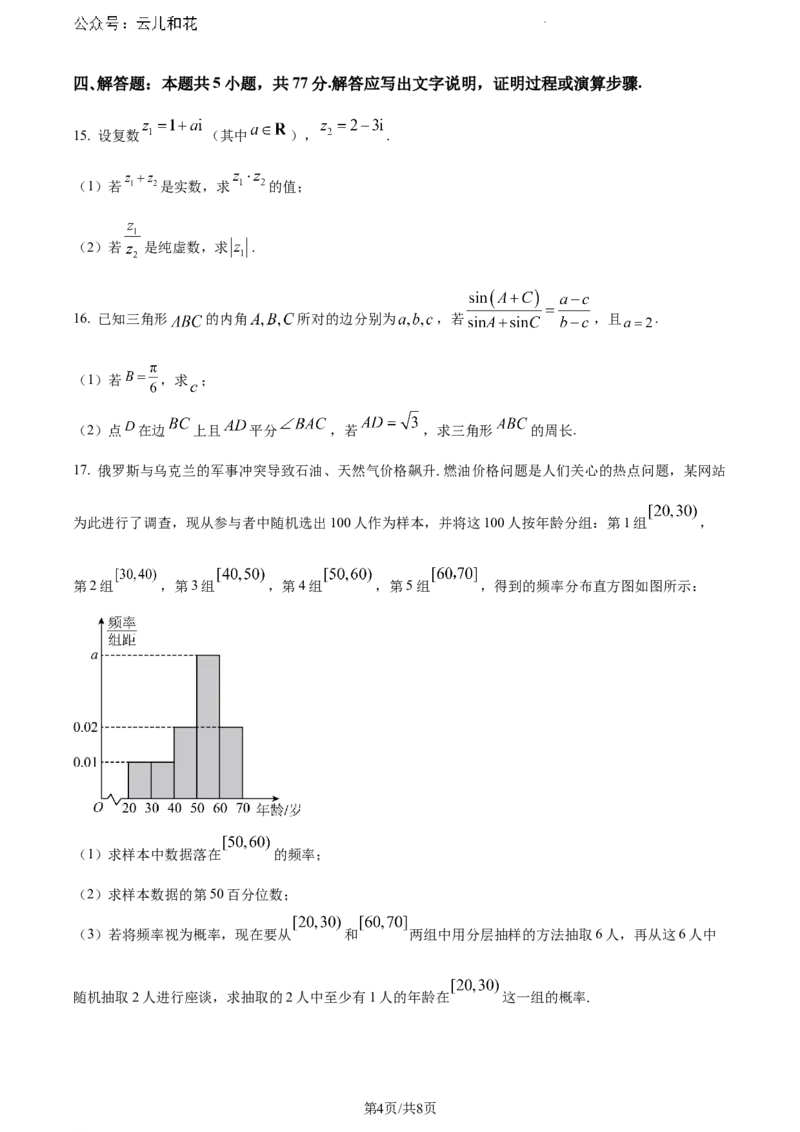
为此进行了调查,现从参与者中随机选出100人作为样本,并将这100人按年龄分组:第1组 ,
第2组 ,第3组 ,第4组 ,第5组 ,得到的频率分布直方图如图所示:
(1)求样本中数据落在 的频率;
(2)求样本数据的第50百分位数;
(3)若将频率视为概率,现在要从 和 两组中用分层抽样的方法抽取6人,再从这6人中
随机抽取2人进行座谈,求抽取的2人中至少有1人的年龄在 这一组的概率.
第4页/共8页
学科网(北京)股份有限公司18. 在四棱锥 中,平面 平面 ,E为 边上一点, 为 中点,
.
的
(1)求四棱锥 体积;
(2)证明: 平面 ;
(3)证明:平面 平面 .
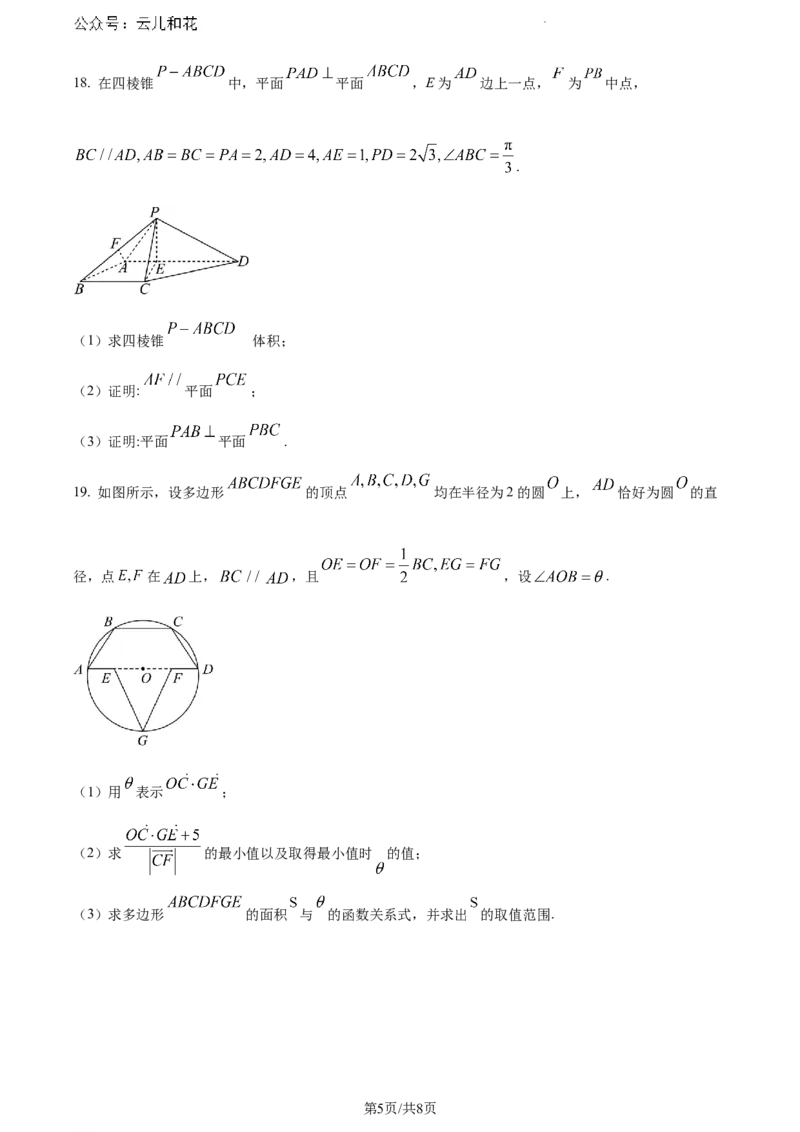
19. 如图所示,设多边形 的顶点 均在半径为2的圆 上, 恰好为圆 的直
径,点 在 上, ,且 ,设 .
(1)用 表示 ;
(2)求 的最小值以及取得最小值时 的值;
(3)求多边形 的面积 与 的函数关系式,并求出 的取值范围.
第5页/共8页
学科网(北京)股份有限公司漯河市 2023-2024 学年下学期期末质量监测
高一数学
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项符合题目要求.
【1题答案】
【答案】D
【2题答案】
【答案】C
【3题答案】
【答案】A
【4题答案】
【答案】D
【5题答案】
【答案】B
【6题答案】
【答案】A
【7题答案】
【答案】C
【8题答案】
【答案】D
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】BCD
【10题答案】
【答案】BD
【11题答案】
【答案】ABD
三、填空题:本题共3小题,每小题5分,共15分.
第6页/共8页
学科网(北京)股份有限公司【12题答案】
【答案】 ##
【13题答案】
【答案】48
【14题答案】
【答案】
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
【15题答案】
【答案】(1)
(2)
【16题答案】
【答案】(1)
(2)6
【17题答案】
【答案】(1)0.4 (2)52.5
(3)
【18题答案】
【答案】(1)3 (2)证明见解析
(3)证明见解析
【19题答案】
【答案】(1)
(2)最小值4,
第7页/共8页
学科网(北京)股份有限公司(3) ,
第8页/共8页
学科网(北京)股份有限公司