文档内容
绵阳南山中学高2021级高三下期高考仿真演练1试题
理科数学
命题人:曾皓 审题人:何宗福
一、选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,
只有一项是符合题目要求的。
U={x|log x>0} A={x|x2 −3x+2<0} C A=
1.已知全集 2 ,集合 ,则 U ( )
(−∞,1)∪(2,+∞) [2,+∞) (2,+∞) (−∞,1]∪[2,+∞)
A. B. C. D.
z
z=
z i5
2.设复数 的共轭复数为 ,且满足 ,则 可以是( )
A. 1+i B. 1−i C.i D.−i
f(x)=(ex −ae−x )cosx
3.已知函数 是奇函数,则实数a=( )
A. B. C. D.
4.在区间 [−2,2] 上随机取一个实数a,使 f(x)=ax−sinx 在R上单调递增的概率是
( )
1 2 3 1
3 3 4 4
A. B. C. D.
√3
5.已知某几何体的三视图如图所示,该几何体最长的棱为 ,
则该几何体的体积为( )
1 2
俯视图
3 3
A. B.
1 1
6 2
C. D.
6.如图,在棱长为2的正方体
ABCD−A
1
B
1
C
1
D
1中,
O
1是正方体上底面的中心,P是
B C PO A BC
1 1的中点,则 1与平面 1 1所成角的正切值为( )
1 √2
2 2
A. B.
√2
C. D.2
第 1 页 共 6 页
学科网(北京)股份有限公司第 1 页 共 6 页
7.将2名医生和甲、乙、丙、丁4名护士分成2个小组,分别安排到两个社区参加义诊活
动,每个社区有1名医生和2名护士,其中甲乙不在同一小组,则不同的分配方法有(
)种.
A.6 B.8 C.10 D.12
1
f(x)=√3sinxcosx−cos2x+
2
8.关于函数 ,有下列命题:
( π )
,0
①
f (x)
的最小正周期为π; ②函数
f (x)
的图象关于
12
对称;
[π π] 5π
,
f (x) 3 2 f (x) 12
③ 在区间 上单调递增; ④将函数 的图象向右平移 个单位长度
y=sin2x
后所得到的图象与函数 的图象重合.
其中正确的为( )
A.①② B.①③ C.①②③ D.①②④
9.已知函数 有两个不同的
根,分别是 ( )
B.3 C.6 D.9
10.过双曲线 的左焦点 的直线 (斜率为正)交双曲线于
两点,满足 ,设 为 的中点,则直线 ( 为坐标原点)斜率的
最小值是( )
√3 √5
A. B. C. D.
1
a =1,a −a =
{a } 1 n+1 n a +a [x]
11.已知数列 n 的各项均为正数, n+1 n,若 表示不超过x的
第 2 页 共 6 页
学科网(北京)股份有限公司第 2 页 共 6 页
[a ]+[a ]+⋯+[a ]=
最大整数,则 1 2 100 ( )
A.615 B.620 C.625 D.630
12.若函数
f(x)=log
a
x+log
(1+a)
x
在
(0,+∞)
上单调递增,则a不可能的取值为(
)
1 ln2 √e
e 2 ln1.6 2
A. B. C. D.
二、填空题:本大题共4小题,每小题5分,共20分。
{x 2 {x y 0
≤ ¿ + ≥ ¿¿¿¿
13.若x,y满足约束条件 则 z=x+2 y 的最小值为 .
⃗a,⃗b 2|⃗a|=| ⃗b| ⃗a⊥(⃗a− ⃗b), ⃗a,⃗b
14.已知非零向量 满足 ,且 则 的夹角大小为 .
1 n
( )
S =−15 +t
{a } S n 2 a a ⋯a
15.已知等比数列 n 的前n项和为 n,若 ,则 1 2 n取最大值时,
n的值为 .
16.已知圆 C:x2 +(y−3) 2 =1 ,点P在抛物线 T:x2 =4 y 上运动,过点P作圆 C 的切线
l ,l A,B PACB
1 2,切点分别为 ,则四边形 面积最小值为 .
三、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
(一)必考题:共60分.
17.数学来源于生活,当然也服务于生活。某学校兴趣小组针对“当地某一零售超市夏天
如何配备冷饮”的问题,做了一系列研究。经研究发现,“冷饮的需求量(单位:杯)”
°C
与“当天的气温(单位: )”线性相关。根据统计,小组随机抽取了该超市6天销量情
况与当天的气温,对应关系如下表:
°C 17 19 23 29 33 35
气温x( )
销量y(杯) 78 87 96 110 13 149
4
¿^=3.6x+m
(1)经过计算,得到当天的气温x与销量y满足回归方程 y ¿.若今天的气温为31
°C
,则该超市可以配备多少杯冷饮?
第 3 页 共 6 页
学科网(北京)股份有限公司第 3 页 共 6 页
(2)为了进一步详细研究这种变化规律,该小组又从这6天中随机选取3天,记X 为销量不
低于110杯的天数,求X 的分布列和数学期望.
ΔABC AD=√5
18.已知在 中,D为BC边的中点,且 .
√5
cos∠ADC=
(1)若 ΔABC 的面积为2, 5 ,求B;
(2)若
AB2 +AC2 =18
,求
ΔABC
的周长的最大值.
19.在四棱锥 中,底面 为平行四边形, , ,
, .
,
(1)证明:平面
PAC⊥¿¿平面PBD;
PE
=λ(0<λ<1)
(2) E是侧棱 PB 上一点,记 PB ,是否存在实数
λ ADE ABCD 60∘ λ
,使平面 与平面 所成的二面角为 ?若存在,求出 的值;若不存在,
请说明理由.
f(x)=2sinx+ln(x+1)−ax
20.已知函数 .
( π)
0,
(1)当
a=2
时,求函数
f (x)
在区间
2
上零点的个数;
(2)若 x≥0 时,不等式 f (x)≤0 恒成立,求实数a的取值范围.
21.已知椭圆 组合成的曲线
如图1所示,根据图形特点,称曲线 为“猫眼曲线”.特别地,若两个椭圆离心率相等,
则称为“优美猫眼曲线”.
第 4 页 共 6 页
学科网(北京)股份有限公司第 4 页 共 6 页
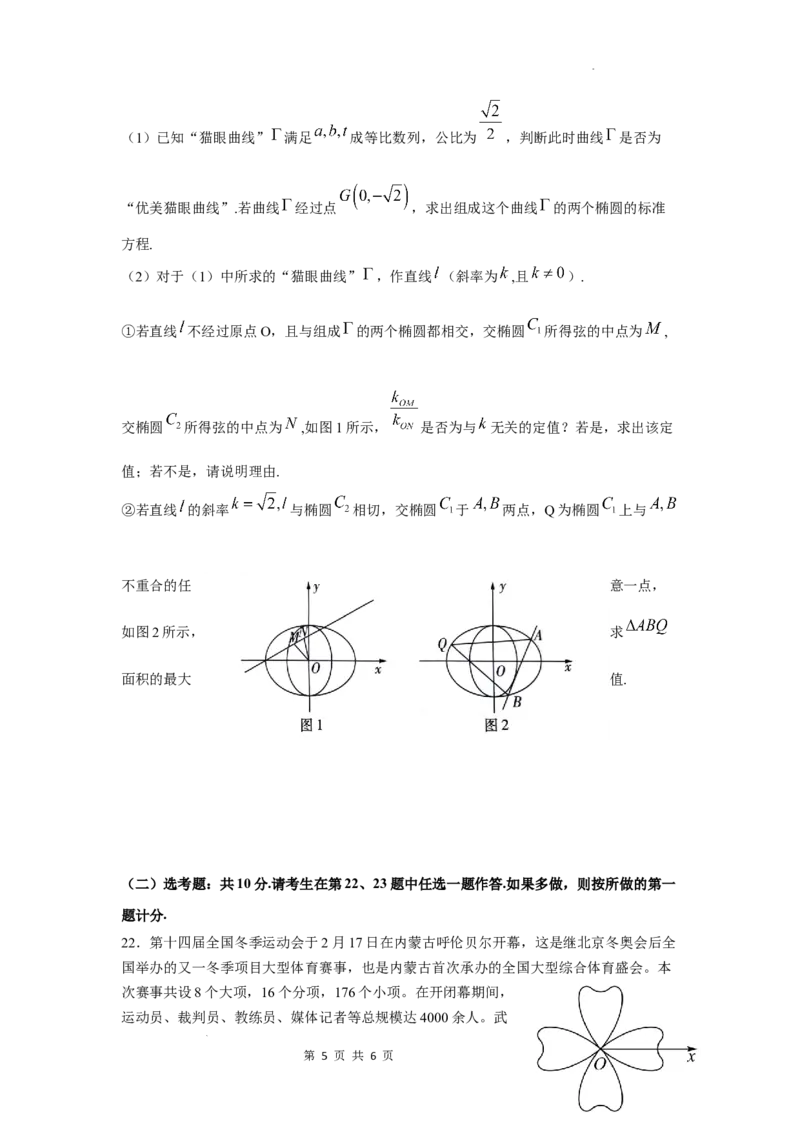
(1)已知“猫眼曲线” 满足 成等比数列,公比为 ,判断此时曲线 是否为
“优美猫眼曲线”.若曲线 经过点 ,求出组成这个曲线 的两个椭圆的标准
方程.
(2)对于(1)中所求的“猫眼曲线” ,作直线 (斜率为 ,且 ).
①若直线 不经过原点O,且与组成 的两个椭圆都相交,交椭圆 所得弦的中点为 ,
交椭圆 所得弦的中点为 ,如图1所示, 是否为与 无关的定值?若是,求出该定
值;若不是,请说明理由.
②若直线 的斜率 与椭圆 相切,交椭圆 于 两点,Q为椭圆 上与
不重合的任 意一点,
如图2所示, 求
面积的最大 值.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一
题计分.
22.第十四届全国冬季运动会于2月17日在内蒙古呼伦贝尔开幕,这是继北京冬奥会后全
国举办的又一冬季项目大型体育赛事,也是内蒙古首次承办的全国大型综合体育盛会。本
次赛事共设8个大项,16个分项,176个小项。在开闭幕期间,
运动员、裁判员、教练员、媒体记者等总规模达4000余人。武
第 5 页 共 6 页
学科网(北京)股份有限公司第 5 页 共 6 页
大靖、任子威等明星运动员也纷纷亮相。某高中体育爱好者打算借四叶草具有幸福幸运的
象征意义,准备设计一枚四叶草徽章以作纪念。如图,在极坐标系ox中,方程
ρ=2sin2θ C
表示的图形为“四叶草”对应的曲线 .
π
θ∈[0, ]
C 2 C
(1) 当 的 时;求以极点为圆心的单位圆与 的交点的极坐标;
π
∠AOB=
|OA|+|OB|
(2) 设A和B是 C 上的两点,且 6 ,求 的最大值.
f(x)=|x|+|1−x|
23.已知函数 的最小值是m.
(1)求m的值;
1 2 1 2 25
( ) ( )
a+ + b+ ≥
a>0,b>0,a+b=m a b 2
(2)若 ,证明: .
第 6 页 共 6 页
学科网(北京)股份有限公司