文档内容
第4单元 指数函数与对数函数(巩固篇)
基础知识讲解
一.指数函数的定义、解析式、定义域和值域
【基础知识】
1、指数函数的定义:
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是
R,值域是(0,+∞).
2、指数函数的解析式:
y=ax(a>0,且a≠1)
【技巧方法】
①因为a>0,x是任意一个实数时,ax是一个确定的实数,所以函数的定义域为实数集
R.
②规定底数a大于零且不等于1的理由:
如果a=0,当x>0时,ax恒等于0;当x≤0时,ax无意义;
如果a<0,比如y=(﹣4)x,这时对于x= ,x= 在实数范围内函数值不存在.
如果a=1,y=1x=1是一个常量,对它就没有研究的必要,
为了避免上述各种情况,所以规定a>0且a≠1.
二.指数函数的图象与性质
【基础知识】
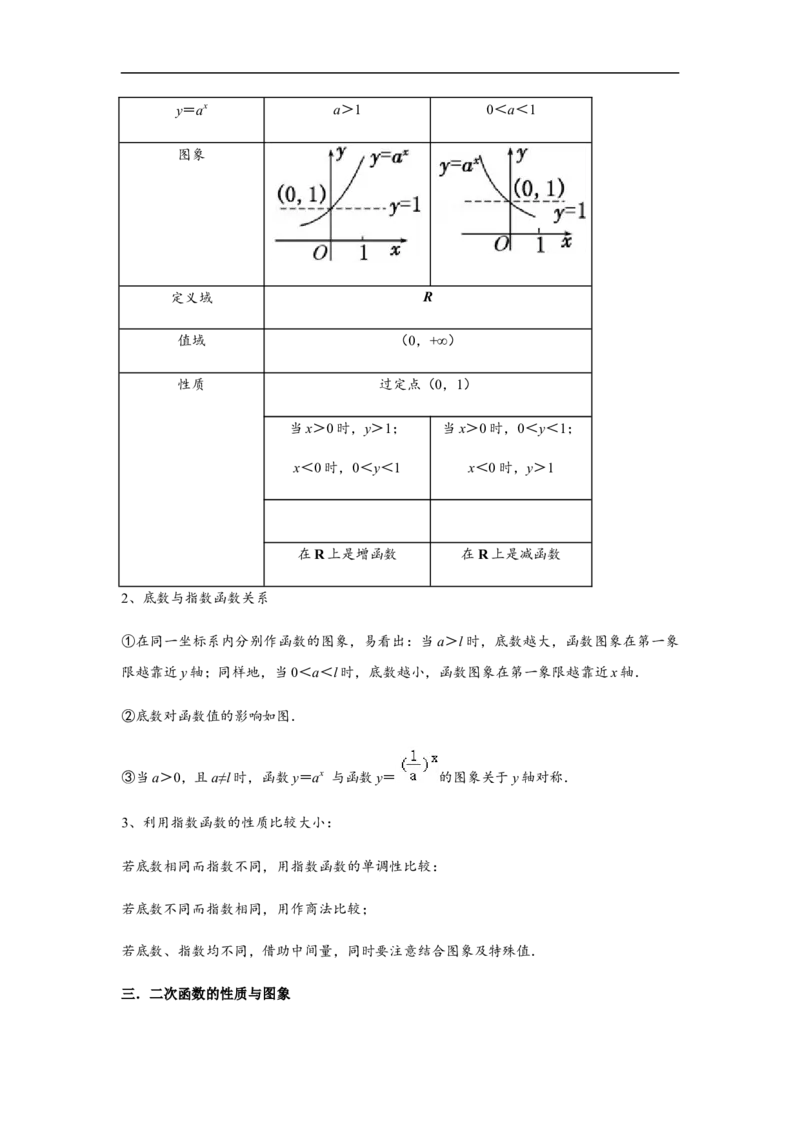
1、指数函数y=ax(a>0,且a≠1)的图象和性质:y=ax a>1 0<a<1
图象
定义域 R
值域 (0,+∞)
性质 过定点(0,1)
当x>0时,y>1; 当x>0时,0<y<1;
x<0时,0<y<1 x<0时,y>1
在R上是增函数 在R上是减函数
2、底数与指数函数关系
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象
限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.
③当a>0,且a≠l时,函数y=ax 与函数y= 的图象关于y轴对称.
3、利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值.
三.二次函数的性质与图象【二次函数】
二次函数相对于一次函数而言,顾名思义就知道它的次数为二次,且仅有一个自变量,
因变量随着自变量的变化而变化.它的一般表达式为:y=ax2+bx+c(a≠0)
【二次函数的性质】
二次函数是一个很重要的知识点,不管在前面的选择题填空题还是解析几何里面,或
是代数综合体都有可能出题,其性质主要有初中学的开口方向、对称性、最值、几个根的
判定、韦达定理以及高中学的抛物线的焦点、准线和曲线的平移.
这里面略谈一下他的一些性质.
①开口、对称轴、最值与x轴交点个数,当a>0(<0)时,图象开口向上(向下);对称
轴x=﹣ ;最值为:f(﹣ );判别式△=b2﹣4ac,当△=0时,函数与x轴只有一
个交点;△>0时,与x轴有两个交点;当△<0时无交点.
②根与系数的关系.若△≥0,且x 、x 为方程y=ax2+bx+c的两根,则有x +x =﹣ ,
1 2 1 2
x •x = ;
1 2
③二次函数其实也就是抛物线,所以x2=2py的焦点为(0, ),准线方程为y=﹣ ,
含义为抛物线上的点到到焦点的距离等于到准线的距离.
④平移:当y=a(x+b)2+c向右平移一个单位时,函数变成y=a(x﹣1+b)2+c;
四.指数型复合函数的性质及应用
【基础知识】
指数型复合函数性质及应用:
指数型复合函数的两个基本类型:y=f(ax)与y=af(x)
复合函数的单调性,根据“同增异减”的原则处理U=g(x) y=au y=ag(x)
增 增 增
减 减 增
增 减 减
减 增 减.
五.指数函数的单调性与特殊点
【基础知识】
1、指数函数单调性的讨论,一般会以复合函数的形式出现,所以要分开讨论,首先讨论 a
的取值范围即a>1,0<a<1的情况.再讨论g(x)的增减,然后遵循同增、同减即为增,
一减一增即为减的原则进行判断.
2、同增同减的规律:
(1)y=ax 如果a>1,则函数单调递增;
(2)如果0<a<1,则函数单调递减.
3、复合函数的单调性:
(1)复合函数为两个增函数复合:那么随着自变量X的增大,Y值也在不断的增大;
(2)复合函数为两个减函数的复合:那么随着内层函数自变量X的增大,内层函数的Y值
就在不断的减小,而内层函数的Y值就是整个复合函数的自变量X.因此,即当内层函数
自变量X的增大时,内层函数的Y值就在不断的减小,即整个复合函数的自变量X不断减
小,又因为外层函数也为减函数,所以整个复合函数的Y值就在增大.因此可得“同增”
若复合函数为一增一减两个函数复合:内层函数为增函数,则若随着内层函数自变量X的
增大,内层函数的Y值也在不断的增大,即整个复合函数的自变量X不断增大,又因为外
层函数为减函数,所以整个复合函数的Y值就在减小.反之亦然,因此可得“异减”.
六.函数零点的判定定理
【基础知识】1、函数零点存在性定理:
一般地,如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f
(a)•f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使
得f(c)=O,这个c也就是f(x)=0的根.
特别提醒:
(1)根据该定理,能确定f(x)在(a,b)内有零点,但零点不一定唯一.
(2)并不是所有的零点都可以用该定理来确定,也可以说不满足该定理的条件,并不能说
明函数在(a,b)上没有零点,例如,函数f(x)=x2﹣3x+2有f(0)•f(3)>0,但函
数f(x)在区间(0,3)上有两个零点.
(3)若f(x)在[a,b]上的图象是连续不断的,且是单调函数,f(a).f(b)<0,则f
(x)在(a,b)上有唯一的零点.
2、函数零点个数的判断方法:
(1)几何法:对于不能用求根公式的方程,可以将它与函数 y=f(x)的图象联系起来,
并利用函数的性质找出零点.
特别提醒:
①“方程的根”与“函数的零点”尽管有密切联系,但不能混为一谈,如方程x2﹣2x+1=0
在[0,2]上有两个等根,而函数f(x)=x2﹣2x+1在[0,2]上只有一个零点;
②函数的零点是实数而不是数轴上的点.
(2)代数法:求方程f(x)=0的实数根.
七.指数式与对数式的互化
【基础知识】
ab=N⇔logaN=b;
alogaN=N;log aN=N
a
指数方程和对数方程主要有以下几种类型:(1)af(x)=b⇔f(x)=log
a
b;log
a
f(x)=b⇔f(x)=ab(定义法)
(2)af(x)=ag(x) ⇔f(x)=g(x);log
a
f(x)=log
a
g(x)⇔f(x)=g(x)>0(同底
法)
(3)af(x)=bg(x) ⇔f(x)log
m
a=g(x)log
m
b;(两边取对数法)
(4)log
a
f(x)=log
b
g(x)⇔log
a
f(x)= ;(换底法)
(5)Alog x+Blog x+C=0(A(ax)2+Bax+C=0)(设t=log x或t=ax)(换元法)
a a
八.对数的运算性质
【基础知识】
对数的性质:① =N;②log aN=N(a>0且a≠1).
a
log (MN)=log M+log N; log =log M﹣log N;
a a a a a a
log Mn=nlog M; log = log M.
a a a a
九.换底公式的应用
【基础知识】
换底公式及换底性质:
(1)log N= (a>0,a≠1,m>0,m≠1,N>0).
a
(2)log b= ,
a
(3)log b•log c=log c,
a b a(4)log bm= log b.
an a
十.对数函数的定义域
【基础知识】
一般地,我们把函数y=log x(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定
a
义域是(0,+∞),值域是R.
十一.对数函数的值域与最值
【基础知识】
一般地,我们把函数y=log x(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定
a
义域是(0,+∞),值域是R.
定点:函数图象恒过定点(1,0)
十二.对数值大小的比较
【基础知识】
1、若两对数的底数相同,真数不同,则利用对数函数的单调性来比较.
2、若两对数的底数和真数均不相同,通常引入中间变量(1,﹣1,0)进行比较
3、若两对数的底数不同,真数也不同,则利用函数图象或利用换底公式化为同底的再进行
比较.(画图的方法:在第一象限内,函数图象的底数由左到右逐渐增大)
十三.对数函数的单调性与特殊点
【基础知识】
对数函数的单调性和特殊点:
1、对数函数的单调性
当a>1时,y=log x在(0,+∞)上为增函数
a
当0<a<1时,y=log x在(0,+∞)上为减函数
a2、特殊点
对数函数恒过点(1,0)
十四.对数函数图象与性质的综合应用
【基础知识】
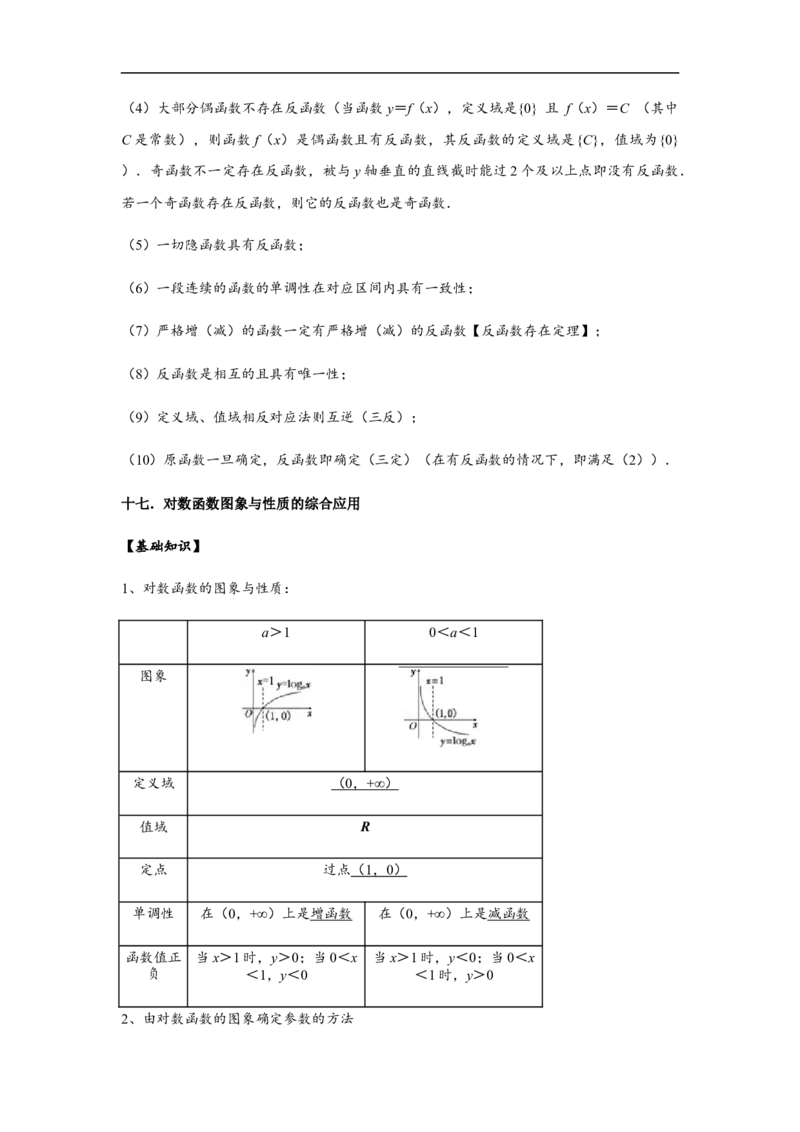
1、对数函数的图象与性质:
a>1 0<a<1
图象
定义域 ( 0 , +∞ )
值域 R
定点 过点 ( 1 , 0 )
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
函数值正 当x>1时,y>0;当0<x 当x>1时,y<0;当0<x
负 <1,y<0 <1时,y>0
2、由对数函数的图象确定参数的方法
已知对数型函数的图象研究其解析式及解析式中所含参数的取值范围问题,通常是观
察图象,获得函数的单调性、对称性、奇偶性、经过的特殊点等,由此确定函数解析式以
及其中所含参数的取值范围.
【技巧方法】
1、4种方法﹣﹣解决对数运算问题的方法
(1)将真数化为底数(或已知对数的数)的幂的积,再展开;(2)将同底对数的和、差、倍合并;
(3)利用换底公式将不同底的对数式转化成同底的对数式,要注意换底公式的正用、逆用
及变形应用;
(4)利用常用对数中的lg 2+lg 5=1.
2、3个基本点﹣﹣对数函数图象的三个基本点
(1)当a>1时,对数函数的图象“上升”;当0<a<1时,对数函数的图象“下降”.
(2)对数函数y=log x(a>0,且a≠1)的图象过定点(1,0),且过点(a,1),(
a
,﹣1)函数图象只在第一、四象限.
(3)底数的大小与对数函数的图象位置之间的关系.
3、2个应用﹣﹣对数函数单调性的应用
(1)比较对数式的大小:
①若底数为同一常数,则可由对数函数的单调性直接进行判断;若底数为同一字母,需对
底数进行分类讨论.
②若底数不同,真数相同,则可以先用换底公式化为同底后,再进行比较.
③若底数与真数都不同,则常借助1,0等中间量进行比较.
(2)解对数不等式:
形如log x>log b的不等式,借助y=log x的单调性求解,如果a的取值不确定,需分a>1
a a a
与0<a<1两种情况讨论.形如log x>b的不等式,需先将b化为以a为底的对数式的形
a
式.
十五.指数函数与对数函数的关系
【基础知识】
指数函数和对数函数的关系:(1)对数函数与指数函数互为反函数,它们的定义域、值域互换,图象关于直线y=x对
称.
(2)它们都是单调函数,都不具有奇偶性.当a>l时,它们是增函数;当O<a<l时,
它们是减函数.
(3)指数函数与对数函数的联系与区别:
十六.反函数
【基础知识】
【定义】一般地,设函数y=f(x)(x∈A)的值域是C,根据这个函数中x,y 的关系,
用y把x表示出,得到x=g(y).若对于y在中的任何一个值,通过x=g(y),x在A中
都有唯一的值和它对应,那么,x=g(y)就表示y是自变量,x是因变量是y的函数,这
样的函数y=g(x)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作y=f(﹣1)(x)
反函数y=f(﹣1)(x)的定义域、值域分别是函数y=f(x)的值域、定义域.
【性质】
反函数其实就是y=f(x)中,x和y互换了角色
(1)函数f(x)与他的反函数f﹣1(x)图象关于直线y=x对称;函数及其反函数的图形
关于直线y=x对称
(2)函数存在反函数的重要条件是,函数的定义域与值域是一一映射;
(3)一个函数与它的反函数在相应区间上单调性一致;(4)大部分偶函数不存在反函数(当函数y=f(x),定义域是{0} 且 f(x)=C (其中
C是常数),则函数f(x)是偶函数且有反函数,其反函数的定义域是{C},值域为{0}
).奇函数不一定存在反函数,被与y轴垂直的直线截时能过2个及以上点即没有反函数.
若一个奇函数存在反函数,则它的反函数也是奇函数.
(5)一切隐函数具有反函数;
(6)一段连续的函数的单调性在对应区间内具有一致性;
(7)严格增(减)的函数一定有严格增(减)的反函数【反函数存在定理】;
(8)反函数是相互的且具有唯一性;
(9)定义域、值域相反对应法则互逆(三反);
(10)原函数一旦确定,反函数即确定(三定)(在有反函数的情况下,即满足(2)).
十七.对数函数图象与性质的综合应用
【基础知识】
1、对数函数的图象与性质:
a>1 0<a<1
图象
定义域 ( 0 , +∞ )
值域 R
定点 过点 ( 1 , 0 )
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
函数值正 当x>1时,y>0;当0<x 当x>1时,y<0;当0<x
负 <1,y<0 <1时,y>0
2、由对数函数的图象确定参数的方法已知对数型函数的图象研究其解析式及解析式中所含参数的取值范围问题,通常是观
察图象,获得函数的单调性、对称性、奇偶性、经过的特殊点等,由此确定函数解析式以
及其中所含参数的取值范围.
【解题方法点拨】
1、4种方法﹣﹣解决对数运算问题的方法
(1)将真数化为底数(或已知对数的数)的幂的积,再展开;
(2)将同底对数的和、差、倍合并;
(3)利用换底公式将不同底的对数式转化成同底的对数式,要注意换底公式的正用、逆用
及变形应用;
(4)利用常用对数中的lg 2+lg 5=1.
2、3个基本点﹣﹣对数函数图象的三个基本点
(1)当a>1时,对数函数的图象“上升”;当0<a<1时,对数函数的图象“下降”.
(2)对数函数y=log x(a>0,且a≠1)的图象过定点(1,0),且过点(a,1),(
a
,﹣1)函数图象只在第一、四象限.
(3)底数的大小与对数函数的图象位置之间的关系.
3、2个应用﹣﹣对数函数单调性的应用
(1)比较对数式的大小:
①若底数为同一常数,则可由对数函数的单调性直接进行判断;若底数为同一字母,需对
底数进行分类讨论.
②若底数不同,真数相同,则可以先用换底公式化为同底后,再进行比较.
③若底数与真数都不同,则常借助1,0等中间量进行比较.
(2)解对数不等式:形如log x>log b的不等式,借助y=log x的单调性求解,如果a的取值不确定,需分a>1
a a a
与0<a<1两种情况讨论.形如log x>b的不等式,需先将b化为以a为底的对数式的形
a
式.
十八.函数的零点
【基础知识】
一般地,对于函数y=f(x)(x∈R),我们把方程f(x)=0的实数根x叫作函数y=
f(x)(x∈D)的零点.即函数的零点就是使函数值为0的自变量的值.函数的零点不是一
个点,而是一个实数.
十九.函数零点的判定定理
【基础知识】
1、函数零点存在性定理:
一般地,如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f
(a)•f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使
得f(c)=O,这个c也就是f(x)=0的根.
【技巧方法】
(1)根据该定理,能确定f(x)在(a,b)内有零点,但零点不一定唯一.
(2)并不是所有的零点都可以用该定理来确定,也可以说不满足该定理的条件,并不能说
明函数在(a,b)上没有零点,例如,函数f(x)=x2﹣3x+2有f(0)•f(3)>0,但函
数f(x)在区间(0,3)上有两个零点.
(3)若f(x)在[a,b]上的图象是连续不断的,且是单调函数,f(a).f(b)<0,则f
(x)在(a,b)上有唯一的零点.
2、函数零点个数的判断方法:
(1)几何法:对于不能用求根公式的方程,可以将它与函数 y=f(x)的图象联系起来,
并利用函数的性质找出零点.
特别提醒:①“方程的根”与“函数的零点”尽管有密切联系,但不能混为一谈,如方程x2﹣2x+1=0
在[0,2]上有两个等根,而函数f(x)=x2﹣2x+1在[0,2]上只有一个零点;
②函数的零点是实数而不是数轴上的点.
(2)代数法:求方程f(x)=0的实数根.
二十.函数的零点与方程根的关系
【基础知识】
函数的零点表示的是函数与x轴的交点,方程的根表示的是方程的解,他们的含义是不一
样的.但是,他们的解法其实质是一样的.
二十一. 二分法
【基础知识】
二分法 即一分为二的方法.设函数f(x)在[a,b]上连续,且满足f(a)•f(b)<
0,我们假设f(a)<0,f(b)>0,那么当x = 时,若f(x )=0,这说x 为零点;
1 1 1
若不为0,假设大于0,那么继续在[x ,b]区间取中点验证它的函数值为0,一直重复下去,
1
直到找到满足要求的点为止.这就是二分法的基本概念.
习题演练
一.选择题(共12小题)
1.已知函数 ,则不等式 的解集是
A. B.
C. D.2.下列式子计算正确的是( )
A.m3•m2=m6 B.(﹣m)2=
C.m2+m2=2m2 D.(m+n)2=m2+n2
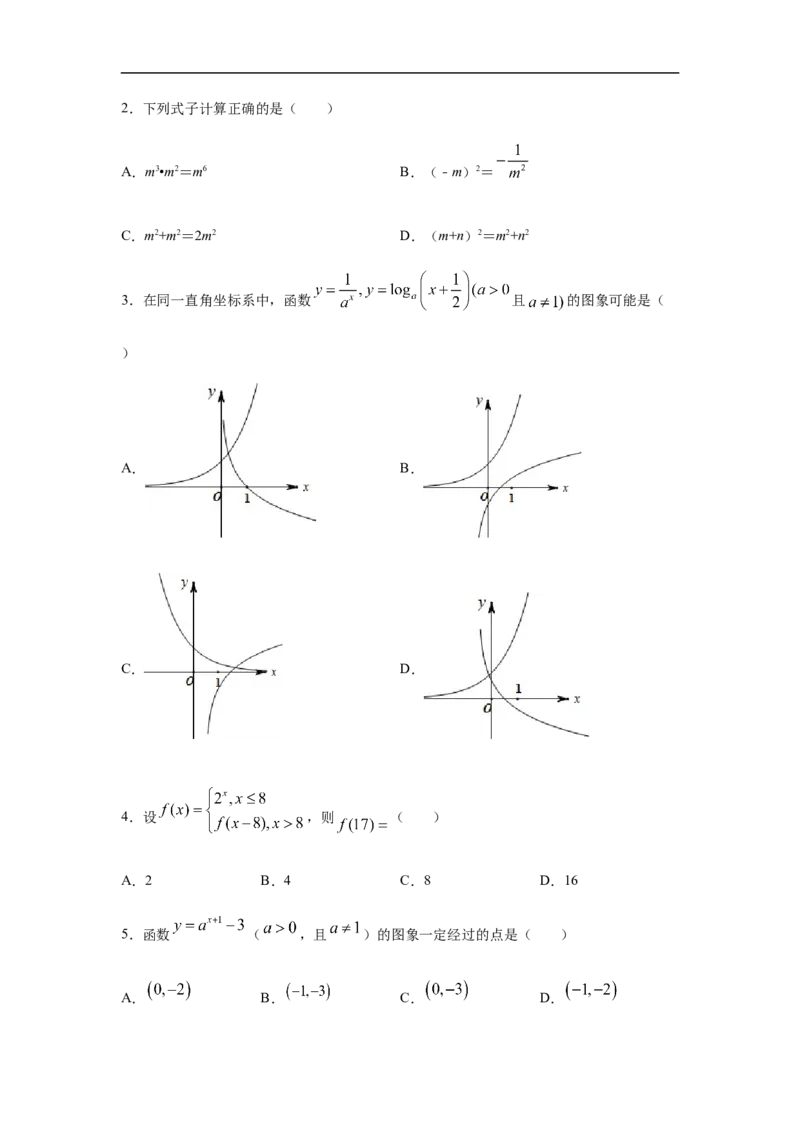
3.在同一直角坐标系中,函数 且 的图象可能是(
)
A. B.
C. D.
4.设 ,则 ( )
A.2 B.4 C.8 D.16
5.函数 ( ,且 )的图象一定经过的点是( )
A. B. C. D.6.设 , ,则( )
A. B.
C. D.
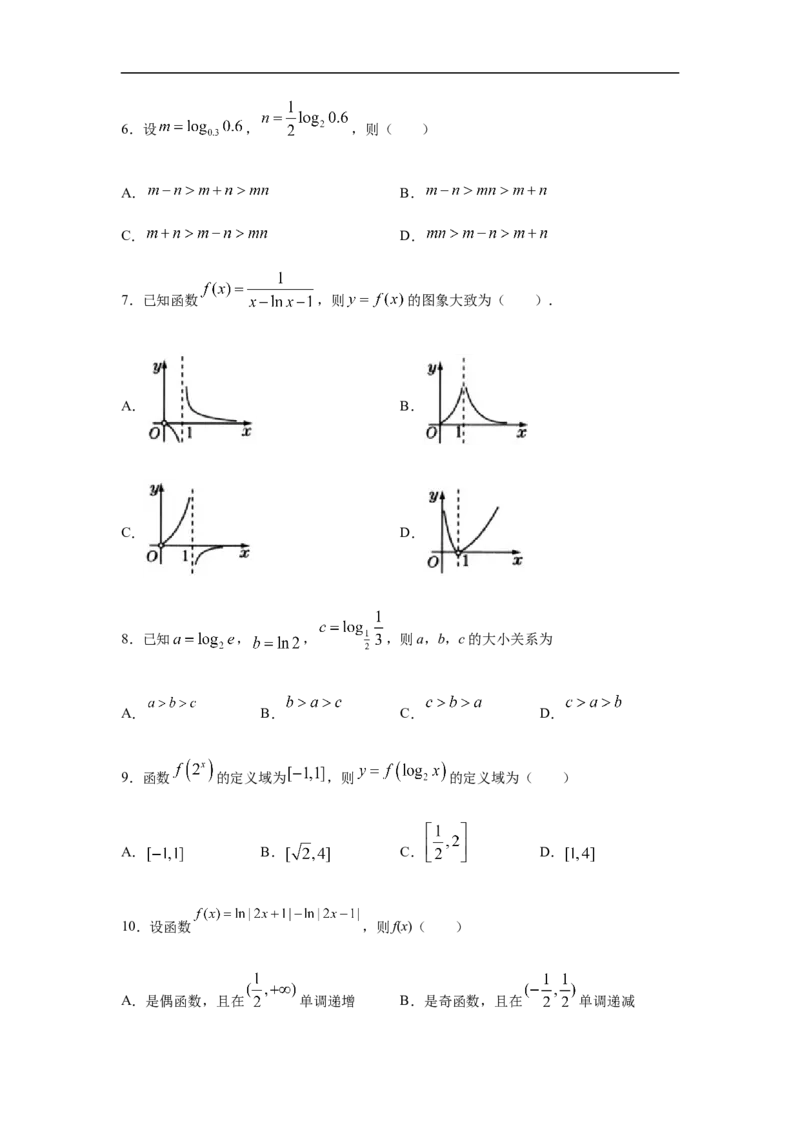
7.已知函数 ,则 的图象大致为( ).
A. B.
C. D.
8.已知 , , ,则a,b,c的大小关系为
A. B. C. D.
9.函数 的定义域为 ,则 的定义域为( )
A. B. C. D.
10.设函数 ,则f(x)( )
A.是偶函数,且在 单调递增 B.是奇函数,且在 单调递减C.是偶函数,且在 单调递增 D.是奇函数,且在 单调递减
11.已知函数 , ,若方程 有4
个不相等的实根,则实数 的取值范围是( )
A. B. C. D.
12.在下列区间中,函数 的零点所在的区间为( )
A. B. C. D.
二.填空题(共6小题)
13.计算: __________.
14.不等式 对任意 恒成立,则实数a的取值范围为____________.
15.已知当 时,不等式 恒成立,则实数 的取值范围为
________.
16.若关于 的方程 的解集为空集,求实数 的取值范围______.
17.已知函数 ,则函数 的零点个数为_________.
18.已知定义在 上的函数 满 ,当 时, ,则 _______.
三.解析题(共6小题)
19.已知函数 .
(1)求函数 的定义域;
(2)求函数 的零点;
(3)若函数 的最小值为-4,求 的值.
20.已知定义域为 的函数, 是奇函数.
(1)求 , 的值;
(2)若对任意的 ,不等式 恒成立,求实数 的取值范围.
21.设 ,且 .
(1)求 的值;
(2)求 在区间 上的最大值.
22.已知实数 ,定义域为 的函数 是偶函数,其中 为自然对数的
底数.
(Ⅰ)求实数 值;(Ⅱ)判断该函数 在 上的单调性并用定义证明;
(Ⅲ)是否存在实数 ,使得对任意的 ,不等式 恒成立.若存
在,求出实数 的取值范围;若不存在,请说明理由.
23.函数 对任意的实数m,n,有 ,当 时,有
.
(1)求证: .
(2)求证: 在 上为增函数.
(3)若 ,解不等式 .
24.甲商店某种商品4月份(30天,4月1日为第一天)的销售价格P(元)与时间t
(天)的函数关系如图所示(1),该商品日销售量Q(件)与时间t(天)的函数关系如
图(2)所示.
(1) (2)
(1)写出图(1)表示的销售价格与时间的函数关系式 ,写出图(2)表示的日
销售量与时间的函数关系式 及日销售金额M(元)与时间的函数关系式.
(2)乙商店销售同一种商品,在4月份采用另一种销售策略,日销售金额N(元)与时间
t(天)之间的函数关系式为 ,试比较4月份每天两商店销售金额的
大小关系。