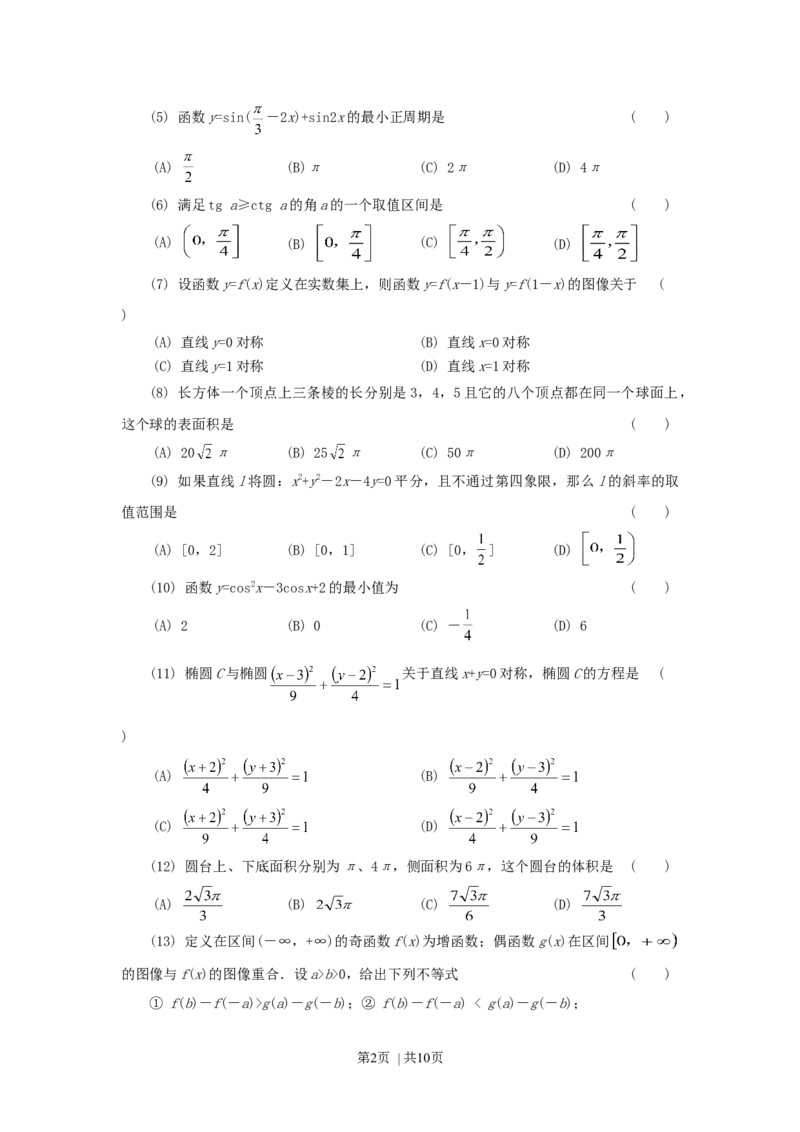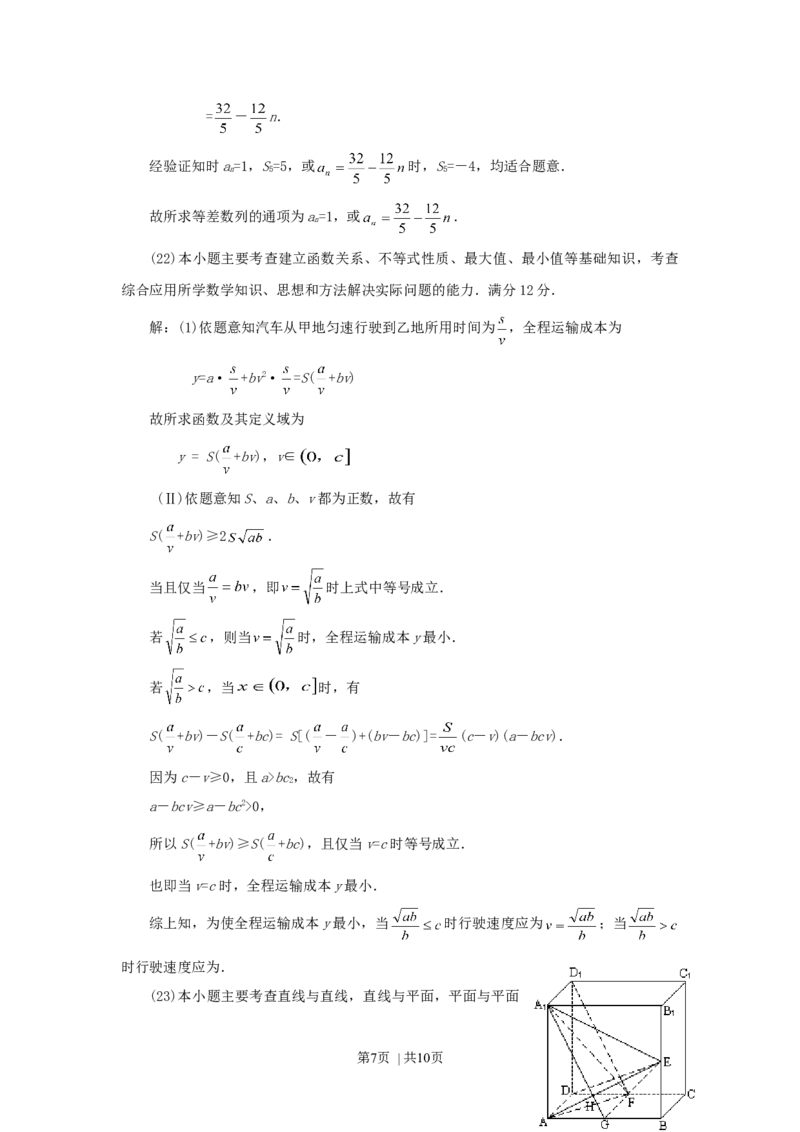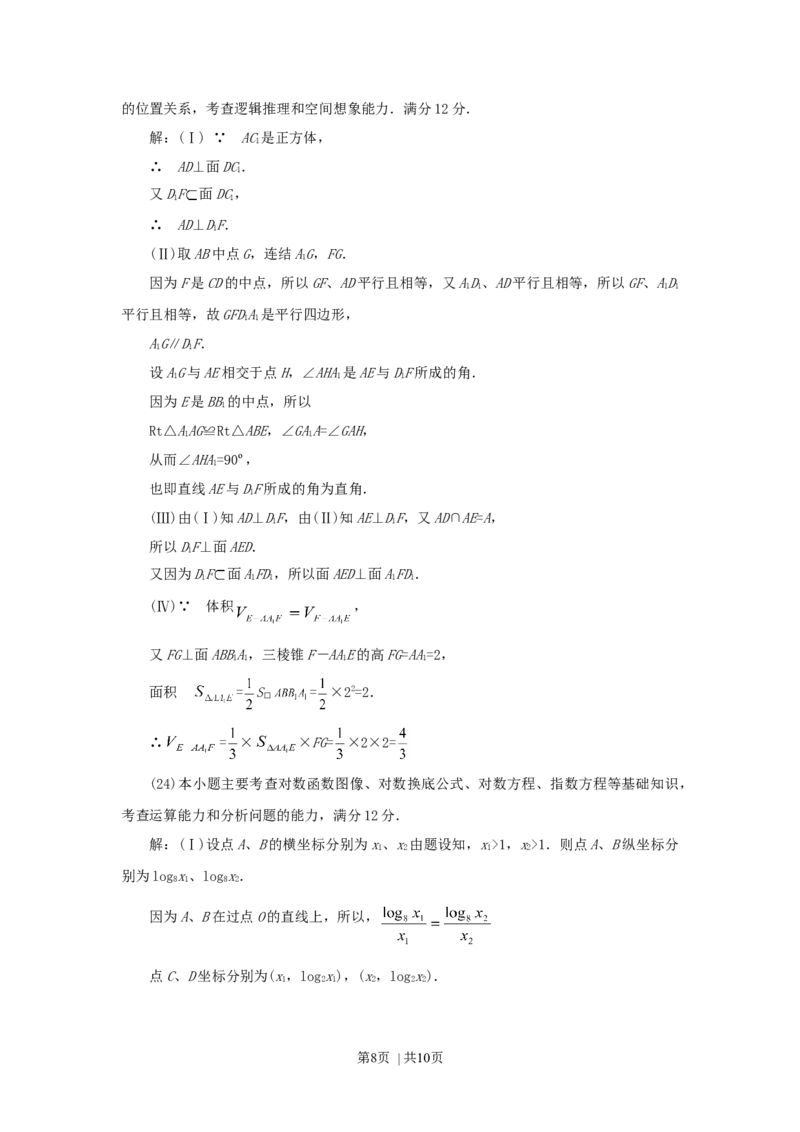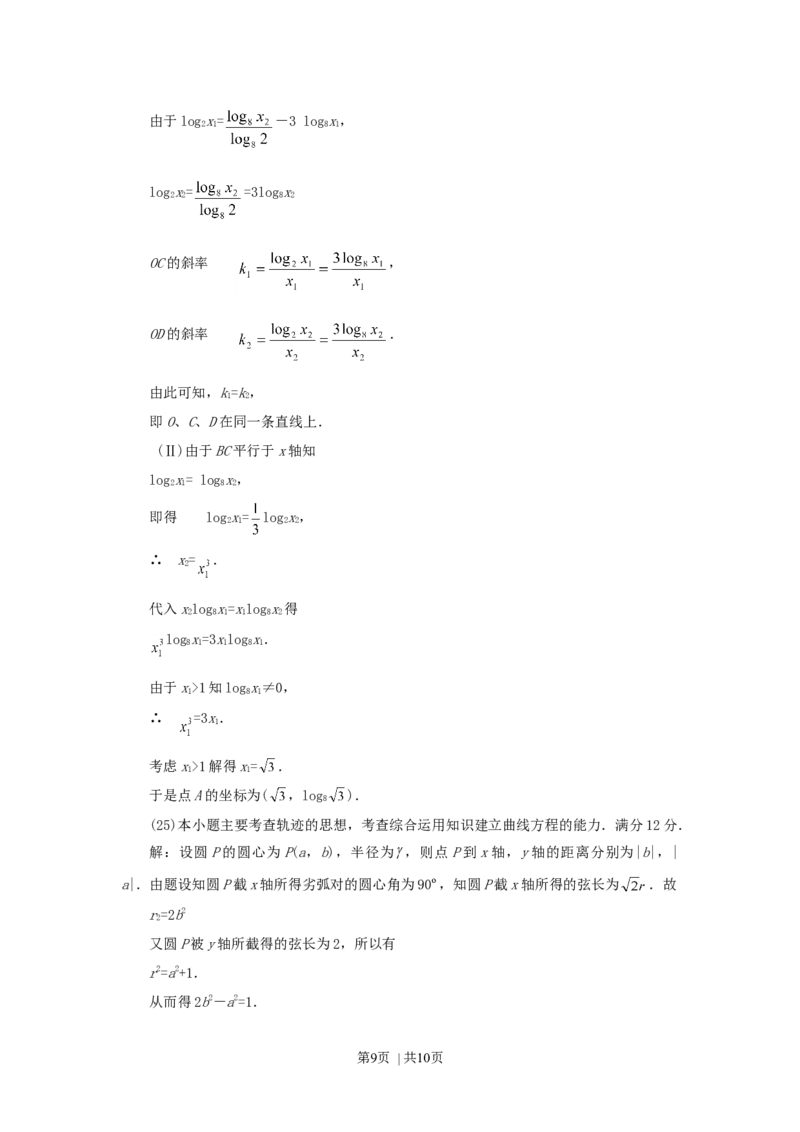文档内容
1997 年天津高考文科数学真题及答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至8
页.共150分.考试时间120分钟.
第Ⅰ卷(选择题共65分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在试题卷上.
3.考试结束,监考人将本试卷和答题卡一并收回.
一、选择题:本大题共15小题;第(1)—(10)题每小题4分,第(11)—(15)题每小题5分,
共65分.在每小题给出的四个选项中,只有一项是符合题目要求的
王新奎新疆屯敞
(1) 设集合M={x|0≤x<2},集合N={x|x2-2x-3<0},集合M∩N= ( )
(A) {x|0≤x<1} (B) {x|0≤x<2}
(C) {x|0≤x≤1} (D) {x|0≤x≤2}
(2) 如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a= ( )
(A) -3 (B) -6 (C) - (D)
(3) 函数y=tg 在一个周期内的图像是 ( )
(4) 已知三棱锥D—ABC的三个侧面与底面全等,且AB=AC= ,BC=2,则以BC为棱,
以面BCD与面BCA为面的二面角的大小是 ( )
(A) (B) (C) (D)
第1页 | 共10页(5) 函数y=sin( -2x)+sin2x的最小正周期是 ( )
(A) (B)π (C) 2π (D) 4π
(6) 满足tg a≥ctg a的角a的一个取值区间是 ( )
(A) (B) (C) (D)
(7) 设函数y=f(x)定义在实数集上,则函数y=f(x-1)与y=f(1-x)的图像关于 (
)
(A) 直线y=0对称 (B) 直线x=0对称
(C) 直线y=1对称 (D) 直线x=1对称
(8) 长方体一个顶点上三条棱的长分别是 3,4,5且它的八个顶点都在同一个球面上,
这个球的表面积是 ( )
(A) 20 π (B) 25 π (C) 50π (D) 200π
(9) 如果直线l将圆:x2+y2-2x-4y=0平分,且不通过第四象限,那么l的斜率的取
值范围是 ( )
(A) [0,2] (B) [0,1] (C) [0, ] (D)
(10) 函数y=cos2x-3cosx+2的最小值为 ( )
(A) 2 (B) 0 (C) - (D) 6
(11) 椭圆C与椭圆 关于直线x+y=0对称,椭圆C的方程是 (
)
(A) (B)
(C) (D)
(12) 圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是 ( )
(A) (B) (C) (D)
(13) 定义在区间(-∞,+∞)的奇函数f(x)为增函数;偶函数g(x)在区间
的图像与f(x)的图像重合.设a>b>0,给出下列不等式 ( )
① f(b)-f(-a)>g(a)-g(-b);② f(b)-f(-a) < g(a)-g(-b);
第2页 | 共10页③ f(a)-f(-b)>g(b)-g(-a);④ f(a)-f(-b)bc,故有
2
a-bcv≥a-bc2>0,
所以S( +bv)≥S( +bc),且仅当v=c时等号成立.
也即当v=c时,全程运输成本y最小.
综上知,为使全程运输成本y最小,当 时行驶速度应为 ;当
时行驶速度应为.
(23)本小题主要考查直线与直线,直线与平面,平面与平面
第7页 | 共10页的位置关系,考查逻辑推理和空间想象能力.满分12分.
解:(Ⅰ) ∵ AC是正方体,
1
∴ AD⊥面DC.
1
又DF 面DC,
1 1
∴ AD⊥DF.
1
(Ⅱ)取AB中点G,连结AG,FG.
1
因为F是CD的中点,所以GF、AD平行且相等,又AD、AD平行且相等,所以GF、AD
1 1 1 1
平行且相等,故GFDA是平行四边形,
1 1
AG∥DF.
1 1
设AG与AE相交于点H,∠AHA是AE与DF所成的角.
1 1 1
因为E是BB的中点,所以
1
Rt△AAG≌Rt△ABE,∠GAA=∠GAH,
1 1
从而∠AHA=90º,
1
也即直线AE与DF所成的角为直角.
1
(Ⅲ)由(Ⅰ)知AD⊥DF,由(Ⅱ)知AE⊥DF,又AD∩AE=A,
1 1
所以DF⊥面AED.
1
又因为DF 面AFD,所以面AED⊥面AFD.
1 1 1 1 1
(Ⅳ)∵ 体积 ,
又FG⊥面ABBA,三棱锥F-AAE的高FG=AA=2,
1 1 1 1
面积 = S = ×22=2.
□
∴ = × ×FG= ×2×2=
(24)本小题主要考查对数函数图像、对数换底公式、对数方程、指数方程等基础知识,
考查运算能力和分析问题的能力,满分12分.
解:(Ⅰ)设点A、B的横坐标分别为x、x由题设知,x>1,x>1.则点A、B纵坐标分
1 2 1 2
别为logx、logx.
8 1 8 2
因为A、B在过点O的直线上,所以,
点C、D坐标分别为(x,logx),(x,logx).
1 2 1 2 2 2
第8页 | 共10页由于logx= -3 logx,
2 1 8 1
logx= =3logx
2 2 8 2
OC的斜率 ,
OD的斜率 .
由此可知,k=k,
1 2
即O、C、D在同一条直线上.
(Ⅱ)由于BC平行于x轴知
logx= logx,
2 1 8 2
即得 logx= logx,
2 1 2 2
∴ x= .
2
代入xlogx=xlogx得
2 8 1 1 8 2
logx=3xlogx.
8 1 1 8 1
由于x>1知logx≠0,
1 8 1
∴ =3x.
1
考虑x>1解得x= .
1 1
于是点A的坐标为( ,log ).
8
(25)本小题主要考查轨迹的思想,考查综合运用知识建立曲线方程的能力.满分12分.
解:设圆P的圆心为P(a,b),半径为 ,则点P到x轴,y轴的距离分别为|b|,|
a|.由题设知圆P截x轴所得劣弧对的圆心角为90º,知圆P截x轴所得的弦长为 .故
r=2b2
2
又圆P被y轴所截得的弦长为2,所以有
r2=a2+1.
从而得2b2-a2=1.
第9页 | 共10页又因为P(a,b)到直线x-2y=0的距离为 ,所以 ,
即有 a-2b=±1,
由此有
解方程组得
于是r2=2b2=2,
所求圆的方程是
(x+1)2+(y+1)2=2,或(x-1)2+(y-1)2=2.
第10页 | 共10页