文档内容
2024-2025 学年浙江省宁波市六校高一下学期 4 月期中考试数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数z满足z=2i+1,则z2的虚部为 ( )
A. −3 B. 2i C. 4 D. 4i
2.在 中,设 ⃗ ⃗, ⃗ ⃗, ⃗ ⃗ , ⃗ ⃗ ,则 ⃗ ( )
△ABC
AB=a AC=b BD=2DC AE=4ED BE=
11⃗ 8 ⃗ 1⃗ 8 ⃗ 1⃗ 8 ⃗ 11⃗ 8 ⃗
A. a− b B. a− b C. − a+ b D. − a+ b
15 15 3 15 3 15 15 15
3.如图所示,用符号语言可表达为( )
A. α⋂β=m,n⊂α,m⋂n=A;
B. α⋂β=m,n∈α,m⋂n=A;
C. α⋂β=m,n⊂α,A⊂m,A⊂n;
D. α⋂β=m,n∈α,A∈m,A∈n;
4.下面关于空间几何体的叙述:①底面是正多边形的棱锥是正棱锥;②有两个面互相平行,其余各面都是
梯形的多面体是棱台;③正四棱柱都是长方体;④直角三角形以其直角边所在直线为轴旋转一周形成的几
何体是圆锥;⑤平行六面体是六棱柱.其中叙述正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
5.在△ABC中,已知B=120°,AC=√19,AB=2,则BC= ( )
A. 5 B. 3 C. √2 D. 1
6.为了测量某一塔ED的高,小明在山下A处测得塔尖点D的仰角为45°,再沿AC方向前进24.4米到达山
脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,那么此塔高约为 ( )(√3≈1.7,√2≈1.4)
第 页,共 页
1 1A. 37.54 B. 38.23 C. 39.53 D. 40.52
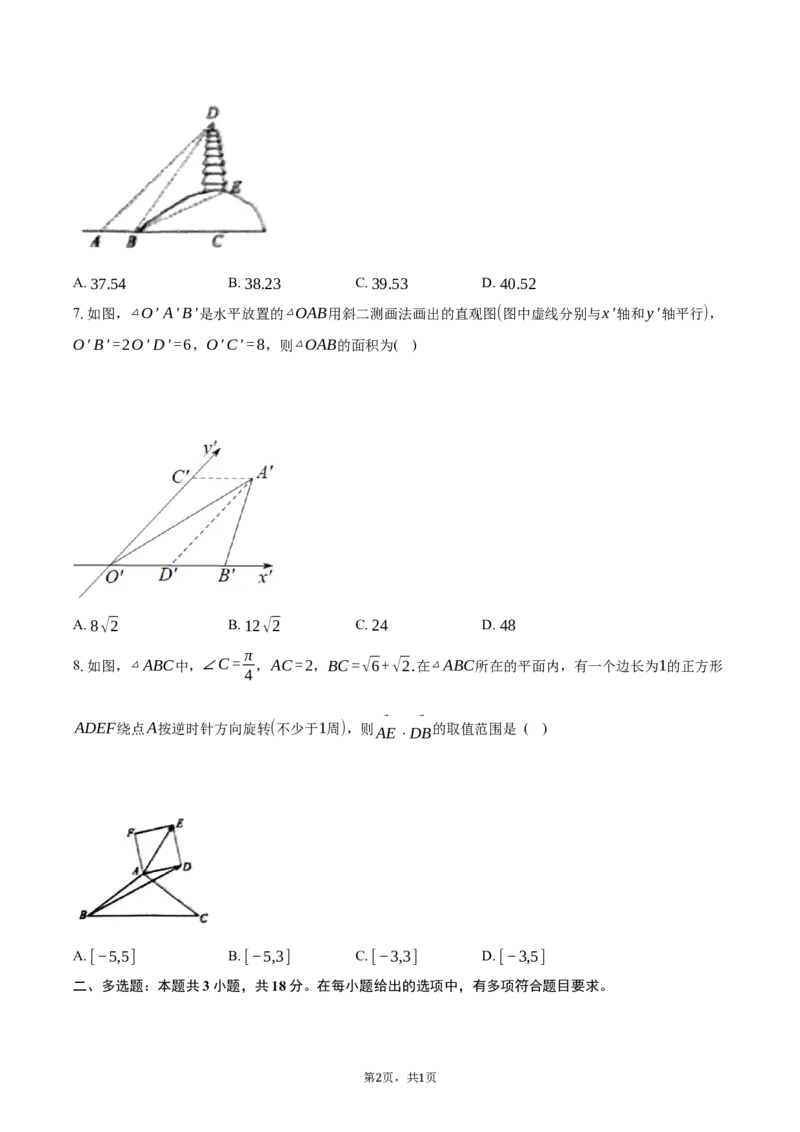
7.如图,△O′ A′B′是水平放置的△OAB用斜二测画法画出的直观图(图中虚线分别与x′轴和y′轴平行),
O′B′=2O′D′=6,O′C′=8,则△OAB的面积为( )
A. 8√2 B. 12√2 C. 24 D. 48
π
8.如图,△ABC中,∠C= ,AC=2,BC=√6+√2.在△ABC所在的平面内,有一个边长为1的正方形
4
⃗ ⃗
ADEF绕点A按逆时针方向旋转(不少于1周),则 的取值范围是 ( )
AE⋅DB
A. [−5,5] B. [−5,3] C. [−3,3] D. [−3,5]
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
第 页,共 页
2 19.已知⃗ ,⃗ ,则下列结论中正确的是 ( )
a=(3,−1) b=(1,2)
A. ⃗ ⃗
|a+b|=√17
√2
B. ⃗a与⃗b的夹角余弦值为
5
C. 与 同向共线的单位向量是(√5 2√5)
⃗b ,
5 5
D. 向量 在向量 上的投影向量为(1 2)
⃗a ⃗b ,
5 5
10.在△ABC中,内角A,B,C的对边分别为a,b,c,下列说法中正确的是 ( )
A. 若sin2A=sin2B,则△ABC为等腰三角形
B. 若
A
⃗
B⋅A
⃗
C=2
, a=2 ,则 b2+c2=8
C. 若△ABC为锐角三角形,则sinA>cosB
π
D. 若b=8,c=10,B= ,则△ABC解的个数为2
3
11.在意大利,有一座满是“斗笠”的灰白小镇阿尔贝罗贝洛,这些圆锥形屋顶的奇特小屋名叫Trulli,于
1996年被收入世界文化遗产名录.现测量一个Trulli的屋顶,得到圆锥SO(其中S为顶点,O为底面圆心),
母线SA的长为6m,C是母线SA上靠近点S的三等分点.从点A到点C绕屋顶侧面一周安装灯光带,灯光
带的最小长度为2√13m.下面说法正确的是 ( )
A. 圆锥SO的侧面积为12πm2
B. 过点S的平面截此圆锥所得截面面积最大值为8√2m2
C. 圆锥SO的外接球的表面积为72πm2
D. 棱长为√3m的正四面体在圆锥SO内可以任意转动
三、填空题:本题共3小题,每小题5分,共15分。
12.已知i是虚数单位,则|2+i2+2i3|=________.
⃗ ⃗
13.如图,设Ox,Oy是平面内相交成60°角的两条数轴,e ,e 分别是与x轴、y轴正方向同向的单位向量.
1 2
第 页,共 页
3 1⃗ ⃗ ⃗ ⃗ ⃗
若向量p=OP=xe + ye ,则把有序数对(x,y)叫做向量 p 在斜坐标系Oxy中的坐标.设向量⃗a,⃗b在斜坐
1 2
⃗ ⃗
标系xOy中的坐标分别为(2,1),(−3,2),则 a⋅b=________.
a
14.在△ABC中,内角A,B,C对应的边分别为a,b,c,若2sin2C=sin2A+sin2B,则 的取值范围
b
为________.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知平面向量⃗ ⃗ ⃗ .
a=(1,−3),b=(2,x),c=(−3,x+5)
(1)
若⃗
a⊥
(⃗
a+
⃗
b
),求|⃗
b
|;
(2) 若(⃗
a+
⃗
b
)
//
⃗
c
,求向量 ⃗a与⃗b 的夹角.
16.(本小题15分)
已知复数z=1+mi(i是虚数单位,m∈R),且z⋅(3+i)为纯虚数.
m+2i
(Ⅰ)设复数z = ,求|z |;
1 1−i 1
a−i2025
(Ⅱ)设复数z = ,且复数z 所对应的点在第一象限,求实数a的取值范围.
2 z 2
17.(本小题15分)
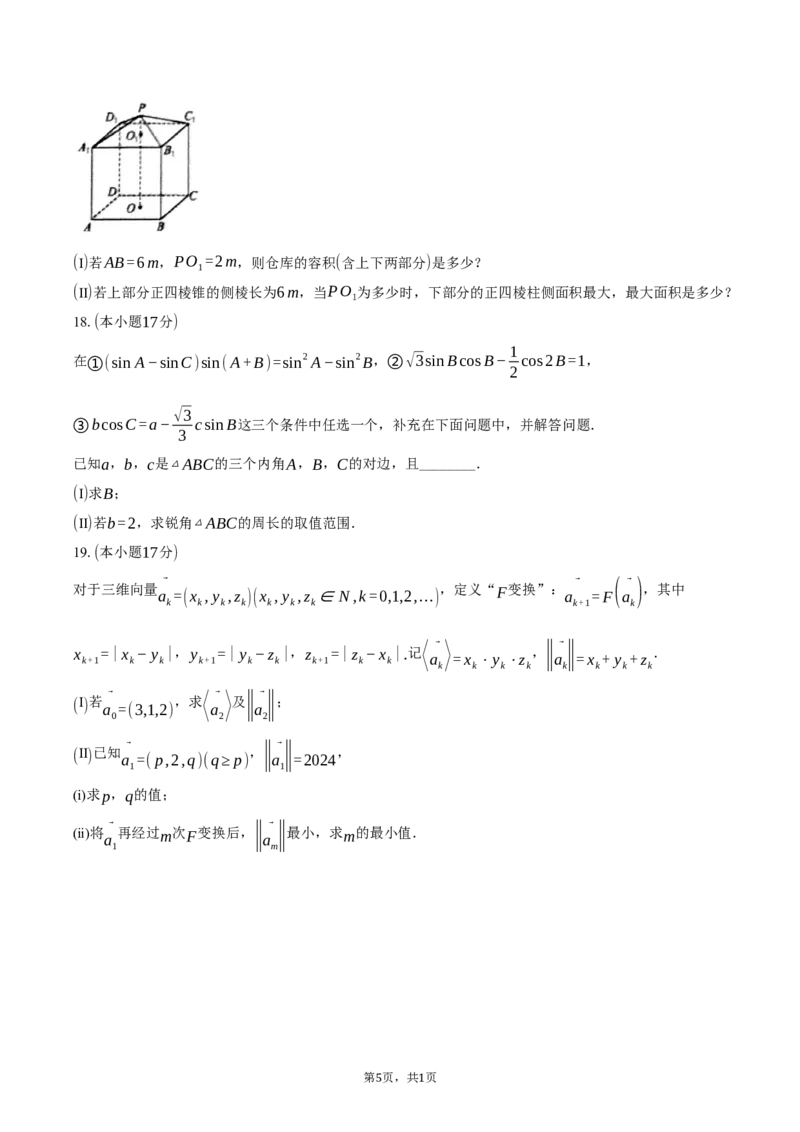
现需要设计一个仓库,由上、下两部分组成,如图所示,上部分的形状是正四棱锥P−A B C D ,下部
1 1 1 1
分的形状是正四棱柱ABCD−A B C D ,要求正四棱柱的高O O是正四棱锥的高PO 的4倍.
1 1 1 1 1 1
第 页,共 页
4 1(Ⅰ)若AB=6m,PO =2m,则仓库的容积(含上下两部分)是多少?
1
(Ⅱ)若上部分正四棱锥的侧棱长为6m,当PO 为多少时,下部分的正四棱柱侧面积最大,最大面积是多少?
1
18.(本小题17分)
1
在①(sin A−sinC)sin(A+B)=sin2A−sin2B,②√3sinBcosB− cos2B=1,
2
√3
③bcosC=a− csinB这三个条件中任选一个,补充在下面问题中,并解答问题.
3
已知a,b,c是△ABC的三个内角A,B,C的对边,且________.
(Ⅰ)求B;
(Ⅱ)若b=2,求锐角△ABC的周长的取值范围.
19.(本小题17分)
对于三维向量
a
⃗
=(x ,y ,z )(x ,y ,z ∈N,k=0,1,2,…)
,定义“F变换”:
a
⃗
=F
(
a
⃗),其中
k k k k k k k k+1 k
x =|x −y |,y =|y −z |,z =|z −x |.记⟨⃗ ⟩ ,‖⃗‖ .
k+1 k k k+1 k k k+1 k k a =x ⋅y ⋅z a =x + y +z
k k k k k k k k
(Ⅰ) 若
a
⃗
=(3,1,2)
,求⟨
a
⃗ ⟩及‖
a
⃗‖;
0 2 2
(Ⅱ) 已知
a
⃗
=(p,2,q)(q≥p)
,‖
a
⃗‖
=2024
,
1 1
(ⅰ)求p,q的值;
(ⅱ)将⃗再经过m次F变换后,‖⃗‖最小,求m的最小值.
a a
1 m
第 页,共 页
5 1参考答案
1.C
2.D
3.A
4.B
5.B
6.B
7.D
8.D
9.ACD
10.BC
11.ABD
12.√5
7
13.−
2
14.(2−√3,2+√3)
15.解: (1) 因为⃗
a⊥
(⃗
a+
⃗
b
),
所以⃗ (⃗ ⃗) ,
a⋅ a+b =0
即⃗ ⃗ ⃗ ,
a2+a⋅b=0
则 ,
1+(−3) 2+1×2−3x=0
即10+2−3x=0,
所以x=4,
所以⃗ ,
b=(2,4)
所以|⃗| ;
b =√22+42=2√5
由题意可得⃗ ⃗
(2) a+b=(3,x−3)
又因(⃗
a+
⃗
b
)
//
⃗
c
,所以3(x+5)=−3(x−3) ,
第 页,共 页
6 1解得x=−1,
所以⃗ ,
b=(2,−1)
⃗ ⃗
⟨⃗ ⃗⟩ a⋅b
所以cos a,b = ,
⃗ ⃗
|a|⋅|b|
即 ⟨⃗ ⃗⟩ 2+3 √2,
cos a,b = =
√10⋅√5 2
又因为⃗ ⃗ ,
a,b∈[0,π]
⃗ ⃗ π
所以a,b= .
4
16.解: , − .
∵z=1+mi
∴z=1−mi
−
∴z⋅(3+i)=(1−mi)(3+i)
=(3+m)+(1−3m)i.
又 − 为纯虚数,
∵z⋅(3+i)
{ 3+m=0
∴ ,解得m=−3,
1−3m≠0
∴z=1−3i.
−3+2i 5 1
(Ⅰ)z = =− − i,
1 1−i 2 2
√26
∴|z |= ;
1 2
(Ⅱ)∵z=1−3i,
a−i (a+3)+(3a−1)i
∴z = = ,
2 1−3i 10
又∵复数z 所对应的点在第一象限,
2
{ a+3>0 1
∴ ,解得:a> .
3a−1>0 3
第 页,共 页
7 117.解:(1)∵PO =2m,正四棱柱的高O O是正四棱锥的高PO 的4倍.
1 1 1
∴O O=8m,
1
1
所以仓库的容积V = ×62×2+62×8=312m3,
3
(2)若正四棱锥的侧棱长为6m,设PO =xm,
1
则 , , ,
O O=4xm A O =√36−x2m A B =√2√36−x2m
1 1 1 1 1
正四棱柱侧面积 ,
∴ S=4⋅4x⋅√2√36−x2=16√2x⋅√36−x2 (00,可得cosB− sinB=0,即tanB=√3,
3
π
因为02 时, ⃗ 的三个分量为 t−2,2,t 这三个数,
a
k+1
|| ⃗ || ||⃗||
所以 a = a −4 .
k+1 k
当 t=2 时,⃗ 的三个分量为 2,2,4 ,
a
k
则 ⃗ 的三个分量为 ⃗ 的三个分量为
2,0,2
,
a 0,2,2,a
k+1 k+2
|| ⃗ || || ⃗ ||
所以 a = a =⋯=4 .
k+1 k+2
||⃗|| || ⃗ || || ⃗ ||
所以,由
a =2024
,可得
a =8, a =4
.
1 505 506
因为
a
⃗
=(1010,2,1012)
,所以任意
a
⃗ 的三个分量始终为偶数,且都有一个分量等于
2
.
1 k
所以 ⃗ 的三个分量只能是
2,2,4
三个数,
a
505
⃗ 的三个分量只能是
0,2,2
三个数.
a
506
|| ⃗ || || ⃗ ||
所以当m<505 时,
a ≥8
;当m≥505 时,
a =4
.
m+1 m+1
所以m 的最小值为505.
第 页,共 页
10 1