文档内容
浙江省衢州市 2024-2025 学年高一上学期 1 月教学质量检测数学试题
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3},B={0,2,4},则A∩B=( )
A. {0} B. {2} C. {1,2} D. {0,1,2,3,4}
2.已知幂函数f(x)的图象过点(2,√2),则f(9)=( )
A. -3 B. √3 C. 2 D. 3
3.“x>0”是“ex>1”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.下列不等关系成立的是( )
π π π π
A. 3-0.3>20.1 B. log 3>log 2 C. sin >tan D. cos >cos(- )
2 3 3 4 2 3
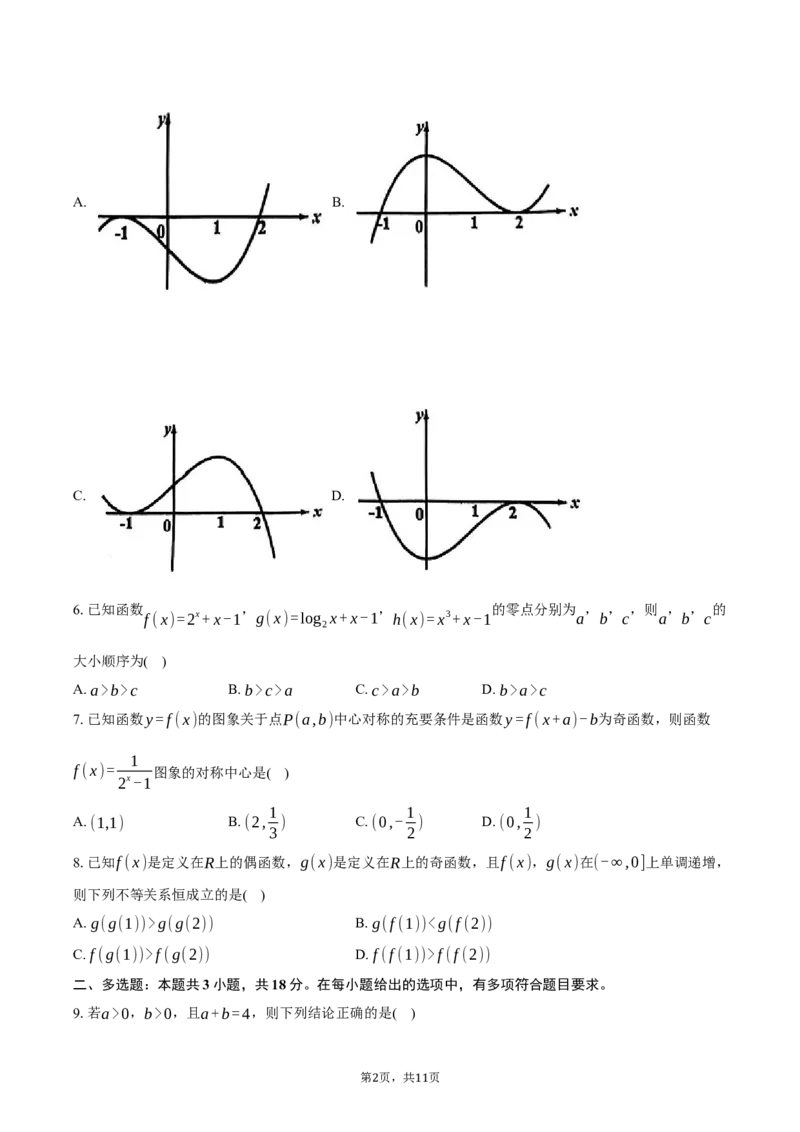
5.函数 的部分图象大致为( )
f(x)=(x+1) 2 (x-2)
第 页,共 页
1 11A. B.
C. D.
6.已知函数 , , 的零点分别为 , , ,则 , , 的
f(x)=2x+x-1 g(x)=log x+x-1 h(x)=x3+x-1 a b c a b c
2
大小顺序为( )
A. a>b>c B. b>c>a C. c>a>b D. b>a>c
7.已知函数y=f(x)的图象关于点P(a,b)中心对称的充要条件是函数y=f(x+a)-b为奇函数,则函数
1
f(x)= 图象的对称中心是( )
2x-1
1 1 1
A. (1,1) B. (2, ) C. (0,- ) D. (0, )
3 2 2
8.已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且f(x),g(x)在(-∞,0]上单调递增,
则下列不等关系恒成立的是( )
A. g(g(1))>g(g(2)) B. g(f(1))f(g(2)) D. f(f(1))>f(f(2))
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.若a>0,b>0,且a+b=4,则下列结论正确的是( )
第 页,共 页
2 11A. 2a ⋅2b=16 B. √ab≤2
1 1
C. log a+log b≥2 D. + ≥1
2 2 a b
10.已知函数f(x)=sin(cosx)-cos(sinx),则( )
A. f(x)是奇函数 B. f(x)图象有对称轴
C. f(x)是周期函数 D. f(1)<0
11.已知正实数 , 满足{ x4=1+x ,则( )
x y
y8=3x+ y
5
A. y>1 B. x< C. y2<√2 D. y0
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
第 页,共 页
3 114
在平面直角坐标系xOy中,角α是第二象限角,且终边与单位圆交于点P(m, ).
5
(1)求实数m及tanα的值;
3
cos(-α)+cos( π-α)
2
(2)求 的值.
π
sin(π-α)+sin( +α)
2
16.(本小题15分)
已知函数 且 .
f(x)=log (-x2+ax-3)(a>0 a≠1)
a
(1)若a=4,求函数f(x)的定义域及值域;
(2)若函数f(x)在(1,3)上单调递增,求实数a的取值范围.
17.(本小题15分)
π π
已知函数f(x)=asin(2x- )+b(a>0,b∈R)在区间[0, ]上的值域为[0,3].
6 2
(1)求函数f(x)的解析式;
π π
(2)若对任意x ∈[0, ],存在x ∈[ ,m]使得f(x )≥f(x ),求实数m的取值范围.
1 6 2 2 1 2
18.(本小题17分)
1
已知函数f(x)=a(x+1)+ ,a∈R.
x
(1)讨论函数f(x)的单调性(无需证明);
若 ,解关于 的不等式
(2) a<0 x f(|x-2|)>f(x2 );
若关于 的方程 有两个不同的解,求实数 的取值范围.
(3) x f(3x+1)=1 a
19.(本小题17分)
设点集D是集合M={(x,y)|x,y∈R}的一个非空子集,若按照某种对应法则f,D中的每一点(x,y)
都有唯一的实数t与之对应,则称f为D上的二元函数,记为t=f(x,y).当二元函数f(x,y)满足对任意x,
y,z∈R,均有:①f(x,y)=f(y,x);②f(x,x)=0;③f(x,z)+f(z,y)≥f(x,y)成立,则称二元
函数f(x,y)具有性质P.
(1)试判断二元函数f(x,y)=|x- y|是否具有性质P,并说明理由;
(2)若f(x,y)具有性质P,证明:函数g(x,y)=√f(x,y)具有性质P;
第 页,共 页
4 11对任意具有性质 的函数 ,均可推出 f(x,y) 具有性质 ,求实数 的取值范围.
(3) P f(x,y) F(x,y)= P m
m+√f(x,y)
第 页,共 页
5 11答案和解析
1.B
【解析】∵A={1,2,3},B={0,2,4},
∴A∩B={2}.
故选B.
2.D
【解析】设 ,
f(x)=xα
1
由f(2)=2α=√2,得α= ,
2
1
,
∴f(x)=x2
1
则 .
f(9)=92=3
故选D.
3.C
【解析】由ex>1,得x>0,反之也成立,
所以“x>0”是“ex>1”的充要条件.
故选C.
4.B
【解析】对于A、3-0.3<30=1,20.1>20=1,则3-0.3<20.1,故A错误;
对于B、log 3>log 2=1,log 2log 2,故B正确;
2 2 3 3 2 3
π √3 π π π
对于C、sin = ,tan =1,则sin 2时,f(x)>0,
由选项可知,只有A满足题意,
故选A.
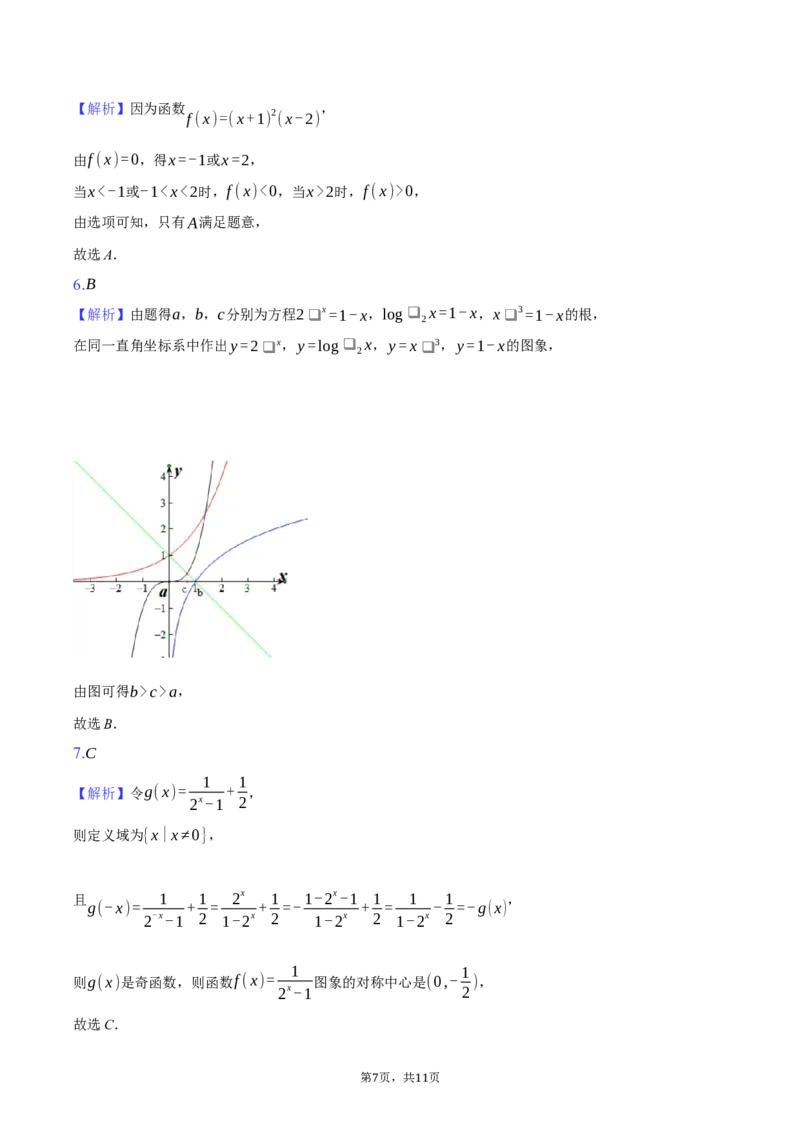
6.B
【解析】由题得a,b,c分别为方程2 ❑ x=1-x,log ❑ x=1-x,x ❑ 3=1-x的根,
2
在同一直角坐标系中作出y=2 ❑ x,y=log ❑ 2 x,y=x ❑ 3,y=1-x的图象,
由图可得b>c>a,
故选B.
7.C
1 1
【解析】令g(x)= + ,
2x-1 2
则定义域为{x|x≠0},
且 1 1 2x 1 1-2x-1 1 1 1 ,
g(-x)= + = + =- + = - =-g(x)
2-x-1 2 1-2x 2 1-2x 2 1-2x 2
1 1
则g(x)是奇函数,则函数f(x)= 图象的对称中心是(0,- ),
2x-1 2
故选C.
第 页,共 页
7 118.C 【解析】由题意,得f(x)在(0,+∞)递减,g(x)在R上递增,且g(0)=0,
对于A、因为g(2)>g(1),则g(g(2))>g(g(1)),故A错误;
对于B、因为f(1)>f(2),则g(f(1))>g(f(2)),故B错误;
对于C、因为g(2)>g(1)>0,则f(g(1))>f(g(2)),故C正确;
对于D、因为f(1)>f(2),若f(1)>f(2)>0,则f(f(1))0
可得 ,
y8- y= y(y7-1)=3x>0
又y>0,则y7-1>0,故y>1,故A正确;
x>0,则x4=x+1>1,则x4>1,即x>1,
令 , ,
f(x)=x4-x-1 x>1
则正实数x为f(x)=0的解,即为f(x)的零点,
,
f(x)=x4-x-1=x(x3-1)-1
x>1,x3-1>0,且函数y=x与y=x3-1都单调递增,
故 在 时单调递增,
f(x)=x4-x-1 x>1
5 625 5 625-320-256 49
f(1)=-1<0,f( )= - -1= = >0,
4 256 4 256 256
5 5
故f(x)在(1, )上存在零点,即11,则g(y)∈(3, ),
4
,
g(y)= y8- y= y(y7-1)
由y>1,y7-1>0,且函数s= y,s= y7-1均单调递增,
故 在 单调递增,
g(y)= y8- y y>1
第 页,共 页
9 11时, ,
11,可知4-√4 2<3,即此时g(y)∉(3, ),
4
故y2>√2,故C错误;
由{ x4=1+x ,得{x8=x2+2x+1,即{x8-x=x2+x+1
,
y8=3x+ y y8=3x+ y y8- y=3x
5
由10,
4
故x2+x+1>3x,即x8-x>y8- y,即g(x)>g(y),
又y>1时,g(y)单调递增,且x>1,y>1,故x>y,故D正确.
故选ABD.
12.2
【解析】由ln(log m)=0得log m=1,所以m=2;
2 2
故答案为2.
13.6π
1
【解析】玉璜的面积为 ×(π+2π)×4=6π,
2
故答案为6π.
14.[-3π,-2π)
【解析】由sinx=0得x=kπ(k∈Z),
若 无零点,则 ,得 ,此时 满足条件的零点
① f(x)=x2-2x+2a+5 (-2) 2-4(2a+5)<0 a>-2 f(x)=sinx
最多1个,不合题意;
若 只一个零点,则 ,此时 满足条件的零点最多 个,不合题意;
② f(x)=x2-2x+2a+5 a=-2 f(x)=sinx 1
5
③若f(x)=x2-2x+2a+5有两个零点,一个正数,另一个为零,则a=- ,此时f(x)=sinx满足条件的
2
零点只1个,不合题意;
第 页,共 页
10 11若 有两个正零点,则{(-2) 2-4(2a+5)>0,则 5 ,此时 满
④ f(x)=x2-2x+2a+5 - 0 2
足条件的零点有1个,不合题意;
5
⑤若f(x)=x2-2x+2a+5有两个零点,一个正零点,另一个为负零点,2a+5<0,此时a<- ,
2
{-2π>a
则f(x)=sinx满足条件的零点必须有3个 ,得-3π⩽a<-2π.
-3π⩽a
综上:a∈[-3π,-2π).
故答案为[-3π,-2π).
4 4
15.解(1)因为角α与单位圆交于点P(m, ),所以sinα= ,cosα=m,
5 5
又角α为第二象限角,且sin2α+cos2α=1,
4
3
所以m=cosα=-√1-sin2α=- ,所以 5 4.
5 tanα= =-
m 3
3
cos(-α)+cos( π-α)
2 cosα-sinα 1-tanα
(2) = = =-7.
π sinα+cosα tanα+1
sin(π-α)+sin( +α)
2
16.解: 当 时, ,
(1) a=4 f(x)=log (-x2+4x-3)
4
令-x2+4x-3>0⇒11时,t=-x2+ax-3在(1,3)上为增函数且-x2+ax-3>0在(1,3)上恒成立,
第 页,共 页
11 11a>1
{
所以 a
{ ⩾3 ⇒a⩾6,
2
-1+a-3⩾0
当00在(1,3)上恒成立,
00,故- +b≤f(x)≤a+b,
2
{ a
依题意则 - +b=0,解得{a=2,
2
b=1
a+b=3
π
故f(x)=2sin(2x- )+1;
6
(2)由题意可知f(x ) ≥f(x ) ,
1 min 2 min
π
因为x ∈[0, ],
1 6
π π π
所以- ≤2x - ≤ ,
6 1 6 6
1 π 1
则- ≤sin(2x- )≤ ,
2 6 2
第 页,共 页
12 11故f(x ) =0,
1 min
π 1
则f(x ) ≤0即sin(2x - ) ≤- ,
2 min 2 6 min 2
π 5π π π
又x ∈[ ,m]所以 ≤2x - ≤2m- ,
2 2 6 2 6 6
π 7π 2π
则2m- ≥ ,解得m≥ ,
6 6 3
2π
故m的取值范围为[ ,+∞).
3
18.解:(1)f(x)定义域为{x|x≠0},
1
当a=0时,f(x)= 在(-∞,0)和(0,+∞)上单调递减;
x
1
当a<0时,f(x)=ax+ +a在(-∞,0)和(0,+∞)上单调递减;
x
1 √a √a
当a>0时,f(x)=ax+ +a在(-∞,- )和( ,+∞)上单调递增;
x a a
√a √a
在(- ,0)和(0, )上单调递减;
a a
(2)由f(x)的定义域知|x-2|>0,x2>0,得x≠2且x≠0,
1
又由(1)知当a<0时,f(x)=ax+ +a在(0,+∞)上单调递减;
x
故 ,
f(|x-2|)>f(x2 )⇔|x-2|2 或{ x<2 ,即 或 ,
x<-2 x>1
x-2f(x2 ) {x|x<-2 12}
(3)令t=3x+1,则其在R上单调递增,且t>1.
第 页,共 页
13 11则方程 有两个不同解等价于方程 在 上有两个不同解,
f(3x+1)=1 f(t)=1 (1,+∞)
1
f(t)=a(t+1)+ =1在(1,+∞)上有两个不同解.
t
t-1
即a= 在(1,+∞)上有两个不同解.
t(t+1)
m m
令m=t-1∈(0,+∞),则a= = ,
(m+1)(m+2) m2+3m+2
1 2
故 =m+ +3在m∈(0,+∞)上有两个不同解,
a m
2
又y=m+ +3在(0,√2)上递减,(√2,+∞)上递增,
m
1
则 >3+2√2,即00
m+√f(x,y)
故 ,即 ,
√f(x,y)>-m>0 f(x,y)>(-m) 2>0
取 得 与 矛盾,故 不满足题意.
y=x f(x,x)>(-m) 2>0 f(x,x)=0 m<0
若 ,则 f(x,y) ,故 ,得 与 矛盾,
(ii) m=0 F(x,y)= √f(x,y)≠0 √f(x,x)≠0 f(x,x)=0
√f(x,y)
故m=0不满足题意.
若 ,由 f(x,y) f(y,x) ,
(iii) m>0 F(x,y)= = =F(y,x)
m+√f(x,y) m+√f(y,x)
f(x,x) ,从而性质 满足,
F(x,x)= =0 ①②
m+√f(x,x)
下面考虑性质③.记f(x,z)=a,f(z,y)=b,f(x,y)=c,
易知a≥0,b≥0,c≥0,
a b c
下证当a+b>c时,均有 + > ,
m+√a m+√b m+√c
x m2
令p(x)= ,则p(x)=m+√x+ -2m,
m+√x m+√x
由复合函数单调性可知p(x)在[0,+∞)单调递增,
1∘若a,b之中至少有一个大于c,不妨a>c,故p(a)>p(c),
a c b
即 > ,又 ≥0,
m+√a m+√c m+√b
第 页,共 页
15 11a b c
故 + > 成立.
m+√a m+√b m+√c
2∘若a,b均不超过c,即a≤c,b≤c,
a b a b a+b c
则 + ≥ + = > ,
m+√a m+√b m+√c m+√c m+√c m+√c
从而m>0时,恒有F(x,z)+F(z,y)≥F(x,y)成立,
即此时 f(x,y) 具有性质 ,
F(x,y)= P
m+√f(x,y)
故m>0满足题意.
第 页,共 页
16 11