文档内容
第一次月考 B 卷
高一数学·全解全析
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知命题 :向量 , 所在的直线平行,命题 :向量 , 平行,则 是 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】因为向量 , 所在的直线平行时,可得向量 , 平行,则充分性成立,
而向量 , 平行时,向量 , 所在的直线平行或重合,则必要性不成立,
则命题 是 的充分不必要条件,故选:A.
2.设复数z满足 ,则 ( )
A. B.2 C. D.
【答案】A
【解析】由复数z满足 ,则 ,
即 ,故选:A.
3.已知点 , ,向量 , ,则 与 的夹角的余弦值为( )
A. B. C. D.
【答案】A【解析】由题意,得 , ,
则 与 的夹角的余弦值为 .故选:A.
4.在 中,内角A,B,C所对的边分别是a,b,c,且 ,则 的形状为( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰三角形或直角三角形
【答案】A
【解析】 ,由正弦定理,得 ,
即
∴ ,可得 ,
又 ,∴ ,
则 的形状为等腰三角形.故选:A.
5.在平行四边形ABCD中,已知 , , , ,则 ( ).
A. B. C.6 D.9
【答案】A
【解析】由题意可得: , ,
∵ ,①
,②
①-②得: ,即 ,
∴ .故选:A.
6.在锐角 中,角A,B,C所对的边分别为a,b,c.已知 ,且 ,则
的取值范围是( )A. B. C. D.
【答案】B
【解析】∵ ,即: , ,
∴ ,
∴由正弦定理得: ,即: ,
∴ ,
∴ 或 ,解得: 或 (舍),
又∵△ABC为锐角三角形,则 ,
∴ ,解得: ,
∴ ,
又∵ ,∴ ,
∴ ,
∴ ,即 的取值范围 .故选:B.
7.17世纪法国数学家费马在给朋友的一封信中曾提出一个关于三角形的有趣问题:在三角形所在平面内,
求一点,使它到三角形每个顶点的距离之和最小.现已证明:在 中,若三个内角均小于 ,则当
点 满足 时,点 到三角形三个顶点的距离之和最小,点 被人们称为费
马点.根据以上知识,已知 为平面内任意一个向量, 和 是平面内两个互相垂直的向量,且
,则 的最小值是( )
A. B.
C. D.
【答案】B【解析】设 , , ,
则 ,
即为点 到 和点 三个点的距离之和,
则△ABC为等腰三角形,如图,
由费马点的性质可得,需满足:点P在y轴上且∠APB=120°,则∠APO=60°,
因为|OA|=|OB|=2,则 ,所以点 坐标为 时,距离之和最小,
最小距离之和为 .故选:B.
8.如图,在边长为4的等边 中,点 为中线 的三等分点(靠近点 ),点 为 的中点,则
( )
A. B. C. D.– 3
【答案】C【解析】由已知, , , ,
所以 .
由已知 是 的中点,所以 ,
, .
所以 ,
,
所以,
.故选:C.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得5分,部分选对的得2分,有选错的得0分。
9.下列说法正确的有( )
A.已知 , ,若 与 共线,则
B.若 , ,则
C.若 ,则 一定不与 共线
D.若 , , 为锐角,则实数 的范围是
【答案】AD
【解析】A选项: , ,若 与 共线,则 , ,A选项正确;B选项:当
时, , ,但 不一定成立,B选项错误;C选项: ,无法确定两个向量的方向,两个向量可能共线,C选项错误;
D选项: , ,若 为锐角,则 ,解得 ,D选项正确;
故选:AD.
10.欧拉公式 是由瑞士著名数学家欧拉创立,该公式将指数函数的定义域扩大到复数集,
建立了三角函数与指数函数的关联,在复变函数论里面占有非常重要的地位,被誉为数学中的天桥.依据
欧拉公式,下列选项中不正确的是( )
A. 对应的点位于第二象限 B. 为纯虚数
C. 的模长等于 D. 的共轭复数为
【答案】ABC
【解析】对于A: , 对应的点位于第二象限,故A正确;对于B:
, 为纯虚数,故B正确;
对于C: ,故C正确;
对于D: ,所以 的共轭复数为 ,故D错误.故选:ABC.
11.如图1是一款家居装饰物——博古架,它始见于北宋宫廷、官邸.博古架是类似于书架式的木器,其每
层形状不规则,前后均敞开,无板壁封挡,便于从各个位置观赏架上放置的器物.某博古架的部分示意图如
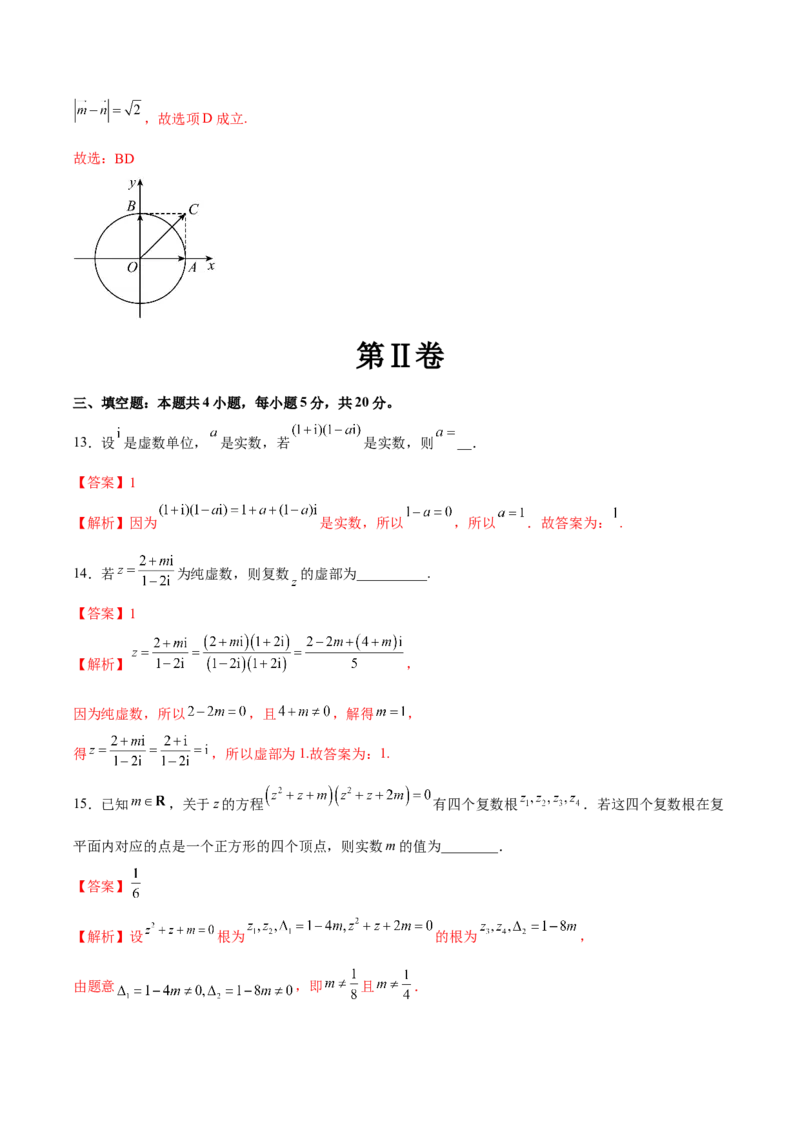
图2中实线所示,网格中每个小正方形的边长为1,则下列结论正确的是( )A.
B.若 ,则
C.
D.设Z为线段AK上任意一点,则 的取值范围是
【答案】AD
【解析】以A为坐标原点,AD,AJ所在直线分别为x,y轴建立如图所示的平面直角坐标系.
A选项:易知 , , , ,所以 , ,
则 ,所以 ,所以A正确.
B选项:易知 , , , ,
, ,所以 , , ,所以 ,得 ,解得 , ,所以 ,所以B错误.
C选项:由选项A,B知 ,则 ,
, ,所以C错误.
D选项:易知 , ,设 ,则 , ,
所以 .因为 ,所以当 时, 取得最小值
;当 时, 取得最大值40.所以 的取值范围是 ,所以D正确. 故选:AD.
12.已知向量 , ,且 ,则下列说法正确的是( )
A. B.
C. D. 的值为
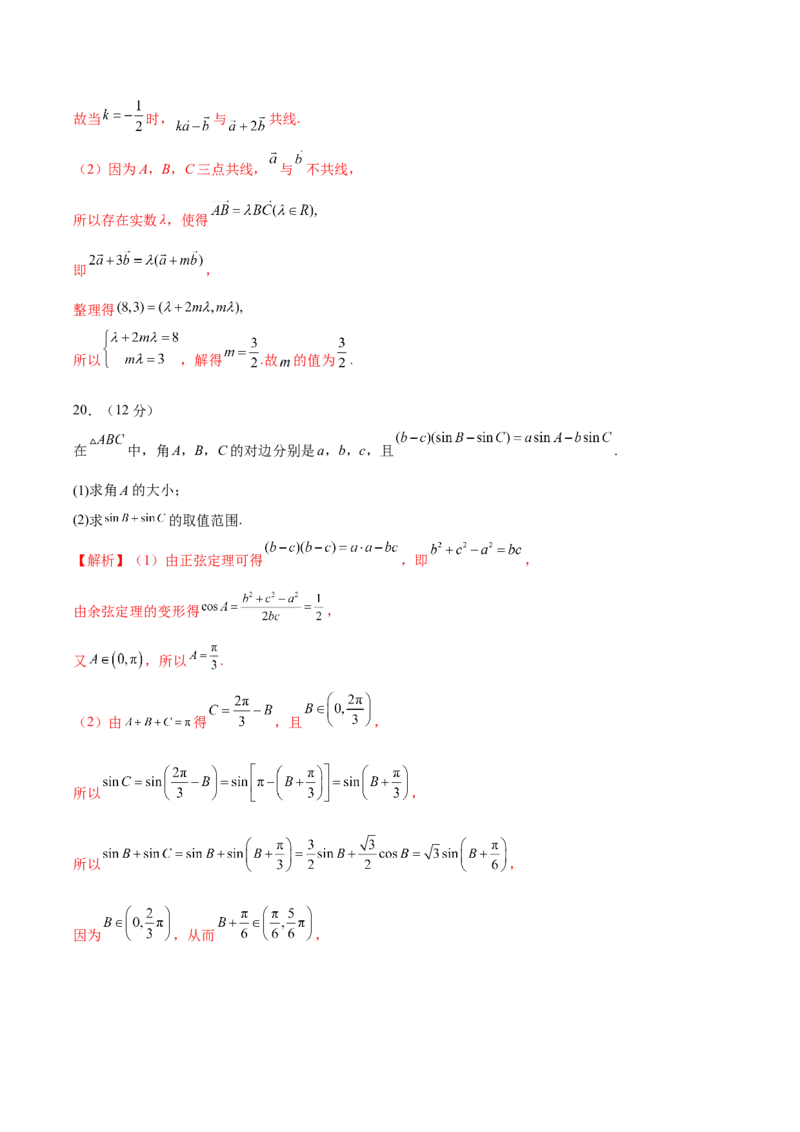
【答案】BD
【解析】 , ,即有 ,故选项A错误;
不妨设 ,如图,设点 、 、 的坐标为 , , ,即可得点 , 在单位
圆 上.
根据向量加法的平行四边形法则,四边形 为正方形,据此不妨设 , ,从而可得:
, ,即可得选项B成立,选项C错误.
由 可得: ,可得: , ,则可得:,故选项D成立.
故选:BD
第Ⅱ卷
三、填空题:本题共4小题,每小题5分,共20分。
13.设 是虚数单位, 是实数,若 是实数,则 __.
【答案】1
【解析】因为 是实数,所以 ,所以 .故答案为: .
14.若 为纯虚数,则复数 的虚部为__________.
【答案】1
【解析】 ,
因为纯虚数,所以 ,且 ,解得 ,
得 ,所以虚部为1.故答案为:1.
15.已知 ,关于z的方程 有四个复数根 .若这四个复数根在复
平面内对应的点是一个正方形的四个顶点,则实数m的值为________.
【答案】
【解析】设 根为 的根为 ,
由题意 ,即 且 .①当 时, 均为实数,则四个实数根均在实轴上,矛盾;
②当 时, 为实数且 为虚数,且 ,
所以 ;
此时 ,故 或 ,
且 或 ,
这四个点为以 为中心,且对角线的方程分别为 , ,对角线的长度为 的正方形的顶
点.
③当 时, 均为虚数,
因为 为实数,故 为共轭复数且 ,故 的实部为 ,
同理 的实部为 ,,即四个对应点均在直线 ,这与题设矛盾.
综上: .故答案为: .
16.若关于x的方程 无实根,则实数p的取值范围是______.
【答案】
【解析】若方程 无实根,即: 无实根,
假定方程有实数根,而 为实数,则 ,且 ,
解得 或 ,因此原方程无实数根时, 且 ,
故实数p的取值范围是 .故答案为:
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步棸。
17.(10分)
已知复数 , ,其中 为非零实数.
(1)若 是实数,求 的值;
(2)若 ,复数 为纯虚数,求实数 的值;
【解析】(1)∵ 为实数,
∴ ,又∵ 为非零实数,∴ .
(2)∵ ,∴ ,
∴ 为纯虚数,
∴ ∴m的值为2.
18.(12分)
复数 , , 为虚数单位, ;
(1)若 是实数,求 的值;
(2)若复数 、 对应的向量分别是 、 ,存在 使等式 成立,求实数 的取值范围.
【解析】(1) ,
因为 为实数,所以 , ,结合θ范围,解得 ,所以 .
(2)复数 ,
复数 、 对应的向量分别是 , , ,
,
又 ,
,
所以
,得 ,
因为 ,所以 ,所以 .
所以 ,解得 或 .
所以实数 的取值范围是 .
19.(12分)
已知 .
(1)当k为何值时, 与 共线?
(2)若 且A,B,C三点共线,求m的值.
【解析】(1)
因为 与 共线,
所以 解得 .故当 时, 与 共线.
(2)因为A,B,C三点共线, 与 不共线,
所以存在实数λ,使得
即 ,
整理得
所以 ,解得 .故 的值为 .
20.(12分)
在 中,角A,B,C的对边分别是a,b,c,且 .
(1)求角A的大小;
(2)求 的取值范围.
【解析】(1)由正弦定理可得 ,即 ,
由余弦定理的变形得 ,
又 ,所以 .
(2)由 得 ,且 ,
所以 ,
所以 ,
因为 ,从而 ,所以 ,从而 .
即 的取值范围为 .
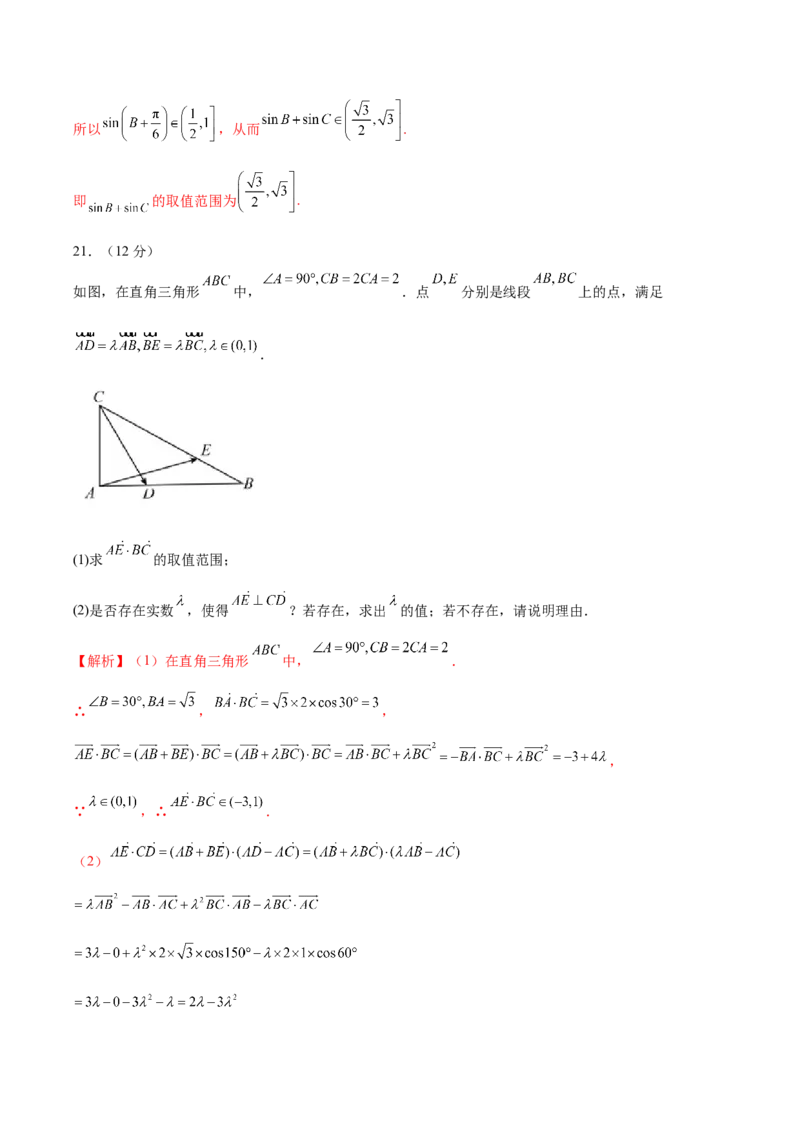
21.(12分)
如图,在直角三角形 中, .点 分别是线段 上的点,满足
.
(1)求 的取值范围;
(2)是否存在实数 ,使得 ?若存在,求出 的值;若不存在,请说明理由.
【解析】(1)在直角三角形 中, .
∴ , ,
,
∵ ,∴ .
(2)令 ,得 或 (舍).
∴存在实数 ,使得 .
22.已知 的内角A,B,C的对边为a,b,c,且 .
(1)求 ;
(2)若 的面积为 ,求内角A的角平分线 长的最大值.
【解析】(1)由正弦定理,得 ,即 ,
故 ,
因为 ,所以 ,
所以 ;
(2)由(1)知 ,
因为 的面积为 ,所以 ,解得 ,
在 中,由正弦定理,得 ,
在 中,由正弦定理,得 ,
因为AD为角A的角平分线,所以 ,
又 ,所以 ,所以 ,
不妨设 , ,则 ,故 ,
延长 至点E,使得 ,连接 ,则 ,又 ,
所以 ,故 , ,
则 , ,
则 , ,
在 中,由余弦定理,得 ,
即 ,
因为 ,所以 ,
其中 ,当且仅当 ,即 时,等号成立,
故 ,故 .
所以 长的最大值为 .