文档内容
机密★启用前
海口市 2023~2024 学年第二学期高一年级期末考试(数学)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
.
1 若集合 , ,则 ( )
A. B. C. D.
2. 复数z= (其中i是虚数单位),则z的共轭复数 =( )
A. B. C. D.
3. 已知向量 , ,若 与 共线,则 ( )
A. 3 B. C. D.
4. 已知角 的始边与 轴的非负半轴重合,终边经过点 ,则 ( )
A. B. C. D.
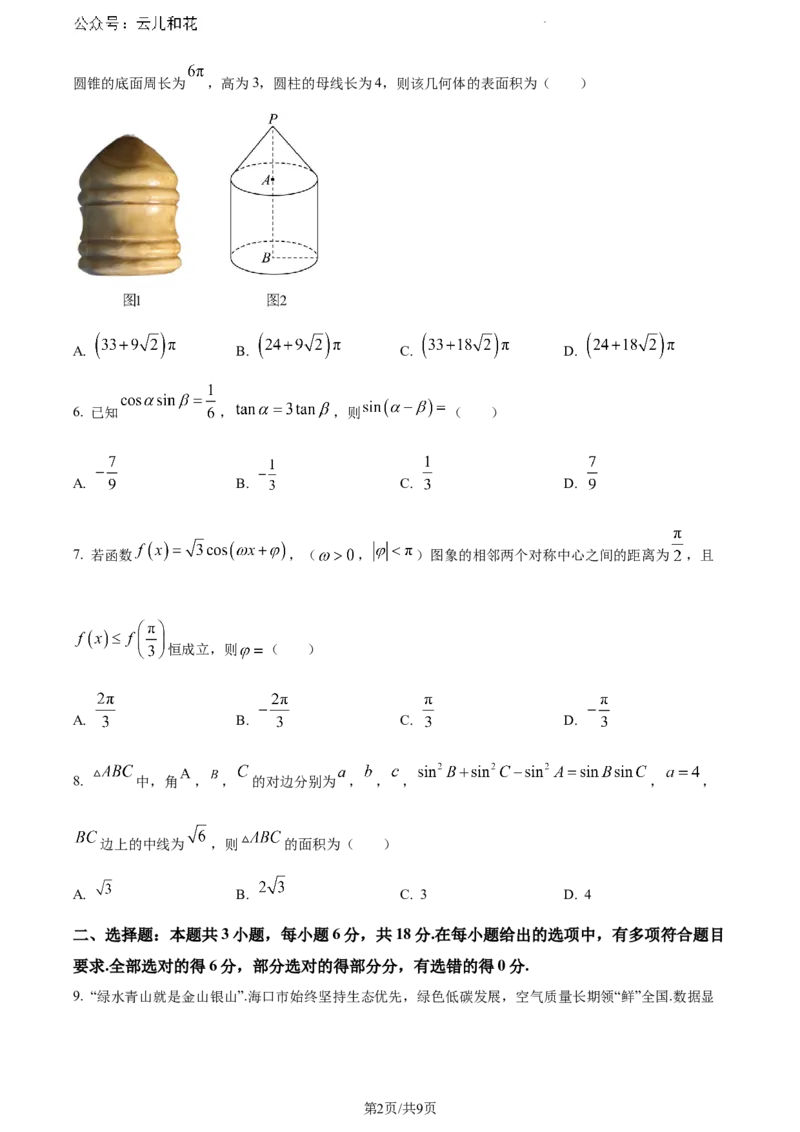
5. 陀螺是中国民间较早的娱乐工具之一,它可以近似地视为由一个圆锥和一个圆柱组合而成的几何体,如
图1是一种木陀螺,其直观图如图2所示, 为圆锥的顶点, , 分别为圆柱上、下底面圆的圆心,若
第1页/共9页
学科网(北京)股份有限公司圆锥的底面周长为 ,高为3,圆柱的母线长为4,则该几何体的表面积为( )
A. B. C. D.
6. 已知 , ,则 ( )
A. B. C. D.
7. 若函数 ,( , )图象的相邻两个对称中心之间的距离为 ,且
恒成立,则 ( )
A. B. C. D.
8. 中,角 , , 的对边分别为 , , , , ,
边上的中线为 ,则 的面积为( )
A. B. C. 3 D. 4
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. “绿水青山就是金山银山”.海口市始终坚持生态优先,绿色低碳发展,空气质量长期领“鲜”全国.数据显
第2页/共9页
学科网(北京)股份有限公司示,2023年海口市空气质量创历史最高水平,位居全国168个重点城市之首.生活中常用空气质量指数
(AQI)描述空气质量,AQI越小,表示空气质量越好.下表为2024年3月18日~3月24日一周内海口市
的
和同为空气质量排行榜前十 “某市”的空气质量指数(AQI),这组数据中,以下表述正确的是( )
A. 海口市这一周AQI的平均数为22
B. “某市”这一周AQI的中位数为40
C. 两市这一周AQI指数的方差或标准差可以反映出两市空气质量变化的稳定情况
D. 海口市这一周AQI指数的方差大于“某市”这一周AQI指数的方差
10. 设函数 , ,下列关于 和 的性质,正确的是( )
A. 对任意的 , ,
B. 对任意的 , 且 ,
C. 函数 是定义域为 的奇函数
D. 函数 在定义域上 是增函数
11. 如图,棱长为1的正方体 中,点 , , 分别为棱 , , 的中点,
点 为棱 上的动点,点 为侧面 内动点, 与侧面 成角为 ,则下列说法中正
确的是( )
第3页/共9页
学科网(北京)股份有限公司A. 动点 所在轨迹长为
B. 平面 平面
C. 平面 截正方体所得的截面图形始终是四边形
D. 点 和点 到平面 的距离相等
三、填空题:本题共3小题,每小题5分,第14题第一问2分,第二问3分,共15分.
12. 复数 ( )在复平面上对应的点在第四象限, ,则 ______.
13. 平面向量 , 为单位向量,且 ,则 ______.
14. 已知三棱锥 的顶点都在球 的表面上, 平面 , 与底面 所成的角为 ,
, , 的面积为 , 所在的平面与球 的交线长为______,球 的表面
积为______.
四、解答题:本题共5小题,共77分.解答时应写出文字说明、证明过程或演算步骤.
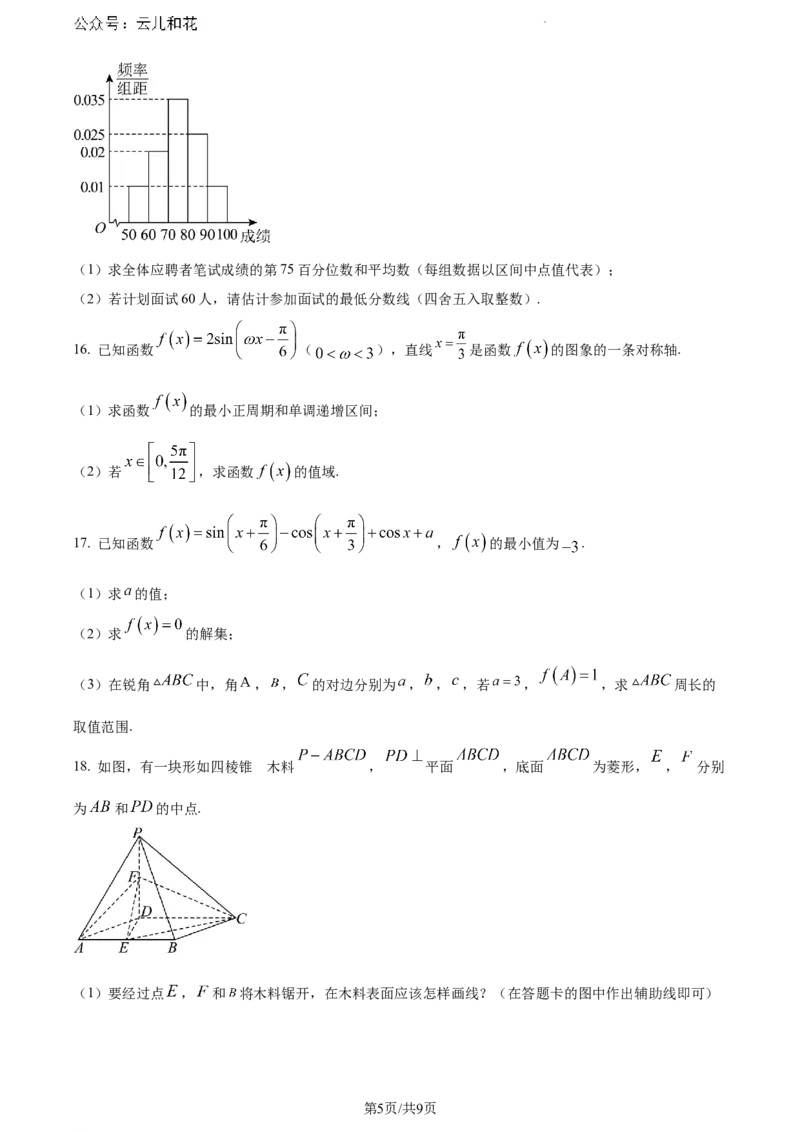
15. 为贯彻落实中央和省委相关部署要求,海口市大力开展人才引进工作.现组织公开招聘,共有100名应
聘者参加笔试,他们的笔试成绩都在 内,将笔试成绩按照 , ,…, 分
组,得到如图所示频率分布直方图.
第4页/共9页
学科网(北京)股份有限公司(1)求全体应聘者笔试成绩的第75百分位数和平均数(每组数据以区间中点值代表);
(2)若计划面试60人,请估计参加面试的最低分数线(四舍五入取整数).
16. 已知函数 ( ),直线 是函数 的图象的一条对称轴.
(1)求函数 的最小正周期和单调递增区间;
(2)若 ,求函数 的值域.
17. 已知函数 , 的最小值为 .
(1)求 的值;
(2)求 的解集;
(3)在锐角 中,角 , , 的对边分别为 , , ,若 , ,求 周长的
取值范围.
的
18. 如图,有一块形如四棱锥 木料 , 平面 ,底面 为菱形, , 分别
为 和 的中点.
(1)要经过点 , 和 将木料锯开,在木料表面应该怎样画线?(在答题卡的图中作出辅助线即可)
第5页/共9页
学科网(北京)股份有限公司指出 与平面 的位置关系,并证明;
(2)若 , , ,求二面角 的大小;
(3)试求切割开的两部分木料的体积之比.
19. 函数 称为高斯函数,其中“ ”表示不超过实数 的最大整数,又称“ 的整数部分”.高斯函数
在数论、函数绘图和计算机等领域有广泛的应用,我们记 .
(1)设方程 的两个不同实数解为 与 ,且 ,求 的值;
(2)请确认是否存在函数 : ,满足对 ,都有:
① ;② 同时成立.
(3)求证:对 , , .
第6页/共9页
学科网(北京)股份有限公司机密★启用前
海口市 2023~2024 学年第二学期高一年级期末考试(数学)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】C
【5题答案】
【答案】A
【6题答案】
【答案】C
【7题答案】
【答案】B
【8题答案】
【答案】A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】AB
【10题答案】
第7页/共9页
学科网(北京)股份有限公司【答案】AC
【11题答案】
【答案】ABD
三、填空题:本题共3小题,每小题5分,第14题第一问2分,第二问3分,共15分.
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】 ①. ②.
四、解答题:本题共5小题,共77分.解答时应写出文字说明、证明过程或演算步骤.
【15题答案】
为
【答案】(1)第 百分位数 ,平均数为
(2)
【16题答案】
【答案】(1)最小正周期为 ,单调递增区间为
(2)
【17题答案】
【答案】(1)
(2) 或
(3)
【18题答案】
【答案】(1)作图见解析, 平面 ,证明见解析
第8页/共9页
学科网(北京)股份有限公司(2)
(3) (或 )
【19题答案】
【答案】(1)
(2)不存在 (3)证明见解析
第9页/共9页
学科网(北京)股份有限公司