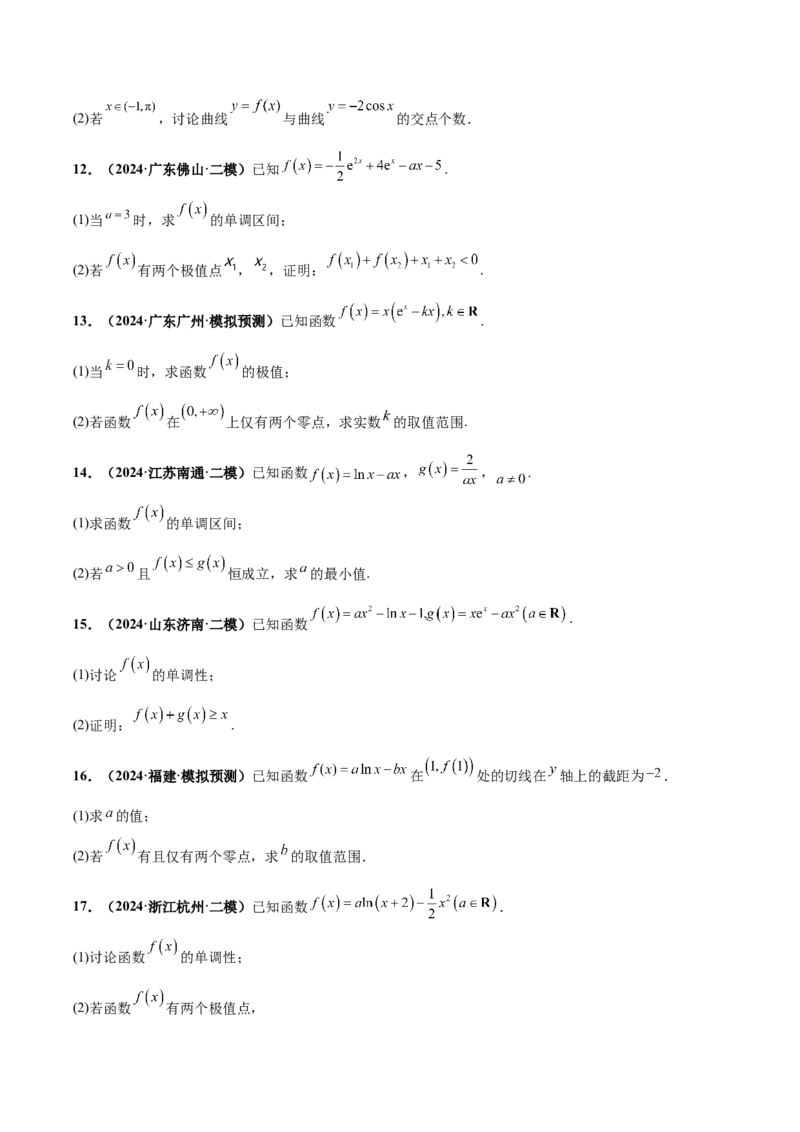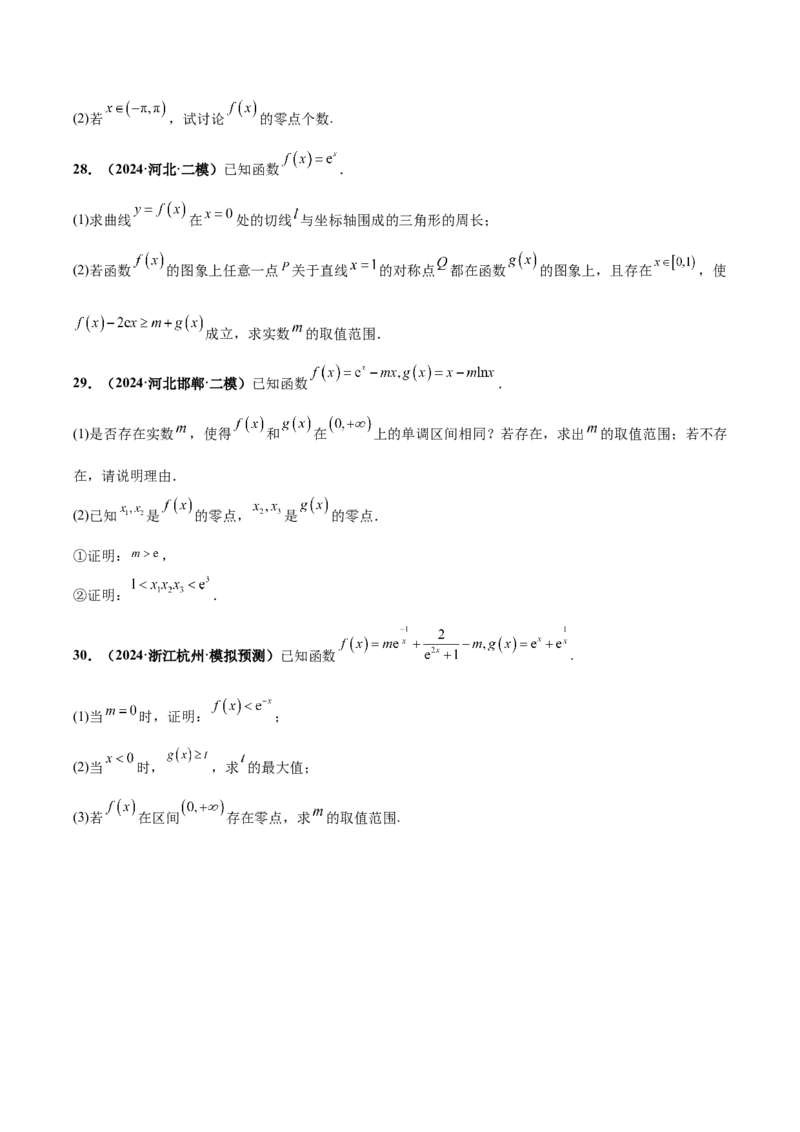文档内容
黄金冲刺大题05 导数(精选30题)
1.(2024·安徽·二模)已知函数 .
(1)求函数 在点 处的切线方程;
(2)求 的单调区间和极值.
2.(2024·江苏南京·二模)已知函数 ,其中 .
(1)当 时,求曲线 在 处的切线方程;
(2)当 时,若 在区间 上的最小值为 ,求a的值.
3.(2024·浙江绍兴·模拟预测)已知 , .
(1)讨论 的单调性.
(2)若 使得 ,求参数 的取值范围.
4.(2024·福建漳州·一模)已知函数 , 且 .
(1)证明:曲线 在点 处的切线方程过坐标原点.
(2)讨论函数 的单调性.
5.(2024·山东·二模)已知函数 .
(1)当 时,求 的单调区间;
(2)当 时, ,求 的取值范围.
6.(2024·山东·一模)已知函数 .
(1)当 时,求函数 的单调区间;(2)若函数 有两个极值点 ,且 ,求a的取值范围.
7.(2024·湖北·二模)求解下列问题,
(1)若 恒成立,求实数k的最小值;
(2)已知a,b为正实数, ,求函数 的极值.
8.(2024·湖北武汉·模拟预测)函数
.
(1)求函数 的极值;
(2)若 恒成立,求 的最大值.
9.(2024·湖北·模拟预测)已知函数 , ,
(1)若对定义域内任意非零实数 , ,均有 ,求a;
(2)记 ,证明: .
10.(2024·湖南·一模)已知函数 .
(1)当 时,求函数 在 处的切线方程;
(2) 时;
(ⅰ)若 ,求 的取值范围;
(ⅱ)证明: .
11.(2024·全国·模拟预测)已知函数 .
(1)求曲线 在 处的切线方程;(2)若 ,讨论曲线 与曲线 的交点个数.
12.(2024·广东佛山·二模)已知 .
(1)当 时,求 的单调区间;
(2)若 有两个极值点 , ,证明: .
13.(2024·广东广州·模拟预测)已知函数 .
(1)当 时,求函数 的极值;
(2)若函数 在 上仅有两个零点,求实数 的取值范围.
14.(2024·江苏南通·二模)已知函数 , , .
(1)求函数 的单调区间;
(2)若 且 恒成立,求 的最小值.
15.(2024·山东济南·二模)已知函数
(1)讨论 的单调性;
(2)证明: .
16.(2024·福建·模拟预测)已知函数 在 处的切线在 轴上的截距为 .
(1)求 的值;
(2)若 有且仅有两个零点,求 的取值范围.
17.(2024·浙江杭州·二模)已知函数 .
(1)讨论函数 的单调性;
(2)若函数 有两个极值点,(ⅰ)求实数 的取值范围;
(ⅱ)证明:函数 有且只有一个零点.
18.(2024·河北沧州·模拟预测)已知函数 , .
(1)讨论 的单调性;
(2)若 , 恒成立,求实数a的取值范围.
19.(2024·广东·二模)已知 .
(1)求 的单调区间;
(2)函数 的图象上是否存在两点 (其中 ),使得直线 与函数 的图象
在 处的切线平行?若存在,请求出直线 ;若不存在,请说明理由.
20.(2024·广东深圳·二模)已知函数 , 是 的导函数,且 .
(1)若曲线 在 处的切线为 ,求k,b的值;
(2)在(1)的条件下,证明: .
21.(2024·辽宁·二模)已知函数 .
(1)若曲线 在 处的切线方程为 ,求实数 的值;
(2)若对于任意 , 恒成立,求实数 的取值范围.
22.(2024·黑龙江哈尔滨·一模)已知函数 .
(1)当 时,求 在 处的切线方程;
(2)当 时,求 的单调区间和极值;(3)若对任意 ,有 恒成立,求 的取值范围.
23.(2024·安徽合肥·二模)已知曲线 在点 处的切线为 .
(1)求直线 的方程;
(2)证明:除点 外,曲线 在直线 的下方;
(3)设 ,求证: .
24.(2024·江苏扬州·模拟预测)已知函数 .
(1)讨论函数 的单调性;
(2)若存在正数 ,使 成立,求 的取值范围;
(3)若 ,证明:对任意 ,存在唯一的实数 ,使得 成立.
25.(2024·重庆·模拟预测)已知函数
(1)若过点 的直线与曲线 切于点 ,求 的值;
(2)若 有唯一零点,求 的取值范围.
26.(2024·江苏南通·模拟预测)设函数 , .
(1)若 ,求函数 的单调区间;
(2)若 ,试判断函数 在区间 内的极值点的个数,并说明理由;
(3)求证:对任意的正数 ,都存在实数 ,满足:对任意的 , .
27.(2024·河北保定·二模)已知函数 .
(1)若 ,求曲线 在点 处的切线方程;(2)若 ,试讨论 的零点个数.
28.(2024·河北·二模)已知函数 .
(1)求曲线 在 处的切线 与坐标轴围成的三角形的周长;
(2)若函数 的图象上任意一点 关于直线 的对称点 都在函数 的图象上,且存在 ,使
成立,求实数 的取值范围.
29.(2024·河北邯郸·二模)已知函数 .
(1)是否存在实数 ,使得 和 在 上的单调区间相同?若存在,求出 的取值范围;若不存
在,请说明理由.
(2)已知 是 的零点, 是 的零点.
①证明: ,
②证明: .
30.(2024·浙江杭州·模拟预测)已知函数 .
(1)当 时,证明: ;
(2)当 时, ,求 的最大值;
(3)若 在区间 存在零点,求 的取值范围.