文档内容
黄金冲刺大题03 立体几何
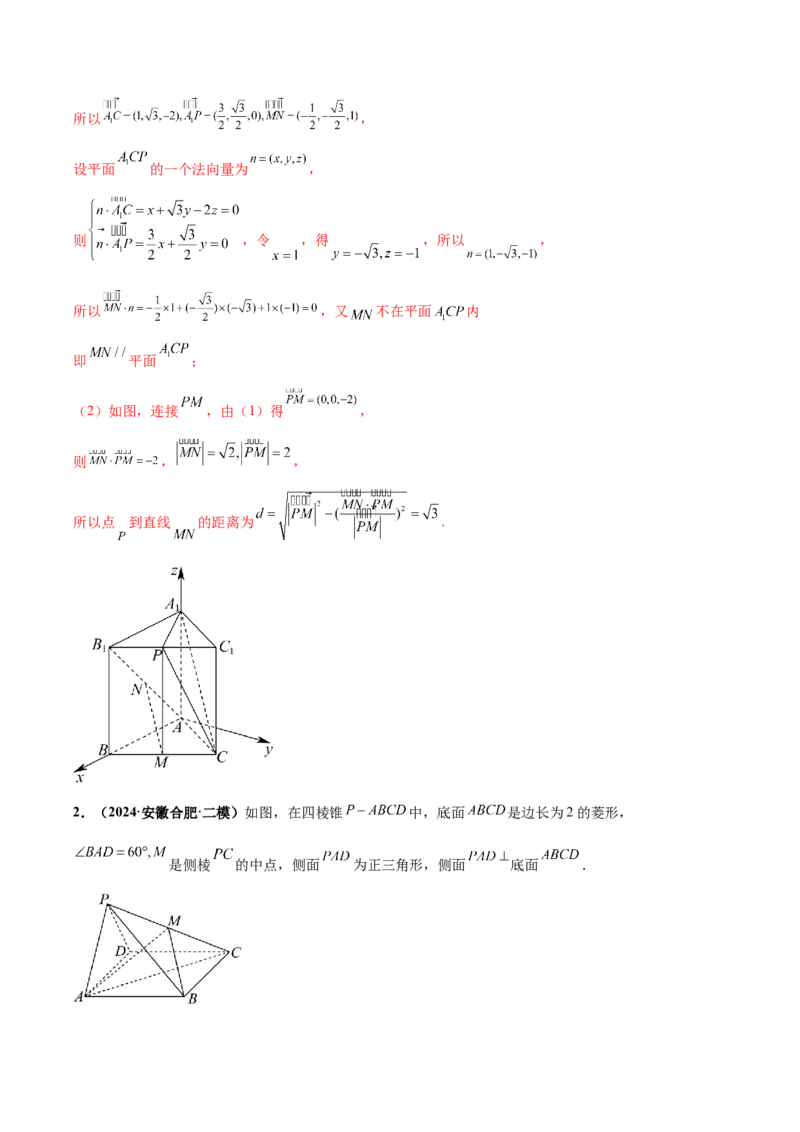
1.(2024·黑龙江·二模)如图,已知正三棱柱 的侧棱长和底面边长均为2,M是BC的中点,
N是 的中点,P是 的中点.
(1)证明: 平面 ;
(2)求点P到直线MN的距离.
【答案】(1)证明见解析
(2)
【分析】(1)建立如图空间直角坐标系 ,设平面 的一个法向量为 ,利用空间向量
法证明 即可;
(2)利用空间向量法即可求解点线距.
【详解】(1)由题意知, 平面 , ,而 平面 ,
所以 ,在平面 内过点A作y轴,使得 y轴,
建立如图空间直角坐标系 ,
则 ,得 ,所以 ,
设平面 的一个法向量为 ,
则 ,令 ,得 ,所以 ,
所以 ,又 不在平面 内
即 平面 ;
(2)如图,连接 ,由(1)得 ,
则 , ,
所以点 到直线 的距离为 .
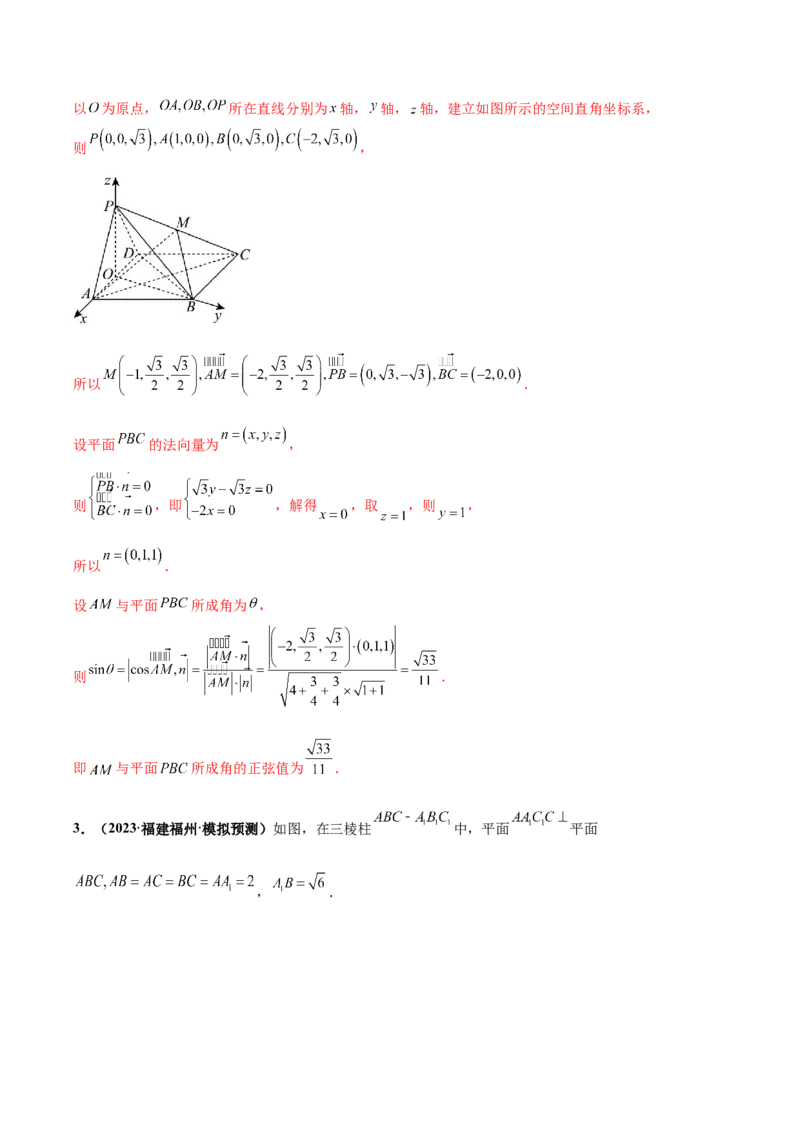
2.(2024·安徽合肥·二模)如图,在四棱锥 中,底面 是边长为2的菱形,
是侧棱 的中点,侧面 为正三角形,侧面 底面 .(1)求三棱锥 的体积;
(2)求 与平面 所成角的正弦值.
【答案】(1)
(2) .
【分析】(1)作出辅助线,得到线线垂直,进而得到线面垂直,由中位线得到 到平面 的距离为
,进而由锥体体积公式求出答案;
(2)证明出 ,建立空间直角坐标系,求出平面的法向量,进而由法向量的夹角余弦值的绝对值
求出线面角的正弦值.
【详解】(1)如图所示,取 的中点 ,连接 .
因为 是正三角形,所以 .
又因为平面 底面 平面 ,平面 平面 ,
所以 平面 ,且 .
又因为 是 的中点, 到平面 的距离为 ,
,
所以三棱锥 的体积为 .
(2)连接 ,因为 ,
所以 为等边三角形,所以 ,以 为原点, 所在直线分别为 轴, 轴, 轴,建立如图所示的空间直角坐标系,
则 ,
所以 .
设平面 的法向量为 ,
则 ,即 ,解得 ,取 ,则 ,
所以 .
设 与平面 所成角为 ,
则 .
即 与平面 所成角的正弦值为 .
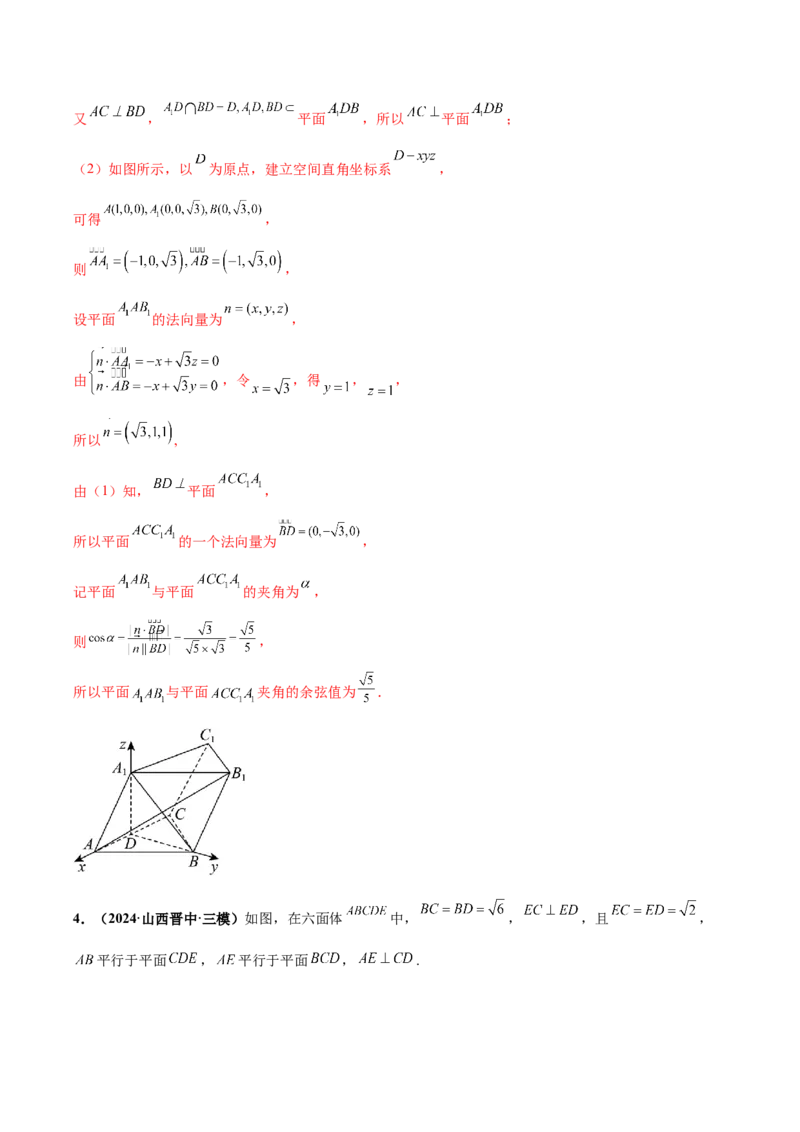
3.(2023·福建福州·模拟预测)如图,在三棱柱 中,平面 平面
, .(1)设 为 中点,证明: 平面 ;
(2)求平面 与平面 夹角的余弦值.
【答案】(1)证明见解析;
(2)
【分析】(1)根据等边三角形的性质得出 ,根据平面 平面 得出 平面
, ,利用勾股定理得出 ,从而证明 平面 ;
(2)建立空间直角坐标系,利用坐标表示向量,求出平面 的法向量和平面 的一个法向量,
利用向量求平面 与平面 的夹角余弦值.
【详解】(1)证明:因为 为 中点,且 ,
所以在 中,有 ,且 ,
又平面 平面 ,且平面 平面 , 平面 ,
所以 平面 ,
又 平面 ,则 ,
由 , ,得 ,
因为 , , ,所以由勾股定理,得 ,又 , 平面 ,所以 平面 ;
(2)如图所示,以 为原点,建立空间直角坐标系 ,
可得 ,
则 ,
设平面 的法向量为 ,
由 ,令 ,得 , ,
所以 ,
由(1)知, 平面 ,
所以平面 的一个法向量为 ,
记平面 与平面 的夹角为 ,
则 ,
所以平面 与平面 夹角的余弦值为 .
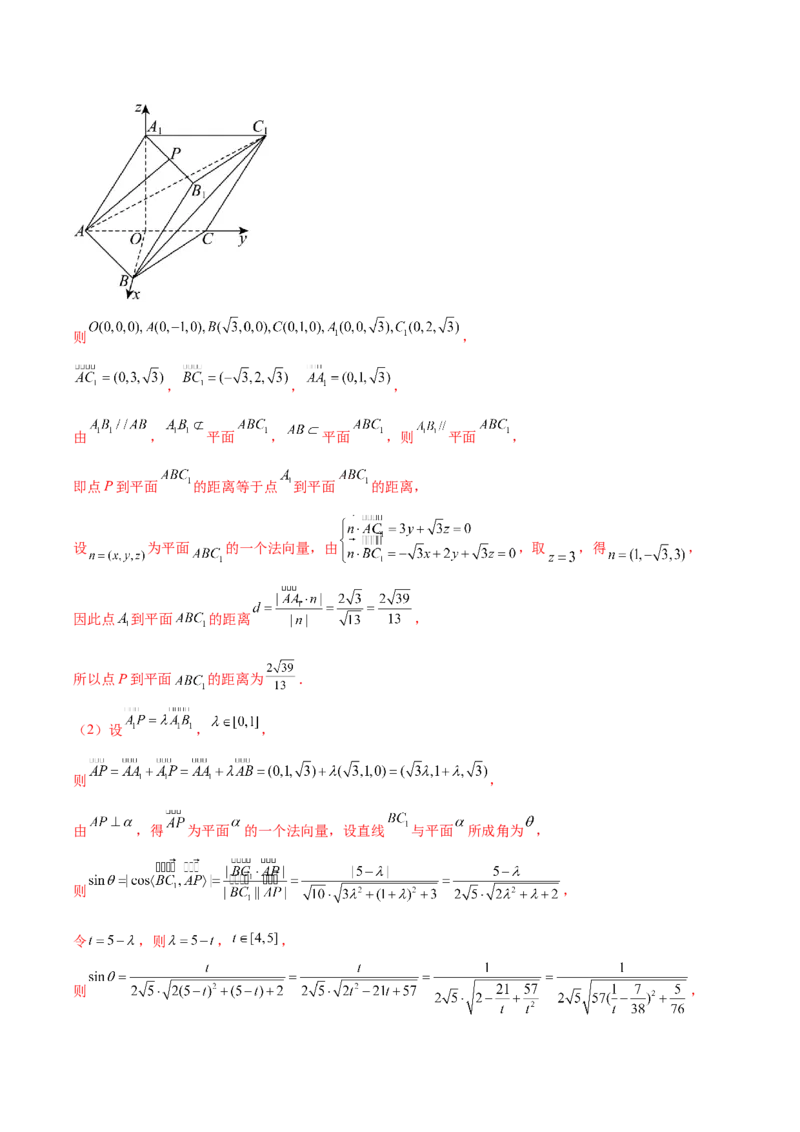
4.(2024·山西晋中·三模)如图,在六面体 中, , ,且 ,
平行于平面 , 平行于平面 , .(1)证明:平面 平面 ;
(2)若点 到直线 的距离为 , 为棱 的中点,求平面 与平面 夹角的余弦值.
【答案】(1)证明见解析
(2)
【分析】(1)设平面 与直线 交于点 ,使用线面平行的性质,然后用面面垂直的判定定理即可;
(2)证明 平面 ,然后构造空间直角坐标系,直接用空间向量方法即可得出结果.
【详解】(1)设平面 与直线 交于点 ,连接 ,则平面 与平面 的交线为 ,
平面 与平面 的交线为 ,因为 平行于平面 , 平面 ,平面 和平面 的
交线为 ,所以 .同理 ,所以四边形 是平行四边形,故 , .
因为 , ,所以 ,又 ,所以 为棱 的中点
在 中, , ,所以 ,由于 ,故 .
而 , , 平面 ,所以 平面 ,
又 平面 ,所以平面 平面
(2)由(1)可知, 平面 ,又 平面 ,所以 .
而点 到直线 的距离为 ,故 .
在等腰直角三角形 中,由 得
在等腰三角形 中,由 , ,得 .
在平行四边形 中, , , ,由余弦定理得 ,
所以 ,所以 .
因为 ,所以 .
因为平面 平面 ,平面 和平面 的交线为 , 在平面 内.
所以 平面
如图,以 为坐标原点, 分别为 轴正方向,建立空间直角坐标系.
则 .
所以
设平面 的法向量为 ,则 ,即 .
则可取 ,得 .
设平面 的法向量为 ,则 ,即 .
取 ,则 .设平面 与平面 的夹角为 ,则 .
所以平面 与平面 夹角的余弦值为
5.(2024·辽宁·二模)棱长均为2的斜三棱柱 中, 在平面ABC内的射影O在棱AC的中点
处,P为棱 (包含端点)上的动点.
(1)求点P到平面 的距离;
(2)若 平面 ,求直线 与平面 所成角的正弦值的取值范围.
【答案】(1) ;
(2) .
【分析】(1)以O为原点建立空间直角坐标系,求出平面 的法向量,再利用点到平面距离的向量求
法求解即得.
(2)由向量共线求出向量 的坐标,再利用线面角的向量求法列出函数关系,并求出函数的值域即可.
【详解】(1)依题意, 平面ABC, (底面为正三角形),且 ,
以O为原点, 的方向分别为 轴的正方向,建立空间直角坐标系,如图,则 ,
, , ,
由 , 平面 , 平面 ,则 平面 ,
即点P到平面 的距离等于点 到平面 的距离,
设 为平面 的一个法向量,由 ,取 ,得 ,
因此点 到平面 的距离 ,
所以点P到平面 的距离为 .
(2)设 , ,
则 ,
由 ,得 为平面 的一个法向量,设直线 与平面 所成角为 ,
则 ,
令 ,则 , ,
则 ,由 ,得 ,于是 , ,则
,
所以直线 与平面 所成角的正弦值的取值范围是 .
6.(2024·重庆·模拟预测)在如图所示的四棱锥P ABCD中,已知 , , ,
是正三角形,点M在侧棱PB上且使得 平面 .
(1)证明: ;
(2)若侧面 底面 , 与底面 所成角的正切值为 ,求二面角 的余弦值.
【答案】(1)证明见解析;
(2) .
【分析】(1)连接BD与AC交于点E,连接EM,由已知得 ,由线面平行的性质得 ,
根据三角形相似可得 ,即
(2)设AB的中点O,首先由已知得 底面ABCD,在 中过点M作 交AB于点F,得
底面ABCD,则 为CM与底面ABCD所成角,在底面ABCD上过点O作 于点G,则
是二面角 的平面角,根据条件求解即可
【详解】(1)证明:连接BD与AC交于点E,连接EM,
在 与 中,∵ ,∴ ,由 ,得 ,又∵ 平面AMC,
而平面 平面 , 平面PBD,
∴ ,
∴在 中, ,∴ ;
(2)设AB的中点O,在正 中, ,
而侧面 底面 ,侧面 底面 ,且 平面 ,
∴ 底面ABCD,
在 中过点M作 交AB于点F,
∴ 底面ABCD,
∴ 为CM与底面ABCD所成角,
∴ ,设 ,
则 ,∴ , ,则在直角梯形ABCD中, ,
而 ,则 ,
在底面ABCD上过点O作 于点G,
则 是二面角 的平面角,易得 , ,在梯形ABCD中,由 ,得 ,
在 中, ,∴ .
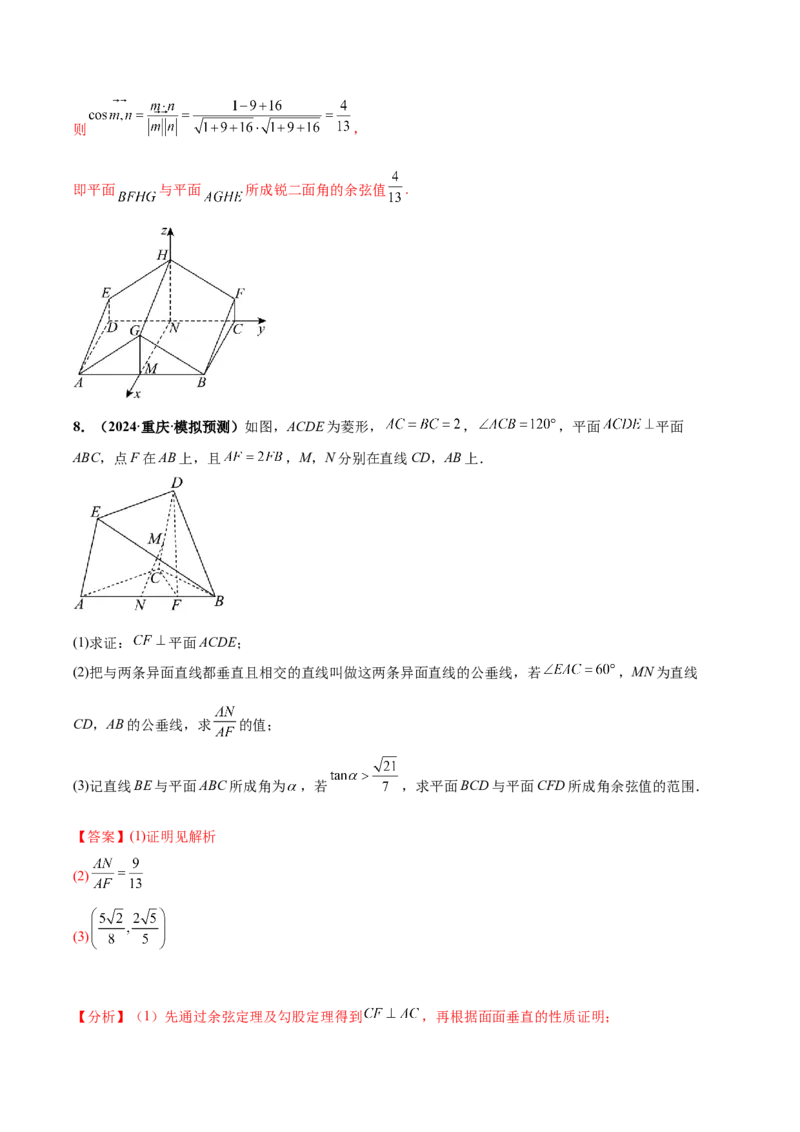
7.(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对
“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示
的七面体 是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形, m,
m, m,且ED,CF都垂直于平面ABCD, m, ,平面 平面
ABCD.
(1)求点H到平面ABCD的距离;
(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.
【答案】(1)
(2)
【分析】(1)取 的中点 ,证得平面 平面 ,得到 ,再由平面
平面 ,证得 ,得到平行四边形 ,得到 ,求得 ,结合 平面
,即可求解;
(2)以点 为原点,建立空间直角坐标系,分别求得平面 和平面 的法向量
和 ,结合向量的夹角公式,即可求解.
【详解】(1)如图所示,取 的中点 ,连接 ,
因为 ,可得 ,又因为平面 平面 ,且平面 平面 , 平面 ,
所以 平面 ,同理可得: 平面 ,
因为 平面 ,所以 ,
又因为 平面 , 平面 ,所以 平面 ,
因为 ,且 平面 , 平面 ,所以 平面 ,
又因为 ,且 平面 ,所以平面 平面 ,
因为平面 与平面 和平面 于 ,可得 ,
又由 , ,且 和 ,
所以平面 平面 ,
因为平面 与平面 和平面 于 ,所以 ,
可得四边形 为平行四边形,所以 ,
因为 ,所以 ,
在直角 ,可得 ,
在直角梯形 中,可得 ,
因为 平面 ,所以点 到平面 的距离为 .
(2)解:以点 为原点,以 所在的直线分别为 轴,建立空间直角坐标系,
如图所示,则 ,
可得 ,
设平面 的法向量为 ,则 ,
取 ,可得 ,所以 ,
设平面 的法向量为 ,则 ,
取 ,可得 ,所以 ,则 ,
即平面 与平面 所成锐二面角的余弦值 .
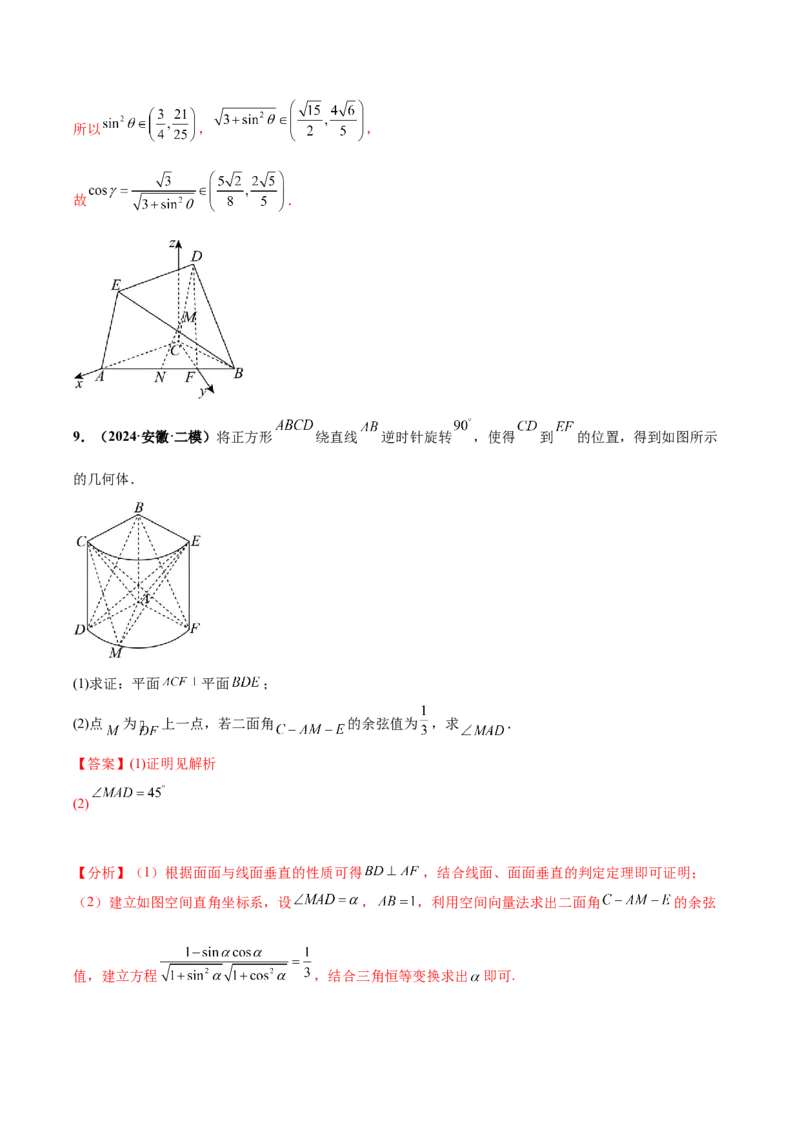
8.(2024·重庆·模拟预测)如图,ACDE为菱形, , ,平面 平面
ABC,点F在AB上,且 ,M,N分别在直线CD,AB上.
(1)求证: 平面ACDE;
(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若 ,MN为直线
CD,AB的公垂线,求 的值;
(3)记直线BE与平面ABC所成角为 ,若 ,求平面BCD与平面CFD所成角余弦值的范围.
【答案】(1)证明见解析
(2)
(3)
【分析】(1)先通过余弦定理及勾股定理得到 ,再根据面面垂直的性质证明;(2)以C为原点,CA的方向为x轴正方向,建立如图所示空间直角坐标系 ,利用向量的坐标运算
根据 ,列方程求解即可;
(3)利用向量法求面面角,然后根据 列不等式求解.
【详解】(1) , ,
所以 , , ,
,则 ,
又因为平面 平面ABC,平面 平面 面 ,
故 平面ACDE;
(2)以C为原点,CA的方向为x轴正方向,建立如图所示空间直角坐标系 ,
由 ,可得 , ,
所以
所以 , ,
设 ,则 ,
设 ,则 , ,
由题知, ,解得 , ,故 ;
(3) ,设 ,
则 , ,
可取平面ABC的法向量 ,
则 ,
,
则 ,
整理得 ,故 ,
, , ,
记平面CDF的法向量为 ,则有 ,
可得 ,
记平面CBD的法向量为 ,则有 ,
可得 ,
记平面BCD与平面CFD所成角为 ,
则 , ,所以 , ,
故 .
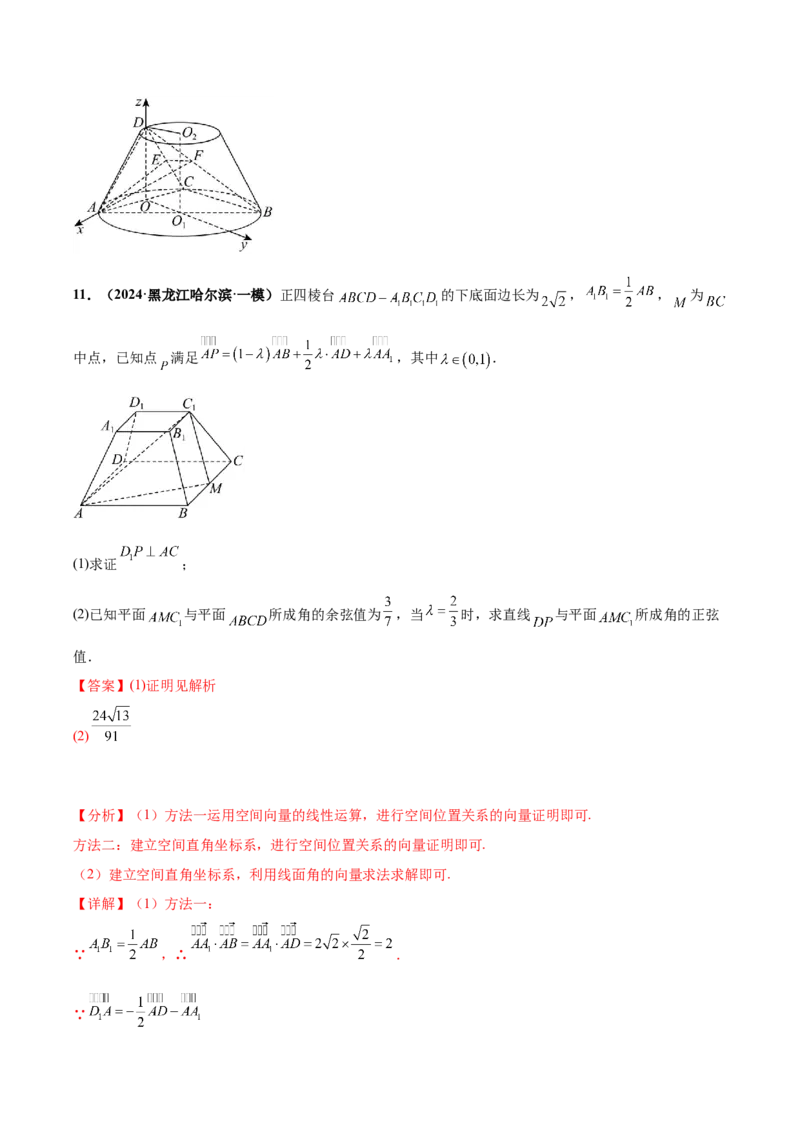
9.(2024·安徽·二模)将正方形 绕直线 逆时针旋转 ,使得 到 的位置,得到如图所示
的几何体.
(1)求证:平面 平面 ;
(2)点 为 上一点,若二面角 的余弦值为 ,求 .
【答案】(1)证明见解析
(2)
【分析】(1)根据面面与线面垂直的性质可得 ,结合线面、面面垂直的判定定理即可证明;
(2)建立如图空间直角坐标系,设 , ,利用空间向量法求出二面角 的余弦
值,建立方程 ,结合三角恒等变换求出 即可.【详解】(1)由已知得平面 平面 , ,平面 平面 , 平面
,
所以 平面 ,又 平面 ,故 ,
因为 是正方形,所以 ,
, 平面 , ,所以 平面 ,
又 平面 ,所以平面 平面 .
(2)由(1)知 , , 两两垂直,
以 , , 所在直线分别为 , , 轴,建立空间直角坐标系,如图.
设 , ,
则 , , , ,
故 , ,
设平面 的法向量为 ,则 ,
故 ,取 ,则 ,
所以
设平面 的法向量为 , ,
故 ,取 ,则 ,
所以 ,所以 ,
由已知得 ,
化简得: ,解得 或 (舍去)
故 ,即 .
10.(2024·安徽黄山·二模)如图,已知 为圆台下底面圆 的直径, 是圆 上异于 的点, 是
圆台上底面圆 上的点,且平面 平面 , , , 是 的中点,
.
(1)证明: ;
(2)求直线 与平面 所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】(1)取AC的中点O,根据面面垂直的性质定理,可得 平面 ,即可求证 ,
进而可证矩形,即可根据线线平行以及平行的传递性求解.
(2)建系,利用向量法,求解法向量 与方向向量 的夹角,即可求解.
【详解】(1)证明:取 的中点为 ,连接 , , ,, 为 中点, ,
又平面 平面 ,且平面 平面 , 平面 ,
平面 , , ,故四边形 为矩形,
,又 , 分别是 , 的中点,
,
;
(2) 是圆 上异于 , 的点,且 为圆 的直径,
, ,
如图以 为原点建立空间直角坐标系,由条件知 ,
,0, , ,4, , ,0, , , ,
设 , , , , ,
由 ,得 , ,
, ,
设平面 法向量为 ,
则 ,取 ,
设直线 与平面 所成角为 ,
则
直线 与平面 所成角的正弦值为 .11.(2024·黑龙江哈尔滨·一模)正四棱台 的下底面边长为 , , 为
中点,已知点 满足 ,其中 .
(1)求证 ;
(2)已知平面 与平面 所成角的余弦值为 ,当 时,求直线 与平面 所成角的正弦
值.
【答案】(1)证明见解析
(2)
【分析】(1)方法一运用空间向量的线性运算,进行空间位置关系的向量证明即可.
方法二:建立空间直角坐标系,进行空间位置关系的向量证明即可.
(2)建立空间直角坐标系,利用线面角的向量求法求解即可.
【详解】(1)方法一:
∵ ,∴ .
∵∴
∴
.
∴ ,即 .
方法二:以底面ABCD的中心O为原点,以OM方向为y轴,过O点平行于AD向前方向为x轴,
以过点O垂直平面ABCD向上方向为z轴,建立如图所示空间直角坐标系,设正四棱台的高度为h,则有
, , ,
, , ,
, ,
,
.
故 ,所以 .
(2)设平面ABCD的法向量为 ,设平面 的法向量为 , , ,
则有 ,即 ,
令 ,则 .
又题意可得 ,可得 .
因为 ,经过计算可得 , , .
将 代入,可得平面 的法向量 .
设直线DP与平面 所成角的为θ
.
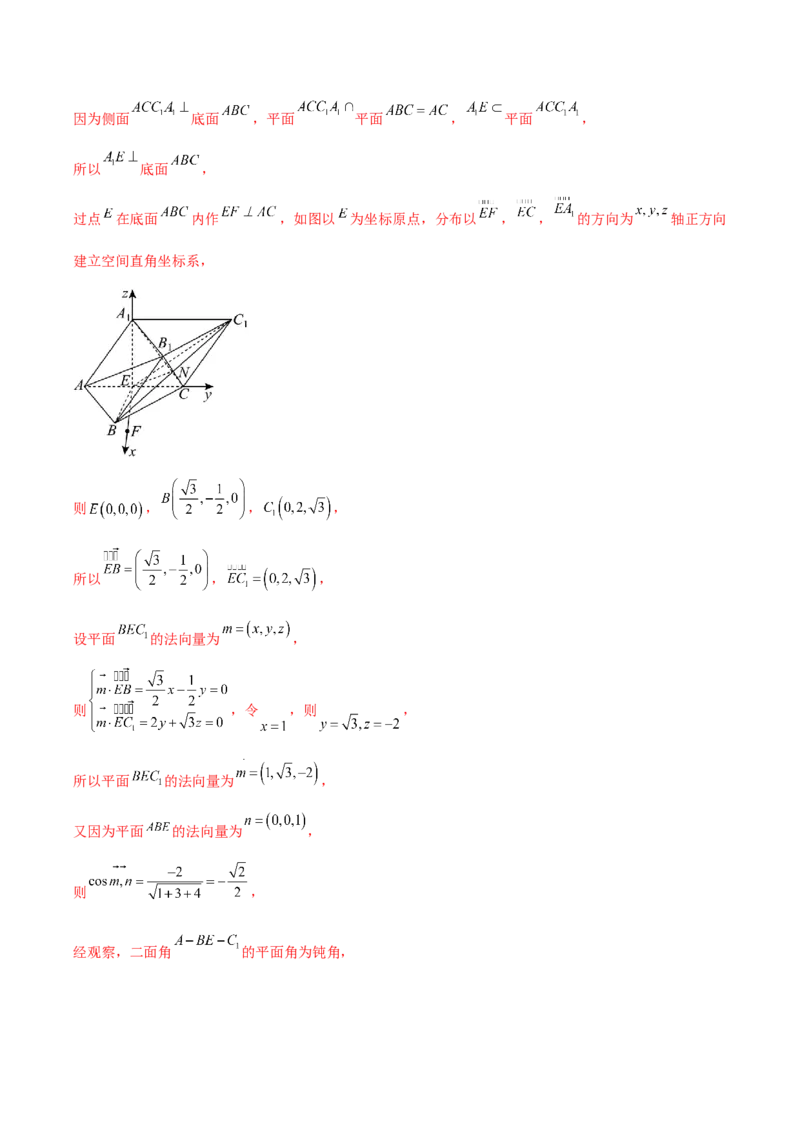
12.(2024·辽宁·三模)如图,在三棱柱 中,侧面 底面 ,
,点 为线段 的中点.
(1)求证: 平面 ;
(2)若 ,求二面角 的余弦值.【答案】(1)证明见详解
(2)
【分析】(1)连接 ,交 于点 ,连接 ,利用线面平行的判定定理证明;
(2)由已知可知, 为等边三角形,故 ,利用面面垂直的性质定理可证得 底面
,进而建立空间直角坐标系,利用向量法即可求二面角余弦值.
【详解】(1)连接 ,交 于点 ,连接 ,
因为侧面 是平行四边形,
所以 为 的中点,又因为点 为线段 的中点,
所以 ,
因为 面 , 面 ,
所以 面 .
(2)连接 , ,因为 , ,
所以 为等边三角形, ,
因为点 为线段 的中点,
所以 ,因为侧面 底面 ,平面 平面 , 平面 ,
所以 底面 ,
过点 在底面 内作 ,如图以 为坐标原点,分布以 , , 的方向为 轴正方向
建立空间直角坐标系,
则 , , ,
所以 , ,
设平面 的法向量为 ,
则 ,令 ,则 ,
所以平面 的法向量为 ,
又因为平面 的法向量为 ,
则 ,
经观察,二面角 的平面角为钝角,所以二面角 的余弦值为 .
13.(2024·广东广州·一模)如图,在四棱锥 中,底面 是边长为 的菱形, 是等边
三角形, ,点 , 分别为 和 的中点.
(1)求证: 平面 ;
(2)求证:平面 平面 ;
(3)求 与平面 所成角的正弦值.
【答案】(1)证明见解析;
(2)证明见解析;
(3) .
【分析】(1)取 中点 ,由已知条件,结合线面平行的判断推理即得.
(2)过 作 于点 ,借助三角形全等,及线面垂直的判定、面面垂直的判定推理即得.
(3)建立空间直角坐标系,利用线面角的向量求法求解即得.
【详解】(1)取 中点 ,连接 ,由 为 中点, 为 中点,得 ,
又 ,则 ,因此四边形 为平行四边形,
于是 ,而 平面 平面 ,
所以 平面 .
(2)过 作 于点 ,连接 ,由 ,得 ≌ ,
则 ,即 ,而 ,
因此 ,又 平面 ,则 平面 , 平面 ,所以平面 平面 .
(3)由(2)知,直线 两两垂直,
以点 为原点,直线 分别为 轴建立空间直角坐标系,
则 ,
,
设平面 的一个法向量 ,则 ,令 ,得 ,
设 与平面 所成角为 , ,
所以 与平面 所成角的正弦值是 .
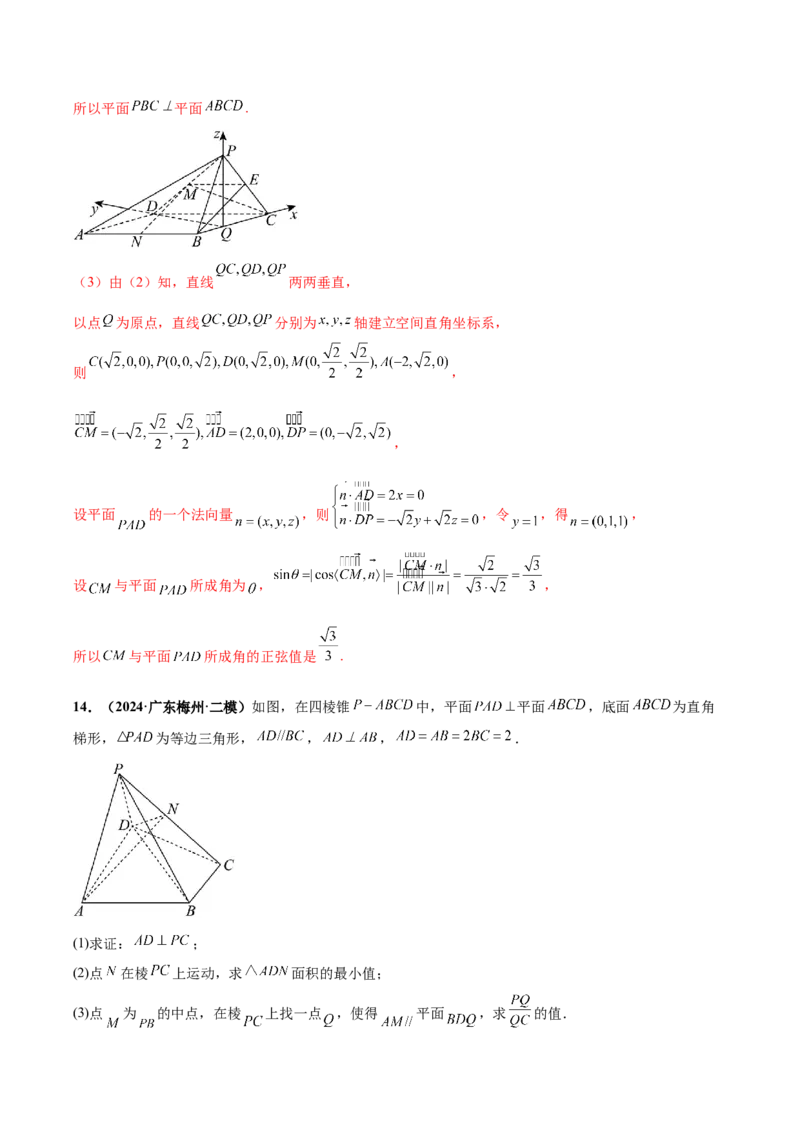
14.(2024·广东梅州·二模)如图,在四棱锥 中,平面 平面 ,底面 为直角
梯形, 为等边三角形, , , .
(1)求证: ;
(2)点 在棱 上运动,求 面积的最小值;
(3)点 为 的中点,在棱 上找一点 ,使得 平面 ,求 的值.【答案】(1)证明见解析
(2)
(3)
【分析】(1)取 的中点 ,连接 , ,依题意可得四边形 为矩形,即可证明 ,
再由 ,即可证明 平面 ,从而得证;
(2)连接 交 于点 ,连接 交 于点 ,连接 ,即可得到 ,再根据线面平行的性
质得到 ,在 中,过点 作 ,即可得到 ,最后由 即可得解.
【详解】(1)取 的中点 ,连接 , ,则 且 ,又 ,
所以四边形 为矩形,
所以 ,又 为等边三角形,
所以 , , 平面 ,
所以 平面 ,
又 平面 ,
所以 .
(2)连接 ,由 平面 ,
又 平面 ,
所以 ,所以 ,
要使 的面积最小,即要使 最小,
当且仅当 时 取最小值,
因为平面 平面 ,平面 平面 , 平面 ,所以 平面 ,
又 平面 ,所以 ,
在 中, , ,所以 ,
当 时 ,
所以 面积的最小值为 .
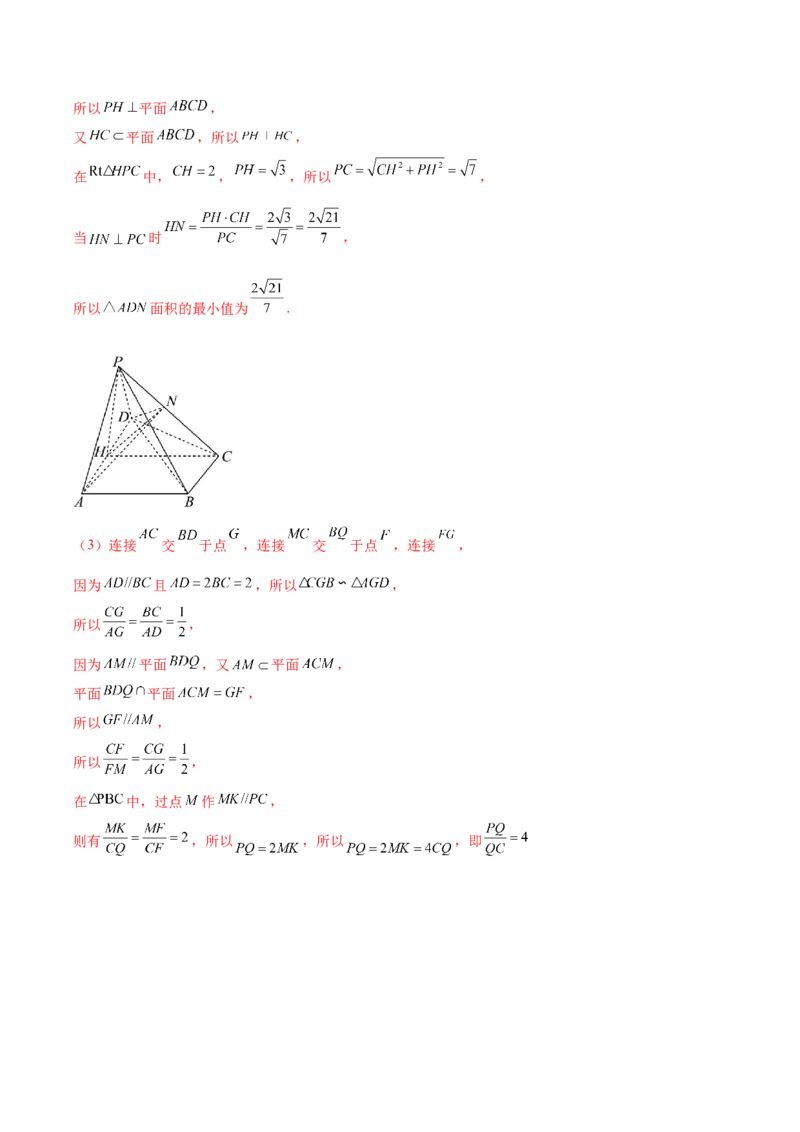
(3)连接 交 于点 ,连接 交 于点 ,连接 ,
因为 且 ,所以 ,
所以 ,
因为 平面 ,又 平面 ,
平面 平面 ,
所以 ,
所以 ,
在 中,过点 作 ,
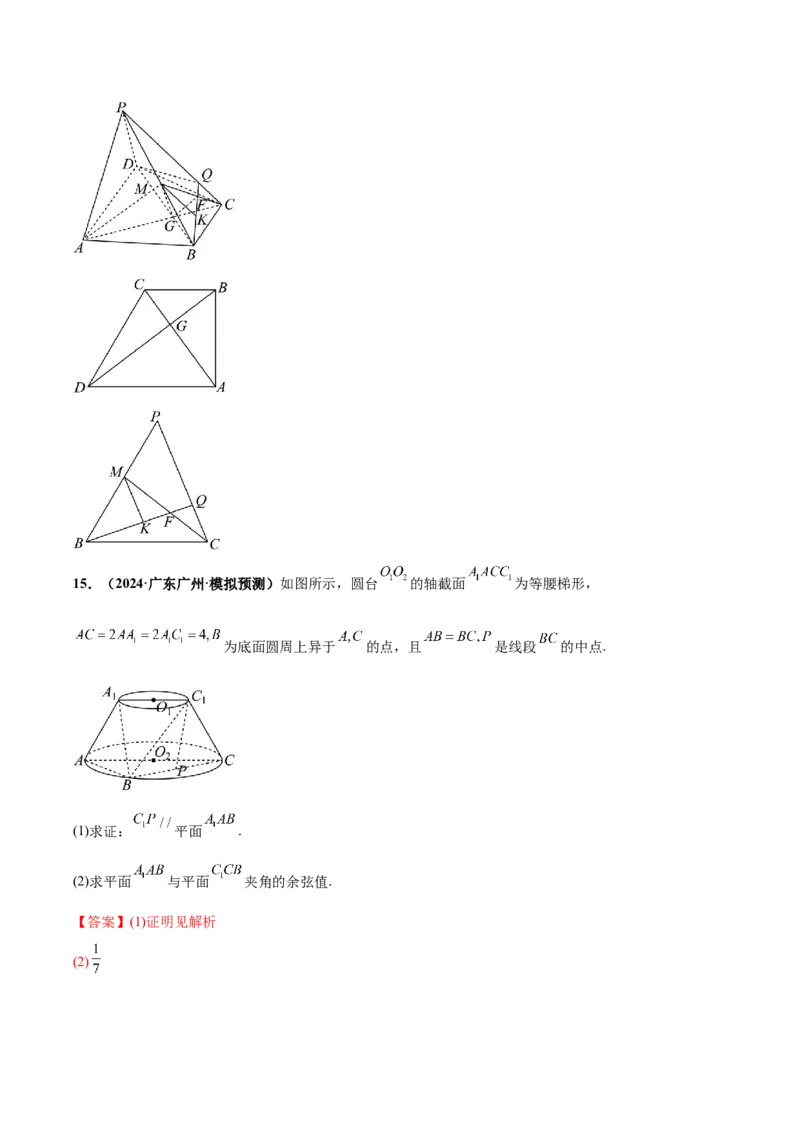
则有 ,所以 ,所以 ,即15.(2024·广东广州·模拟预测)如图所示,圆台 的轴截面 为等腰梯形,
为底面圆周上异于 的点,且 是线段 的中点.
(1)求证: 平面 .
(2)求平面 与平面 夹角的余弦值.
【答案】(1)证明见解析
(2)【分析】(1)取 的中点 ,连接 ,证明四边形 为平行四边形,进而得 ,
即可证明;
(2)建立空间直角坐标系,求两平面的法向量,利用平面夹角公式求解.
【详解】(1)取 的中点 ,连接 ,如图所示,
因为 为 的中点,所以 .
在等腰梯形 中, ,
所以 ,所以四边形 为平行四边形,
所以 ,又 平面 平面 ,
所以 平面 .
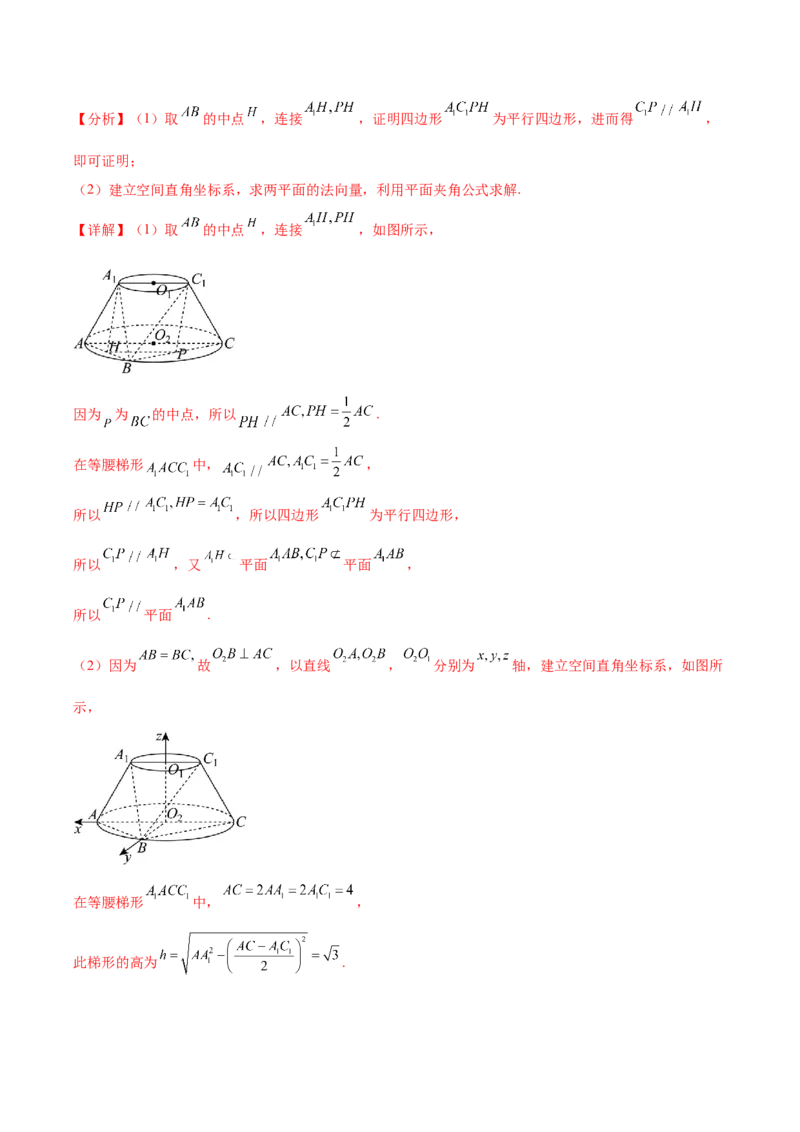
(2)因为 故 ,以直线 , 分别为 轴,建立空间直角坐标系,如图所
示,
在等腰梯形 中, ,
此梯形的高为 .因为 ,
则 ,
所以 .
设平面 的法向量为 ,则
令 ,得 .
设平面 的法向量为 ,
则 令 ,得 .
设平面 与平面 的夹角为 ,
则 .
16.(2024·广东深圳·二模)如图,三棱柱 中,侧面 底面ABC,且 ,
.
(1)证明: 平面ABC;(2)若 , ,求平面 与平面 夹角的余弦值.
【答案】(1)证明见解析;
(2) .
【分析】(1)取BC的中点M,连结MA、 ,根据等腰三角形性质和线面垂直判定定理得 平面
,进而由 得 ,再证明 平面ABC即可得证.
(2)建立空间直角坐标系,用向量法求解即可;也可用垂面法作出垂直于 的垂面,从而得出二面角的
平面角再进行求解即可.
【详解】(1)取BC的中点M,连结MA、 .
因为 , ,所以 , ,
由于AM, 平面 ,且 ,
因此 平面 ,
因为 平面 ,所以 ,
又因为 ,所以 ,
因为平面 平面ABC,平面 平面 ,且 平面 ,所以 平面
ABC,因为 ,所以 平面ABC.
(2)法一:因为 ,且 ,所以 .
以AB,AC, 所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系 ,
则 , , , .
所以 , , .
设平面 的法向量为 ,则 ,可得 ,
令 ,则 ,
设平面 的法向量为 ,则 ,可得 ,
令 ,则 ,
设平面 与平面 夹角为 ,则 ,
所以平面 与平面 夹角的余弦值为 .
法二:将直三棱柱 补成长方体 .
连接 ,过点C作 ,垂足为P,再过P作 ,垂足为Q,连接CQ,因为 平面 ,且 平面 ,
所以 ,
又因为 ,由于BD, 平面 ,且 ,
所以 平面 ,则 为直角三角形,
由于 平面 ,所以 ,
因为 , 平面CPQ,且 ,所以 平面CPQ,
因为 平面CPQ,所以 ,
则∠CQP为平面 与平面 的夹角或补角,
在 中,由等面积法可得 ,
因为 ,所以 ,
因此平面 与平面 夹角的余弦值为 .
17.(2024·河北保定·二模)如图,在四棱锥 中,平面 内存在一条直线 与 平行,
平面 ,直线 与平面 所成的角的正切值为 , , .(1)证明:四边形 是直角梯形.
(2)若点 满足 ,求二面角 的正弦值.
【答案】(1)证明见解析;
(2)
【分析】(1)根据条件,利用线面平行的判定定理,得到 平面 ,再线面平行的性质定理,得
到 ,再利用条件得到 ,结合 , ,即可证明结果;
(2)建立空间直角坐标系,求出平面 和平面 的法向量,利用面面角的向量法,即可解决问题.
【详解】(1)因为 , 平面 , 平面 ,所以 平面 ,
因为 平面 ,平面 平面 ,所以 ,
连接 ,因为 平面 ,所以 是 与平面 的夹角,
则 ,解得 .
因为 , ,所以 ,所以 .
又 ,所以四边形 是直角梯形.
(2)取 的中点M,连接 ,以A为坐标原点建立如图所示的空间直角坐标系,
则 , , , , , ,
,
由 ,得 ,则 ,设平面 的法向量为 ,
则 ,取 ,得到 ,即 ,
设平面 的一个法向量为 ,
则由 ,得到 ,到 ,得到 ,
所以平面 的一个法向量为
设二面角 的平面角为 ,
则 ,所以 ,
故二面角 的正弦值为 .
18.(2024·湖南衡阳·模拟预测)如图,在圆锥 中, 是圆锥的顶点, 是圆锥底面圆的圆心, 是
圆锥底面圆的直径,等边三角形 是圆锥底面圆 的内接三角形, 是圆锥母线 的中点,
.(1)求证:平面 平面 ;
(2)设点 在线段 上,且 ,求直线 与平面 所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】(1)借助圆锥的性质及面面垂直的判定定理计算即可得;
(2)建立适当空间直角坐标系,借助空间向量计算即可得.
【详解】(1)如图,设 交 于点 ,连接 ,
在圆锥 中, 底面圆 ,所以 ,
又等边三角形 是圆锥底面圆 的内接三角形, 为直径,所以 ,
所以 ,所以 ,
可知 ,即 是 的中点,
又 是母线 的中点,所以 ,所以 平面 ,
又 平面 ,所以平面 平面 ;
(2)由(1) 平面 ,以点 为坐标原点,所在直线分别为 轴、 轴、 轴,建立如图所示的空间直角坐标系,
在等腰三角形 中 ,
又 ,所以 ,
所以 ,
,
设平面 的法向量为 ,
则 ,即 ,
令 ,则 ,即 ,
设直线 与平面 所成的角为 ,
则 .
19.(2024·湖南岳阳·三模)已知四棱锥 的底面 是边长为4的菱形, ,
, , 是线段 上的点,且 .(1)证明: 平面 ;
(2)点 在直线 上,求 与平面 所成角的最大值.
【答案】(1)证明见解析;
(2) .
【分析】(1)连结 , 交于点 ,由条件证明 ,建立空间直角坐标系,利用向
量方法证明 ,结合线面垂直判定定理证明结论;
(2)根据线面角的向量求法求出 与平面 所成角的正弦值,再求其最大值,由此可求线面角的最
大值.
【详解】(1)连结 , 交于点 ,连 ,
由 ,
知 ,
又 平面
又底面 为菱形,所以
以 为坐标原点, , , 分别为x,y,z轴的正方向建立空间直角坐标系,
如图所示 ,边长为4,则 ,
在直角三角形 中, 所以
所以点
,则
所以 ,
所以 ,,
所以 ,
所以 ,
又 , 平面 ,
所以 平面 ,
(2)设 ,
所以 ,
故 ,
所以
平面 的一个法向量是 ,
设 与平面 所成角为 ,则
当 时, 平面 , ;
当 时,
,
当且仅当 时取等号,
又 所以 ,故 与平面 所成角的最大值为
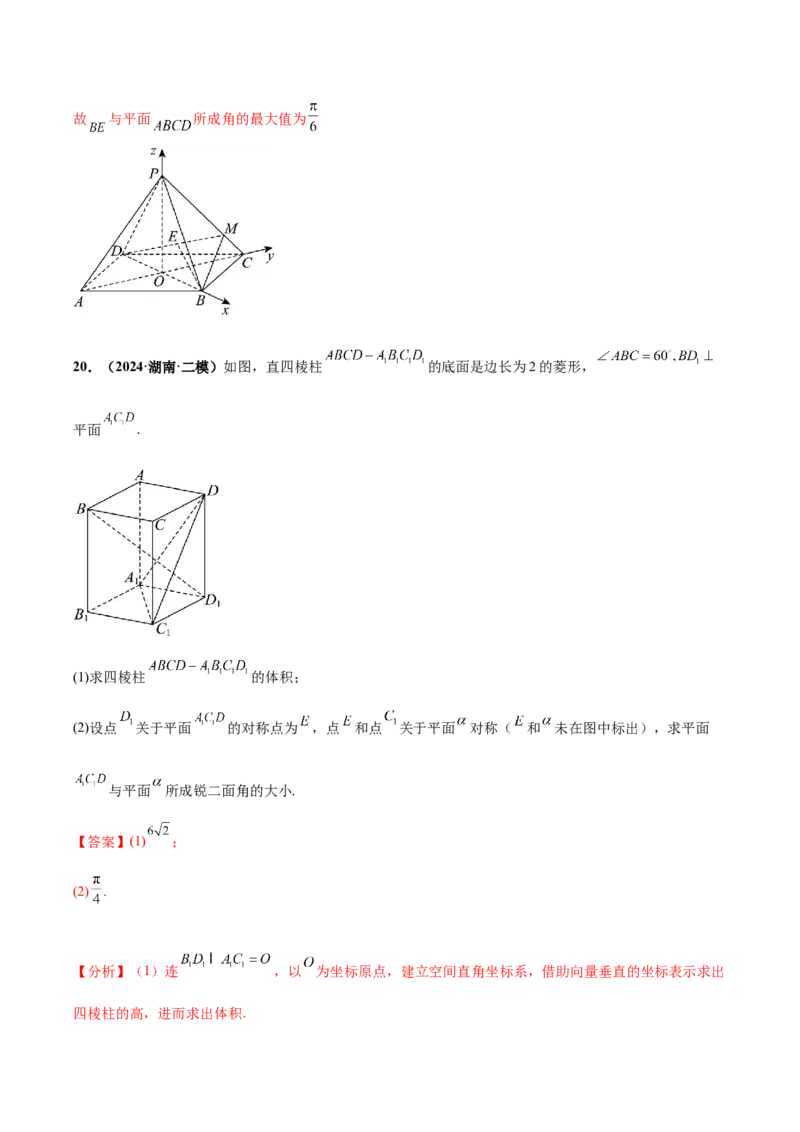
20.(2024·湖南·二模)如图,直四棱柱 的底面是边长为2的菱形,
平面 .
(1)求四棱柱 的体积;
(2)设点 关于平面 的对称点为 ,点 和点 关于平面 对称( 和 未在图中标出),求平面
与平面 所成锐二面角的大小.
【答案】(1) ;
(2) .
【分析】(1)连 ,以 为坐标原点,建立空间直角坐标系,借助向量垂直的坐标表示求出
四棱柱的高,进而求出体积.(2)利用对称求出点 的坐标,进而求出平面 与平面 的法向量,再借助面面角的向量求法求得结
果.
【详解】(1)在直四棱柱 中,连 ,由菱形 ,得 ,令
,
以 为坐标原点,直线 分别为 轴,过 平行于 的直线为 轴,建立空间直角坐标系,
则点 , ,
由 平面 , 平面 ,得 ,则 ,解得 ,
所以四棱柱的体积 .
(2)由(1)知, , ,
由 平面 ,点 关于平面 的对称点为 ,则点 在线段 上,且 ,
设 , ,则 ,
所以 ,
于是 ,解得 ,则 ,由点 和点 关于平面 对称,得 是平面 的一个法向量,
又 是平面 的一个法向量,
因此 ,
所以平面 和平面 所成锐二面角的大小为 .
21.(2024·山东济南·二模)如图,在四棱锥 中,四边形ABCD 为直角梯形,AB∥CD,
,平面 平面ABCD,F为线段BC的中点,E为线段
PF上一点.
(1)证明: ;
(2)当EF为何值时,直线BE 与平面PAD夹角的正弦值为 .
【答案】(1)证明见解析
(2)2
【分析】(1)过 作 ,垂足为 ,分析可知 为等边三角形,可得 ,结合面面
垂直的性质可得 平面ABCD,即可得结果;
(2)取线段 的中点 ,连接 ,建系,设 ,求平面PAD的法向量,利用空间向
量处理线面夹角的问题.
【详解】(1)过 作 ,垂足为 ,由题意知: 为矩形,可得 ,
由 ,则 为等边三角形,且F为线段BC的中点,则 ,
又因为平面 平面ABCD,平面 平面 , 平面 ,
可得 平面ABCD,且 平面 ,
所以 .
(2)由(1)可知: 平面ABCD,
取线段 的中点 ,连接 ,则 ∥ , ,
又因为 ,可知 ,
以 为坐标原点, 分别为 轴,建立空间直角坐标系,
则 ,
因为E为线段PF上一点,设 ,
可得 ,
设平面 的法向量 ,则 ,
令 ,则 ,可得 ,
由题意可得: ,
整理得 ,解得 ,
所以当 ,直线BE 与平面PAD夹角的正弦值为 .22.(2024·山东潍坊·二模)如图1,在平行四边形 中, , ,E为 的
中点,将 沿 折起,连结 , ,且 ,如图2.
(1)求证:图2中的平面 平面 ;
(2)在图2中,若点 在棱 上,直线 与平面 所成的角的正弦值为 ,求点 到平面 的
距离.
【答案】(1)证明见解析
(2)
【分析】(1)连接 ,利用勾股定理证明 ,再根据线面垂直的判定定理证得 平
面 ,再根据面面垂直的判定定理即可得证;
(2)以点 为原点,建立空间直角坐标系,利用向量法求解即可.
【详解】(1)连接 ,
由题意 ,
则 为等边三角形,
由余弦定理得 ,所以 ,
则 ,
所以 ,
又 平面 ,
所以 平面 ,
又 平面 ,所以平面 平面 ;(2)如图,以点 为原点,建立空间直角坐标系,
则 ,
设 ,
故 ,
,
因为 轴垂直平面 ,故可取平面 的一条法向量为 ,
所以 ,
化简得 ,解得 或 (舍去),
所以 ,
设平面 的法向量为 ,
则有 ,可取 ,
所以点 到平面 的距离为 .
23.(2024·福建·模拟预测)如图,在三棱锥 中, ,已知二面
角 的大小为 , .(1)求点P到平面 的距离;
(2)当三棱锥 的体积取得最大值时,求:
(Ⅰ)二面角 的余弦值;
(Ⅱ)直线 与平面 所成角.
【答案】(1)
(2)(Ⅰ)
(Ⅱ)
【分析】(1)可得 , ,过P作 的垂线交其于点D,过P作平面 的垂线交其
于点O,可得 平面 ,进而可得 为二面角 的平面角,可求得 ;
(2)(Ⅰ) ,令 , ,利用导数可求体积的最大
值,可求得 ;
(Ⅱ)由(Ⅰ)求得 , ,记点C到平面 的距离为h,利用等体积法求得h,可求
直线 与平面 所成的角.
【详解】(1)由已知,得 , ,
过P作 的垂线交其于点D,
过P作平面 的垂线交其于点O,
因为 平面 , 平面 ,所以 ,
因为 , 平面 , 平面 ,所以 平面 ,
因为 平面 ,所以 ,
所以 为二面角 的平面角, ,故 ;
(2)(Ⅰ) 三棱锥 的体积为 ,
令 ,则三棱锥 的体积 ,
所以 ,
当 , ,当 , ,
所以 在 上单调递增,在 上单调递减,
故当 时,三棱锥 的体积最大,此时 ;
所以二面角 的余弦值为 ;
(Ⅱ)求得此时体积为 ,可知此时 , ,
由平面几何知识知 , ,
记点C到平面 的距离为h,
由等体积法可知 ,求得 ,
记直线 与平面 所成角为 ,则 ,即 ,
所以直线 与平面 所成的角为 .24.(2024·浙江杭州·二模)如图,在多面体 中,底面 是平行四边形,
为 的中点, .
(1)证明: ;
(2)若多面体 的体积为 ,求平面 与平面 夹角的余弦值.
【答案】(1)证明见解析;
(2) .
【分析】(1)根据余弦定理求解 ,即可求证 ,进而根据线线垂直可证明线面垂直,
即可得线线垂直,
(2)根据体积公式,结合棱柱与棱锥的体积关系,结合等体积法可得 ,即可建立空间直角
坐标系,求解法向量求解.
【详解】(1)在 中,由余弦定理可得 ,
所以 ,所以 ,
所以 .
又因为 , 平面 ,
所以 平面 , 平面 .
所以 .
由于 ,所以四边形 为平行四边形,所以 .又 ,所以 ,
所以 .
(2)因为 ,所以 ,
又 , 平面 ,所以 平面 .
取 中点 ,连接 ,设 .
设多面体 的体积为 ,
则
.
解得 .
建立如图所示的空间直角坐标系,则 ,
.
则平面 的一个法向量 .
所以 ,
设平面 的一个法向量 ,
则 即 取 .所以 .
所以平面 与平面 夹角的余弦值为 .
25.(2024·浙江嘉兴·二模)在如图所示的几何体中,四边形 为平行四边形, 平面
, .
(1)证明:平面 平面 ;
(2)若 ,求平面 与平面 夹角的余弦值.
【答案】(1)证明见解析;
(2) .
【分析】(1)法一,先证明 ,再证明 平面 ,利用面面垂直的判定定理得证;法二,
建立空间直角坐标系,利用向量法求出平面 和平面 的法向量证明;
(2)法一,过 作 分别平行于 ,连结 ,作 交 于 点,连结 ,证明
,说明 为平面 与平面 的夹角,求解得答案;法二,建系求出平面 和平面
的法向量,利用向量法求解.
【详解】(1)解法一: ,在 中, ,即 ,
, ,
,又 ,
底面 , 底面 ,
, 平面 且相交于 ,
平面 ,又 平面 ,
平面 平面 .
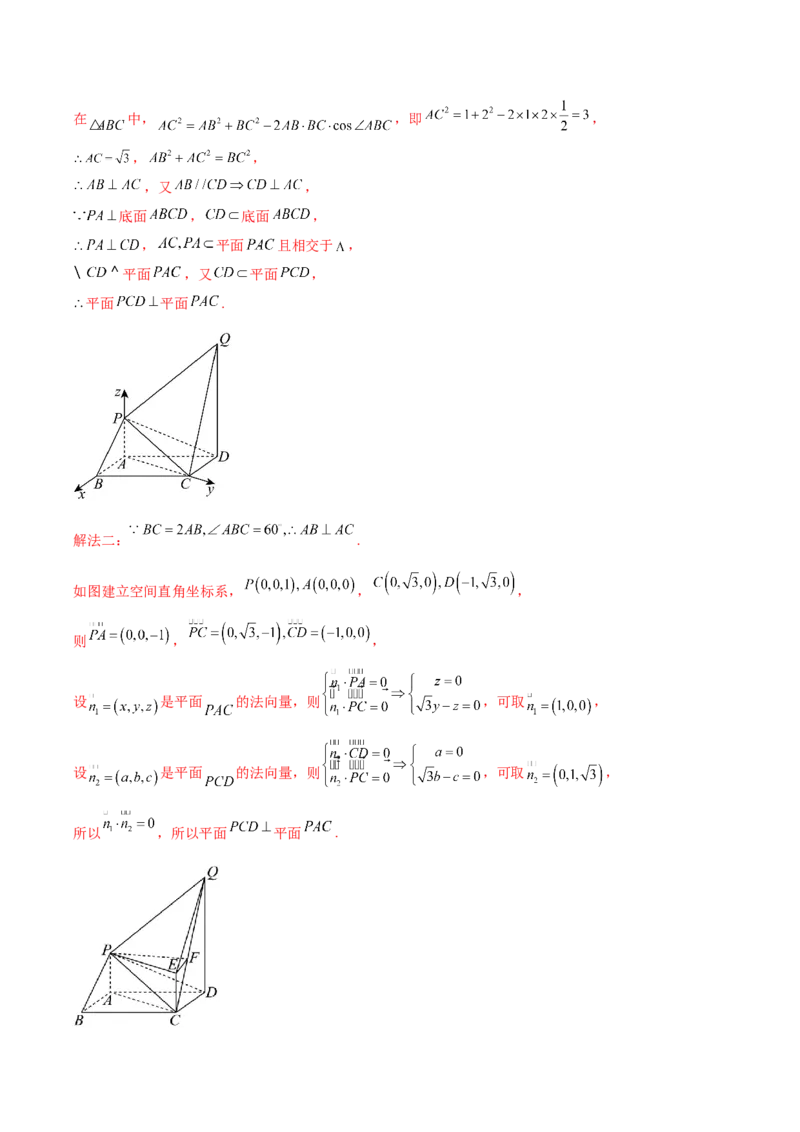
解法二: .
如图建立空间直角坐标系, , ,
则 , ,
设 是平面 的法向量,则 ,可取 ,
设 是平面 的法向量,则 ,可取 ,
所以 ,所以平面 平面 .(2)解法一:在直角梯形 中,因为 ,解得 ,
过 作 分别平行于 ,连结 ,作
交 于 点,连结 ,
, 且都在面 内,
平面 ,
平面 ,又 平面 ,
,又 , 平面 且交于 ,
平面 ,又 平面 ,
,
为平面 与平面 的夹角或其补角,
在 中, , ,
,由等面积法解得 ,又 ,
.
所以平面 与平面 夹角的余弦值为 .
(2)解法二:在直角梯形 中,解得 ,
如图建立空间直角坐标系, , ,
平面 的法向量为 ,又 ,
设平面 的法向量为 ,则 ,即 ,
令 ,解得 , ,设平面 与平面 夹角为 ,
所以 ,
即平面 与平面 夹角的余弦值为 .
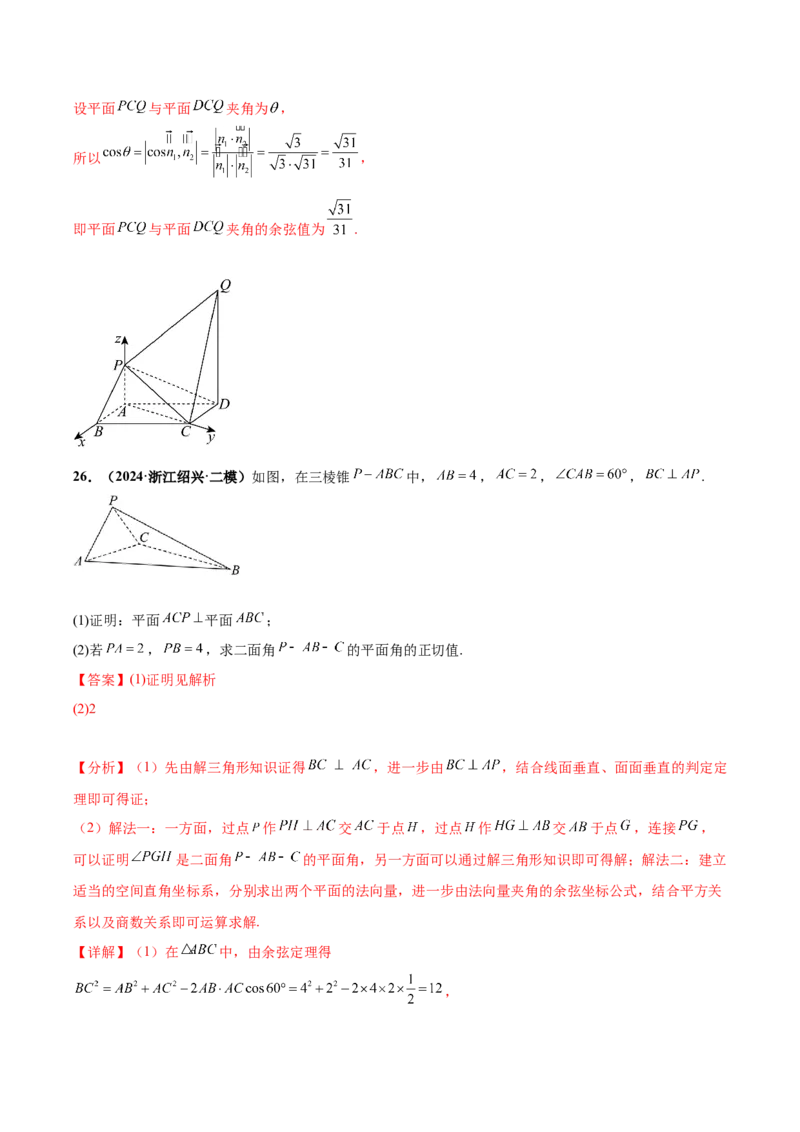
26.(2024·浙江绍兴·二模)如图,在三棱锥 中, , , , .
(1)证明:平面 平面 ;
(2)若 , ,求二面角 的平面角的正切值.
【答案】(1)证明见解析
(2)2
【分析】(1)先由解三角形知识证得 ,进一步由 ,结合线面垂直、面面垂直的判定定
理即可得证;
(2)解法一:一方面,过点 作 交 于点 ,过点 作 交 于点 ,连接 ,
可以证明 是二面角 的平面角,另一方面可以通过解三角形知识即可得解;解法二:建立
适当的空间直角坐标系,分别求出两个平面的法向量,进一步由法向量夹角的余弦坐标公式,结合平方关
系以及商数关系即可运算求解.
【详解】(1)在 中,由余弦定理得
,所以 ,所以 ,
又 , , 面 , 面 ,
所以 平面 ,
又 平面 ,所以平面 平面 .
(2)解法一:
过点 作 交 于点 ,
因为平面 平面 ,平面 平面 , 面 ,
所以 平面 ,因为 面 ,所以 ,
过点 作 交 于点 ,连接 ,
因为 , 面 , 面 ,
所以 面 ,因为 面 ,则 ,
所以 是二面角 的平面角.
由(1)知, 平面 ,因为 平面 ,所以 ,
所以 ,
又 ,所以三角形 是正三角形,
所以 , .
在直角三角形 中, ,
所以 .
所以,二面角 的平面角的正切值是2.
解法二:
以 为原点, , 所在直线为x,y轴,建立如图所示的空间直角坐标系 ,则 , ,设 ,其中 ,
由 , 得 ,
所以 , ,即 ,
所以 , .
设平面 的法向量为 ,
则 ,即 ,
取 ,则 , ,所以 .
又平面 的法向量为 ,
设二面角 的大小为 ,
因为 为锐角,所以 ,
所以 , ,
所以,二面角 的平面角的正切值为2.
27.(2024·河北沧州·一模)如图,在正三棱锥 中, ,点 满足 ,
,过点 作平面 分别与棱AB,BD,CD交于Q,S,T三点,且 , .(1)证明: ,四边形 总是矩形;
(2)若 ,求四棱锥 体积的最大值.
【答案】(1)证明见解析
(2)
【分析】(1)取 的中点 ,连接 ,根据条件可得 平面 ,从而得到 ,再
利用 平行于 ,可得出四边形 为平行四边形,即可证明;
(2)取 中点 ,连接 ,交平面 于点 ,根据条件得出 ,构造
函数 ,利用导数与函数的单调性间关系,求出 的最值,即可解决问题.
【详解】(1)当 时,点 是棱 上的动点(不包括端点),取 的中点 ,连接 ,
易知 ,又 , 平面 ,
所以 平面 ,又 面 ,所以 ,
又 平面 ,平面 平面 , 平面 ,所以 ,
同理 ,所以 ,
同理可得 ,所以四边形 为平行四边形,
又 或其补角是 与 所成的角,所以 ,故四边形 为矩形;
(2) ,由 ,得 ,又 ,得到 ,同理可得 ,
取 中点 ,连接 ,交平面 于点 .
因为 ,所以该正三棱锥为正四面体,所以 ,所以 ,
同理 , , ,
所以 , ,又 , 平面 ,
所以 平面 ,因为平面 与 都平行,
所以可得 ,又易知 ,所以 ,
即 到平面 的距离为 ,
所以 ,
令 ,则 ,
由 ,得到 ,由 ,得到 ,
所以 在 上单调递增,在 上单调递减,
所以 ,所以 .
28.(2024·湖北·二模)如图1.在菱形ABCD中, , , ,
,沿EF将 向上折起得到棱锥 .如图2所示,设二面角
的平面角为 .(1)当 为何值时,三棱锥 和四棱锥 的体积之比为 ?
(2)当 为何值时, ,平面PEF与平面PFB的夹角 的余弦值为 ?
【答案】(1)
(2)
【分析】(1)根据题意分析可知△AEF为正三角形, ,进而求正 、四边形BDEF
的面积,结合锥体的体积公式分析求解;
(2)建系,用 表示相关点的坐标,分别求平面PEF与平面PFB的法向量,根据面面夹角的向量求法
列式求解.
【详解】(1)因为 , ,所以 .
因为在菱形ABCD中, , ,
所以 为正三角形, ,
正 的面积为 ,四边形BDEF的面积为 ,
而三棱锥 和四棱锥 有相同的高(点P到平而BCDEF的距离),
所以其体积之比等于 ,解得 或 ,
因为 ,所以 .
(2)因为菱形ABCD的对角线互相垂直,
设AC与EF的交点为O,在翻折的过程中,始终有 , ,
所以二面角 的平面角为 ,在棱锥 中,显然有 ,
以O为坐标原点,OF,OC分别为x轴、y轴,
过O且与平面BCDEF垂直的直线为z轴,建立如图所示的空间直角坐标系.
因为 , ,
则 , , , ,
可得 , ,
设平面PEF的法向量为 ,则 ,
令 ,则 ,可得 ,
设平面PBF的法向量为 ,则 ,
令 ,则 ,可得 ,
由题意可得 ,解得 ,
且 ,所以当 时, .
29.(2024·湖北·模拟预测)空间中有一个平面 和两条直线m,n,其中m,n与 的交点分别为A,B,
,设直线m与n之间的夹角为 ,(1)如图1,若直线m,n交于点C,求点C到平面 距离的最大值;
(2)如图2,若直线m,n互为异面直线,直线m上一点P和直线n上一点Q满足 , 且
,
(i)求直线m,n与平面 的夹角之和;
(ii)设 ,求点P到平面 距离的最大值关于d的函数 .
【答案】(1) ;
(2)(i)证明见解析,(ii)
【分析】(1)设点C到平面 的距离为h,结合余弦定理、三角形,面积公式,基本不等式即可求得大值;
(2)利用空间直线之间的位置关系、线面垂直的性质定理与判定定理确定线面夹角即可证明结论;再根
据点到平面的距离,结合(1)中结论即可得答案.
【详解】(1)设点C到平面 的距离为h,作 于点H,可知 ,
设 , ,在 中,由余弦定理可知: ,
由于直线m与n之间的夹角为 ,且它们交于点C,则 或 ,
若 ,
则 ,又 ,则 ( 时取等);
因为 ,所以 ,所以点C到平面 的距离 ,其最大值为 ;
若 ,同理可得最大值为 .
综上,点C到平面 距离的最大值为 .
(2)(i)证:如图,过点P作直线 ,由题知直线l与平面 必相交于一点,设其为点D,
连接 , ,则P,Q,D,B共面,又 且 ,于是 ,
又 ,则四边形 为平行四边形,则 ,
因为 且 ,所以 且 ,所以 ,
又 平面 ,所以 平面 ,
作 于H,
因为 平面 ,则 ,又 ,则 ,
设 ,则P到平面 的距离也为h,且直线m,n与平面 的夹角分别为 和 ;
由于直线m与n之间的夹角为 ,则直线m与l之间的夹角也为 ,
则 或 ,
于是 ,或
即直线m,n与平面 的夹角之和为 或 ;
(ii)因为 平面 ,而 平面 ,所以 ,
中, ,则 ,
又 或 ,由(1)问同法算得 ,或 ,
即点P到平面 距离h的最大值为 .
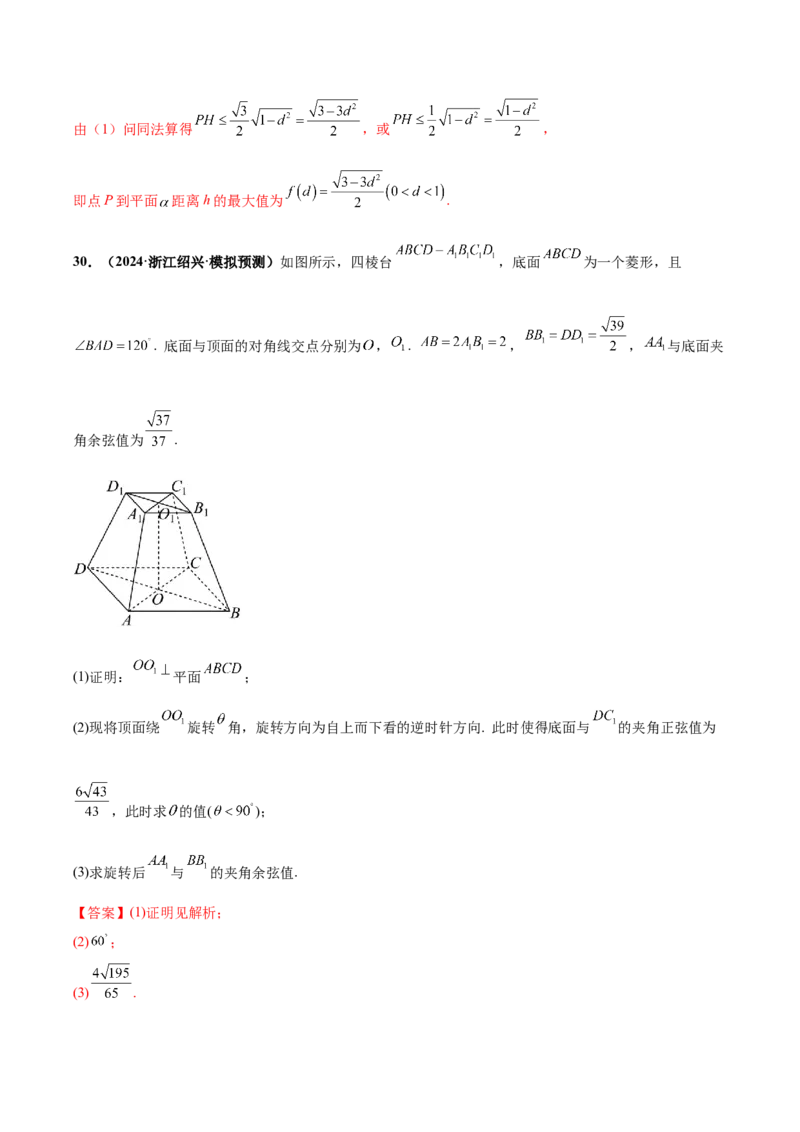
30.(2024·浙江绍兴·模拟预测)如图所示,四棱台 ,底面 为一个菱形,且
. 底面与顶面的对角线交点分别为 , . , , 与底面夹
角余弦值为 .
(1)证明: 平面 ;
(2)现将顶面绕 旋转 角,旋转方向为自上而下看的逆时针方向. 此时使得底面与 的夹角正弦值为
,此时求 的值( );
(3)求旋转后 与 的夹角余弦值.
【答案】(1)证明见解析;
(2) ;
(3) .【分析】(1)先在等腰梯形 证明 ,求出 ;再证明 即 与底面夹角,利
用 ,及余弦定理解得 ,再利用勾股定理有 ,所以可证
平面 .
(2)根据题意建立合适的空间直角坐标系,易得平面 的一个法向量 ,根据旋转方向和旋
转前的位置,写出 坐标为 ;再根据底面与 的夹角正弦值为 ,求出 .
(3)与第二问的原理相同,根据旋转方向和旋转前的位置写出 ,
,即 , ,从而得到旋转后 与 的夹
角余弦值 .
【详解】(1)连接 , ,过点 作 于点 ,取 中点 ,连接 ,如图.
由题易得 , . 所以 .在四棱台 中易得 ,
又因为 且 ,所以四边形 为等腰梯形.
因为 , 分别是 和 的中点,所以 ,
又因为 ,易得等腰梯形 的高 .
因为在菱形 中 ,且 面 , ,
所以 面 ,又因为 面 ,
所以 ,又因为 ,且 面 , ,
所以 面 ,因此 即 与底面夹角.
由题易得 ,且 ,所以四边形 为平行四边形,所以 .
则 ,
在 中由余弦定理可得 ,解得 .
所以 ,由勾股定理得 .
又因为 ,且 面 , ,
所以 平面 .
(2)因为 ,
所以 为原点, , , 方向分别为 , , 轴正方向建立如图所示空间直角坐标系.
易得平面 的一个法向量 ,旋转前坐标分别为: , , , , , .
点 旋转的过程俯视如图:
因为在旋转过程中 不变,且点 所在终边对应的角大小为 ,逆时针旋转 角后点 坐标为
,即 ,所以
所以底面与 的夹角正弦值为 ,
解得 ,又因为 ,所以 .
(3)由第二问可得,因为点 所在终边对应的角为 ,所以旋转后点 ,即
;同理因为点 所在终边对应的角为 ,所以旋转后点 ,即
.
所以 , ,
因此旋转后 与 的夹角余弦值为 .