文档内容
第一章 单元质量测评
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间
120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四
个选项中,只有一项是符合题目要求的)
1.下列语句是命题的是( )
A.2x2+3x-1>0 B.比较两数大小
C.撸起袖子加油干! D.cos45°=
答案 D
解析 A项不能判断真假,不是命题;B,C两项不是陈述句,不是命题;D
项是命题.
2.下面所给三个命题中真命题的个数是( )
①若ac2>bc2,则a>b;
②若四边形的对角互补,则该四边形是圆的内接四边形;
③若二次函数y=ax2+bx+c中,b2-4ac<0,则该二次函数的图象与x轴有
公共点.
A.0 B.1
C.2 D.3
答案 C
解析 ①该命题为真命题,由ac2>bc2,得c2>0,则有a>b.②该命题为真命题,
根据圆内接四边形的定义可进行判定.③该命题为假命题,因为当b2-4ac<0时,
一元二次方程ax2+bx+c=0没有实数根,因此二次函数的图象与 x轴无公共点.
综上所述,故选C.
3.命题“∀x∈R,|x|+x2≥0”的否定是( )
A.∀x∈R,|x|+x2<0
B.∀x∈R,|x|+x2≤0
C.∃x∈R,|x|+x2<0
D.∃x∈R,|x|+x2≥0
答案 C
解析 “∀x∈R,|x|+x2≥0”的否定是“∃x∈R,|x|+x2<0”.
4.已知x ,x ∈R,则“x >1且x >1”是“x +x >2且x x >1”的( )
1 2 1 2 1 2 1 2
A.充分不必要条件B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 A
解析 由x >1且x >1得x +x >1+1=2,x x >1×1=1,所以“x >1且
1 2 1 2 1 2 1
x >1”是“x +x >2且x x >1”的充分条件;设x =3,x =,则x +x =>2
2 1 2 1 2 1 2 1 2
且x x =>1,但x <1,所以不满足必要性.故选A.
1 2 2
5.下列命题中,真命题有( )
①mx2+2x-1=0是关于x的一元二次方程;②抛物线y=ax2+2x-1与x轴
至少有一个交点;③互相包含的两个集合相等;④空集是任何集合的真子集.
A.1个 B.2个
C.3个 D.4个
答案 A
解析 对于①来说,当m=0时,mx2+2x-1=0是一元一次方程;对于②来
说,抛物线y=ax2+2x-1对应的一元二次方程的判别式 Δ=4+4a,当a<-1时,
方程无实数根,此时抛物线与x轴无交点;③正确,A⊆B,B⊆A⇔A=B;空集是
任何集合的子集,是任何非空集合的真子集,故④错误.
6.“a2+(b-1)2=0”是“a(b-1)=0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 A
解析 a2+(b-1)2=0⇒a=0且b=1,而a(b-1)=0⇒a=0或b=1,故“a2
+(b-1)2=0”是“a(b-1)=0”的充分不必要条件.
7.已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B中所
含元素的个数为( )
A.3 B.6
C.8 D.10
答案 D
解析 当x=5时,y=1,2,3,4;当x=4时,y=1,2,3;当x=3时,y=1,2;
当x=2时,y=1,共10个.故选D.
8.在下列命题中,真命题的个数是( )
①∀x∈R,x2+x+3>0;
②∀x∈Q,x2+1是有理数;
③关于x的方程x2+|x|-6=0有四个实数根;④∃x,y∈Z,3x-2y=10.
A.1 B.2
C.3 D.4
答案 C
解析 ①中,x2+x+3=2+>0,故①是真命题;②中,∵x∈Q,∴x2+1是有
理数,故②是真命题;③中,由x2+|x|-6=0,得|x|=2,∴x=±2,方程有两个
实数根,故③是假命题;④中,当x=4,y=1时,结论成立,故④是真命题.
由以上可知,正确选项为C.
9.给出下列四个命题:
①设集合X={x|x>-1},则{0}∈X;
②空集是任何集合的真子集;
③集合A={y|y=},B={x|y=}表示同一集合;
④集合P={a,b},集合Q={b,a},则P=Q.
其中正确的命题是( )
A.①② B.①③
C.③④ D.④
答案 D
解析 ①中{0}与X均表示集合,不能用∈来表示集合与集合之间的关系,
①不正确;②中空集是任何非空集合的真子集,②不正确;③中A={y|y≥0},B
={x|x≥1或x≤-1},故不是同一集合,③不正确;④中根据集合中元素的无序
性知④正确.故选D.
10.下列命题中,是全称量词命题且是真命题的是( )
A.对任意的a,b∈R,都有a2+b2-2a-2b+2<0
B.菱形的两条对角线相等
C.∀x∈R,=x
D.正方形是矩形
答案 D
解析 A中的命题是全称量词命题,但 a2+b2-2a-2b+2=(a-1)2+(b-
1)2≥0,故是假命题;B中的命题是全称量词命题,但是假命题;C中的命题是
全称量词命题,但=|x|,故是假命题;D中的命题是全称量词命题且是真命题,
故选D.
11.设U为全集,A,B是集合,则“存在集合 C使得A⊆C,B⊆∁U C”是
“A∩B=∅”的( )
A.充分而不必要的条件
B.必要而不充分的条件C.充要条件
D.既不充分也不必要的条件
答案 C
解析
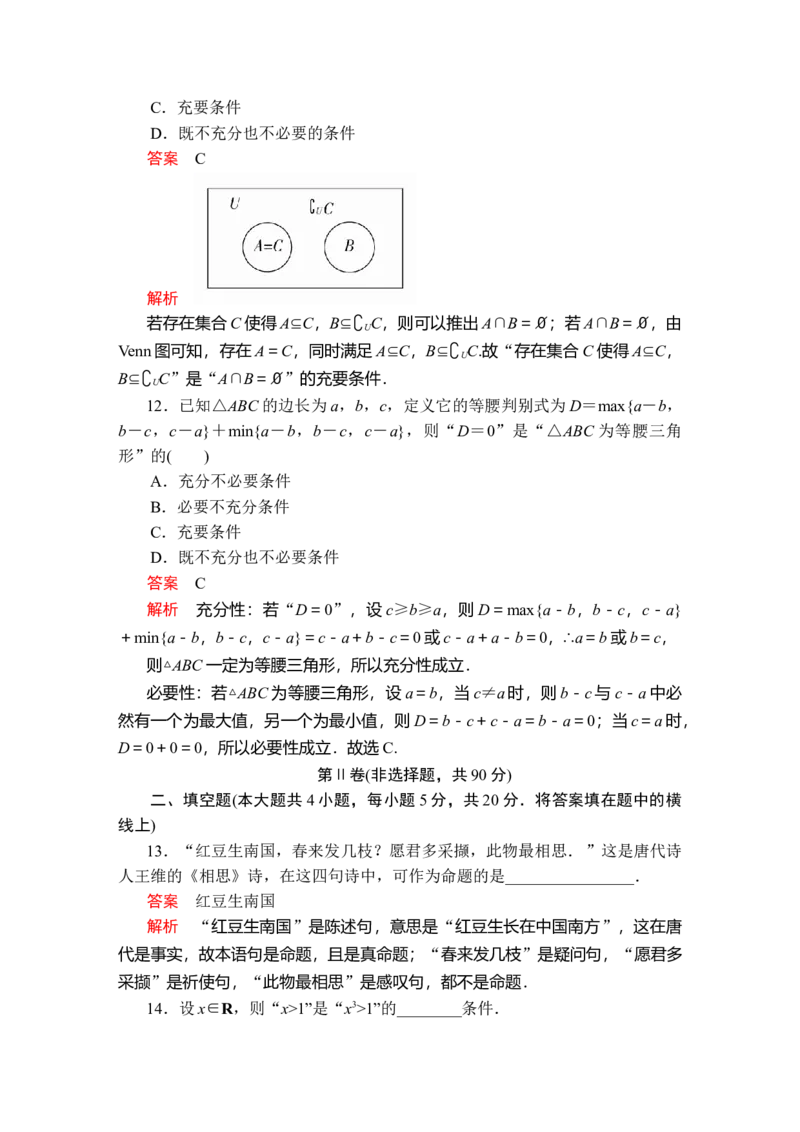
若存在集合C使得A⊆C,B⊆∁U C,则可以推出A∩B=∅;若A∩B=∅,由
Venn图可知,存在A=C,同时满足A⊆C,B⊆∁U C.故“存在集合C使得A⊆C,
B⊆∁U C”是“A∩B=∅”的充要条件.
12.已知△ABC的边长为a,b,c,定义它的等腰判别式为D=max{a-b,
b-c,c-a}+min{a-b,b-c,c-a},则“D=0”是“△ABC 为等腰三角
形”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 C
解析 充分性:若“D=0”,设c≥b≥a,则D=max{a-b,b-c,c-a}
+min{a-b,b-c,c-a}=c-a+b-c=0或c-a+a-b=0,∴a=b或b=c,
则△ABC一定为等腰三角形,所以充分性成立.
必要性:若△ABC为等腰三角形,设a=b,当c≠a时,则b-c与c-a中必
然有一个为最大值,另一个为最小值,则D=b-c+c-a=b-a=0;当c=a时,
D=0+0=0,所以必要性成立.故选C.
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横
线上)
13.“红豆生南国,春来发几枝?愿君多采撷,此物最相思.”这是唐代诗
人王维的《相思》诗,在这四句诗中,可作为命题的是________________.
答案 红豆生南国
解析 “红豆生南国”是陈述句,意思是“红豆生长在中国南方”,这在唐
代是事实,故本语句是命题,且是真命题;“春来发几枝”是疑问句,“愿君多
采撷”是祈使句,“此物最相思”是感叹句,都不是命题.
14.设x∈R,则“x>1”是“x3>1”的________条件.答案 充要
解析 因为x∈R,“x>1”⇔“x3>1”,所以“x>1”是“x3>1”的充要条件.
15.命题p:∀x∈R,x2+x+1≠0,则命题綈p为________________.
答案 ∃x∈R,x2+x+1=0
解析 命题p是全称量词命题,根据全称量词命题的否定是改量词,否结论,
则是∃x∈R,x2+x+1=0.
16.由命题“∃x∈R,x2+2x+m=0”是假命题,求得实数m的取值范围是
m>a,则实数a=________.
答案 1
解析 因为命题“∃x∈R,x2+2x+m=0”是假命题,所以其否定
“∀x∈R,x2+2x+m≠0”是真命题,等价于方程x2+2x+m=0无实根,所以Δ
=4-4m<0,解得m>1,又因为m的取值范围是(a,+∞),所以实数a=1.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或
演算步骤)
17.(本小题满分10分)写出下列命题的否定,并判断真假.
(1)p :∃x∈R,x2-x+1≤0;
1
(2)p :所有的菱形都是平行四边形;
2
(3)p :有的梯形是等腰梯形;
3
(4)p :任意x∈Z,x2的个位数字不等于3;
4
(5)p :有一个素数含三个正因数.
5
解 (1)綈p :∀x∈R,x2-x+1>0;真命题.
1
(2)綈p :存在一个菱形,它不是平行四边形;假命题.
2
(3)綈p :所有的梯形都不是等腰梯形;假命题.
3
(4)綈p :存在x∈Z,使x2的个位数字等于3;假命题.
4
(5)綈p :所有的素数都不含三个正因数;真命题.
5
18.(本小题满分12分)已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-
1},且B≠∅.
(1)若“命题p:∀x∈B,x∈A”是真命题,求m的取值范围;
(2)若“命题q:∃x∈A,x∈B”是真命题,求m的取值范围.
解 (1)∵A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},且 B≠∅,“命题
p:∀x∈B,x∈A”是真命题,
∴B⊆A,B≠∅,∴
解得2≤m≤3.
(2)q为真,则A∩B≠∅.
∵B≠∅,∴m≥2,∴∴2≤m≤4.
19.(本小题满分12分)已知集合A={x|-1