文档内容
黄金冲刺大题03 立体几何
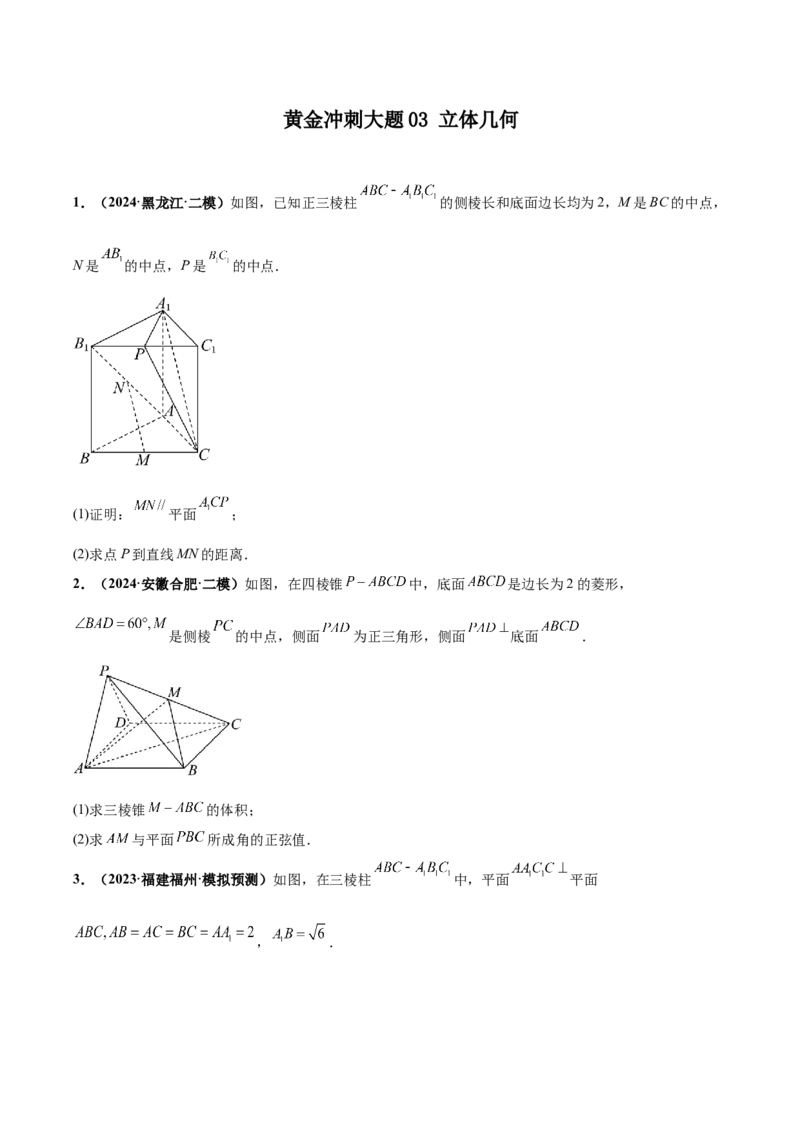
1.(2024·黑龙江·二模)如图,已知正三棱柱 的侧棱长和底面边长均为2,M是BC的中点,
N是 的中点,P是 的中点.
(1)证明: 平面 ;
(2)求点P到直线MN的距离.
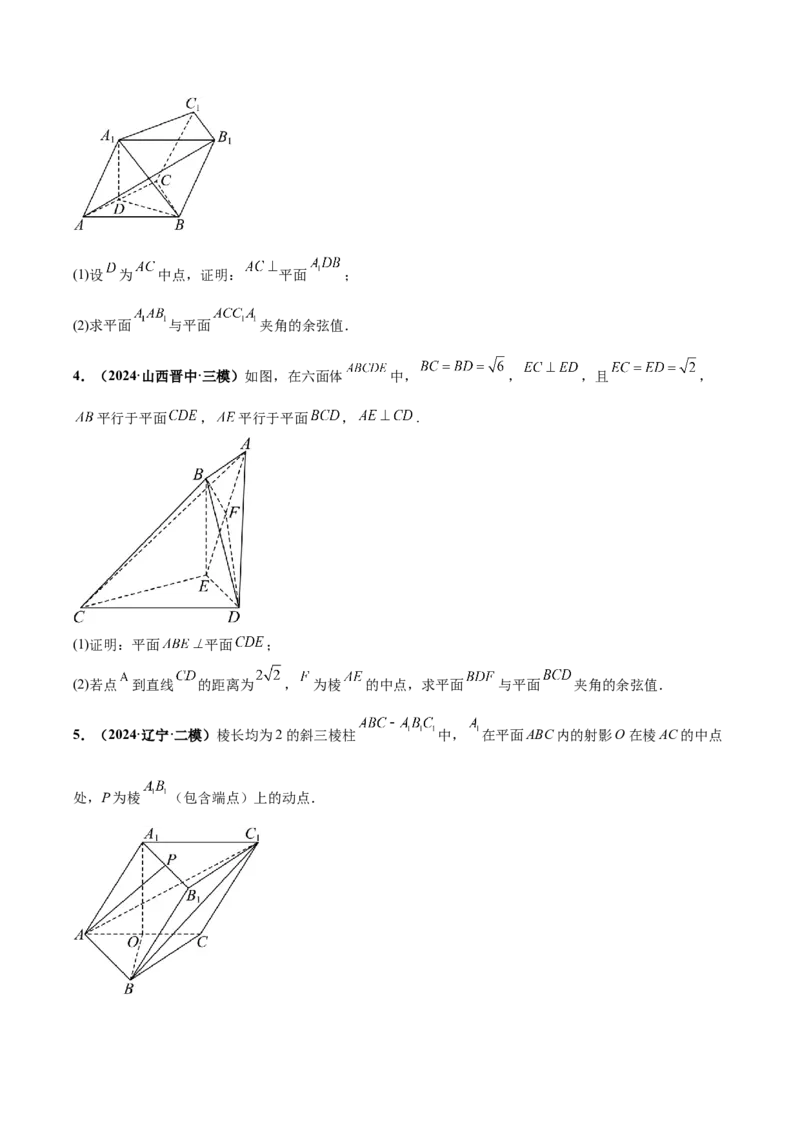
2.(2024·安徽合肥·二模)如图,在四棱锥 中,底面 是边长为2的菱形,
是侧棱 的中点,侧面 为正三角形,侧面 底面 .
(1)求三棱锥 的体积;
(2)求 与平面 所成角的正弦值.
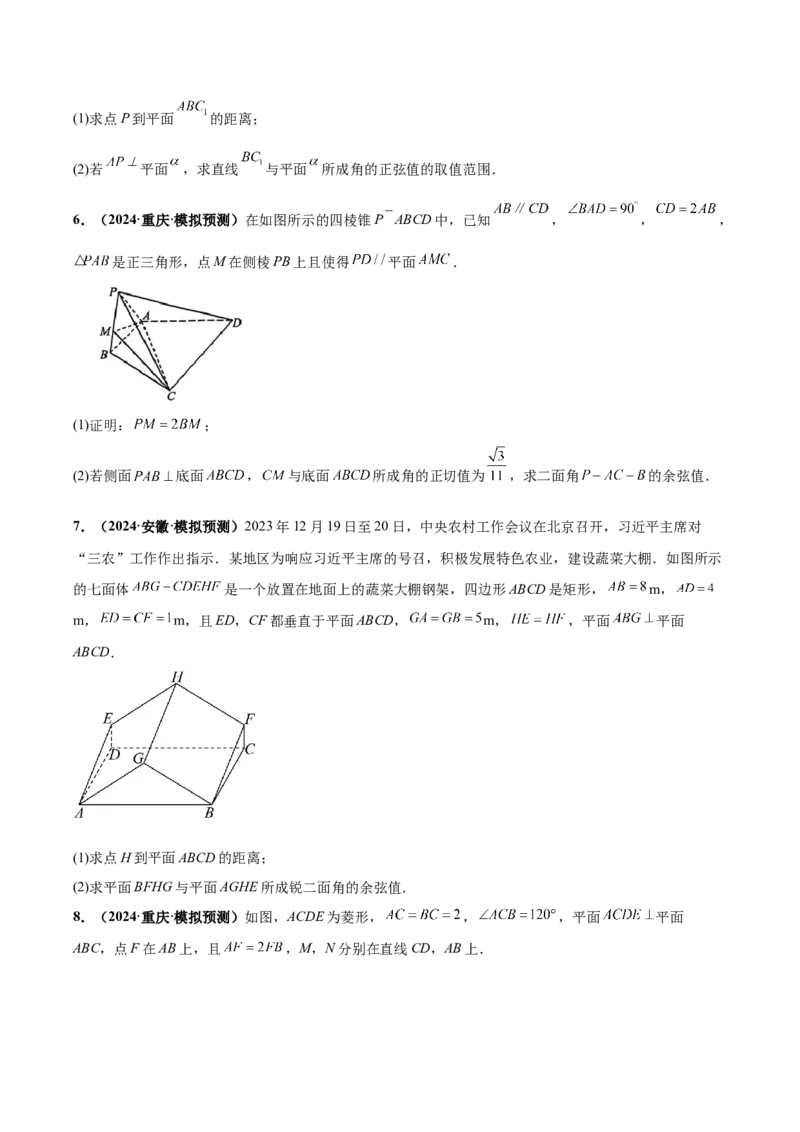
3.(2023·福建福州·模拟预测)如图,在三棱柱 中,平面 平面
, .(1)设 为 中点,证明: 平面 ;
(2)求平面 与平面 夹角的余弦值.
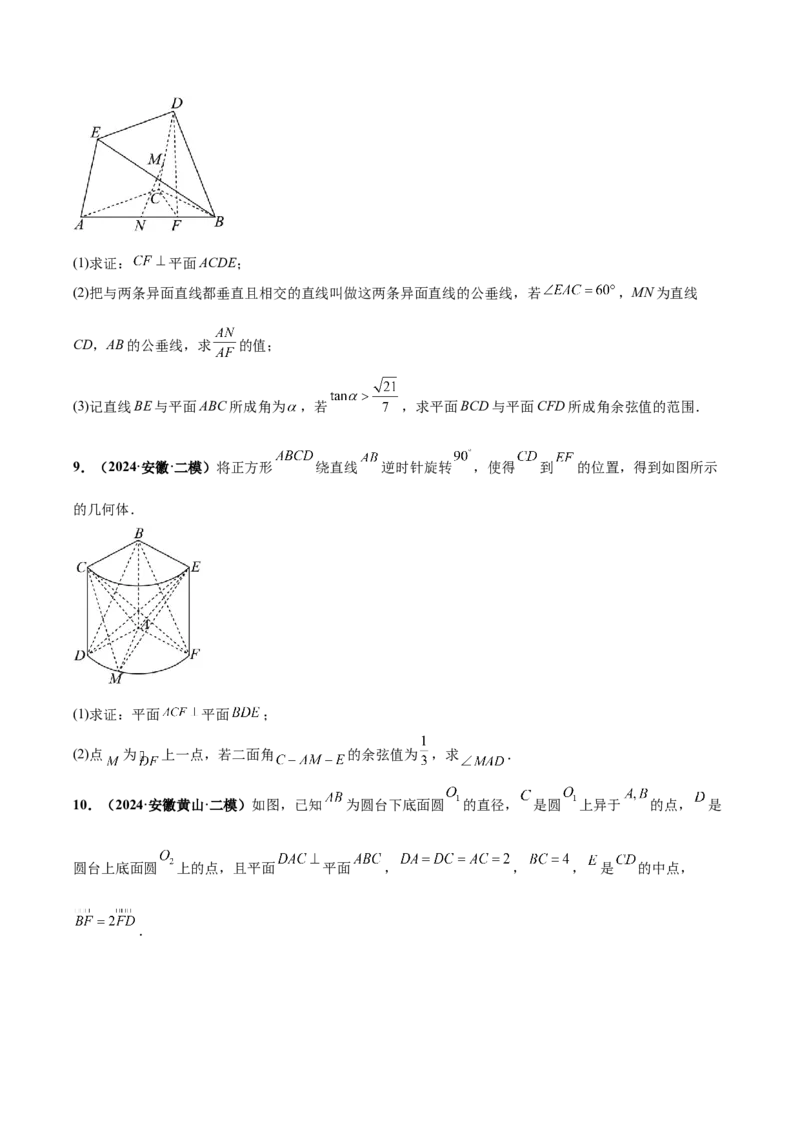
4.(2024·山西晋中·三模)如图,在六面体 中, , ,且 ,
平行于平面 , 平行于平面 , .
(1)证明:平面 平面 ;
(2)若点 到直线 的距离为 , 为棱 的中点,求平面 与平面 夹角的余弦值.
5.(2024·辽宁·二模)棱长均为2的斜三棱柱 中, 在平面ABC内的射影O在棱AC的中点
处,P为棱 (包含端点)上的动点.(1)求点P到平面 的距离;
(2)若 平面 ,求直线 与平面 所成角的正弦值的取值范围.
6.(2024·重庆·模拟预测)在如图所示的四棱锥P ABCD中,已知 , , ,
是正三角形,点M在侧棱PB上且使得 平面 .
(1)证明: ;
(2)若侧面 底面 , 与底面 所成角的正切值为 ,求二面角 的余弦值.
7.(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对
“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示
的七面体 是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形, m,
m, m,且ED,CF都垂直于平面ABCD, m, ,平面 平面
ABCD.
(1)求点H到平面ABCD的距离;
(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.
8.(2024·重庆·模拟预测)如图,ACDE为菱形, , ,平面 平面
ABC,点F在AB上,且 ,M,N分别在直线CD,AB上.(1)求证: 平面ACDE;
(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若 ,MN为直线
CD,AB的公垂线,求 的值;
(3)记直线BE与平面ABC所成角为 ,若 ,求平面BCD与平面CFD所成角余弦值的范围.
9.(2024·安徽·二模)将正方形 绕直线 逆时针旋转 ,使得 到 的位置,得到如图所示
的几何体.
(1)求证:平面 平面 ;
(2)点 为 上一点,若二面角 的余弦值为 ,求 .
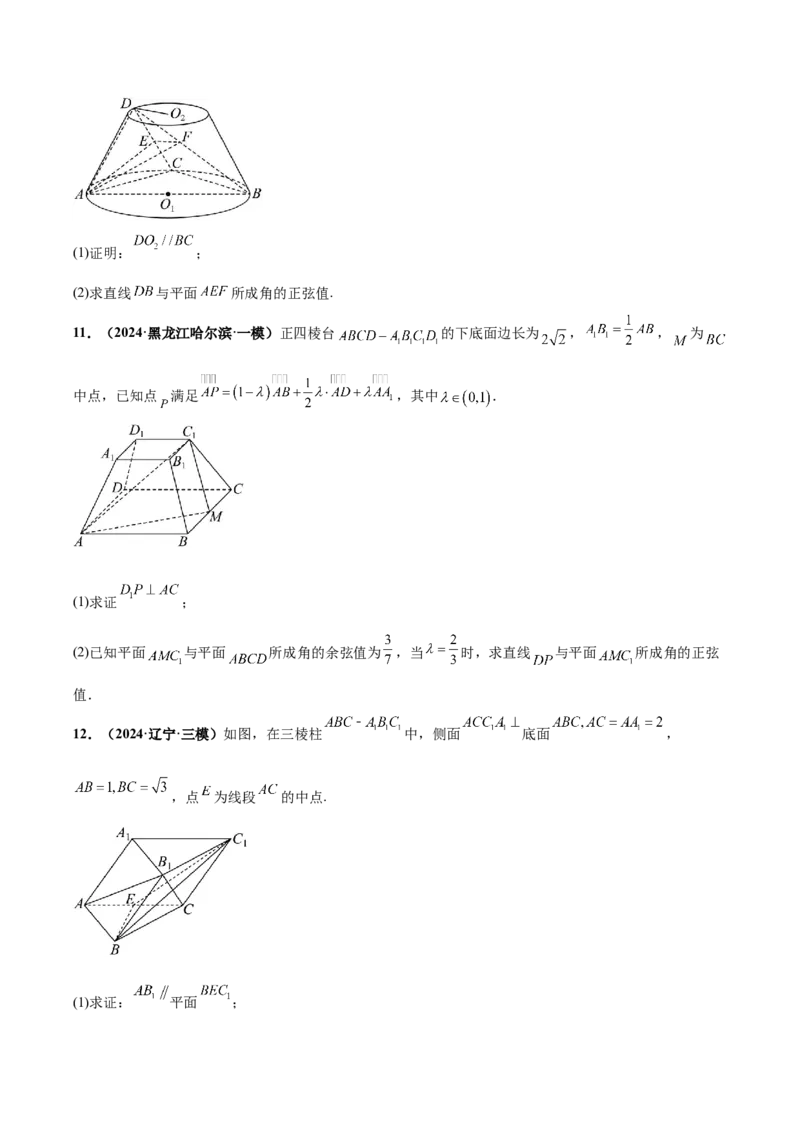
10.(2024·安徽黄山·二模)如图,已知 为圆台下底面圆 的直径, 是圆 上异于 的点, 是
圆台上底面圆 上的点,且平面 平面 , , , 是 的中点,
.(1)证明: ;
(2)求直线 与平面 所成角的正弦值.
11.(2024·黑龙江哈尔滨·一模)正四棱台 的下底面边长为 , , 为
中点,已知点 满足 ,其中 .
(1)求证 ;
(2)已知平面 与平面 所成角的余弦值为 ,当 时,求直线 与平面 所成角的正弦
值.
12.(2024·辽宁·三模)如图,在三棱柱 中,侧面 底面 ,
,点 为线段 的中点.
(1)求证: 平面 ;(2)若 ,求二面角 的余弦值.
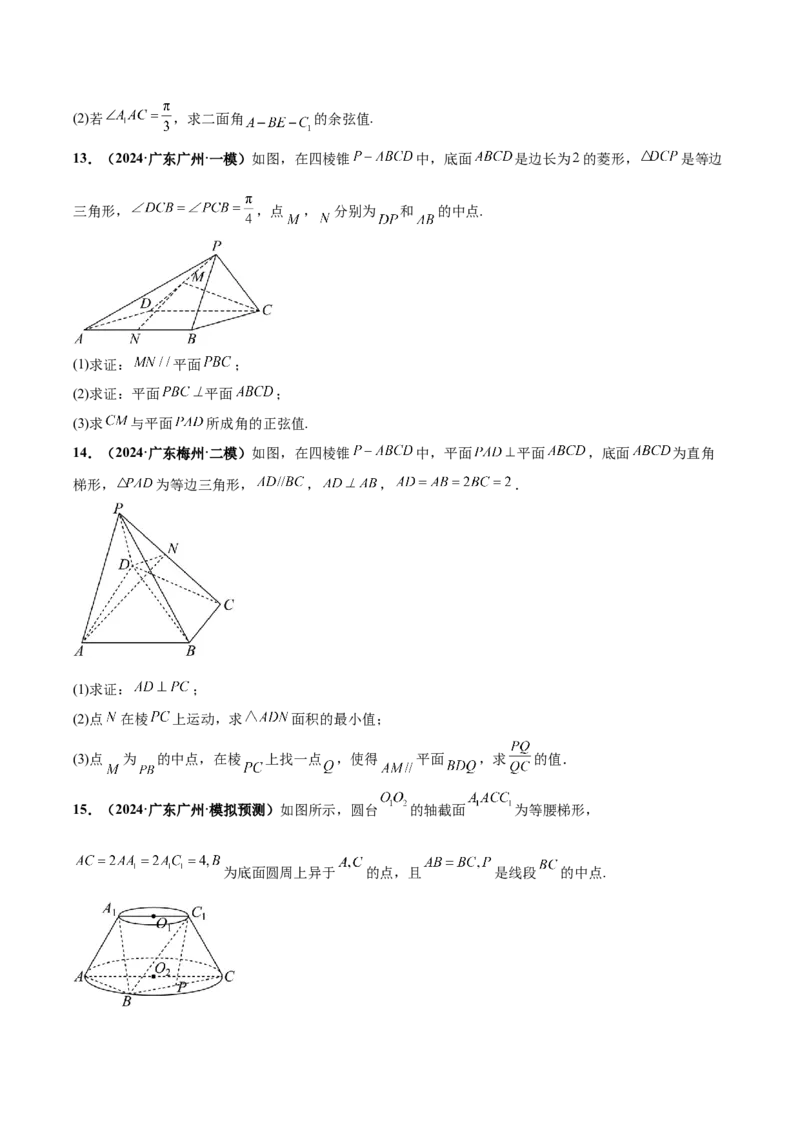
13.(2024·广东广州·一模)如图,在四棱锥 中,底面 是边长为 的菱形, 是等边
三角形, ,点 , 分别为 和 的中点.
(1)求证: 平面 ;
(2)求证:平面 平面 ;
(3)求 与平面 所成角的正弦值.
14.(2024·广东梅州·二模)如图,在四棱锥 中,平面 平面 ,底面 为直角
梯形, 为等边三角形, , , .
(1)求证: ;
(2)点 在棱 上运动,求 面积的最小值;
(3)点 为 的中点,在棱 上找一点 ,使得 平面 ,求 的值.
15.(2024·广东广州·模拟预测)如图所示,圆台 的轴截面 为等腰梯形,
为底面圆周上异于 的点,且 是线段 的中点.(1)求证: 平面 .
(2)求平面 与平面 夹角的余弦值.
16.(2024·广东深圳·二模)如图,三棱柱 中,侧面 底面ABC,且 ,
.
(1)证明: 平面ABC;
(2)若 , ,求平面 与平面 夹角的余弦值.
17.(2024·河北保定·二模)如图,在四棱锥 中,平面 内存在一条直线 与 平行,
平面 ,直线 与平面 所成的角的正切值为 , , .
(1)证明:四边形 是直角梯形.
(2)若点 满足 ,求二面角 的正弦值.
18.(2024·湖南衡阳·模拟预测)如图,在圆锥 中, 是圆锥的顶点, 是圆锥底面圆的圆心, 是
圆锥底面圆的直径,等边三角形 是圆锥底面圆 的内接三角形, 是圆锥母线 的中点,.
(1)求证:平面 平面 ;
(2)设点 在线段 上,且 ,求直线 与平面 所成角的正弦值.
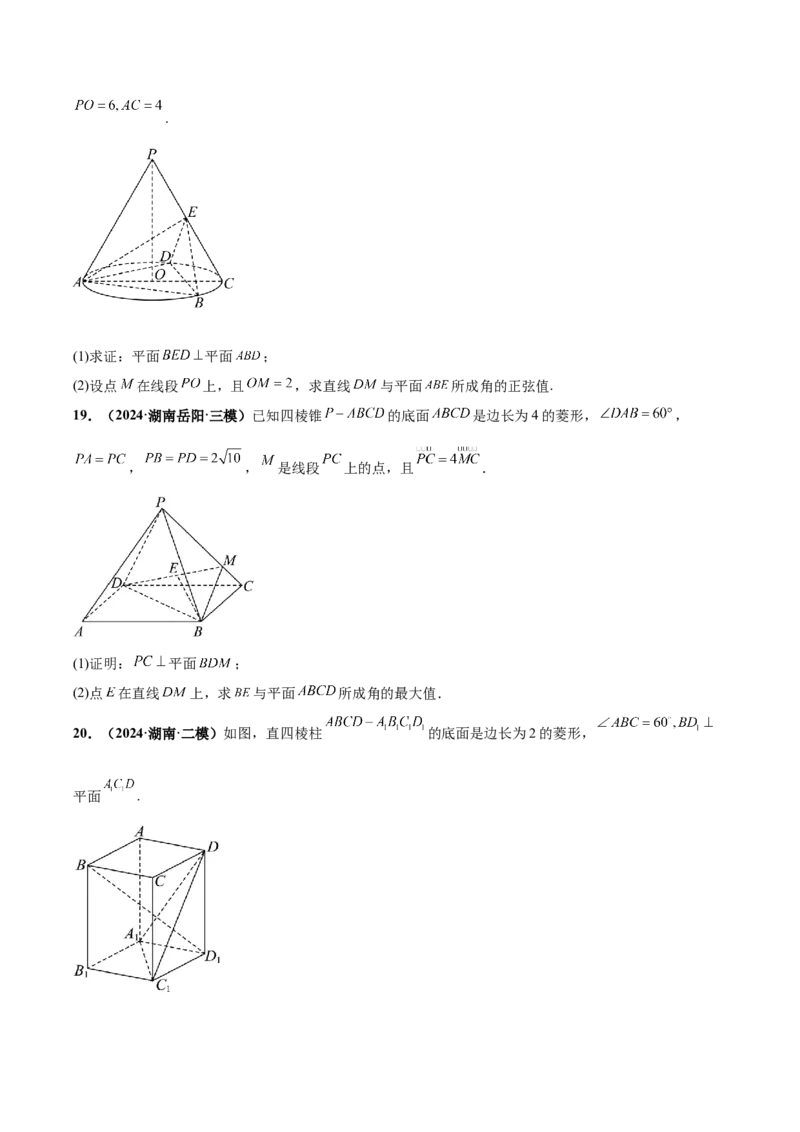
19.(2024·湖南岳阳·三模)已知四棱锥 的底面 是边长为4的菱形, ,
, , 是线段 上的点,且 .
(1)证明: 平面 ;
(2)点 在直线 上,求 与平面 所成角的最大值.
20.(2024·湖南·二模)如图,直四棱柱 的底面是边长为2的菱形,
平面 .(1)求四棱柱 的体积;
(2)设点 关于平面 的对称点为 ,点 和点 关于平面 对称( 和 未在图中标出),求平面
与平面 所成锐二面角的大小.
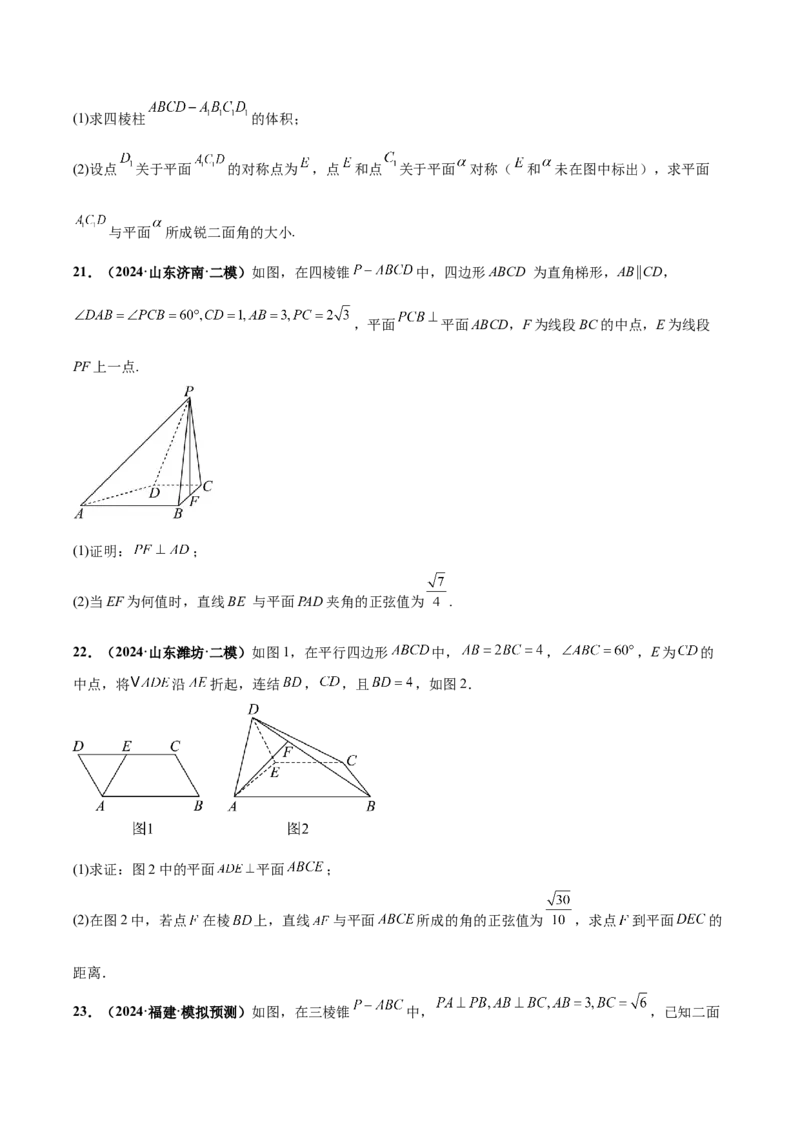
21.(2024·山东济南·二模)如图,在四棱锥 中,四边形ABCD 为直角梯形,AB∥CD,
,平面 平面ABCD,F为线段BC的中点,E为线段
PF上一点.
(1)证明: ;
(2)当EF为何值时,直线BE 与平面PAD夹角的正弦值为 .
22.(2024·山东潍坊·二模)如图1,在平行四边形 中, , ,E为 的
中点,将 沿 折起,连结 , ,且 ,如图2.
(1)求证:图2中的平面 平面 ;
(2)在图2中,若点 在棱 上,直线 与平面 所成的角的正弦值为 ,求点 到平面 的
距离.
23.(2024·福建·模拟预测)如图,在三棱锥 中, ,已知二面角 的大小为 , .
(1)求点P到平面 的距离;
(2)当三棱锥 的体积取得最大值时,求:
(Ⅰ)二面角 的余弦值;
(Ⅱ)直线 与平面 所成角.
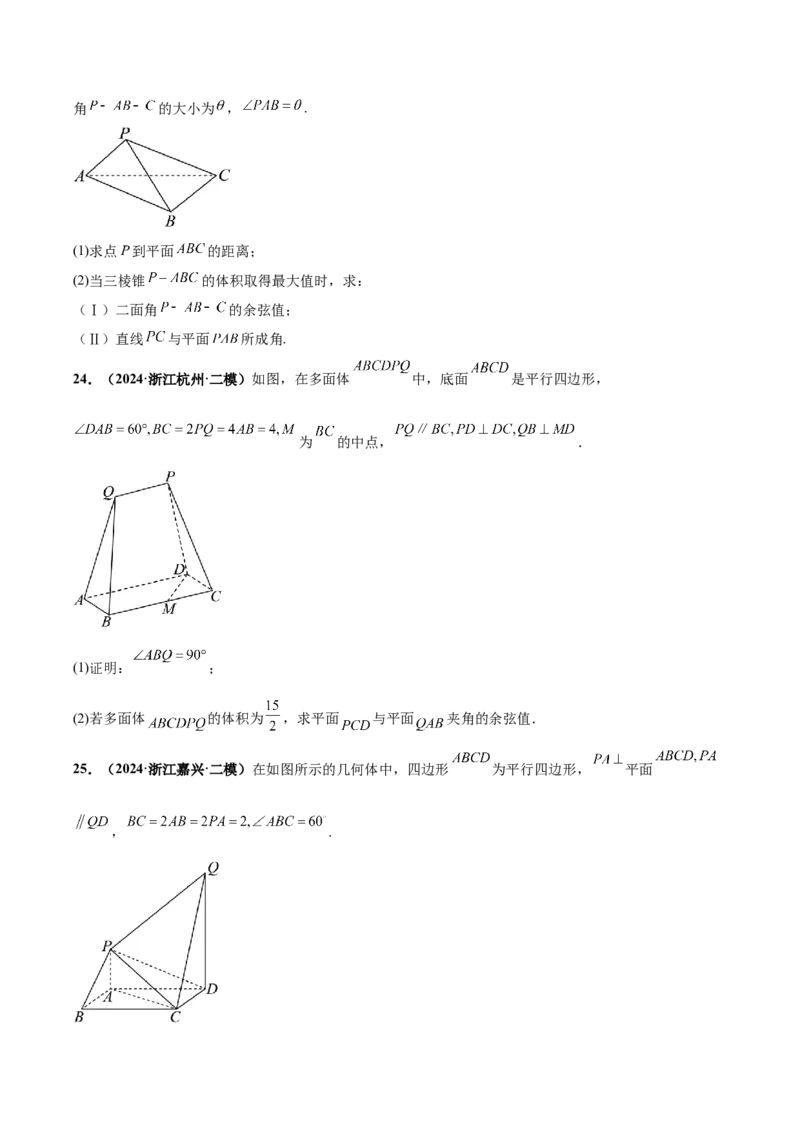
24.(2024·浙江杭州·二模)如图,在多面体 中,底面 是平行四边形,
为 的中点, .
(1)证明: ;
(2)若多面体 的体积为 ,求平面 与平面 夹角的余弦值.
25.(2024·浙江嘉兴·二模)在如图所示的几何体中,四边形 为平行四边形, 平面
, .(1)证明:平面 平面 ;
(2)若 ,求平面 与平面 夹角的余弦值.
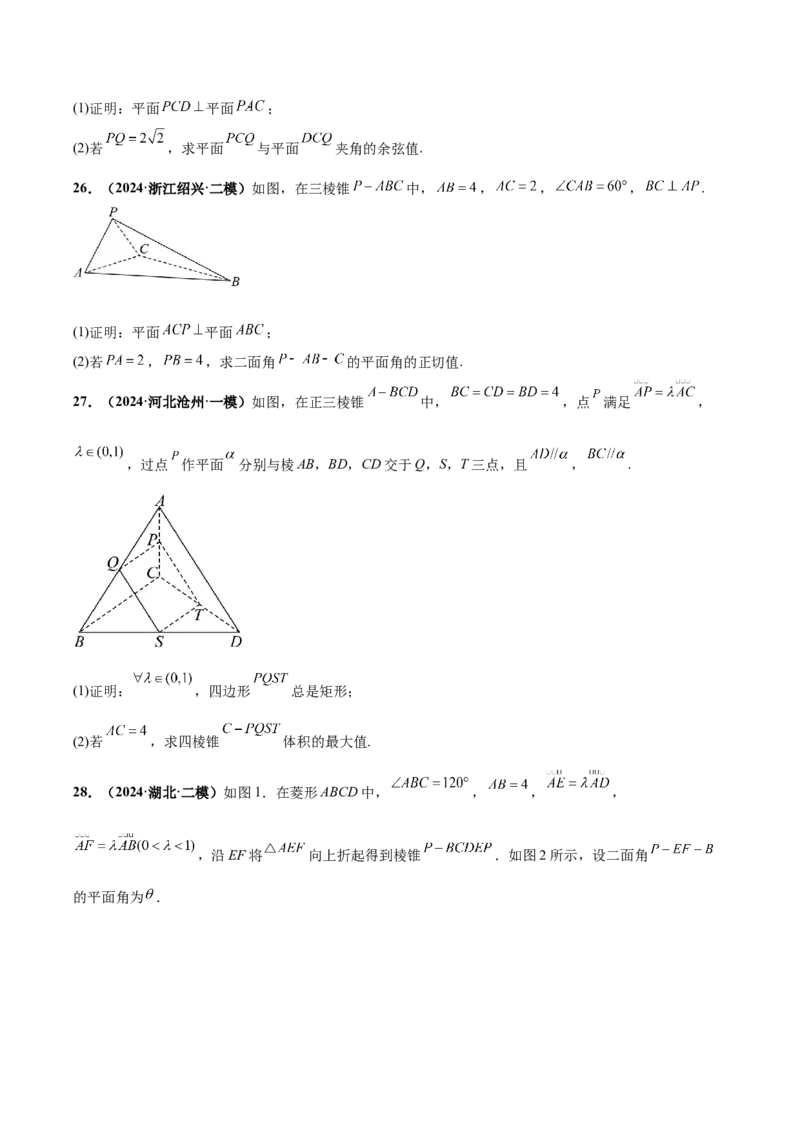
26.(2024·浙江绍兴·二模)如图,在三棱锥 中, , , , .
(1)证明:平面 平面 ;
(2)若 , ,求二面角 的平面角的正切值.
27.(2024·河北沧州·一模)如图,在正三棱锥 中, ,点 满足 ,
,过点 作平面 分别与棱AB,BD,CD交于Q,S,T三点,且 , .
(1)证明: ,四边形 总是矩形;
(2)若 ,求四棱锥 体积的最大值.
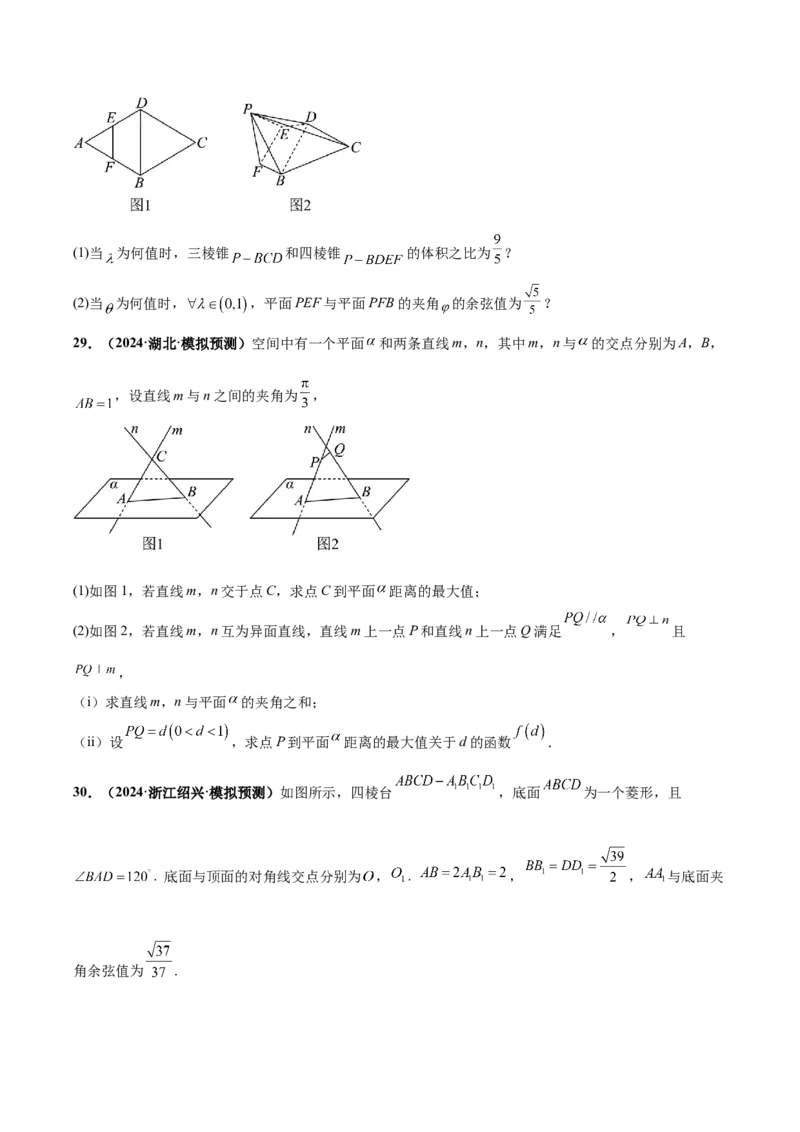
28.(2024·湖北·二模)如图1.在菱形ABCD中, , , ,
,沿EF将 向上折起得到棱锥 .如图2所示,设二面角
的平面角为 .(1)当 为何值时,三棱锥 和四棱锥 的体积之比为 ?
(2)当 为何值时, ,平面PEF与平面PFB的夹角 的余弦值为 ?
29.(2024·湖北·模拟预测)空间中有一个平面 和两条直线m,n,其中m,n与 的交点分别为A,B,
,设直线m与n之间的夹角为 ,
(1)如图1,若直线m,n交于点C,求点C到平面 距离的最大值;
(2)如图2,若直线m,n互为异面直线,直线m上一点P和直线n上一点Q满足 , 且
,
(i)求直线m,n与平面 的夹角之和;
(ii)设 ,求点P到平面 距离的最大值关于d的函数 .
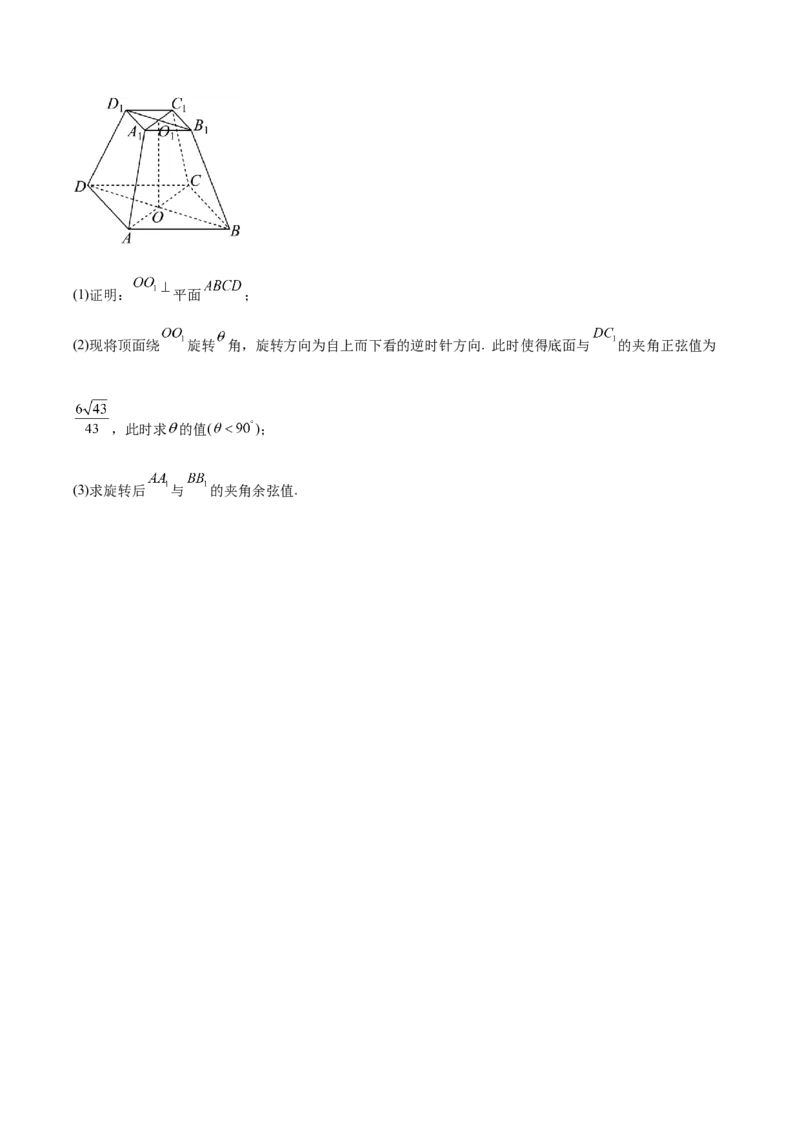
30.(2024·浙江绍兴·模拟预测)如图所示,四棱台 ,底面 为一个菱形,且
. 底面与顶面的对角线交点分别为 , . , , 与底面夹
角余弦值为 .(1)证明: 平面 ;
(2)现将顶面绕 旋转 角,旋转方向为自上而下看的逆时针方向. 此时使得底面与 的夹角正弦值为
,此时求 的值( );
(3)求旋转后 与 的夹角余弦值.