第一章1．2课后课时精练_E015高中全科试卷_数学试题_必修1_02.同步练习_5.同步练习（第五套）_（新教材）人教数学必修第1（课件+课时练+单元测试+复习）第1章(共36份打包)

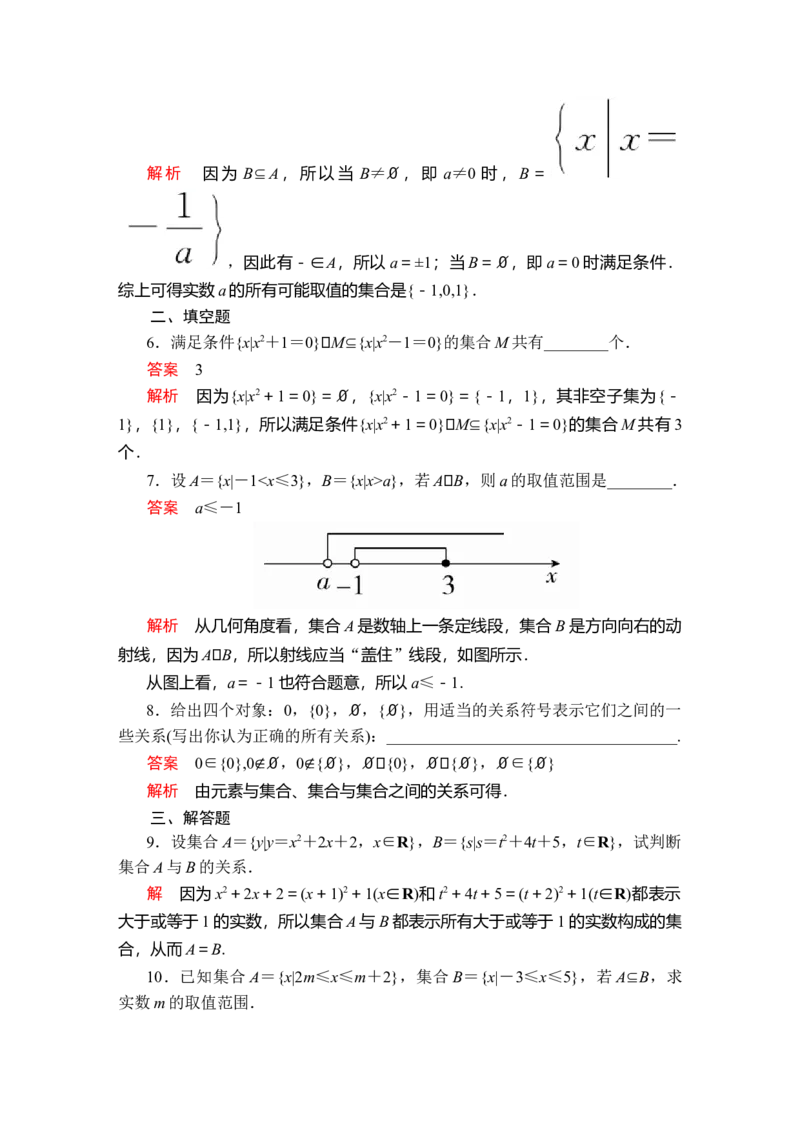
A级：“四基”巩固训练 一、选择题 1．下列关系式不正确的是( ) A．{1}⊆{1,2} B．{0}⊆{1,2} C．{2}⊆{1,2} D．1∈{1,2} 答案 B 解析 ∵0∉{1,2}，∴{0}⊆{1,2}不正确；根据子集的概念可知 A，C正确；D 显然正确． 2．若集合M＝，N＝，P＝，则M，N，P的关系是( ) A．M＝NP B．MN＝P C．MNP D．NPM 答案 B 解析 M＝，N＝＝(n∈Z，q＝n－1∈Z)，P＝x＝}，p∈Z.∴MN＝P. 3．若集合A满足A⊆B，A⊆C，B＝{0,1,2,3}，C＝{0,2,4,8}，则满足上述条 件的集合A的个数为( ) A．0 B．1 C．2 D．4 答案 D 解析 ∵A⊆B，A⊆C，∴A中最多能含有0,2两个元素，∴A＝∅，{0}，{2}， {0,2}共4个． 4．已知集合A＝{(x，y)|y＝x}和B＝ ， 则下列结论正确的是  A.1∈A B.B⊆A C.1，1⊆B D.∅∈A 答案 B 解析 B＝ ＝{1，1}，故B⊆A. 5.已知集合A＝{－1，1}，B＝{x|ax＋1＝0}，若B⊆A，则实数a的所有可能 取值的集合为  A.{－1} B.{1} C.{－1，1} D.{－1，0，1} 答案 D解析 因为 B⊆A，所以当 B≠∅，即 a≠0 时，B＝ ，因此有－∈A，所以a＝±1；当B＝∅，即a＝0时满足条件． 综上可得实数a的所有可能取值的集合是{－1,0,1}． 二、填空题 6．满足条件{x|x2＋1＝0}M⊆{x|x2－1＝0}的集合M共有________个． 答案 3 解析 因为{x|x2＋1＝0}＝∅，{x|x2－1＝0}＝{－1，1}，其非空子集为{－ 1}，{1}，{－1,1}，所以满足条件{x|x2＋1＝0}M⊆{x|x2－1＝0}的集合M共有3 个． 7．设A＝{x|－1a}，若AB，则a的取值范围是________． 答案 a≤－1 解析 从几何角度看，集合A是数轴上一条定线段，集合 B是方向向右的动 射线，因为AB，所以射线应当“盖住”线段，如图所示． 从图上看，a＝－1也符合题意，所以a≤－1. 8．给出四个对象：0，{0}，∅，{∅}，用适当的关系符号表示它们之间的一 些关系(写出你认为正确的所有关系)：____________________________________. 答案 0∈{0},0∉∅，0∉{∅}，∅{0}，∅{∅}，∅∈{∅} 解析 由元素与集合、集合与集合之间的关系可得． 三、解答题 9．设集合A＝{y|y＝x2＋2x＋2，x∈R}，B＝{s|s＝t2＋4t＋5，t∈R}，试判断 集合A与B的关系． 解 因为x2＋2x＋2＝(x＋1)2＋1(x∈R)和t2＋4t＋5＝(t＋2)2＋1(t∈R)都表示 大于或等于1的实数，所以集合A与B都表示所有大于或等于1的实数构成的集 合，从而A＝B. 10．已知集合A＝{x|2m≤x≤m＋2}，集合B＝{x|－3≤x≤5}，若A⊆B，求 实数m的取值范围．解 ①当A＝∅时，满足题意， 此时，2m>m＋2，即m>2； ②当A≠∅时，由A⊆B，得 解得－≤m≤2. 综上可得，实数m的取值范围是m≥－. B级：“四能”提升训练 1．已知集合A＝{0,1}，B＝{x|x⊆A}，试用列举法表示集合B，并判断A与B 的关系． 解 对于集合B，从“x⊆A”可知，B中的元素是集合A的子集． 所以B＝{∅，{0}，{1}，{0,1}} 很明显，集合A是集合B的一个元素，从而A∈B. 2．设集合A＝{x|x2＋4x＝0}，集合B＝{x|x2＋2(a＋1)x＋a2－1＝0，x∈R}， 若B⊆A，求实数a的取值范围． 解 易知A＝{－4,0}，因为B⊆A，所以分B＝A和BA两种情况． ①当A＝B时，B＝{－4,0}，则有－4,0是方程x2＋2(a＋1)x＋a2－1＝0的两 根，于是得a＝1. ②当BA时，若B＝∅，则Δ＝4(a＋1)2－4(a2－1)<0，解得a<－1； 若B≠∅，则B＝{－4}或{0}，Δ＝4(a＋1)2－4(a2－1)＝0， 解得a＝－1，验证知B＝{0}满足条件， 综上可知，所求实数a的值满足a＝1或a≤－1.