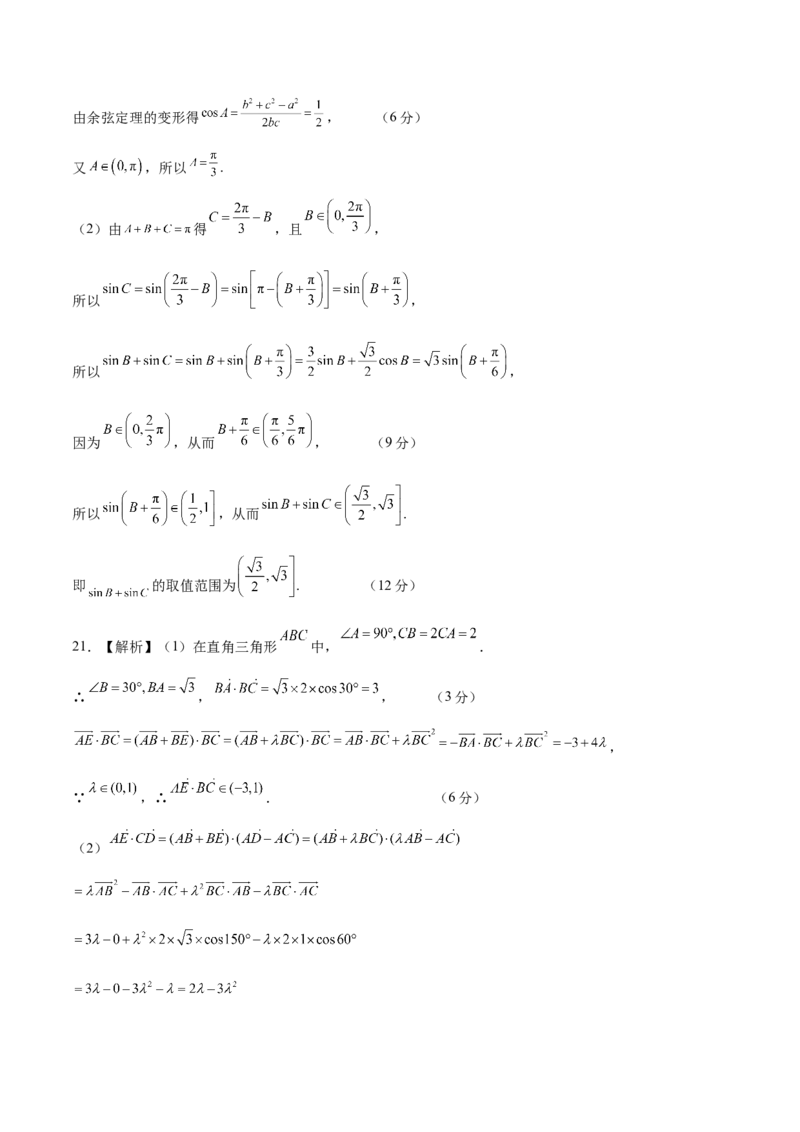文档内容
第一次月考 B 卷
高一数学·参考答案
1 2 3 4 5 6 7 8 9 10 11 12
A A A A A B B C AD ABC AD BD
13.1(5分)
14.1(5分)
15. (5分)
16. (5分)
17.【解析】(1)∵ 为实数,
∴ ,又∵ 为非零实数,∴ . (5分)
(2)∵ ,∴ ,
∴ 为纯虚数,
∴ ∴m的值为2. (10分)
18.【解析】(1) ,
因为 为实数,所以 , ,
结合θ范围,解得 ,所以 . (6分)
(2)复数 ,
复数 、 对应的向量分别是 , , ,
, (8分)又 ,
,
所以
,得 ,
因为 ,所以 ,所以 .
所以 ,解得 或 .
所以实数 的取值范围是 . (12分)
19.【解析】(1)
(3分)
因为 与 共线,
所以 解得 .
故当 时, 与 共线. (6分)
(2)因为A,B,C三点共线, 与 不共线,
所以存在实数λ,使得
即 ,
整理得
所以 ,解得 .故 的值为 . (12分)
20.【解析】(1)由正弦定理可得 ,即 ,由余弦定理的变形得 , (6分)
又 ,所以 .
(2)由 得 ,且 ,
所以 ,
所以 ,
因为 ,从而 , (9分)
所以 ,从而 .
即 的取值范围为 . (12分)
21.【解析】(1)在直角三角形 中, .
∴ , , (3分)
,
∵ ,∴ . (6分)
(2)令 ,得 或 (舍).
∴存在实数 ,使得 . (12分)
22.【解析】(1)由正弦定理,得 ,即 ,
故 , (3分)
因为 ,所以 ,
所以 ; (6分)
(2)由(1)知 ,
因为 的面积为 ,所以 ,解得 , (8分)
在 中,由正弦定理,得 ,
在 中,由正弦定理,得 ,
因为AD为角A的角平分线,所以 ,
又 ,所以 ,所以 ,
不妨设 , ,则 ,故 ,
延长 至点E,使得 ,连接 ,
则 ,又 ,
所以 ,故 , , (10分)
则 , ,
则 , ,在 中,由余弦定理,得 ,
即 ,
因为 ,所以 ,
其中 ,当且仅当 ,即 时,等号成立,
故 ,故 .
所以 长的最大值为 . (12分)