文档内容
黄金冲刺大题01 解三角形(精选30题)
1.(2024·江苏·一模)记 的内角 的对边分别为 ,已知 .
(1)证明: ;
(2)若 ,求 的周长.
【答案】(1)证明见解析
(2)
【分析】(1)利用正弦定理边化角结合角范围可证;
(2)利用倍角公式求得 ,然后利用正弦定理可得
【详解】(1)
因为
或 (舍), .
(2)由 ,结合(1)知 ,则 ,得
,
,
,由正弦定理得
的周长为 .
2.(2024·湖南常德·三模)在 中,内角 , , 的对边分别为 , , ,且
.
(1)求角 ;
(2)若 , , 成等差数列,且 的面积为 ,求 的周长.
【答案】(1)
(2)15
【分析】(1)先利用正弦定理角化边得出 ;再结合余弦定理得出 即可求解.
(2先根据 , , 成等差数列得出 ;再利用三角形的面积公式得出 ;最后结合(1)中的
,求出 , , 即可解答.
【详解】(1)因为 ,
由正弦定理 可得: .
由余弦定理可得: .
又因为 ,
所以 .
(2)由 , , 成等差数列可得: ①.
因为三角形 的面积为 , ,
,即 ②.由(1)知: ③
由①②③解得: .
,
故三角形 的周长为15.
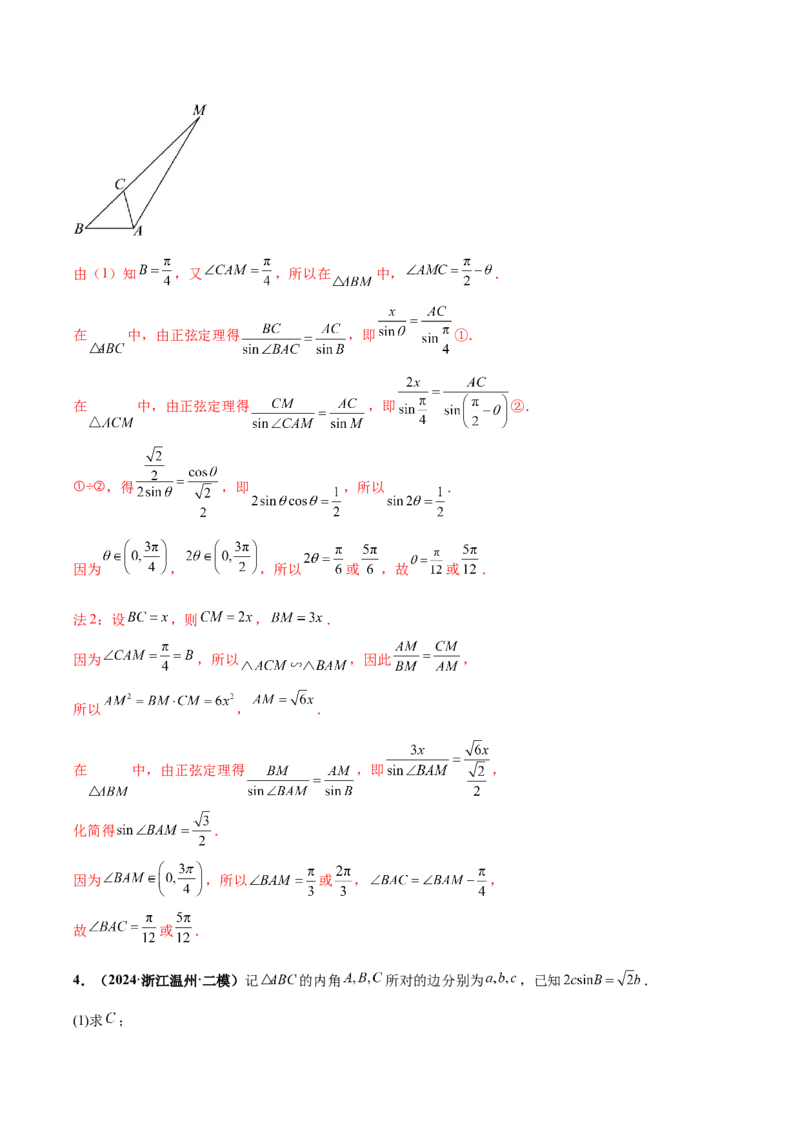
3.(2024·江苏·一模)在 中, .
(1)求B的大小;
(2)延长BC至点M,使得 .若 ,求 的大小.
【答案】(1) ;
(2) 或 .
【分析】(1)由 ,代入已知等式中,利用两角和与差的正弦公式化简得 ,可
得B的大小;
(2)设 , ,在 和 中,由正弦定理表示边角关系,化简求 的大小.
【详解】(1)在 中, ,所以 .
因为 ,所以 ,
即
化简得 .
因为 ,所以 , .
因为 ,所以 .
(2)法1:设 , ,则 .由(1)知 ,又 ,所以在 中, .
在 中,由正弦定理得 ,即 ①.
在 中,由正弦定理得 ,即 ②.
①÷②,得 ,即 ,所以 .
因为 , ,所以 或 ,故 或 .
法2:设 ,则 , .
因为 ,所以 ,因此 ,
所以 , .
在 中,由正弦定理得 ,即 ,
化简得 .
因为 ,所以 或 , ,
故 或 .
4.(2024·浙江温州·二模)记 的内角 所对的边分别为 ,已知 .
(1)求 ;(2)若 , ,求 的面积.
【答案】(1) 或
(2)
【分析】
(1)根据正弦定理,边化角,结合三角形中角的取值范围,可得 ,从而确定角 .
(2)根据条件求角求边,再结合三角形面积公式求面积.
【详解】(1)
由 得 ,而 为三角形内角,
故sinB>0,得 ,而 为三角形内角, 或
(2)
由 得 ,
又 ,∴ , ,故 ,
由(1)得 ,故 ,
∴ ,而 为三角形内角, ∴ .
又 即 ,
又 ,而 为三角形内角,故 ,
.
5.(2024·浙江嘉兴·二模)在 中,内角 所对的边分别是 ,已知 .
(1)求 的值;(2)若 为锐角三角形, ,求 的值.
【答案】(1) 或 ;
(2) .
【分析】(1)根据题意,利用二倍角余弦公式化简求解;
(2)解法一,由 ,利用正弦定理边化角得 ,结合 和 ,化简
运算并结合平方关系求得答案;
解法二,根据条件利用余弦定理可得 ,再利用正弦定理边化角并结合条件求得答案.
【详解】(1)由题可得 ,即 ,
解得 或 .
(2)解法一:因为 ,由正弦定理得 ,即 ,
即 ,
因为 ,所以 ;
所以 ,又 ,
且 为锐角三角形,解得 .
解法二:由余弦定理得 ,因为 ,所以 ,即 ,
所以 ,所以 ,
又 ,所以 ,所以 .
6.(2023·福建福州·模拟预测)在 中,角 的对边分别是 ,且 .(1)求 ;
(2)若 面积为 ,求 边上中线的长.
【答案】(1)
(2)
【分析】(1)由正弦定理边化角即可得到角 ;
(2)根据 ,得 ,结合三角形面积公式即可得到 ,再由正弦定理得边c,以及
,即可得到答案.
【详解】(1) ,由正弦定理边化角得 ,
, ,
或 (舍),
又 , ;
(2) , , , ,
,即 ,解得 ,
由正弦定理 ,
得 ,
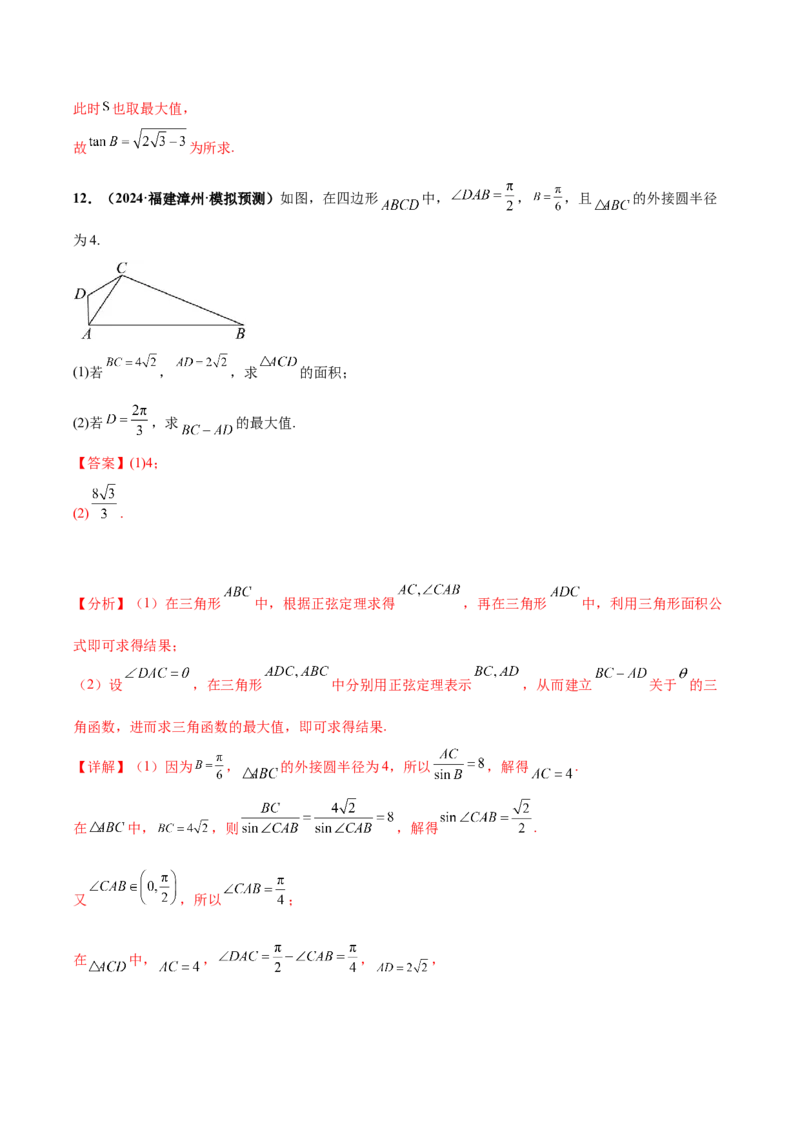
设 边的中点为 ,连接 ,如下图:,即 ,
即 ,
解得 .
7.(2024·山东淄博·一模)如图,在△ABC中, 的角平分线交 BC于P点, .
(1)若 ,求△ABC的面积;
(2)若 ,求BP的长.
【答案】(1)
(2)
【分析】(1)利用余弦定理和三角形面积公式即可求出答案;
(2)首先利用余弦定理求出 ,再利用正弦定理求出 ,再根据三角恒变换求出 ,最后
再根据正弦定理即可.
【详解】(1) 中,设角A、B、C的对边分别为 、 、 ,
在 中由余弦定理得 ,
即 ①
因 ,即 ,整理得 ②
①②解得 ,
所以 .
(2)因为 ,
所以在 中由余弦定理可得 ,
所以
解得 ,
由正弦定理得 ,
即 ,解得 ,
所以 ,
中由正弦定理得 ,则 ,
解得 ,
所以 .
8.(2024·安徽·模拟预测)如图,在平面四边形ABCD中, , .(1)若 , ,求 的值;
(2)若 , ,求四边形ABCD的面积.
【答案】(1)
(2)
【分析】(1) 中求出 ,在 中,由正弦定理求出 的值;
(2) 和 中,由余弦定理求出 和 ,得 和 ,进而可求四边形ABCD的面
积.
【详解】(1)在 中, , ,则 ,
,
在 中,由正弦定理得 ,
.
(2)在 和 中,由余弦定理得
,
,
得 ,又 ,得 ,
则 , ,
四边形ABCD的面积.
9.(2024·浙江·一模)在 中,内角 所对的边分别是 ,已知 .
(1)求角 ;
(2)设边 的中点为 ,若 ,且 的面积为 ,求 的长.
【答案】(1)
(2)
【分析】(1)根据正弦定理和题中所给式子化简计算得到 ,再结合余弦定理即可求出角 ;
(2)根据三角形面积公式得到 和 ,再结合中线向量公式计算即可.
【详解】(1)在 中,由正弦定理得, ,
因为 ,所以 ,
化简得, ,
在 中,由余弦定理得, ,
又因为 ,所以
(2)由 ,得 ,
由 ,得 ,所以 .
又因为边 的中点为 ,所以 ,
所以10.(2024·湖北·一模)在 中,已知 .
(1)求 的大小;
(2)若 ,求函数 在 上的单调递增区间.
【答案】(1) 或
(2)
【分析】(1)利用正弦定理及三角函数的特殊值对应特殊角即可求解;
(2)利用大边对大角及三角形的内角和定理,再利用诱导公式及三角函数的性质即可求解.
【详解】(1)在 中,由正弦定理可得:
,即 ,解得 ,
又 ,故 或 .
(2)由 ,可得 ,故 .
,
令 ,解得 .
由于 ,取 ,得 ;取 ,得 ;取 ,得 ,
故 在 上的单调递增区间为 .
11.(2024·福建厦门·二模)定义:如果三角形的一个内角恰好是另一个内角的两倍,那么这个三角形叫
做倍角三角形.如图, 的面积为 ,三个内角 所对的边分别为 ,且 .(1)证明: 是倍角三角形;
(2)若 ,当 取最大值时,求 .
【答案】(1)证明见解析
(2)
【分析】(1)由三角形面积公式化简条件,结合余弦定理及正弦定理进一步化简即可证明;
(2)由正弦定理结合题中条件得到 ,结合三角形面积公式 化为关于 的表
达式,构造函数,利用导数求得最大值即可.
【详解】(1)因为 ,
又 ,所以 ,
则 ,
又由余弦定理知, ,
故可得 ,
由正弦定理, ,
又 ,
代入上式可得 ,
即 ,
,
则有 ,
故 是倍角三角形.
(2)因为 ,所以 ,故 ,则 ,又 ,
又 ,则 ,
则
,
设 , ,
则
令 得 或者 (舍),
且当 时, ,
当 时, ,
则 在 上单调递增,
在 上单调递减,
故当 时, 取最大值,此时 也取最大值,
故 为所求.
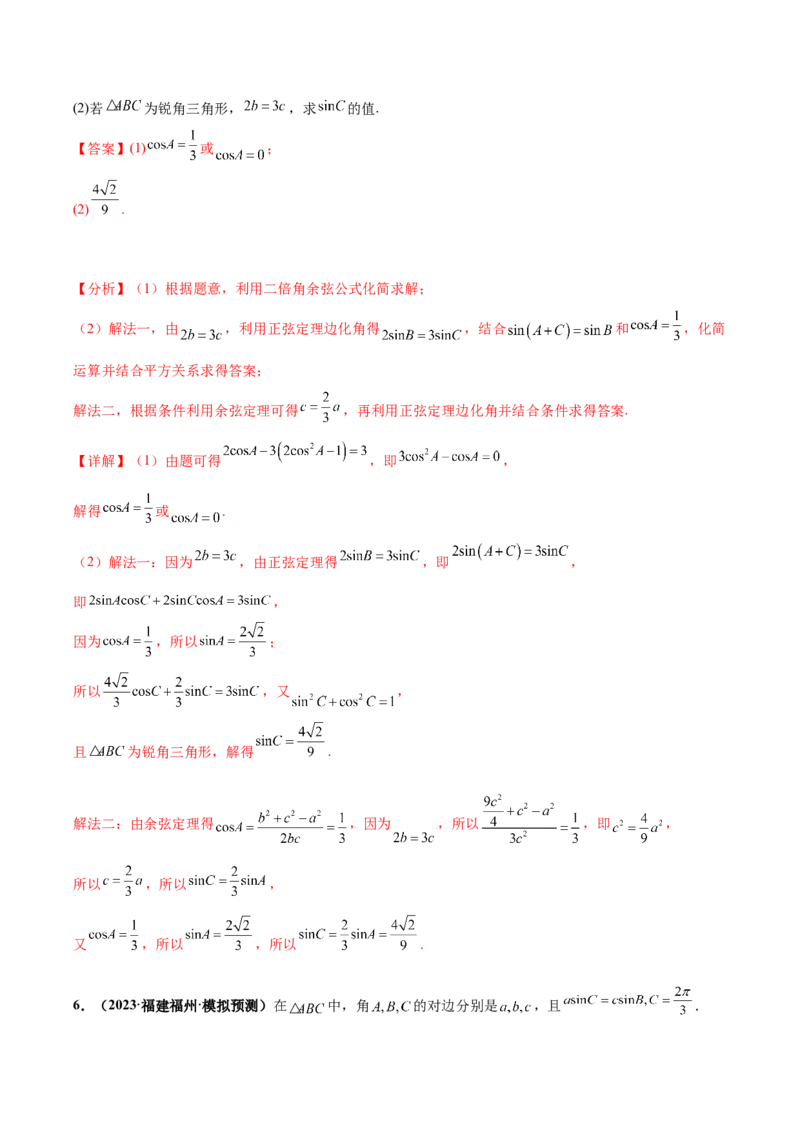
12.(2024·福建漳州·模拟预测)如图,在四边形 中, , ,且 的外接圆半径
为4.
(1)若 , ,求 的面积;
(2)若 ,求 的最大值.
【答案】(1)4;
(2) .
【分析】(1)在三角形 中,根据正弦定理求得 ,再在三角形 中,利用三角形面积公
式即可求得结果;
(2)设 ,在三角形 中分别用正弦定理表示 ,从而建立 关于 的三
角函数,进而求三角函数的最大值,即可求得结果.
【详解】(1)因为 , 的外接圆半径为4,所以 ,解得 .
在 中, ,则 ,解得 .
又 ,所以 ;
在 中, , , ,所以 .
(2)设 , .
又 ,所以 .
因为 ,所以 .
在 中, ,由正弦定理得 ,
即 ,解得
.
在 中, ,由正弦定理得 ,
即 ,解得 ,
所以 .
又 ,所以 ,
当且仅当 ,即 时, 取得最大值1,
所以 的最大值为 .
13.(2024·山东济南·二模)如图,在平面四边形ABCD中, , , ,
.(1)若 , ,求 的大小;
(2)若 求四边形ABCD面积的最大值.
【答案】(1)
(2)
【分析】(1)在 中,利用余弦定理可得 ,由等腰三角形可得 ,然后在
中利用正弦定理即可求解;
(2)利用勾股定理求得 ,然后四边形面积分成 即可求解.
【详解】(1)在 中, , ,所以 ,
由余弦定理可得, ,即 ,
又 ,所以 ,
在 中,由正弦定理可得 ,得 ,
因为 ,所以 ,所以 .
(2)在 中, ,所以 ,
所以,四边形ABCD的面积
,
当 时, ,即四边形ABCD面积的最大值为 .
14.(2024·湖北武汉·模拟预测)已知锐角 的三内角 的对边分别是 ,且,
(1)求角 的大小;
(2)如果该三角形外接圆的半径为 ,求 的取值范围.
【答案】(1)
(2)
【分析】(1)由余弦定理将 化成边,化简再结合余弦定理可求得答案;
(2)利用正弦定理,将边化角,再利用角的范围即可得出结果.
【详解】(1) ,
由余弦定理可得 ,
化简整理得 ,又 ,
,又 ,
所以 .
(2)因为三角形外接圆半径为 ,所以 , ,
,由(1)得 ,
所以,
因为 是锐角三角形,且 ,
所以 , , ,
,即 .
所以 的取值范围为 .
15.(2024·湖南邵阳·模拟预测)在 中,角 的对边分别为 ,且 的周长为
.
(1)求 ;
(2)若 , , 为边 上一点, ,求 的面积.
【答案】(1) ;
(2) .
【分析】(1)根据给定条件,利用正弦定理角化边,再利用余弦定理求解即得.
(2)由(1)的结论,利用三角形面积公式,结合割补法列式求出 ,再求出 的面积.
【详解】(1)在 中, ,由正弦定理得 ,
整理得 ,由余弦定理得 ,而 ,
所以 .
(2)由 为边 上一点, 及(1)得 ,且 ,即有 ,则 ,解得 ,
所以 的面积 .
16.(2024·广东梅州·二模)在 中,角A,B,C所对应的边分别为a,b,c,
, ,
(1)求A的大小:
(2)点D在BC上,
(Ⅰ)当 ,且 时,求AC的长;
(Ⅱ)当 ,且 时,求 的面积 .
【答案】(1)
(2) ;
【分析】(1)利用正弦定理,三角函数恒等变换的应用化简已知等式可得 的值,结合 即可
求解 的值;
(2)(Ⅰ)根据锐角三角函数和差角公式可得 正
弦定理即可求解.
(Ⅱ)采用面积分割的方法以及正弦定理即可解决.
【详解】(1)因为 ,
所以由正弦定理可得 ,又 ,
所以 ,
因为 为三角形内角, ,
所以 ,可得 ,
因为 ,所以 ;
(2)(Ⅰ)此时 , ,
所以 ,所以
,
在 中,由正弦定理可得 ;
(Ⅱ)设 ,由 ,
可得 ,化简可得
有 ,
由于 ,所以 ,
所以 ,
则 .
17.(2024·广东广州·一模)记 的内角 , , 的对边分别为 , , , 的面积为 .已知
.
(1)求 ;(2)若点 在边 上,且 , ,求 的周长.
【答案】(1) ;
(2)
【分析】(1)根据三角形面积公式和余弦定理,化简已知条件,结合 的范围,即可求得结果;
(2)利用平面向量的线性运算及数量积运算,求得 ,即可求得三角形周长.
【详解】(1)由 ,则 ,
又 ,故 .
(2)由(1)可知, ,又 ,则 ;
由题可知, ,
故 ,
所以 ,
因为 ,所以 , ,
在 中, ,
故 的周长为 .
18.(2024·广东佛山·模拟预测)在 中,角 所对的边分别为 ,其中 , .(1)求角 的大小;
(2)如图, 为 外一点, , ,求 的最大值.
【答案】(1)
(2)
【分析】
(1)根据题意,由正弦定理将边化为角,可得角的方程,化简计算,即可得到结果;
(2)根据题意,由正弦定理可得 ,再由余弦定理分别得到 ,再由基本不等式代
入计算,即可得到结果.
【详解】(1)因为 ,所以 ,
由正弦定理 ,可得 ,
整理可得 ,
又因为 ,
化简可得 ,
而 ,则 ,又 ,则
(2)在 中,由 可得 ,
在 中,由 可得 ,
所以 ,
设 ,
由余弦定理 ,
,
可得 , ,因此 ,
当且仅当 时,即 等号成立,
所以 的最大值为 ,此时 .
19.(2024·河北石家庄·二模)在 中,角A,B,C所对的边分别为a,b,c,设向量
, .
(1)求函数 的最大值;
(2)若 ,求 的面积.
【答案】(1)
(2)
【分析】(1)由平面向量的数量积与三角恒等变换知识计算可得 ,再结合三角函数的
值域计算即可求得;
(2)由题中条件计算可得 ,再由正弦定理得 ,由余弦定理可得 ,再由三角形的面积
公式计算即可求得.
【详解】(1)
因为 ,所以 ,
所以当 ,即 时, 有最大值 ;(2)因为 ,所以 ,所以 ,
因为 ,所以 ,
由正弦定理得: ,
所以 , ,
又因为 ,所以 ,
所以 ,
由余弦定理有: ,
即 ,所以 ,
所以 .
20 . ( 2024· 广 东 · 一 模 ) 设 锐 角 三 角 形 的 内 角 的 对 边 分 别 为 , 已 知
.
(1)求 ;
(2)若点 在 上(与 不重合),且 ,求 的值.
【答案】(1)
(2)
【分析】(1)根据条件,边转角得到 ,再利用
即可求出结果;
(2)根据题设得到 ,进而可求得 , ,再利用 ,即可求出结
果.
【详解】(1)由 ,得到 ,又 ,
所以 ,又三角形 为锐角三角形,所以 ,
得到 ,即 .
(2)因为 ,又 ,所以 ,则 ,所以
,
由(1)知, ,则 , ,
则 ,
又 ,所以 .
21.(2024·辽宁·二模)在 中, 为 边上一点, ,且 面积是 面积的2倍.
(1)若 ,求 的长;
(2)求 的取值范围.
【答案】(1)
(2)
【分析】(1)根据三角形面积公式,结合余弦定理进行求解即可;
(2)根据余弦定理、二倍角的余弦公式求出 的表达式,最后根据正弦定理求出 的表达式,
利用余弦函数的最值性质进行求解即可.【详解】(1)设 边上的高为 ,垂足为 ,
因为 面积是 面积的2倍,
所以有 ,
设 ,
由余弦定理可知:
,
解得 或 舍去,即 ;
(2)由(1)可知 ,
设 ,由 且 ,
由余弦定理可得:
,
,
在 中,因为 ,
所以由正弦定理可知:
,因为 ,
所以 ,
于是有 ,因此 的取值范围为 .
.
22.(2024·黑龙江齐齐哈尔·一模)记 的内角 的对边分别为 ,已知
.
(1)求 ;
(2)若 的面积为 ,求 边上的中线长.
【答案】(1)
(2) .
【分析】(1)利用正弦定理以及三角恒等变换的知识求得 .
(2)根据三角形 的面积求得 ,根据同角三角函数的基本关系式求得 ,利用正弦定理、
向量数量积运算来求得 边上的中线长.
【详解】(1)由正弦定理可得 ,所以 ,
即 ,又 ,
所以 ,
整理得 ,解得 ;(2)依题意, ,解得 ,
又 ,
所以 为钝角,所以由 ,
解得 ,
由正弦定理可得 ,又 ,
所以 ,
设 的中点为 ,则 ,
所以 ,
所以 边上的中线长为 .
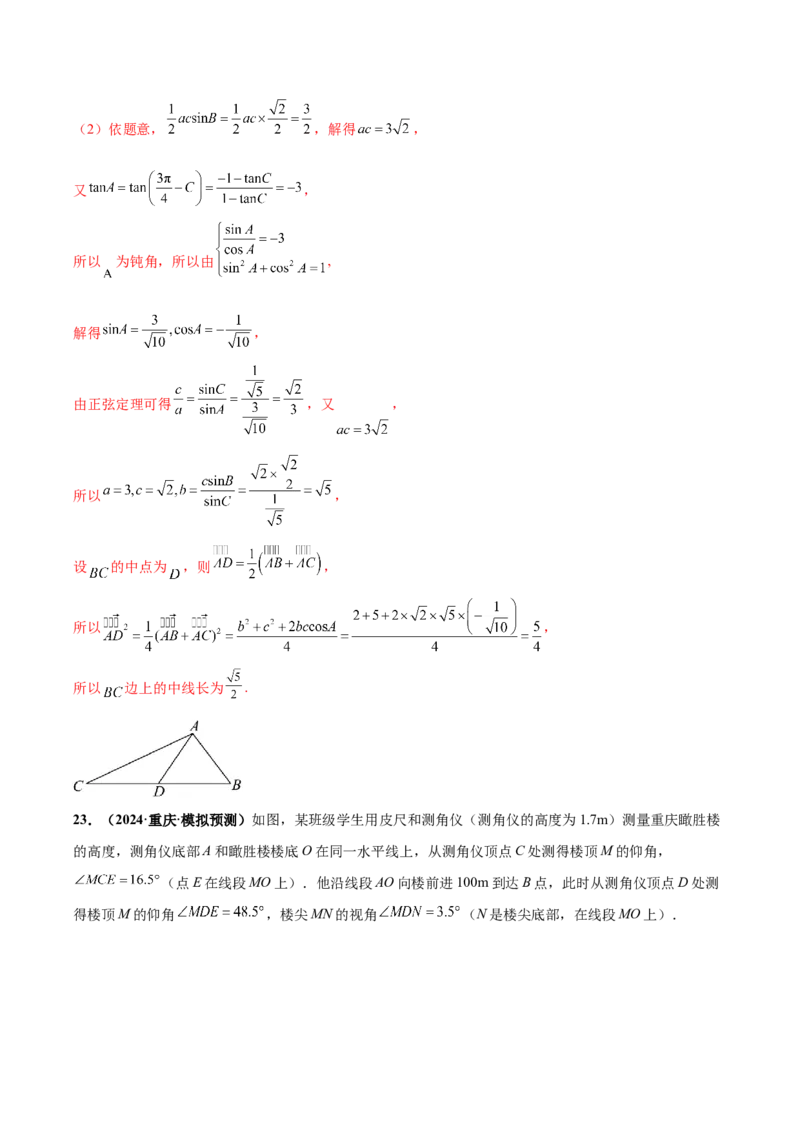
23.(2024·重庆·模拟预测)如图,某班级学生用皮尺和测角仪(测角仪的高度为1.7m)测量重庆瞰胜楼
的高度,测角仪底部A和瞰胜楼楼底O在同一水平线上,从测角仪顶点C处测得楼顶M的仰角,
(点E在线段MO上).他沿线段AO向楼前进100m到达B点,此时从测角仪顶点D处测
得楼顶M的仰角 ,楼尖MN的视角 (N是楼尖底部,在线段MO上).(1)求楼高MO和楼尖MN;
(2)若测角仪底在线段AO上的F处时,测角仪顶G测得楼尖MN的视角最大,求此时测角仪底到楼底的距
离FO.
参考数据: , , ,
【答案】(1) ,
(2)FO为37.4m
【分析】(1)法一:在 中,由正弦定理得,可得 ,进而求得 MO,进而求
得CE,计算可求得楼离MO和楼尖MN;
法二:利用 , ,可求得ME,进而计算可求得楼离MO和楼尖MN;
(2)设 , , ,进而可得
,利用基本不等式可求得楼尖MN的视角最大时x的值.
【详解】(1)法一: , ,∴ .
在 中,由正弦定理得, ,
又 ,∴ .
∴ ,∴ .
(m).
∴ .
∵ ,∴ , .
法二: , ,
∴ ,
即 ,∴ ,
∴ .
m.
∴ .
∵ ,∴ , .
(2)设 , , ,
∴
,
当且仅当 ,即 时,等号成立.
∴测角仪底到楼底的距离FO为37.4m处时,测得楼尖MN的视角最大.
24.(2024·重庆·模拟预测)在 中,内角A,B,C所对的边分别为a,b,c.已知
.
(1)求角A的大小;
(2)若 ,且 ,求AP的最小值.【答案】(1) ;
(2) .
【分析】(1)根据题意,由正弦定理代入计算,结合三角恒等变换公式代入计算,即可得到结果;
(2)根据题意,由平面向量数量积的运算律代入计算,结合基本不等式代入计算,即可得到结果.
【详解】(1)在 中,由正弦定理 ,可得
又由 知 ,
即 ,得 ,得 ,
得 ,所以 ;
又因为 ,所以 .
(2)由 ,得 ,
所以
,
当且仅当 ,即 时等号成立,故AP的最小值为 .
25.(2024·山西朔州·一模)已知 的内角 的对边分别为 ,向量,且 .
(1)求 ;
(2)求 的最小值.
【答案】(1)
(2)
【分析】(1)利用向量共线的坐标形式可得 ,结合余弦定理可求 ;
(2)利用基本不等式可求最小值.
【详解】(1)因为 ,所以 ,
由正弦定理可得 即 ,
故 ,所以 ,
而 为三角形内角,故 .
(2)结合(1)可得: ,
,当且仅当 时等号成立,
故 的最小值为 .
26.(2024·河南开封·二模)记 的内角A,B,C的对边分别为a,b,c,已知 .
(1)求 ;
(2)若 ,再从条件①,条件②,条件③中选择一个条件作为已知,使其能够确定唯一的三角形,并求
的面积.条件① : ;条件② : ;条件③ : .
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个
解答计分.
【答案】(1) ;
(2)答案见解析.
【分析】(1)利用正弦定理边化角,结合同角公式计算即得.
(2)选择条件①,利用余弦定理及三角形面积公式计算求解;选择条件②,利用正弦定理计算判断三角
形不唯一;选择条件③,利用正弦定理计算判断,再求出三角形面积.
【详解】(1)由 得: ,而 ,
则 , 为锐角,又 ,解得 ,
所以 且 为锐角.
(2)若选条件①,由 , 为锐角,得 ,
由余弦定理得 ,又 ,则 ,
解得 唯一确定,所以 .
若选条件②,由正弦定理得 ,则 ,
由 ,得 ,因此角 有两解,分别对应两个三角形,不符合题意.
若选条件③,由 , 为锐角,得 ,又 ,得 , ,则 ,
因此 唯一确定,
由正弦定理得 ,则 ,所以 .
27.(2024·河南·一模) 中,角A,B,C的对边分别为a,b,c,且满足 .
(1)求证: ;
(2)若 为锐角三角形,求 的取值范围.
【答案】(1)证明见解析
(2)
【分析】(1)用正弦定理边化角,再利用和差化积公式与诱导公式进行化简,得 ,从而
用等量关系即可得证;
(2)由(1)知,锐角三角形 中 ,利用角 关系求得角 的范围,再把式子
用角 的三角函数来表示并利用两角和差的正弦公式进行化简,进而用三角函数的取值
范围即可求解.
【详解】(1)证明:由条件 ,根据正弦定理可得 ,
,即 ,
,
又 中 ,进行化简得 ,
所以 ,即 或 ,即 (舍去),
所以 .
(2)若 为锐角三角形,根据(1) ,
则 ,得 ,
式子 , ,
由 得 ,又易知函数 在 内单调递减,
所以 ,
因此 .
28.(2023·河南·三模)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知 ,
且 .
(1)求证: ;
(2)若 的平分线交AC于D,且 ,求线段BD的长度的取值范围.
【答案】(1)证明见解析
(2)
【分析】(1)根据正余弦定理边角互化可得 ,即可利用三函数的性质求解,
(2)根据正弦定理以及角的范围即可利用三角函数的范围求解.
【详解】(1)证明:由余弦定理可得 ,
故 ,由正弦定理得 .
所以在 中, 或 .
若 ,又 ,故 ,因为 ,所以 ,故 不满足题意,舍去,
所以 .(2)在 中,
由正弦定理可得 ,即
所以
因为 是锐角三角形,且 ,
所 得 ,
所以 .
所以线段BD长度的取值范围是 .
29.(2024·湖北·二模)已知 的内角A,B,C的对边分别为a,b, ,
.
(1)求A;
(2)者 , ,求 的取值范围.
【答案】(1)
(2)
【分析】(1)借助正弦定理、三角形内角和与两角差的正弦公式计算即可得;
(2)借助向量的模长与平方的关系,结合数量积公式计算可得 ,借助三角函数的性质,可令 , ,结合余弦定理计算可得 ,即可得解.
【详解】(1)由正弦定理得 ,
则 ,
则 , , .
即 或 ,解得 或 .
因为 ,所以 ,所以 舍去,即 ;
(2)由 得 ,则 ,
则 ,
则 ,则 ,即 .
令 , ,因为 , ,所以 .
因为 ,所以 ,解得 .
由(1)得 ,则 ,
又因为 .所以 ,所以7 ,
解得 ,所以 ,解得 ,
所以 .
令 ,则 ,则 .
因为 ,所以 ,即 .
30.(2024·河北·二模)若 内一点 满足 ,则称点 为 的布洛卡点,
为 的布洛卡角.如图,已知 中, , , ,点 为的布洛卡点, 为
的布洛卡角.(1)若 ,且满足 ,求 的大小.
(2)若 为锐角三角形.
(ⅰ)证明: .
(ⅱ)若 平分 ,证明: .
【答案】(1)
(2)(ⅰ)证明见解析;(ⅱ)证明见解析.
【分析】(1)先判断 与 相似,进而得到 ,应用余弦定理求出 的值即可;
(2)(ⅰ)在 内,三次应用余弦定理以及三角形的面积公式得:
,针对 分别在 、 和 内,三次应用余弦
定理以及三角形的面积公式,且 表示出三角形的面积,由余弦定理形式相加,
再化简整理得: ,即可得证;(ⅱ)得出 与 的等量关系,再利用余弦定
理和三角形的面积公式, 平分 ,将 代入,化简整理即可得证.
【详解】(1)若 ,即 ,得 ,
点 满足 ,则 ,在 和 中, , ,
所以 与 相似,且 ,
所以 ,即 ,
由余弦定理得: ,且 , ,
得 ,且 ,
所以 ;
(2)(ⅰ)在 内,应用余弦定理以及三角形的面积公式得:
,
,
,
三式相加可得: ①
在 内,应用余弦定理以及三角形的面积公式得:
,
在 和 内,同理: , ,
三式相等: ,
因为 ,由等比性质得:②
由①②式可证得: ;
(ⅱ)因为 ,
即 ,
所以 ,
在 中,
分别由余弦定理得: , ,
,
三式相加整理得 ,
,
将 代入得:
若 平分 ,则 , ,
所以 ③
又由余弦定理可得: ④
由③-④得:
所以 ,
所以 .
【点睛】关键点点睛:根据 表示出三角形得面积,在 中,由余弦定理相加,得出 与 的等量关系,是解决本题的关键.