文档内容
A级:“四基”巩固训练
一、选择题
1.已知集合S={a,b,c}中的三个元素是△ABC的三边长,那么△ABC一
定不是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
答案 D
解析 因为集合S={a,b,c}中的元素是△ABC的三边长,由集合元素的互
异性可知a,b,c互不相等,所以△ABC一定不是等腰三角形,故选D.
2.下列集合的表示方法正确的是( )
A.第二、四象限内的点集可表示为{(x,y)|xy≤0,x∈R,y∈R}
B.不等式x-1<4的解集为{x<5}
C.{全体整数}
D.实数集可表示为R
答案 D
解析 A项中应是xy<0;B项中的本意是想用描述法表示,但不符合描述法
的规范格式,缺少了竖线和竖线前面的代表元素 x,应为{x|x<5};C项中的“{
}”与“全体”意思重复.故选D.
3.下列集合恰有两个元素的是( )
A.{x2-x=0} B.{x|y=x2-x}
C.{y|y2-y=0} D.{y|y=x2-x}
答案 C
解析 A项为一个方程集,只有一个元素;B项为方程y=x2-x的定义域,
有无数个元素;C项为方程y2-y=0的解,有0,1两个元素;D项为函数y=x2-
x的值域,有无数个元素.故选C.
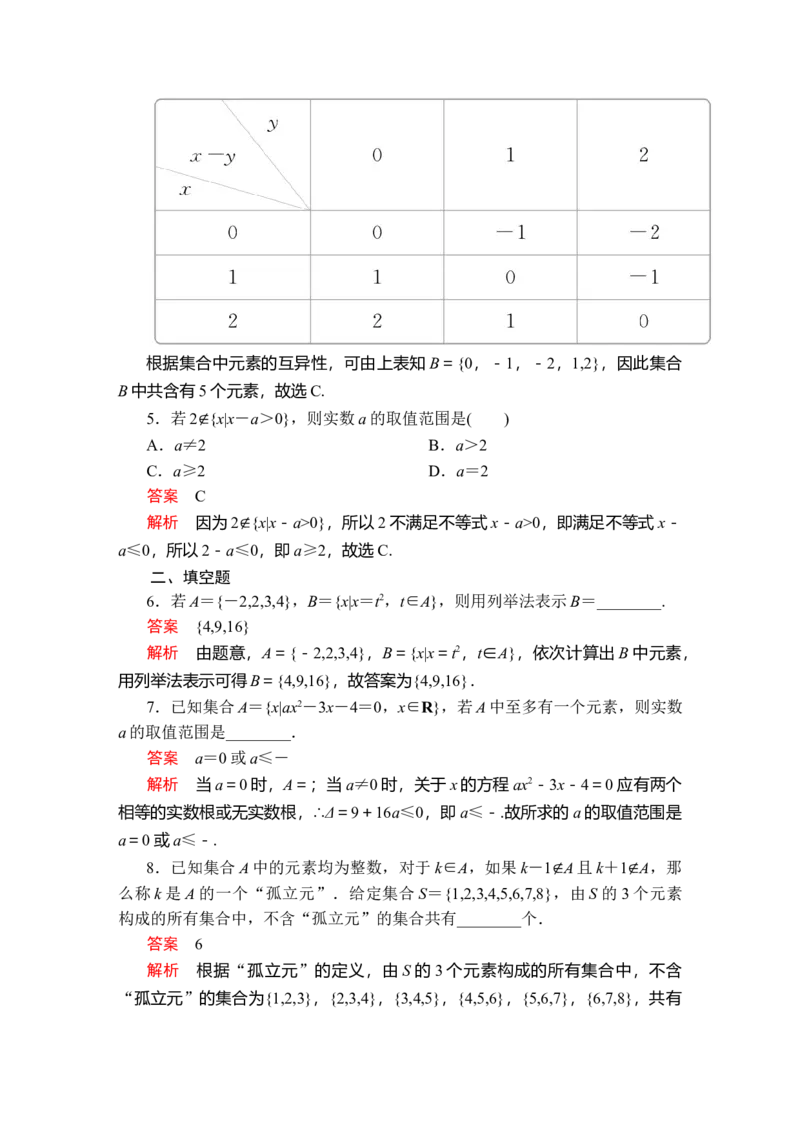
4.已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是(
)
A.1 B.3
C.5 D.9
答案 C
解析 根据已知条件,列表如下:根据集合中元素的互异性,可由上表知 B={0,-1,-2,1,2},因此集合
B中共含有5个元素,故选C.
5.若2∉{x|x-a>0},则实数a的取值范围是( )
A.a≠2 B.a>2
C.a≥2 D.a=2
答案 C
解析 因为2∉{x|x-a>0},所以2不满足不等式x-a>0,即满足不等式x-
a≤0,所以2-a≤0,即a≥2,故选C.
二、填空题
6.若A={-2,2,3,4},B={x|x=t2,t∈A},则用列举法表示B=________.
答案 {4,9,16}
解析 由题意,A={-2,2,3,4},B={x|x=t2,t∈A},依次计算出B中元素,
用列举法表示可得B={4,9,16},故答案为{4,9,16}.
7.已知集合A={x|ax2-3x-4=0,x∈R},若A中至多有一个元素,则实数
a的取值范围是________.
答案 a=0或a≤-
解析 当a=0时,A=;当a≠0时,关于x的方程ax2-3x-4=0应有两个
相等的实数根或无实数根,∴Δ=9+16a≤0,即a≤-.故所求的a的取值范围是
a=0或a≤-.
8.已知集合A中的元素均为整数,对于 k∈A,如果k-1∉A且k+1∉A,那
么称k是A的一个“孤立元”.给定集合S={1,2,3,4,5,6,7,8},由S的3个元素
构成的所有集合中,不含“孤立元”的集合共有________个.
答案 6
解析 根据“孤立元”的定义,由 S的3个元素构成的所有集合中,不含
“孤立元”的集合为{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8},共有6个.故答案为6.
三、解答题
9.用适当的方法表示下列集合:
(1)绝对值不大于3的偶数的集合;
(2)被3除余1的正整数的集合;
(3)一次函数y=2x-3图象上所有点的集合;
(4)方程组的解集.
解 (1){-2,0,2}.
(2){m|m=3n+1,n∈N}.
(3){(x,y)|y=2x-3}.
(4){(0,1)}.
10.已知集合A={a+3,(a+1)2,a2+2a+2},若1∈A,求实数a的值.
解 ①若a+3=1,则a=-2,
此时A={1,1,2},不符合集合中元素的互异性,舍去.
②若(a+1)2=1,则a=0或a=-2.
当a=0时,A={3,1,2},满足题意;
当a=-2时,由①知不符合条件,故舍去.
③若a2+2a+2=1,则a=-1,
此时A={2,0,1},满足题意.
综上所述,实数a的值为-1或0.
B级:“四能”提升训练
1.已知集合A={x|x=3n+1,n∈Z},B={x|x=3n+2,n∈Z},M={x|x=
6n+3,n∈Z}.
(1)若m∈M,则是否存在a∈A,b∈B,使m=a+b成立?
(2)对于任意a∈A,b∈B,是否一定存在m∈M,使a+b=m?证明你的结论.
解 (1)设m=6k+3=3k+1+3k+2(k∈Z),
令a=3k+1,b=3k+2,则m=a+b.
故若m∈M,则存在a∈A,b∈B,使m=a+b成立.
(2)不一定.证明如下:
设a=3k+1,b=3l+2,k,l∈Z,则 a+b=3(k+l)+3.
当k+l=2p(p∈Z)时,a+b=6p+3∈M,此时存在m∈M,使a+b=m成立;
当k+l=2p+1(p∈Z)时,a+b=6p+6∉M,此时不存在m∈M,使a+b=m成
立.
故对于任意a∈A,b∈B,不一定存在m∈M,使a+b=m.
2.设实数集S是满足下面两个条件的集合:①1∉S;②若a∈S,则∈S.
(1)求证:若a∈S,则1-∈S;
(2)若2∈S,则S中必含有其他的两个数,试求出这两个数;
(3)求证:集合S中至少有三个不同的元素.
解 (1)证明:∵1∉S,∴0∉S,即a≠0.由a∈S,则∈S可得∈S,
即==1-∈S.
故若a∈S,则1-∈S.
(2)由2∈S,知=-1∈S;由-1∈S,知=∈S,当∈S时,=2∈S,
因此当2∈S时,S中必含有-1和.
(3)证明:由(1),知a∈S,∈S,1-∈S.
下证:a,,1-三者两两互不相等.
①若a=,则a2-a+1=0,无实数解,
∴a≠;
②若a=1-,则a2-a+1=0,无实数解,
∴a≠1-;
③若=1-,则a2-a+1=0,无实数解,
∴≠1-.
综上所述,集合S中至少有三个不同的元素.