文档内容
A级:“四基”巩固训练
一、选择题
1.设集合U={1,2,3,4,5,6},A={1,3,5},B={3,4,5},则 ∁U (A∪B)=( )
A.{2,6} B.{3,6}
C.{1,3,4,5} D.{1,2,4,6}
答案 A
解析 因为 A={1,3,5},B={3,4,5},所以 A∪B={1,3,4,5},因为 U=
{1,2,3,4,5,6},则∁U (A∪B)={2,6},故选A.
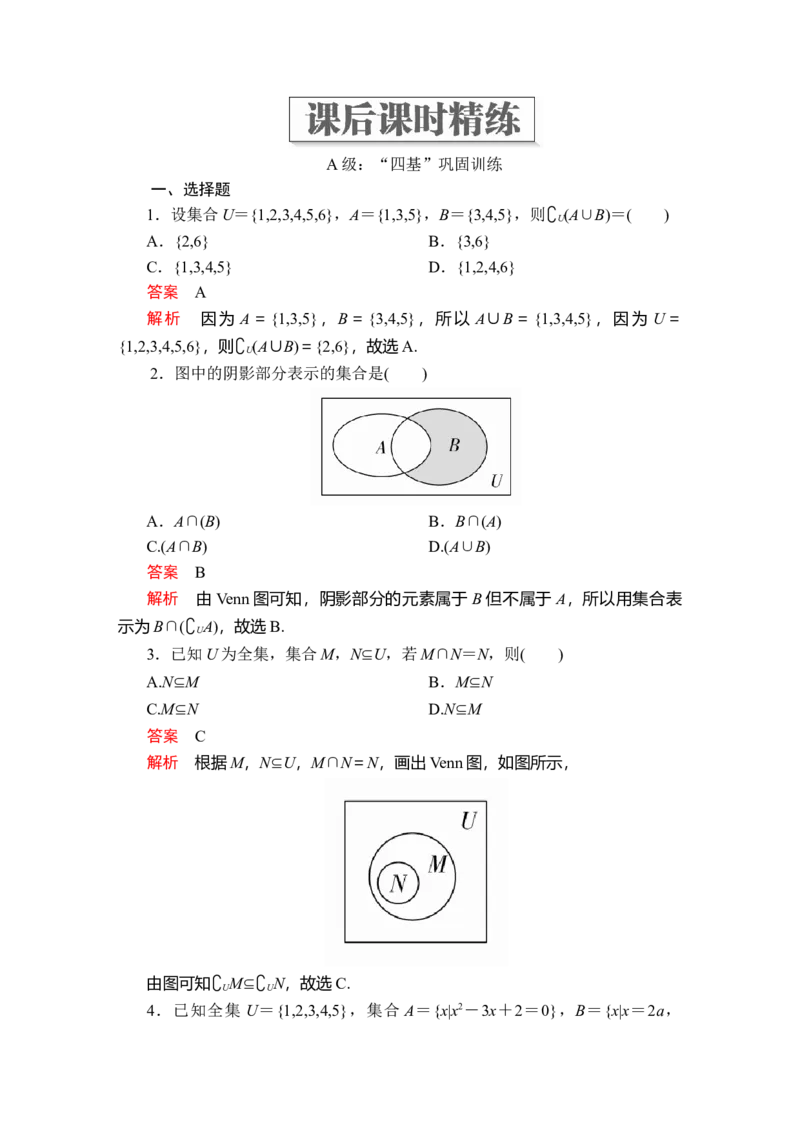
2.图中的阴影部分表示的集合是( )
A.A∩(B) B.B∩(A)
C.(A∩B) D.(A∪B)
答案 B
解析 由Venn图可知,阴影部分的元素属于 B但不属于A,所以用集合表
示为B∩(∁U A),故选B.
3.已知U为全集,集合M,N⊆U,若M∩N=N,则( )
A.N⊆M B.M⊆N
C.M⊆N D.N⊆M
答案 C
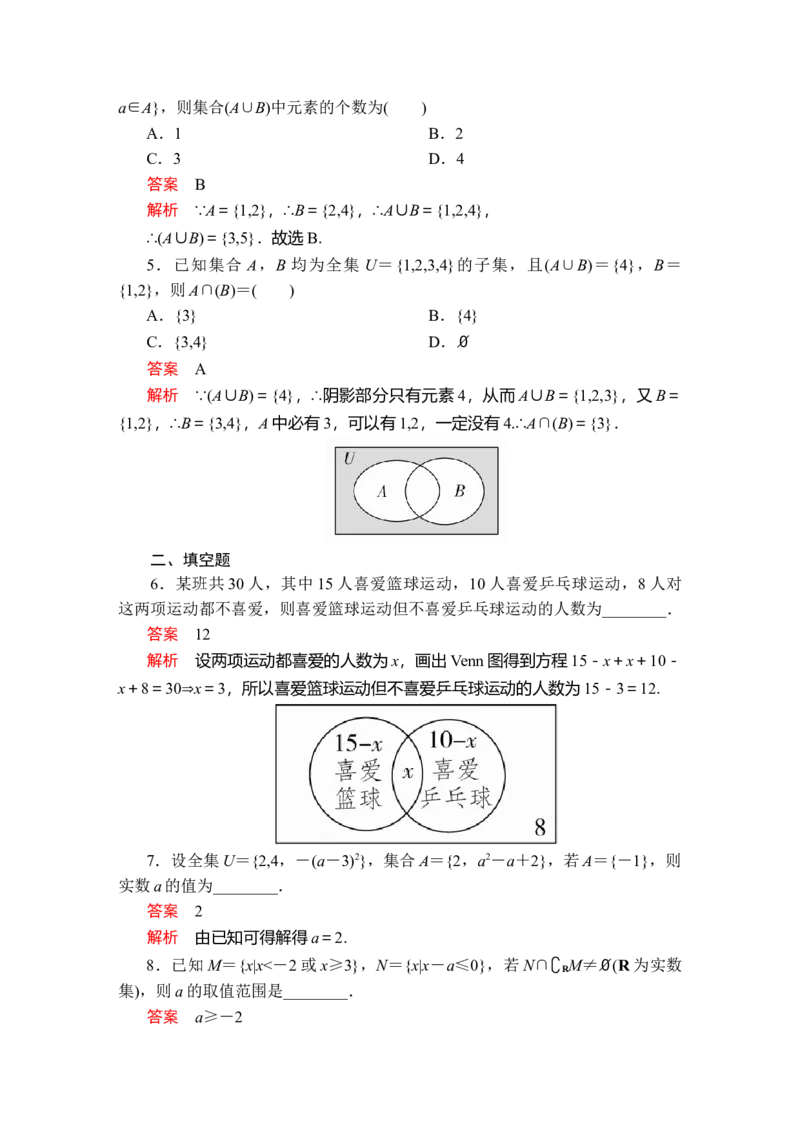
解析 根据M,N⊆U,M∩N=N,画出Venn图,如图所示,
由图可知∁U M⊆∁U N,故选C.
4.已知全集 U={1,2,3,4,5},集合 A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合(A∪B)中元素的个数为( )
A.1 B.2
C.3 D.4
答案 B
解析 ∵A={1,2},∴B={2,4},∴A∪B={1,2,4},
∴(A∪B)={3,5}.故选B.
5.已知集合 A,B 均为全集 U={1,2,3,4}的子集,且(A∪B)={4},B=
{1,2},则A∩(B)=( )
A.{3} B.{4}
C.{3,4} D.∅
答案 A
解析 ∵(A∪B)={4},∴阴影部分只有元素4,从而A∪B={1,2,3},又B=
{1,2},∴B={3,4},A中必有3,可以有1,2,一定没有4.∴A∩(B)={3}.
二、填空题
6.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对
这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为________.
答案 12
解析 设两项运动都喜爱的人数为x,画出Venn图得到方程15-x+x+10-
x+8=30⇒x=3,所以喜爱篮球运动但不喜爱乒乓球运动的人数为15-3=12.
7.设全集U={2,4,-(a-3)2},集合A={2,a2-a+2},若A={-1},则
实数a的值为________.
答案 2
解析 由已知可得解得a=2.
8.已知M={x|x<-2或x≥3},N={x|x-a≤0},若N∩
∁R
M≠∅(R为实数
集),则a的取值范围是________.
答案 a≥-2解析 ∵M={x|-2≤x<3},借助数轴 可得a≥
-2.三、解答题
9.已知全集 U={x|x≤4},集合 A={x|-22a-1,则a<2,
此时∁U B=R,∴A⊆∁U B;
若B≠∅,则a+1≤2a-1,即a≥2,
此时∁U B={x|x2a-1},
由于A⊆∁U B,∴或
解得a>4,
∴综上,实数a的取值范围为{a|a<2或a>4}.
B级:“四能”提升训练
1.若三个关于x的方程x2-2x-3-2a=0,x2-(a+2)x+a2=0,x2+x-3a
=0中至多有两个方程有实根,求实数a的取值范围.
解 设已知三个方程都有实根,此时a的取值范围为集合A.
则
⇒⇒a≥-.
∴A=.
∴三个方程中至多有两个方程有实根的a的取值范围是A的补集,即.
2.设 U=R,集合 A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0}.若(∁U A)∩B=∅,求m的值.
解 A={-2,-1},由(∁U A)∩B=∅,得B⊆A,
∵方程x2+(m+1)x+m=0的判别式Δ=(m+1)2-4m=(m-1)2≥0,
∴B≠∅.
∴B={-1}或B={-2}或B={-1,-2}.
①若B={-1},则m=1;
②若B={-2},则应有-(m+1)=(-2)+(-2)=-4,且m=(-2)×(-2)=
4,这两式不能同时成立,
∴B≠{-2};
③若 B={-1,-2},则应有-(m+1)=(-1)+(-2)=-3,且 m=(-
1)×(-2)=2,由这两式得m=2.经检验知m=1或m=2符合条件.
综上可得m=1或m=2.