文档内容
2024-2025 学年海南省先锋联盟高一上学期 11 月期中调研数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.集合 , ,则 ( )
A={x∈N|−√30,y>0),若x+2y>m2+2m恒成立,则实数m的取值范围是( )
x y
A. −40时,若方程f (x)=k(x+2)(k>0)有两个实根,则a=k±2√2k
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知a,b,c∈R,则下列命题为真命题的是( )
1 1
A. 若a>|b|,则a2>b2 B. 若a<|b|,则 >
a2 b2
c c 1 1
C. 若a>b>0,c<0,则 > D. 若a>b>c,则 >
a b a−c b−c
1
10.已知函数f (x)是定义在R上的奇函数,当x>0时,f (x)=x+ ,则以下说法中正确的是( )
x+a
1
A. f (0)=
a
5
B. 若f (−2)=− ,则a=0
2
C. 若a=−4,则函数f (x)在区间(4,+∞)上有最大值6
D. 若a=2,则函数f (x)在R上单调递增
11.对∀x∈R,[x]表示不超过x的最大整数,如[1.41]=1,[−2.57]=−3,我们把y=[x],x∈R叫做
取整函数,也称为高斯函数.以下关于“高斯函数”的命题,其中是真命题的有( )
A. 若{x}=x−[x],则{x}∈(0,1)
B. 对 ,有 [ 1 ] [ 1] [ 3 ] [ 9 ] 成立
∀x∈R [x]+ x+ + x+ + x+ +⋯+ x+ =[10x]
10 5 10 10
C. 不等式 的解集为
6[x] 2+7[x]−3≥0 (−∞,−1)∪[1,+∞)
1
D. 若函数f (x)=[x] 2 − [x]+1,则f (x)≥1
2
三、填空题:本题共3小题,每小题5分,共15分。
12.写出同时满足以下条件的 一个函数f (x)的解析式为 .①定义域为R,②在(−∞,0)上是增函数,
③函数f (x+1)是偶函数.
第 页,共 页
2 113.已知幂函数 经过点 , {f (x),x≥2则 .
f (x) (4,2) g(x)= g[g(3)]=
−x3,x<2
14.已知函数
{2x2,x≥0,若对任意
,不等式 恒成立,则实数 的
f (x)= x∈[m,m+1] f (x2+m)≤16f (x) m
−x2,x<0
取值范围是 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知集合 ,集合 .
A={x|x2+2x−3≤0} B={x|−10解集为B,且a∈{−1,0,1},求b,c的值.
16.(本小题12分)
已知集合 { x−2 }, .
A= x| <0,x∈R B={x|k40)
x
的车辆当年能全部销售完.
(1)求出2024年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售量×售价−成本);
(2)2024年产量为多少百辆时,企业所获利润最大?并求出最大利润.
19.(本小题12分)
小明同学通过课外阅读了解到一元三次函数的图象均存在对称中心,而函数的图象关于(m,n)成中心对称
的充要条件是 是奇函数 若函数 .
y=f (x+m)−n . f (x)=ax3+bx2+cx(a≠0)
1
(1)若a= ,b=−1,c=−3,
3
①求函数f (x)的图象的对称中心(m,n).
f (x+Δx)−f (x)
②我们知道:设区间D⊆R,当x∈D,若∀Δx>0都有 >0,则f (x)在D上是增函数,
Δx
并且f (x)在关于x=m对称 区间上有相同的单调性.请依据以上知识,求出f (x)的单调递增区间.
(2)若函数y=f (x+3)是奇函数,解关于x的不等式f (x)>0.
第 页,共 页
4 1参考答案
1.A
2.D
3.B
4.C
5.B
6.B
7.A
8.D
9.AC
10.BD
11.BCD
12. 答案不唯一
f (x)=−(x−1) 2 ( )
13.−3√3
14.[ 1+√13]
0,
2
15.(1)
由已知得 , ,
A={x|−3≤x≤1}
∁
B={x|x≤−1或x≥3}
R
所以 , .
A∩B={x|−1k
1 1
②当B≠⌀时, k≥−1 ,解得 −1
实数 的取值范围为(1 ).
k ,2
2
解法二:由 知 ,
(1) A={x|−13k−1>−1
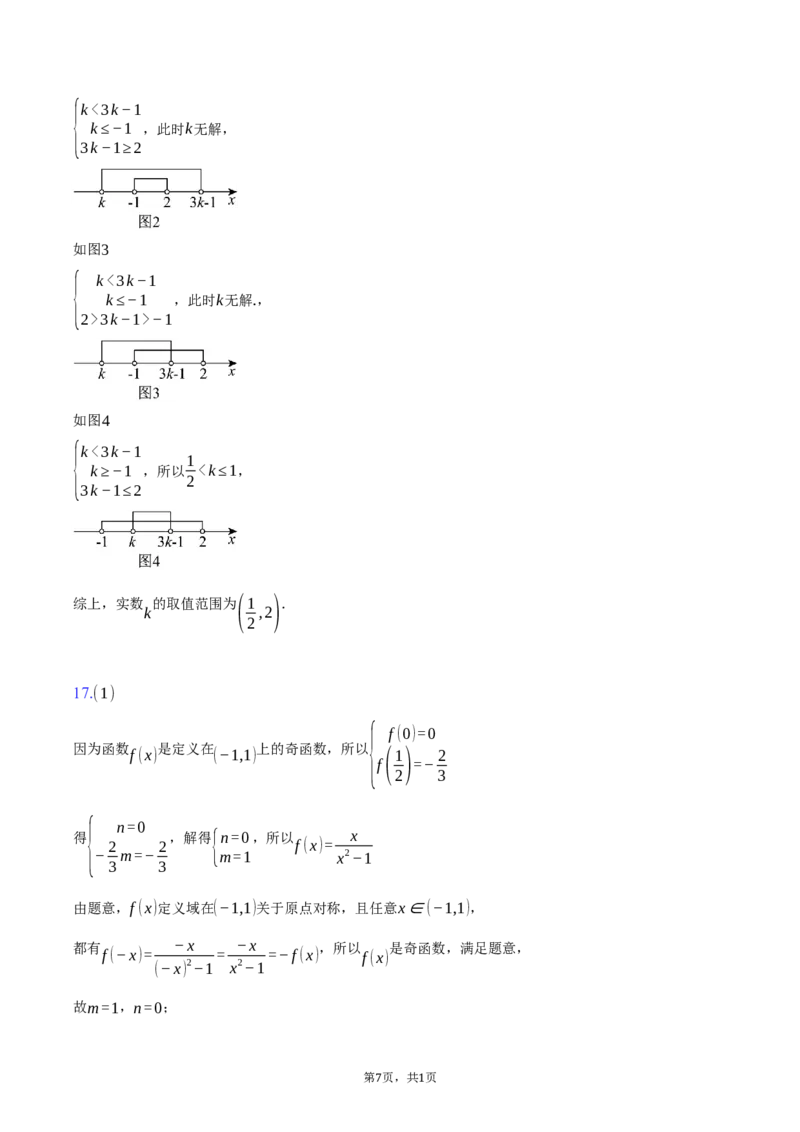
如图4
{k<3k−1
1
k≥−1 ,所以 0
1 2 1 2 1 2 2 1
,所以 ,所以 在 上是减函数.
(x2−1)(x2−1)>0 f (x )−f (x )>0 f (x) (−1,1)
1 2 1 2
(3)
f (t−1)+f (t2−1)<0⇔f (t−1)<−f (t2−1)
因为 是定义在 上的奇函数,所以
f (x) (−1,1) −f (t2−1)=f (1−t2)
x
f (t−1)1−t2 t>1或t<−2
故 的取值范围 .
t (1,√2)
18.(1)
每辆车售价9万元,年产量x(百辆)时销售收入为900x万元,
{10x2+100x+3000,(040)
x
{900x−(10x2+100x+3000),(040) = −4x− 8100 +14000,(x>45)
x x
(2)
第 页,共 页
8 1由 当 时, ,
(1) 013000万元,
所以年产量45百辆时利润最大,最大利润为13640万元.
19.(1)
1 1
①∵a= ,b=−1,c=−3,∴f (x)= x3−x2−3x,
3 3
设f (x)关于(m,n)中心对称,则y=f (x+m)−n为奇函数,
1
y=f (x+m)−n= (x+m) 3−(x+m) 2−3(x+m)−n
3
1 1
= x3+(m−1)x2+(m2−2m−3)x+ m3−m2−3m−n,
3 3
∵y=f (x+m)−n是奇函数,
1 11
则m−1=0, m3−m2−3m−n=0,解得m=1,n=− ,
3 3
所以 的对称中心为( 11);
f (x) 1,−
3
②∵f (x+Δx)−f (x)= 1 (x+Δx) 3−(x+Δx) 2−3(x+Δx)− (1 x3−x2−3x )
3 3
1
=(Δx)x2+((Δx) 2−2(Δx))x+ (Δx) 3−(Δx) 2−3(Δx),
3
f (x+Δx)−f (x) 1
∴ =x2+((Δx)−2)x+ (Δx) 2−(Δx)−3
Δx 3
1
=x2−2x−3+ (Δx) 2+(Δx)(x−1),
3
第 页,共 页
9 11
设g(Δx)=x2−2x−3+ (Δx) 2+(Δx)(x−1),
3
f (x+Δx)−f (x)
当x>1时,∵∀Δx>0都有 >0,
Δx
只需 , ,
g(0)=x2−2x−3>0 ∴x>3
∴当x>1时,f (x)的递增区间是(3,+∞),
又 的对称中心为( 11), 在 也递增,
∵f (x) 1,− ∴f (x) (−∞,−1)
3
∴f (x)的递增区间是(3,+∞),(−∞,−1);
(2)
因为函数y=f (x+3)是奇函数,所以f (x)图象关于(3,0)成中心对称,
所以f (3)=0,
又因为f (0)=0,所以f (6)=0,
所以f (x)=ax(x−3)(x−6),
∴不等式f (x)>0,即是ax(x−3)(x−6)>0,
当a>0时,有x(x−3)(x−6)>0,∴06,
此时,不等式解集为(0,3)∪(6,+∞);
当a<0时,有x(x−3)(x−6)<0,∴x<0或3