文档内容
第七章 随机变量及其分布(基础卷)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间1200分钟,试题共23题.答卷前,考生务必用0.5毫米黑色签字笔将
自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共12小题,每小题5分,共60分)在每小题所给出的四个选项中,只有一项是符合
题目要求的.
1.已知某离散型随机变量X服从的分布列如图,则随机变量X的方差D(X)等于( )
X 0 1
P m 2m
A. B. C. D.
2.将三颗骰子各掷一次,设事件A=“三个点数都不同”,B=“至少出现一个3点”,则条件概率P(A|
B),P(B|A)分别是( )
A. , B. , C. , D. ,
3.随机变量X的概率分布规律为P(X=n)= (n=1,2,3,4),其中a是常数,则P( <X< )的
值为( )
A. B. C. D.
4.已知离散型随机变量X服从二项分布X~B(n,p)且E(X)=12,D(X)=4,则n与p的值分别为
( )
A. B. C. D.
5.体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一
直发到3次为止.设学生一次发球成功的概率为 p (p≠0),发球次数为X,若X的数学期望EX>
1.75,则p的取值范围是( )
A.(0, ) B.( ,1) C.(0, ) D.( ,1)
6.设随机变量 ﹣N( ,1),若不等式 ≥0对任意实数x都成立,且P( >a)= ,则 的值为
( ) ξ μ ξ μ
A.0 B.1 C.2 D.3
7.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机抽取一件,其长度误差落
在区间(3,6)内的概率为( )
(附:若随机变量 服从正态分布N( ,σ2),则P( ﹣σ< < +σ)=68.26%,P( ﹣2σ< < +2σ)
ξ μ μ ξ μ μ ξ μ=95.44%)
A.4.56% B.13.59% C.27.18% D.31.74%
8.若随机变量X~N( ,σ2)(σ>0),则有如下结论:
高三(1)班有40名同μ 学,一次数学考试的成绩服从正态分布,平均分为120,方差为100,理论上说在
130分以上人数约为( )
A.19 B.12 C.6 D.5
9.设离散型随机变量X的分布列为
X 1 2 3
P P P P
1 2 3
则EX=2的充要条件是( )
A.P=P B.P=P C.P=P D.P=P=P
1 2 2 3 1 3 1 2 3
B.
10.口袋里放有大小相等的2个白球和1个红球,有放回地每次摸取1个球,定义数列{a}:a =
n n
如果S 为数列{a}的前n项和,那么S=5的概率为( )
n n 7
A. B.
C. D.
11.盒中有6个小球,其中4个白球,2个黑球,从中任取i(i=1,2)个球,在取出的球中,黑球放回,
白球则涂黑后放回,此时盒中黑球的个数X(i=1,2),则( )
i
A.P(X=3)>P(X=3),EX>EX B.P(X=3)<P(X=3),EX>EX
1 2 1 2 1 2 1 2
C.P(X=3)>P(X=3),EX<EX D.P(X=3)<P(X=3),EX<EX
1 2 1 2 1 2 1 2
12.我们知道,在n次独立重复试验(即伯努利试验)中,每次试验中事件A发生的概率为p,则事件A发
生的次数X服从二项分布B(n,p),事实上,在无限次伯努利试验中,另一个随机变量的实际应用也
很广泛,即事件A首次发生时试验进行的次数Y,显然P(Y=k)=p(1﹣p)k﹣1,k=1,2,3,…,
我们称Y服从“几何分布”,经计算得 .由此推广,在无限次伯努利试验中,试验进行到事件A和
都发生后停止,此时所进行的试验次数记为 Z,则P(Z=k)=p(1﹣p)k﹣1+(1﹣p)pk﹣1,k═2,
3,…,那么E(Z)=( )
A. B. C. D.二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线
上)
13.某地区空气质量监测资料表明,一天的空气质量为优良的概率是 ,连续两天为优良的概率是 ,已知某
天的空气质量为优良,则随后一天的空气质量为优良的概率是 .
14.下列随机变量中,不是离散型随机变量的是 .
①某地车展中,预定各类汽车的总人数X;
②北京故宫某周每天接待的游客人数;
③正弦曲线上的点P到x轴的距离X;
④小麦的亩产量X;
⑤王老师在一次英语课上提问的学生人数X.
15.已知随机变量 的分布列为:
ξ ﹣1 0 1 2
Pξ ﹣2a b
若 ,则a+b= ,D( )= .
ξ
16.甲、乙两名同学参加一项射击比赛游戏,其中任何一人射击一次击中目标得2分,未击中目标得0分.
若甲、乙两人射击的命中率分别为 和p,且甲、乙两人各射击一次得分之和为2的概率为 .假设甲、
乙两人射击互不影响,则p的值为 .
三、解答题(本大题共7小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过
程或演算步骤)
17.一袋中有6个黑球,4个白球.
(1)依次取出3个球,不放回,已知第一次取出的是白球,求第三次取到黑球的概率;
(2)有放回地依次取出3球,已知第一次取的是白球,求第三次取到黑球的概率;
(3)有放回地依次取出3球,求取到白球个数X的分布列.18.某中学随机抽取部分高一学生调查其每日自主安排学习的时间(单位:分钟),并将所得数据绘制成
如图所示的频率分布直方图,其中自主安排学习时间的范围是[0,100],样本数据分组为[0,20),
[20,40),[40,60),[60,80),[80,100].
(Ⅰ)求直方图中x 的值;
(Ⅱ)从学校全体高一学生中任选4名学生,这4名学生中自主安排学习时间少于20分钟的人数记为X,
求X的分布列和数学期望.(以直方图中的频率作为概率).
19.设从某地前往火车站,可乘公共汽车,也可乘地铁,若乘公共汽车所需时间(单位:min)X~N(50,
102),乘地铁所需时间Y~N(60,42),则
(1)若有70min可用,则乘公共汽车好还是乘地铁好?
(2)由于时间紧迫,决定做出租车去火车站,此时使用手机中打车软件甲,甲软件定位了 A公司2辆出
租车,B公司4辆出租车,每车被叫中的概率相等,甲软件能叫来两辆车,求A公司出租车被叫来的辆数
的分布列和数学期望 E( ).(已知 P( ﹣3σ<X≤ +3σ)=0.9974,P( ﹣2σ<X≤ +2σ)=
ɛ0.9544) ɛ μ μ μ μ20.甲、乙两人射击,甲射击一次中靶的概率是p,乙射击一次中靶的概率是p,且 , 是方程x2﹣5x+6=
1 2
0的两个实根,已知甲射击5次,中靶次数的方差是 .
(1)求p,p 的值;
1 2
(2)若两人各射击2次,至少中靶3次就算完成目的,则完成目的概率是多少?
(3)若两人各射击1次,至少中靶1次就算完成目的,则完成目的概率是多少?
21.某省高考曾经使用过一段标准分制度,标准分是把学生考试的基础分参与全省排出相对名称,通过公
式换算成标准分.高考后公布考生的标准分,而不公布基础分.考生根据自己的标准分多少就可以大
致估出自己在全省考生的名次.其标准分X是服从正态分布N(500,1002)的随机变量.假设某学生
的数学成绩不低于600的概率为p.
0
(Ⅰ)求p 的值;
0
(Ⅱ)某校高三的高考英语和数学两科都超过600分的有5人,仅单科超过600分的共有8人,在这些同
学中随机抽取3人,设三人中英语和数学双科都超过600分的有 人,求 的分布列和数学期望.
(参考数据:若X~N( ,σ2),有P( ﹣σ<X≤ +σ)=0.68ξ26,P(ξ ﹣2σ<X≤ +2σ)=0.9544,P
( ﹣3σ<X≤ +3σ)=0μ.9974.) μ μ μ μ
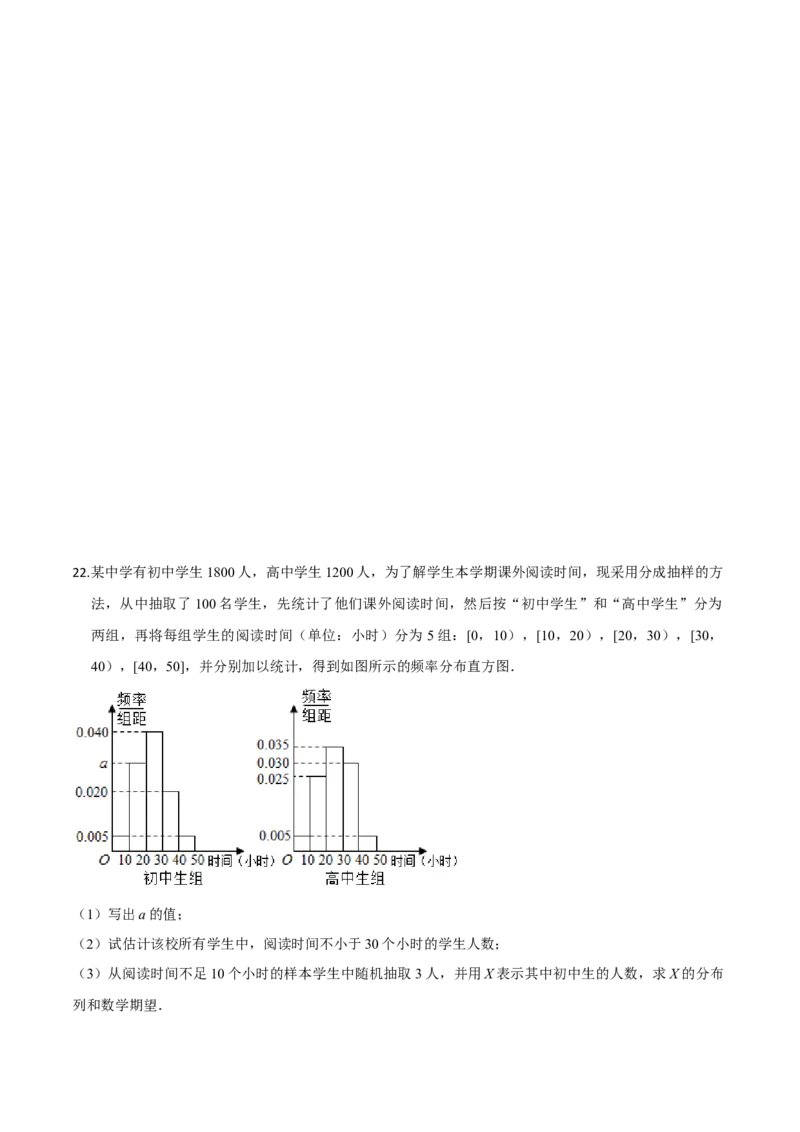
μ μ22.某中学有初中学生1800人,高中学生1200人,为了解学生本学期课外阅读时间,现采用分成抽样的方
法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为
两组,再将每组学生的阅读时间(单位:小时)分为 5组:[0,10),[10,20),[20,30),[30,
40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.
(1)写出a的值;
(2)试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(3)从阅读时间不足10个小时的样本学生中随机抽取3人,并用X表示其中初中生的人数,求X的分布
列和数学期望.