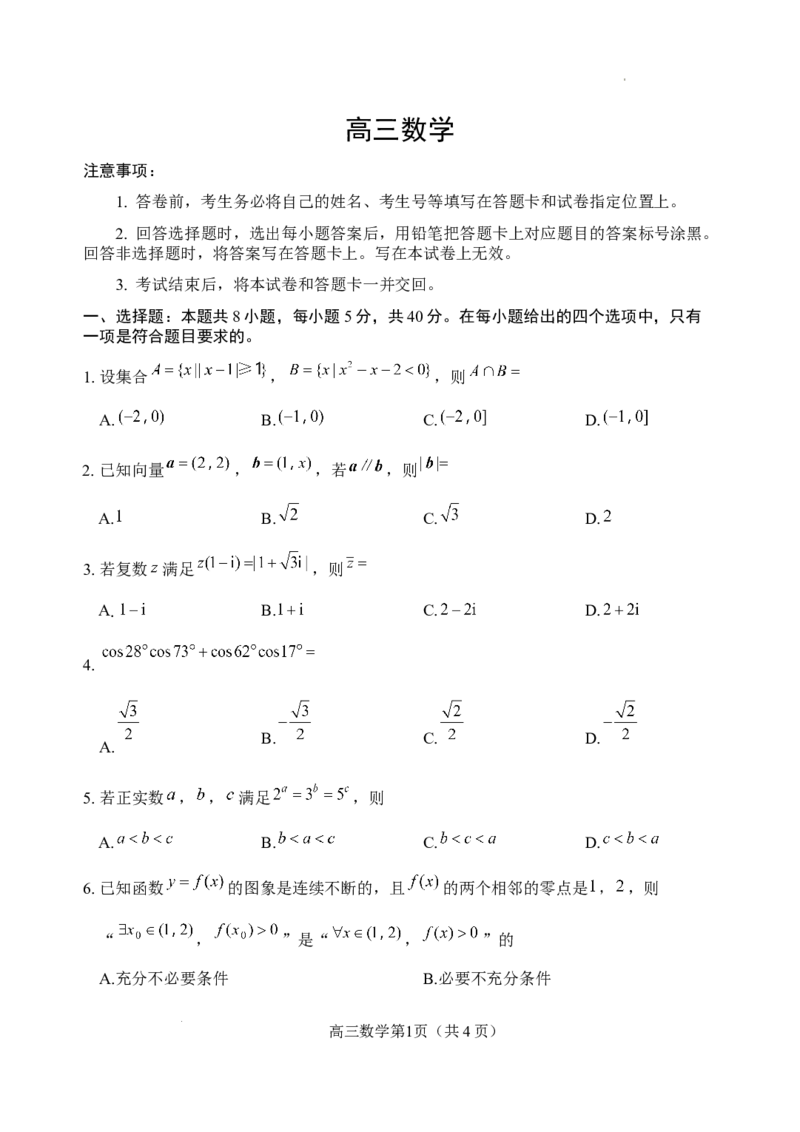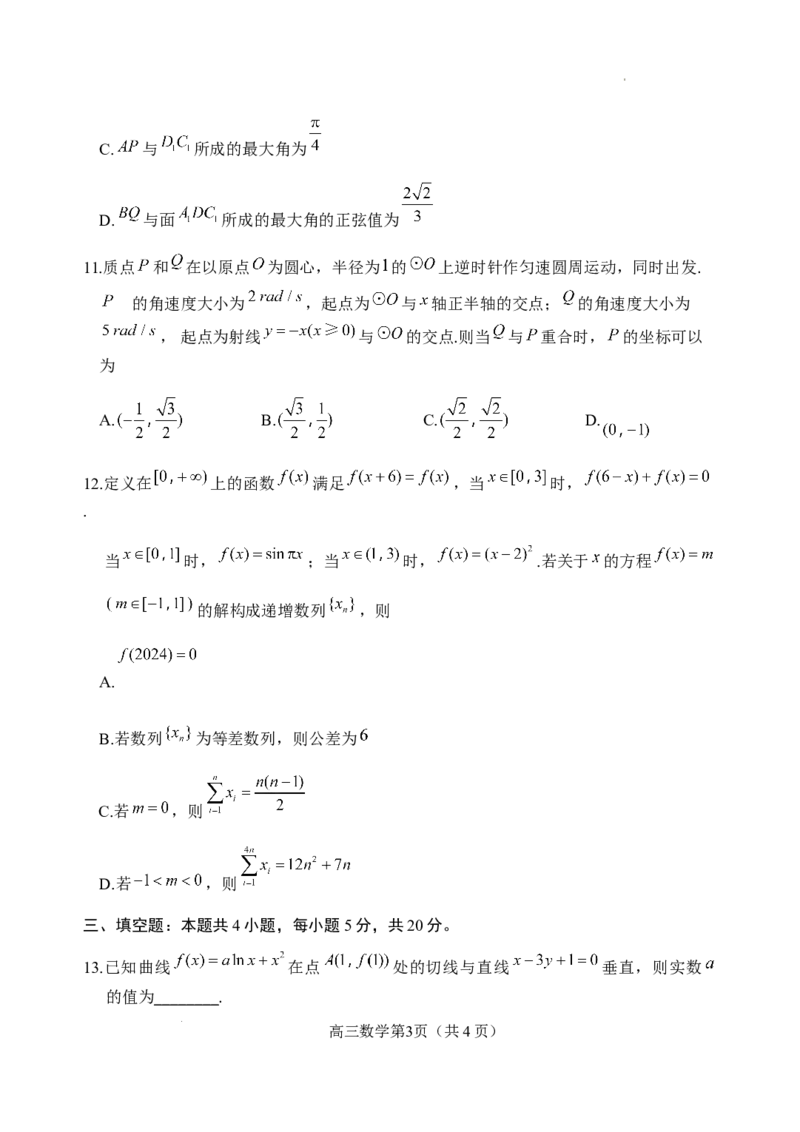文档内容
高三数学
注意事项:
1. 答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有
一项是符合题目要求的。
1.设集合 , ,则
A. B. C. D.
2. 已知向量 , ,若 ,则
A. B. C. D.
3.若复数 满足 ,则
A. B. C. D.
4.
B. C. D.
A.
5.若正实数 , , 满足 ,则
A. B. C. D.
6.已知函数 的图象是连续不断的,且 的两个相邻的零点是 , ,则
“ , ”是“ , ”的
A.充分不必要条件 B.必要不充分条件
高三数学第1页(共4页)
学科网(北京)股份有限公司C.充要条件 D.既不充分也不必要条件
7.已知 , 分别为双曲线 的左、右焦点,过点 的直线与圆
相切于点 ,且与双曲线的右支交于点 ,若 ,则该双曲线的离
心率为
A. B. C. D.
8.在四棱锥 中,底面 是边长为 的正方形, ,二面角
为 ,则该四棱锥外接球的表面积为
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符
合题目要求。全部选对得5分,部分选对得2分,有选错的得0分。
9.某学校从高一年级 名学生中抽取部分学生某次考试的数学成绩进行统计,得到如
图 所示的频率分布直
频率
方图,则 组距
0.035
A.
0.025
0.020
B.估计高一学生数学成绩的平均分落在
a
C.估计高一学生数学成绩的第三四分位数为
D.估计高一学生数学成绩在 的学生人数为 50 60 70 80 90 100 分数
10.在正方体 中, , 分别为线段 , 上的动点,则
A.存在 , 两点,使得
.
B
高三数学第2页(共4页)
学科网(北京)股份有限公司C. 与 所成的最大角为
D. 与面 所成的最大角的正弦值为
11.质点 和 在以原点 为圆心,半径为 的 上逆时针作匀速圆周运动,同时出发.
的角速度大小为 ,起点为 与 轴正半轴的交点; 的角速度大小为
,起点为射线 与 的交点.则当 与 重合时, 的坐标可以
为
A. B. C. D.
12.定义在 上的函数 满足 ,当 时,
.
当 时, ;当 时, .若关于 的方程
的解构成递增数列 ,则
A.
B.若数列 为等差数列,则公差为
C.若 ,则
D.若 ,则
三、填空题:本题共4小题,每小题5分,共20分。
13.已知曲线 在点 处的切线与直线 垂直,则实数
的值为________.
高三数学第3页(共4页)
学科网(北京)股份有限公司14. 展开式中含 项的系数为 .
15.已知函数 在 上是增函数,则 的取值范围是_______.
16.已知抛物线 的焦点为 , 是 上的动点,过点 作直线 的
垂线,垂足为 ,则 的最小值为________.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(10分)
中,角 所对的边分别为 记 的面积为 ,已知
在
.
(1)求角 的大小;
(2)若 ,求 的最大值.
18.(12分)
E F
,在多面体中,四边形 为直角梯
如图
形, 为矩形,平面 平面 , B A
H
G
, , ,
C D
, 是
的中点, 与 相交于点 .
(1)证明: 平面 ;
(2)若 ,求平面 与平面 所成角的正弦值.
高三数学第4页(共4页)
学科网(北京)股份有限公司19.(12分)
记数列 的前 项和为 ,且 , .
(1)若 为等差数列,求 ;
(2)若 ,证明: .
20.(12分)
甲、乙、丙 人做传球练习,球首先由甲传出,每个人得到球后都等可能地传给其余
人之一,设 表示经过 次传递后球传到乙手中的概率.
(1)求 , ;
(2)证明: 是等比数列,并求 ;
3)已知:若随机变量 服从两点分布,且 ,
(
则 .记前 次(即从第 次到第 次传球)中球传到乙手中的次数为 ,
求 .
21.(12分)
已知椭圆 的左、右顶点分别为 , ,右焦点 的坐标为
高三数学第5页(共4页)
学科网(北京)股份有限公司,过点 作直线交 于 , 两点(异于 , ),当 垂直于 轴时,
.
(1)求 的标准方程;
(2)直线 交直线 于点 ,证明: , , 三点共线.
22.(12分)
已知函数 .
(1)当 时,求 的单调区间;
(2)设函数 ,若 是 的极大值点,求 的值.
高三数学第6页(共4页)
学科网(北京)股份有限公司