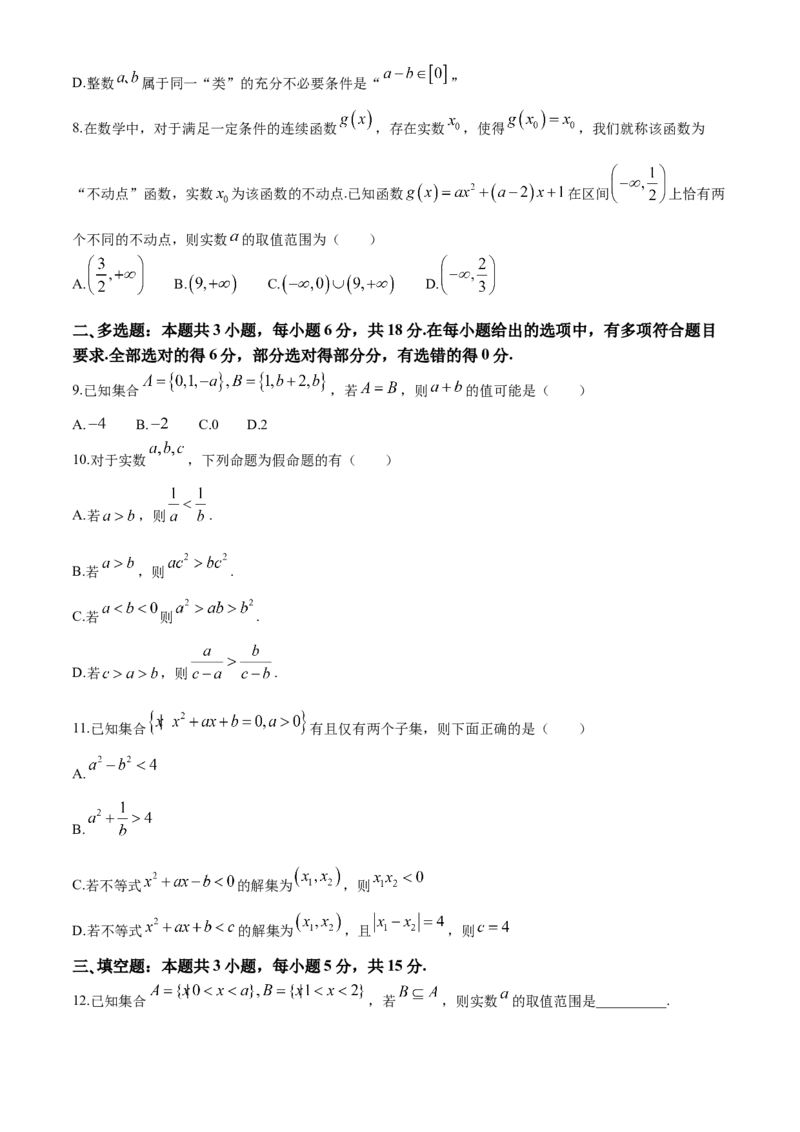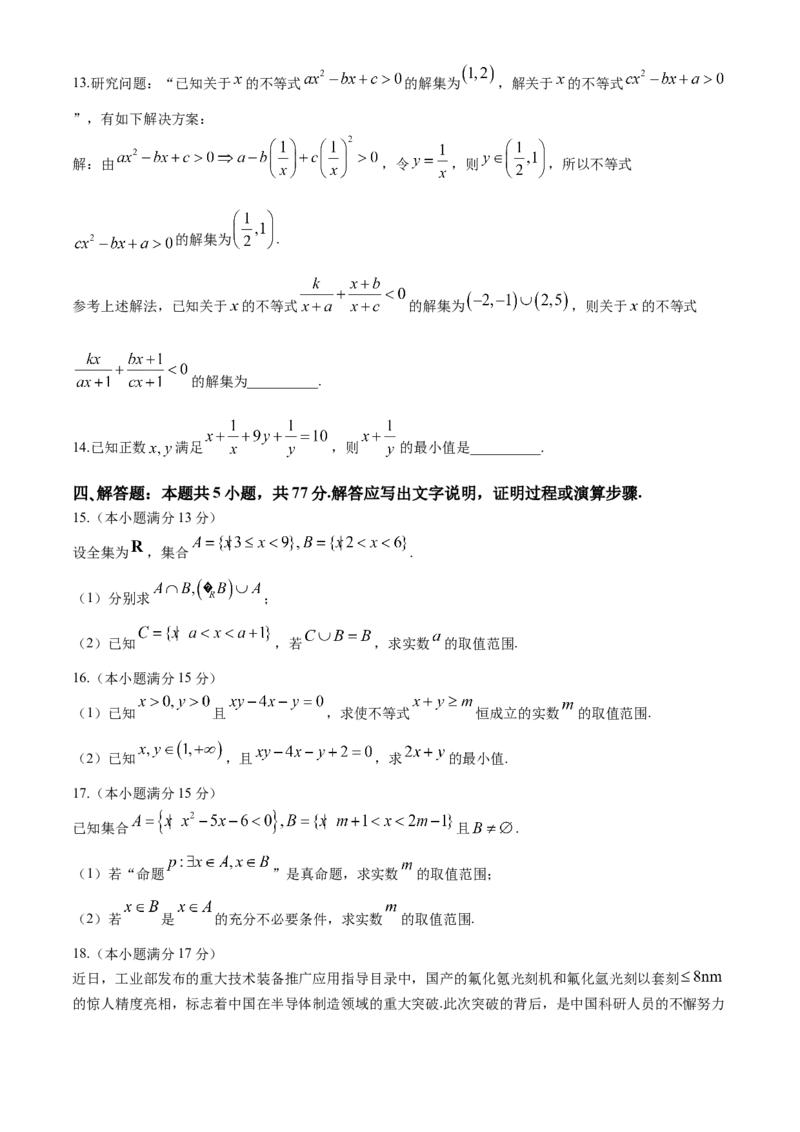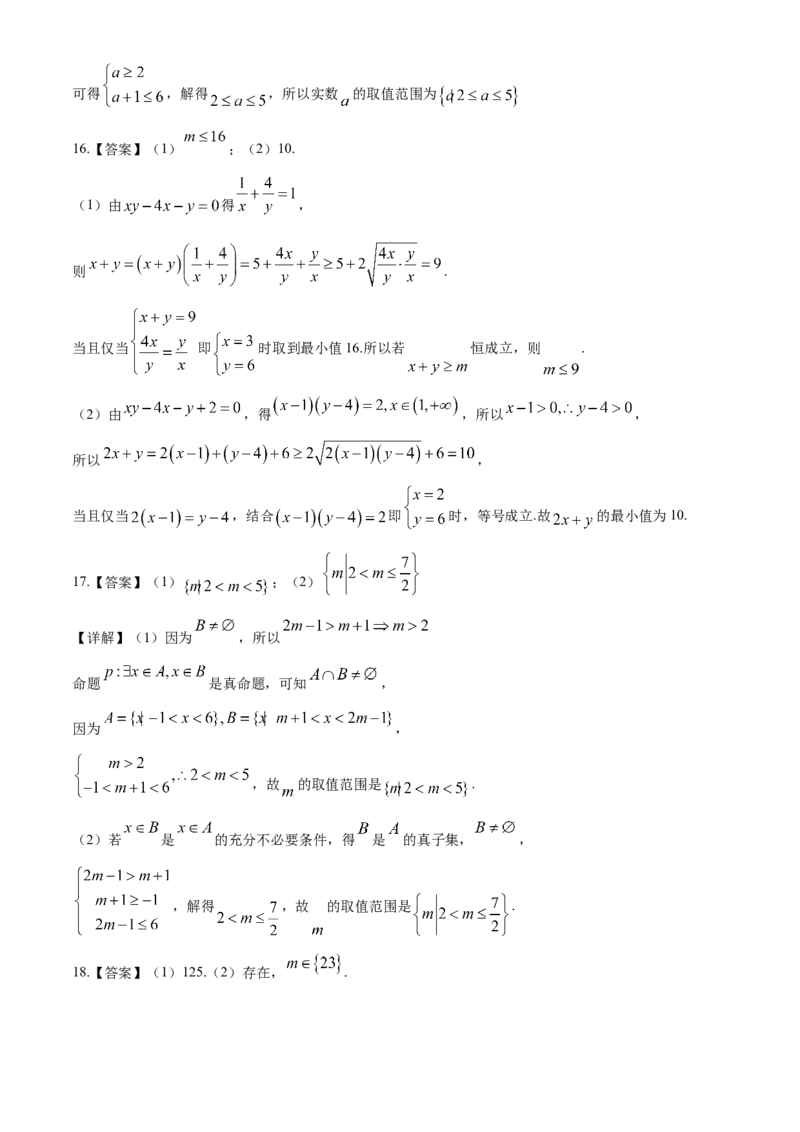文档内容
长沙市明德中学 2024 年下学期高一年级第一阶段检测
数学试卷
考试时间:120分钟考试 满分:150分 命题:高一数学备课组
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.命题“ ”的否定是( )
A. B.
C. D.
2.已知集合 ,那么 ( )
A. B. C. D.
3.函数 的零点是( )
A. B.1,2 C. D.
4.“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知集合 ,若 ,则实数 的值为( )
A.2 B. C.2或 D.4
6.对于任意实数 ,不等式 恒成立,则实数 取值范围为( )
A. B. C. D.
7.在整数集 中,被5除所得余数为 的所有整数组成一个“类”,记为 ,即
,则下面选项正确的为( )
A.
B.
C.若 ,则D.整数 属于同一“类”的充分不必要条件是“ ”
8.在数学中,对于满足一定条件的连续函数 ,存在实数 ,使得 ,我们就称该函数为
“不动点”函数,实数 为该函数的不动点.已知函数 在区间 上恰有两
个不同的不动点,则实数 的取值范围为( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对得部分分,有选错的得0分.
9.已知集合 ,若 ,则 的值可能是( )
A. B. C.0 D.2
10.对于实数 ,下列命题为假命题的有( )
A.若 ,则 .
B.若 ,则 .
C.若 则 .
D.若 ,则 .
11.已知集合 有且仅有两个子集,则下面正确的是( )
A.
B.
C.若不等式 的解集为 ,则
D.若不等式 的解集为 ,且 ,则
三、填空题:本题共3小题,每小题5分,共15分.
12.已知集合 ,若 ,则实数 的取值范围是__________.13.研究问题:“已知关于 的不等式 的解集为 ,解关于 的不等式
”,有如下解决方案:
解:由 ,令 ,则 ,所以不等式
的解集为 .
参考上述解法,已知关于 的不等式 的解集为 ,则关于 的不等式
的解集为__________.
14.已知正数 满足 ,则 的最小值是__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分13分)
设全集为 ,集合 .
(1)分别求 ;
(2)已知 ,若 ,求实数 的取值范围.
16.(本小题满分15分)
(1)已知 且 ,求使不等式 恒成立的实数 的取值范围.
(2)已知 ,且 ,求 的最小值.
17.(本小题满分15分)
已知集合 且 .
(1)若“命题 ”是真命题,求实数 的取值范围;
(2)若 是 的充分不必要条件,求实数 的取值范围.
18.(本小题满分17分)
近日,工业部发布的重大技术装备推广应用指导目录中,国产的氟化氪光刻机和氟化氩光刻以套刻
的惊人精度亮相,标志着中国在半导体制造领域的重大突破.此次突破的背后,是中国科研人员的不懈努力与自主创新.长沙某半导体企业原有400名技术人员,年人均投入 万元 ,现为加大对研发工作的
投入,该企业把原有技术人员分成技术人员和研发人员,其中技术人员 名( 且 ),
调整后研发人员的年人均投入增加 ,技术人员的年人均投入调整为 万元.
(1)若要使调整后研发人员的年总投入不低于调整前400名技术人员的年总投入,求调整后的研发人员的
人数最少为多少人?
(2)为了激励研发人员的工作热情和保持技术人员的工作积极性,企业决定在投入方面要同时满足以下
两个条件:①研发人员的年总投入始终不低于技术人员的年总投入;②技术人员的年人均投入始终不减少.
请问是否存在这样的实数 ,满足以上两个条件,若存在,求出 .范围;若不存在,说明理由.
19.(本小题满分17分)
已知集合 为非空数集,定义: .
(1)若集合 ,直接写出集合 ,
(2)若集合 ,且 ,求证: ;
(3)若集合 ,记 为集合 中元素的个数,求 的最大值.长沙市明德中学 2024 年下学期高一年级第一阶段检测
数学答案
一、
题号 1 2 3 4 5 6 7 8
答案 B C D A B D C C
题号 9 10 11
答案 BC ABD CD
三、
12. 13. 14.
四、
15.【答案】(1) 或 ;(2) .
【详解】(1)因为 ,则 ,
可得 或 ,所以 或
(2)因为 ,可知 ,且 ,可得 ,解得 ,所以实数 的取值范围为
16.【答案】(1) ;(2)10.
(1)由 得 ,
则 .
当且仅当 即 时取到最小值16.所以若 恒成立,则 .
(2)由 ,得 ,所以 ,
所以 ,
当且仅当 ,结合 即 时,等号成立.故 的最小值为10.
17.【答案】(1) ;(2)
【详解】(1)因为 ,所以
命题 是真命题,可知 ,
因为 ,
,故 的取值范围是 .
(2)若 是 的充分不必要条件,得 是 的真子集, ,
,解得 ,故 的取值范围是 .
18.【答案】(1)125.(2)存在, .【详解】(1)依题意可得调整后研发人员的年人均投入为 万元,
则 ,整理得 ,解得 ,
因为 且 ,所以 ,故 ,
所以要使这 名研发人员的年总投入不低于调整前400名技术人员的年总投入,调整后的研发人
员的人数最少为125人.
(2)由条件(1)研发人员的年总投入始终不低于技术人员的年总投入,得
,
上式两边同除以 得 ,整理得 ;
由条件(2)由技术人员年人均投入不减少,得 ,解得 ;
假设存在这样的实数 ,使得技术人员在已知范围内调整后,满足以上两个条件,
即 恒成立,
因为 ,
当且仅当 ,即 时等号成立,所以 ,
又因为 ,当 时, 取得最大值23,所以 ,
所以 ,即 ,即存在这样的 满足条件,其范围为 .
19.【答案】(1) ;(2)证明见解析;(3)1350
【详解】(1)根据定义: 所以
;
(2)由于集合 ,且 ,所以 也只有四个元素,即,所以其余的则应满足 ,所以 ,
即 ;
(3)设 ,其中 ,不妨设 ,
则 ,所以 ,
因为 ,
因为 ,所以 中最小的元素为0,最大的元素为 ,
,所以 ,
实际上当 时满足题意,
证明如下:
设 ,则 ,
,依题意有 ,解得 ,
故 的最小值为675,于是当 时, 中元素最多,
即 时满足题意,
综上所述,集合 中元素的个数的最大值为1350.