文档内容
第三章 单元质量测评
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间
120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个
选项中,只有一项是符合题目要求的)
1.函数f(x)=的定义域为( )
A.(1,+∞) B.[1,+∞)
C.[1,2) D.[1,2)∪(2,+∞)
答案 D
解析 根据题意有解得x≥1且x≠2.
2.函数f(x)=x2-4x+1,x∈[2,5]的值域是( )
A.[1,6] B.[-3,1]
C.[-3,6] D.[-3,+∞)
答案 C
解析 因为f(x)=(x-2)2-3,函数在[2,+∞)上单调递增,又f(2)=-3,
f(5)=6,所以x∈[2,5]的值域是[-3,6].
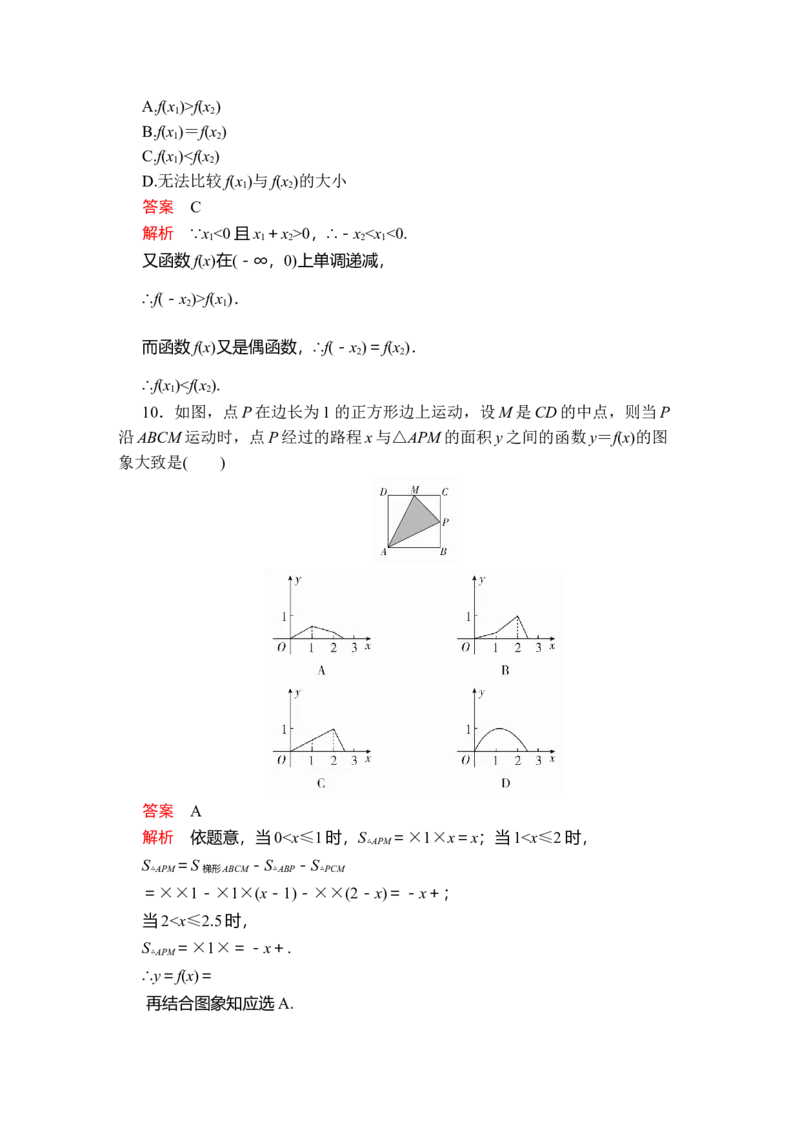
3.函数f(x)=|x-1|的图象是( )
答案 B
解析 因为f(x)=|x-1|=由分段函数的作图方法可知B正确.
4.已知A,B两地相距150 km,某人开汽车以60 km/h的速度从A地到达B地,
在B地停留1 h后再以50 km/h的速度返回A地,把汽车离开A地的距离x表示
为时间t h的函数表达式是( )
A.x=60t+50t(0≤t≤6.5)
B.x=
C.x=
D.x=
答案 D解析 由题意,得A,B两地相距150 km,某人开汽车以60 km/h的速度从A
地到达B地需2.5 h,以50 km/h的速度由B地返回A地需3 h.
所以当0≤t≤2.5时,x=60t;当2.51 D.a>3
答案 B
解析 因为函数f(x)是定义在R上的奇函数且单调递减,又由f(2-a)+f(4-
a)<0,得f(2-a)<-f(4-a)=f(a-4),所以2-a>a-4,即a<3.故选B.
9.设函数f(x)是R上的偶函数,且在(-∞,0)上单调递减.若x <0,且x +
1 1
x >0,则( )
2A.f(x )>f(x )
1 2
B.f(x )=f(x )
1 2
C.f(x )0,∴-x f(x ).
2 1
而函数f(x)又是偶函数,∴f(-x )=f(x ).
2 2
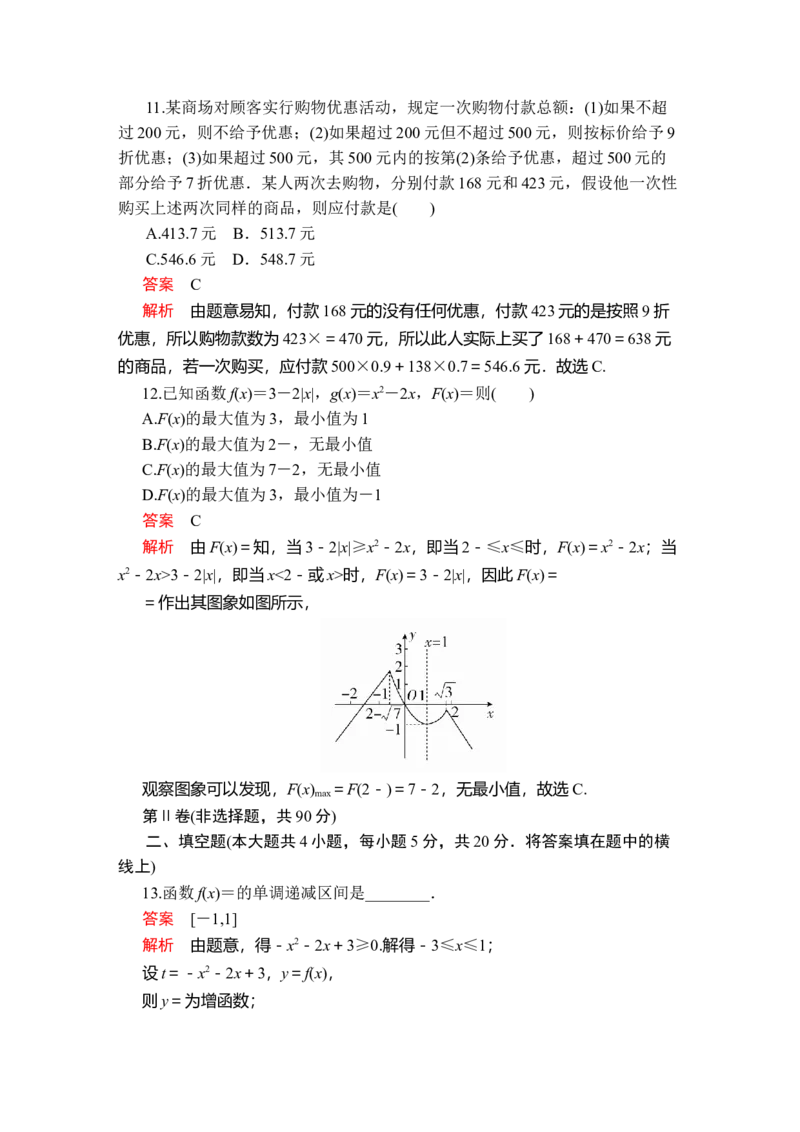
∴f(x )3-2|x|,即当x<2-或x>时,F(x)=3-2|x|,因此F(x)=
=作出其图象如图所示,
观察图象可以发现,F(x) =F(2-)=7-2,无最小值,故选C.
max
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横
线上)
13.函数f(x)=的单调递减区间是________.
答案 [-1,1]
解析 由题意,得-x2-2x+3≥0.解得-3≤x≤1;
设t=-x2-2x+3,y=f(x),
则y=为增函数;所以t=-x2-2x+3在[-3,1]上的单调递减区间,便是f(x)在[-3,1]上的单调
递减区间;
t=-x2-2x+3的对称轴为x=-1;
所以f(x)的单调递减区间为[-1,1].
14.奇函数f(x)在区间[3,10]上单调递增,在区间[3,9]上的最大值为6,最小值
为-2,则2f(-9)+f(-3)=________.
答案 -10
解析 因为函数在区间[3,10]上单调递增,所以在区间[3,9]上单调递增.
所以函数在区间[3,9]上的最小值为f(3)=-2,
最大值为f(9)=6.
又因为函数f(x)为奇函数,所以f(-3)=-f(3)=2,
f(-9)=-f(9)=-6.
所以2f(-9)+f(-3)=2×(-6)+2=-10.
15.已知函数f(x)为定义在[2-a,3]上的偶函数,在[0,3]上单调递减,并且
f>f(-m2+2m-2),则m的取值范围是________.
答案
解析 由偶函数的定义可得2-a+3=0,
则a=5,
因为m2+1>0,m2-2m+2=(m-1)2+1>0,
且f(-m2-1)=f(m2+1),f(-m2+2m-2)=f(m2-2m+2),
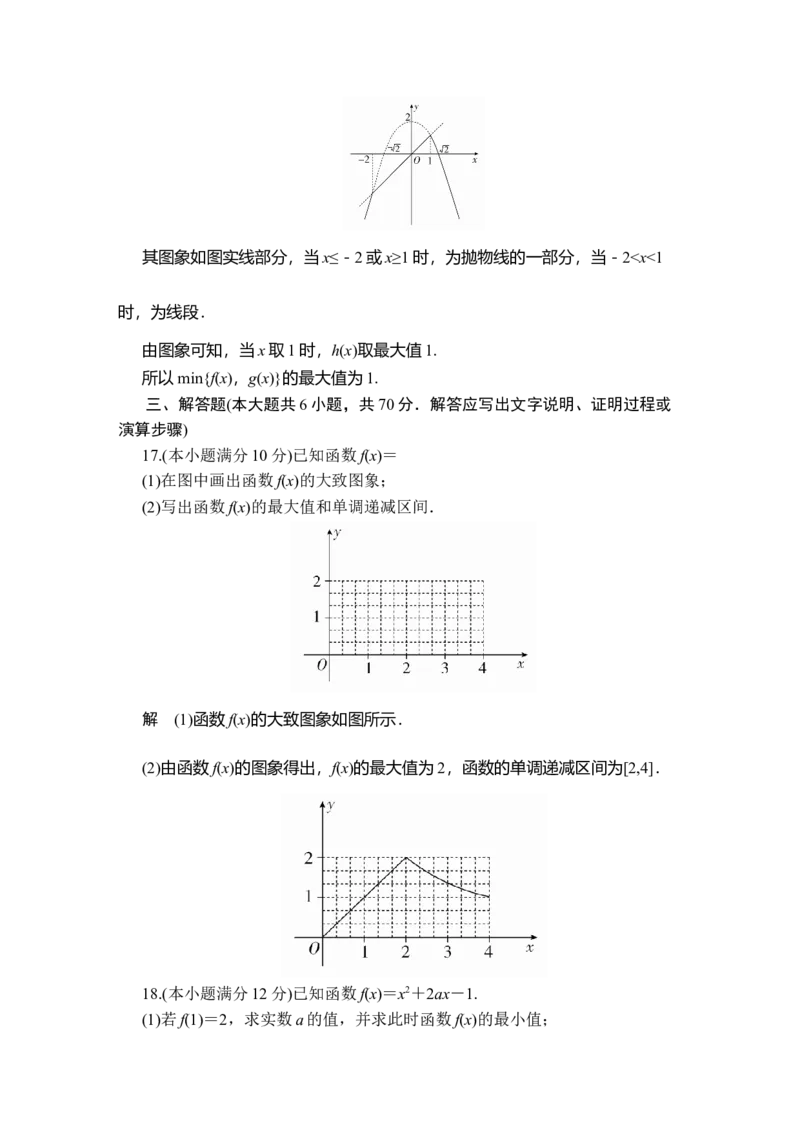
所以m2+1x,即-21,1->0.
1 2 1 2 1 2
∴f(x )-f(x )<0,即f(x )0,a>0,且f(x)为偶函数,判断F(m)+F(n)能否大于零?
并说明理由.
解 (1)因为f(-1)=0,所以a-b+1=0.①
又函数f(x)的值域为[0,+∞),所以a>0.由f(x)=a2+,知=0,
即4a-b2=0.②
联立①②,解得a=1,b=2.
所以f(x)=x2+2x+1=(x+1)2,
于是F(x)=
(2)由(1),得g(x)=f(x)-kx=x2+2x+1-kx=x2+(2-k)x+1=2+1-.
因为当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,
所以-≤-2或-≥2,即k≤-2或k≥6.
所以实数k的取值范围为(-∞,-2]∪[6,+∞).
(3)因为f(x)为偶函数,所以b=0,
所以f(x)=ax2+1,
所以F(x)=
不妨设m>n,则m>0,n<0,且|m|>|n|.
又a>0,所以F(m)+F(n)=f(m)-f(n)=(am2+1)-(an2+1)=a(m2-n2)>0,
所以F(m)+F(n)能大于零.