文档内容
班级 姓名 学号 分数
第二章 直线和圆的方程 (B 卷·能力提升练)
(时间:120分钟,满分:150分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.若点(1,1)在圆 的外部,则实数a的取值范围是( )
A. B.
C. D.
【答案】C
【解析】由题意可知 ,解得 或a>3,
则实数a的取值范围是 ,
故选:C.
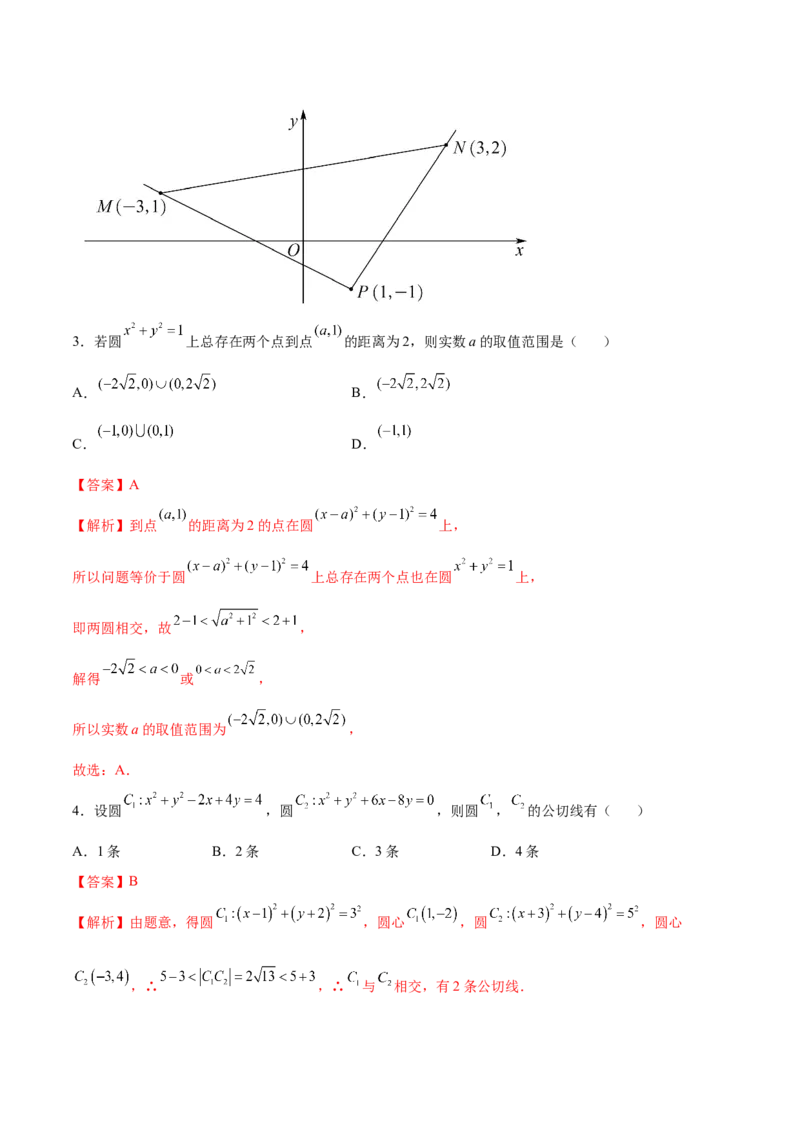
2.直线 经过点 和以 为端点的线段相交,直线 斜率的取值范围是( )
A. B. C. D.
【答案】D
【解析】 ,
画出图象如下图所示,
由图可知,直线l的斜率 满足 或
所以直线 的斜率的取值范围是 .
故选:D3.若圆 上总存在两个点到点 的距离为2,则实数a的取值范围是( )
A. B.
C. D.
【答案】A
【解析】到点 的距离为2的点在圆 上,
所以问题等价于圆 上总存在两个点也在圆 上,
即两圆相交,故 ,
解得 或 ,
所以实数a的取值范围为 ,
故选:A.
4.设圆 ,圆 ,则圆 , 的公切线有( )
A.1条 B.2条 C.3条 D.4条
【答案】B
【解析】由题意,得圆 ,圆心 ,圆 ,圆心
,∴ ,∴ 与 相交,有2条公切线.故选:B.
5.已知点 与 关于直线 对称,则a,b的值分别为( )
A.2, B.-2, C.-2, D.2,
【答案】A
【解析】易知 ,则直线 的斜率为-2,
所以 ,即 .又AB的中点坐标为 ,
代入 ,得 .
故选:A.
6.若直线 与曲线 有两个交点,则实数 的取值范围是( )
A. B.
C. D.
【答案】C
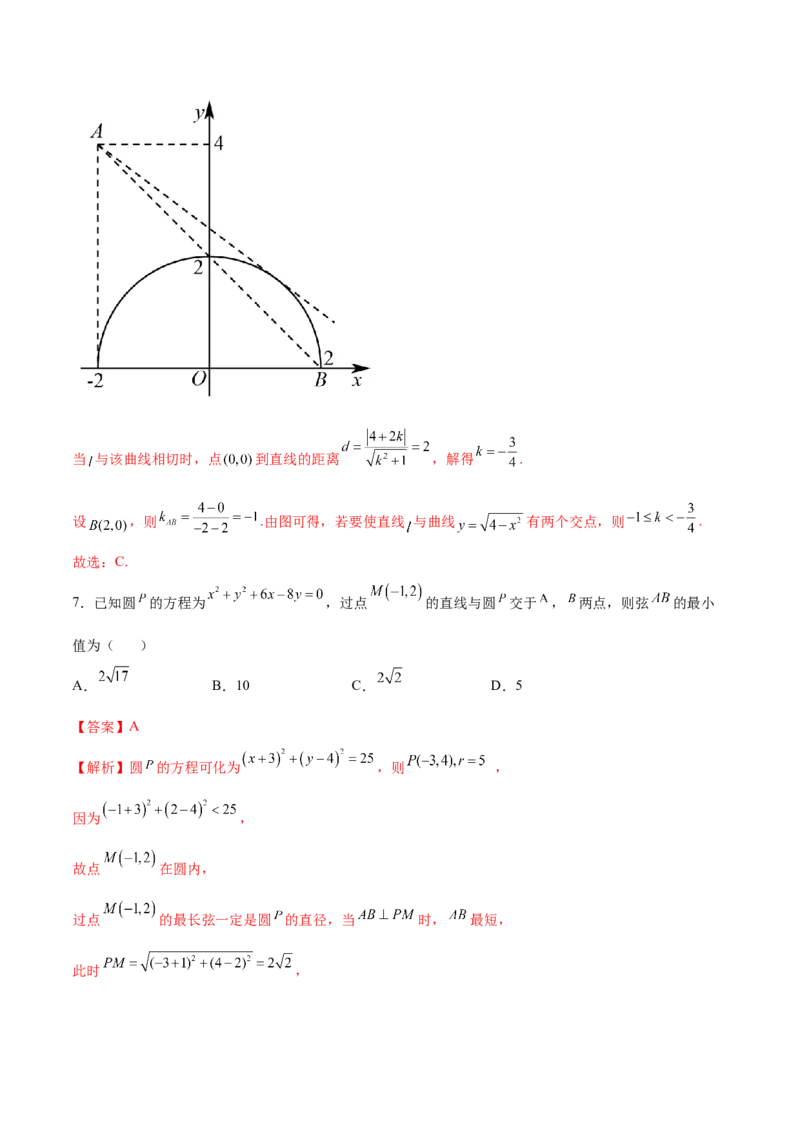
【解析】由题意,直线 的方程可化为 ,所以直线 恒过定点 , ,可
化为 其表示以 为圆心,半径为2的圆的一部分,如图.当 与该曲线相切时,点 到直线的距离 ,解得 .
设 ,则 .由图可得,若要使直线 与曲线 有两个交点,则 .
故选:C.
7.已知圆 的方程为 ,过点 的直线与圆 交于 , 两点,则弦 的最小
值为( )
A. B.10 C. D.5
【答案】A
【解析】圆 的方程可化为 ,则 ,
因为 ,
故点 在圆内,
过点 的最长弦一定是圆 的直径,当 时, 最短,
此时 ,则 ,
故选:A.
8.若圆 )与圆 交于A、B两点,则
tan∠ANB的最大值为( )
A. B. C. D.
【答案】D
【解析】 可化为 ,
故圆N的圆心为 ,半径为 ,
由题意可知:AB为圆M与圆N的公共弦,且圆M的半径为1,
所以 且 ,故 ,
当 的坐标为 时, ,
在△NAB中, ,
又 , 在 上单调递减,
故 为锐角,且当 时, 最大,又 在 上单调递增,
所以当 最大时, 取得最大值,且最大值为 ,
故选:D
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得5分,部分选对的得2分,有选错的得0分。
9.已知两圆的方程分别为 , ,则下列说法正确的是( )
A.若两圆内切,则r=9
B.若两圆的公共弦所在直线的方程为8x-6y-37=0,则r=2
C.若两圆在交点处的切线互相垂直,则r=3
D.若两圆有三条公切线,则r=2
【答案】ABC
【解析】圆 的圆心为(0,0),半径为4,圆 的圆心为(4,-3),半径
为r,两圆的圆心距 .
对于A,若两圆内切,则 ,则r=9,故A正确;
对于B,联立两圆的方程可得 ,令 ,得r=2,故B正确;对于C,若两圆
在交点处的切线互相垂直,则一个圆的切线必过另一个圆的圆心,
(圆的切线与经过切点的半径垂直,又∵两圆切线相互垂直且交于一公共切点,所以两切线分别与另一圆
的半径重合,半径经过圆心,所以此时两切线经过圆心)
分别设两圆的圆心为 ,则
如图,所以 ,解得r=3,故C正确;对于D,若两圆有三条公切线,则两圆外切,则 ,得r=1,故D错误.
故选:ABC
10.(多选)已知直线 与直线 ,则直线 与直线 的位置关系可能是
( )
A.相交 B.重合 C.平行 D.垂直
【答案】ABC
【解析】直线 的斜率为 ,过定点 ,
直线 的斜率为 ,过点 .
若直线 与 相交,则 ,而 ,
即 可以成立,A正确;
若直线 与 重合,则 ,且 ,而 ,
可以有 ,B正确;
若直线 与 平行,则 且 ,而 ,
可以有 ,C正确;
若直线 与 垂直,则 ,则 ,
与 矛盾,直线 与 不可能垂直,D错误.
故选:ABC.11.在平面直角坐标系xOy中,已知直线 与x轴交于点A,与y轴交于点B,圆
,则( )
A.若c=0,则点O在圆C上
B.直线l与坐标轴围成的三角形的面积为
C.若点O在圆C内部,则c的取值范围为(0,+∞)
D.若 ,则圆C与 OAB中与 平行的中位线相切
【答案】ACD
【解析】对于 ,圆 ,令 ,恰符合;
对于B,由已知 , ,三角形面积为 ;
对于C,点O在圆C内部,则 ,即 ;
对于D,圆 ,
, , 中点为 , 中点为 ,
与 平行的中位线方程为 ,即 ,
圆心到此中位线的距离为 ,
此条中位线与圆 相切.
故选:ACD.
12.在平面直角坐标系 中, ,点 满足 ,设点 的轨迹为 ,则( )
A. 的周长为B. ( 不重合时)平分
C. 面积的最大值为6
D.当 时,直线 与轨迹 相切
【答案】ABD
【解析】设 ,因为 ,且点 满足 ,可得 ,整理得
,即曲线 的方程为 .
对于A中,曲线 为半径为 的圆,所以周长为 ,所以A正确;
对于B中,因为 ,所以 ,所以 ,
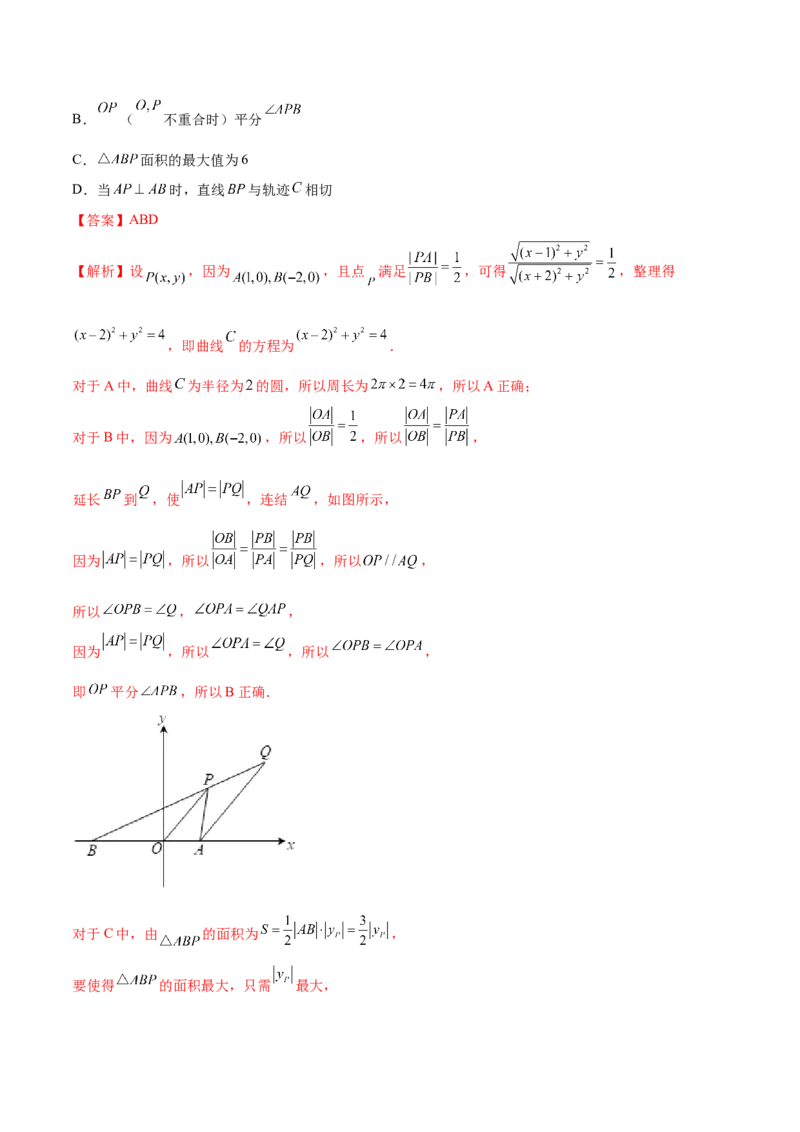
延长 到 ,使 ,连结 ,如图所示,
因为 ,所以 ,所以 ,
所以 , ,
因为 ,所以 ,所以 ,
即 平分 ,所以B正确.
对于C中,由 的面积为 ,
要使得 的面积最大,只需 最大,由由点 的轨迹为 ,可得 ,
所以 面积的最大值为 ,所以C错误;
对于D中,当 时, 或 ,
不妨取 ,则直线 ,即 ,
因为圆心 到直线 的距离为 ,
所以 ,即直线 与圆相切,所以D正确.
故选:ABD.
三、填空题:本题共4小题,每小题5分,共20分。
13.已知圆 .若圆 与圆 有三条公切线,则 的值为
___________.
【答案】
【解析】由 ,得 ,
所以圆 的圆心为 ,半径为 ,
因为圆 ,所以圆 的圆心为 ,半径为 ,
因为圆 与圆 有三条公切线,所以圆 与圆 相外切,即 ,解得 ,
所以 的值为 .
故答案为: .
14.过点 作圆 的两条切线,切点分别为 、 ,则直线 的方程为_______.
【答案】
【解析】方法1:由题知,圆 的圆心为 ,半径为 ,
所以过点 作圆 的两条切线,切点分别为 、 ,
所以 ,
所以直线 的方程为 ,即 ;
方法2:设 , ,则由 ,可得 ,
同理可得 ,
所以直线 的方程为 .
故答案为:
15.过点 且斜率为 的直线l与x,y轴分别交于点P,Q,过点P,Q作直线 的垂
线,垂足分别为R,S,则四边形PRSQ面积的最小值为________.
【答案】
【解析】由已知得直线 l的方程为 ,则 , ,
由此可得直线PR和QS的方程分别为 和 ,
点 到直线 的距离为 ,同理 ,直线 和直线 的距离为 ,
故
,
当且仅当 ,即 时等号成立.
故答案为: .
16.已知点 分别在直线 : 与直线 : 上,且 ,点 ,
则 的最小值为____.
【答案】
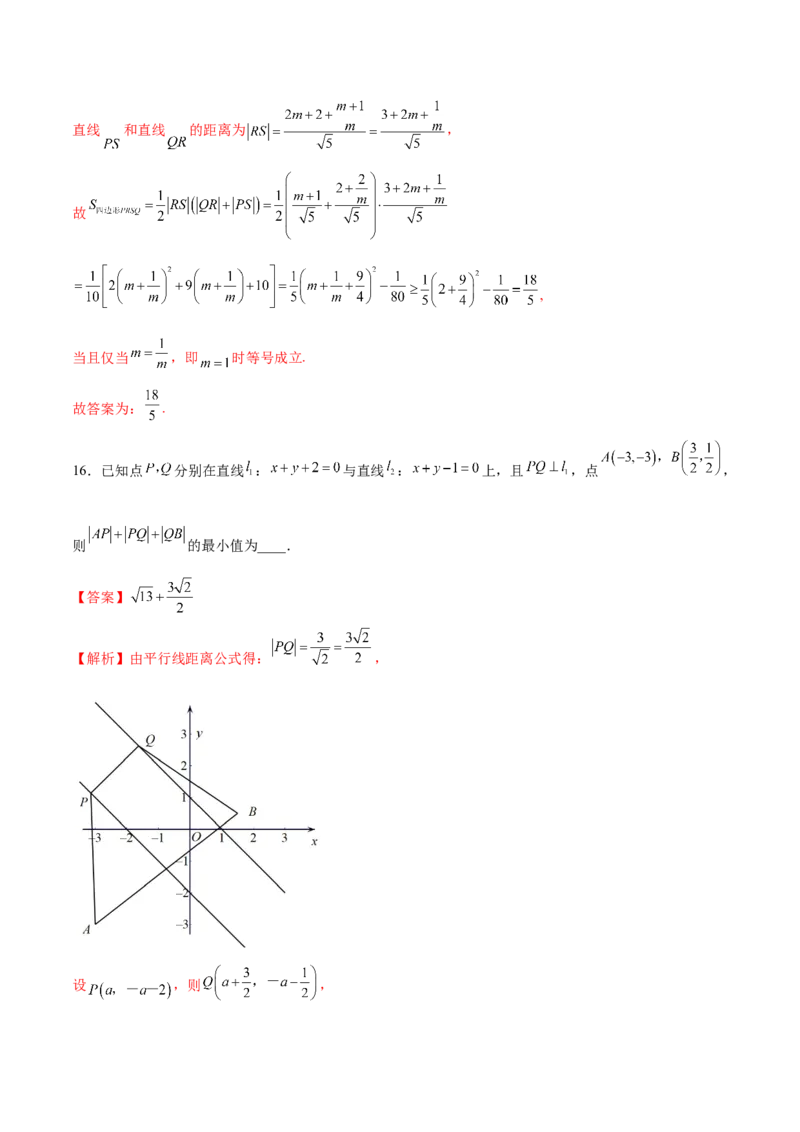
【解析】由平行线距离公式得: ,
设 ,则 ,所以
,
设点 ,如下图:
则有:
即当 三点共线时等号成立),
综上, .
故答案为:
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步棸。
17.(10分)
已知圆过点 , .
(1)求圆心所在直线的方程;
(2)求周长最小的圆的标准方程;
(3)求圆心在直线2x-y-4=0上的圆的标准方程;
(4)若圆心的纵坐标为2,求圆的标准方程.
【解析】(1)由题意可知线段AB的中点坐标是 ,
∵直线AB的斜率 ,且圆心在线段AB的垂直平分线上,
∴圆心所在直线的方程为 ,即x-3y+3=0.
(2)当线段AB为圆的直径时,过点A,B的圆的半径最小,从而周长最小,即圆心为线段AB的中点(0,1),半径为 .
则所求圆的标准方程为 .
(3)由(1)可知,圆心所在直线的方程为 ,
又∵圆心也在直线2x-y-4=0上,∴圆心是这两条直线的交点,
∴ ,解得 ,即圆心的坐标是(3,2),
∴半径 ,
∴所求圆的标准方程是 .
(4)设圆心的坐标为(m,2),
由(1)知m-3×2+3=0,得m=3,
∴圆的半径 ,
∴所求圆的标准方程为 .
18.(12分)
已知圆 : ,直线 : ,点 .
(1)判断直线 与圆 的位置关系;
(2)设直线 与圆 交于不同的两点 ,求弦 的中点 的轨迹方程;
(3)在(2)的条件下,若 ,求直线 的方程.
【解析】(1)因为直线 : 过定点 ,
又 ,所以 在圆 内,
所以直线 与圆 相交;
(2)设 ,当 与 不重合,即 时,连接 , ,则 ,根据勾股定理.则 ,化简得: ( );当
与 重合时, , 也满足上式,故弦 的中点的轨迹方程为 ;
(3)设 , ,因为 ,所以 ,
所以 ,化简得 . ①
又 消去 并整理得 ,
所以 ②, . ③
由①②③联立,解得 ,
所以直线 的方程为 或 .
19.(12分)
已知直线 和点 , .
(1)在直线l上求一点P,使 的值最小;
(2)在直线l上求一点P,使 的值最大.
【解析】(1)设A关于直线l的对称点为 ,则 ,
解得 ,故 ,
又∵P为直线l上的一点,则 ,
当且仅当B,P, 三点共线时等号成立,此时 取得最小值 ,
点P即是直线 与直线l的交点.
由 ,解得 ,故所求的点P的坐标为 .
(2)由题意,知A,B两点在直线l的同侧,P是直线l上的一点,
则 ,当且仅当A,B,P三点共线时等号成立,
此时 取得最大值 ,点P即是直线AB与直线l的交点,
又∵直线AB的方程为 ,
∴由 ,解得 ,
故所求的点P的坐标为 .
20.(12分)
在平面直角坐标系中,O为坐标原点,过点 作直线l分别与x轴正半轴、y轴正半轴交于点A,B.
(1)求 面积的最小值及此时直线l的方程;
(2)求当 取得最小值时直线l的方程.
【解析】(1)∵点 在第一象限,且直线l分别与x轴正半轴 、y轴正半轴相交,
∴直线l的斜率 ,
则设直线l的方程为 , ,
令 ,得 ;令 ,得 .
∴ .
∵ ,∴ ,
∴ ,当且仅当 ,即 时等号
成立.
∴ 面积的最小值为6.此时直线l的方程为 ,即 .
(2)设 , , , .
∵A,P,B三点共线,∴ ,整理得 ,
∴ ,当且仅当
,即 时等号成立,
∴当 取得最小值时,直线l的方程为 ,即 .
21.(12分)
已知圆C经过点 , 及(3,0).过坐标原点O,且斜率为k的直线l与圆C交于M,N两点.
(1)求圆C的标准方程;
(2)若点 ,分别记直线PM,直线PN的斜率为 , ,证明: 为定值.
【解析】(1)设圆C的方程为 ,
∴ ,解得 ,
∴圆C的方程为 ,其标准方程为 .
(2)设 , .由题意得直线l的方程为 ,
由 ,得 ,
∴ ,
∴ ,∴ ,
.
即 为定值0.
22.(12分)
已知圆C的圆心位于x轴的正半轴上,该圆与直线 相切,且被y轴截得的弦长为 ,圆C
的面积小于13.
(1)求圆C的标准方程.
(2)设过点M(0,3)的直线l与圆C交于不同的两点A,B,以OA,OB为邻边作平行四边形OADB.是否
存在这样的直线l,使得直线OD与MC恰好平行?如果存在,求出l的方程;如果不存在,请说明理由.
【解析】(1)设圆C的方程为 ,
由题意,知 ,解得 或 ,
又圆C的面积 ,∴ , ,
∴圆C的标准方程为 .
(2)当直线l的斜率不存在时,直线l的方程为x=0,不满足题意.
当直线l的斜率存在时,假设存在满足题意的直线l,设直线l的方程为 , , ,
由 ,得 ,
∵直线l与圆C相交于不同的两点,
∴ ,解得 或 .
, ,
∵线段OD过线段AB的中点 ,且线段AB与OD互相平分,
∴点D的坐标为 ,即 ,
又MC的斜率为 ,∴ ,解得 .
由于 ,故不存在这样的直线l.