文档内容
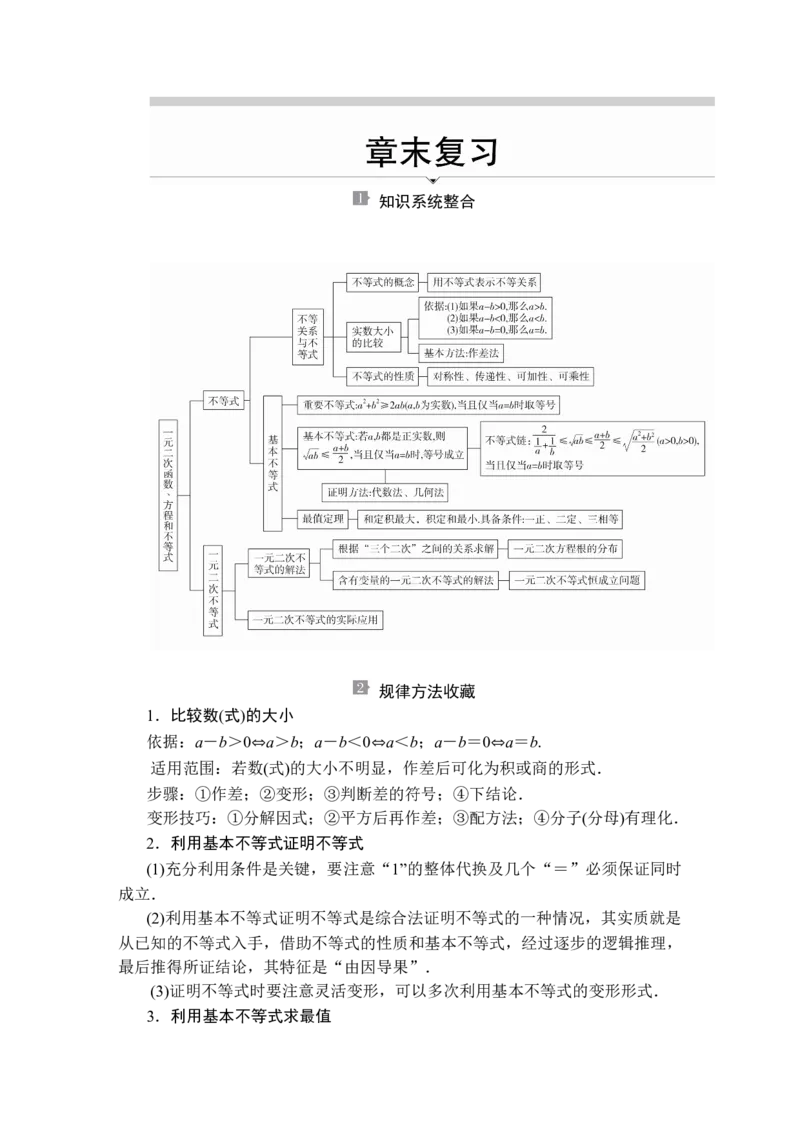
知识系统整合
规律方法收藏
1.比较数(式)的大小
依据:a-b>0⇔a>b;a-b<0⇔a<b;a-b=0⇔a=b.
适用范围:若数(式)的大小不明显,作差后可化为积或商的形式.
步骤:①作差;②变形;③判断差的符号;④下结论.
变形技巧:①分解因式;②平方后再作差;③配方法;④分子(分母)有理化.
2.利用基本不等式证明不等式
(1)充分利用条件是关键,要注意“1”的整体代换及几个“=”必须保证同时
成立.
(2)利用基本不等式证明不等式是综合法证明不等式的一种情况,其实质就是
从已知的不等式入手,借助不等式的性质和基本不等式,经过逐步的逻辑推理,
最后推得所证结论,其特征是“由因导果”.
(3)证明不等式时要注意灵活变形,可以多次利用基本不等式的变形形式.
3.利用基本不等式求最值(1)利用基本不等式求最值,必须同时满足以下三个条件:一正、二定、三
相等.
即:①x,y都是正数.
②积xy(或和x+y)为常数(有时需通过“配凑、分拆”凑出定值).
③x与y必须能够相等(等号能够取到).
(2)构造定值条件的常用技巧
①加项变换;②拆项变换;③统一换元;④平方后利用基本不等式.
4.解一元二次不等式的步骤
当a>0时,解形如ax2+bx+c>0(≥0)或ax2+bx+c<0(≤0)的一元二次不
等式的一般步骤如下:
(1)确定对应方程ax2+bx+c=0的解;
(2)画出对应函数y=ax2+bx+c的图象的简图;
(3)由图象写出不等式的解集.
特别提醒:(1)在通过图象获取解集时,注意不等式中的不等号方向、是否为
严格不等关系及Δ=0时的特殊情况.
(2)当a<0时,解不等式可以从两个方面入手:①画出对应图象进行直接判
定(此时图象开口向下);②两边同乘以-1,把a转变为-a再进行求解.
5.一元二次不等式的实际应用
不等式在解决生活、生产中的一些实际问题中有着广泛的应用,主要有范围
问题、最值问题等.解一元二次不等式的应用问题的关键在于构造一元二次不等
式模型.解题的一般步骤是:
(1)理清题意:弄清问题的实际背景和意义,用数学语言来描述问题.
(2)简化假设:精选问题中的关键变量.
(3)列出关系式:建立变量间的不等关系式.
(4)求解:运用数学知识解相应不等式.
(5)检验并作答:将所得不等式的解集放回原题中检验是否符合实际情况,
然后给出问题的答案.
学科思想培优
一、常数代换法
[典例1] 已知正数x,y满足x+y=1,则+的最小值为( )
A.5 B. C. D.2
解析 因为x+y=1,所以x+(1+y)=2,则2=[x+(1+y)]=++5≥2+5=
9,所以+≥,当且仅当即时,等号成立,因此+的最小值为.故选C.
答案 C
二、消元法
[典例2] 设x,y,z为正实数,满足x-2y+3z=0,则的最小值为________.
解析 解法一:由x-2y+3z=0,得y=,故==≥=3,当且仅当x=y=3z时取等号,即的最小值为3.
解法二:由x-2y+3z=0,得x=2y-3z,=2->0.
==≥=3.当且仅当x=y=3z时取等号,即的最小值为3.
答案 3
三、配凑法
1.从和或积为定值的角度入手配凑
某些不等式的约束条件可看成若干变元的和或积的定值,在不等式的变形中,
配凑出这些定值,可使问题巧妙获解.常见的配凑变形有化积为和、常数的代换、
加法结合律等常规运算和技巧.
[典例3] 设x>0,y>0,x2+=1,求x的最大值.
解 ∵x>0,y>0,x2与的和为定值,
∴x==≤·=·=,当且仅当x2=,即x=,y=时取等号,即x的最大值为.
[典例4] 已知x,y,z为正数,且满足xyz(x+y+z)=1,求(x+y)(y+z)的最
小值.
解 由条件得x+y+z=,则(x+y)(y+z)=xy+xz+y2+yz=y(x+y+z)+xz=
y·+xz=+xz≥2,当且仅当=xz,即xz=1时取等号,故(x+y)(y+z)的最小值为
2.
[典例5] 设a ,a ,a ,…,a 均为正实数,求证:++…++≥a +a +a
1 2 3 n 1 2 3
+…+a .
n
证明 为了约去中的分母,可考虑配上一项 a ,于是有+a ≥2a ,+
k+1 2 1
a ≥2a ,…,+a ≥2a ,+a ≥2a ,当且仅当a =a =…=a 时取等号.以上
3 2 n n-1 1 n 1 2 n
不等式相加,化简,可得原不等式成立.
2.从取等号的条件入手配凑
在题中约束条件下,各变元将取某个特定值,这就提示我们可考虑用这些值
来进行配凑.
[典例6] 设a,b,c>0,a+b+c=1,求++的最大值.
解 ·≤=,·≤,·≤.
以上三式相加,并利用a+b+c=1,得(++)≤6,故++的最大值为3.
四、判别式法在“三个二次”问题中的应用
一元二次方程、一元二次不等式与二次函数的关系十分密切,习惯上称为
“三个二次”问题.根据判别式法在解一元二次方程中的作用,可见判别式法在
“三个二次”问题中的重要性.
1.求变量的取值范围
[典例7] 不等式(m2-2m-3)x2-(m-3)x-1<0对任意x∈R恒成立,求实数
m的取值范围.
解 (m2-2m-3)x2-(m-3)x-1<0对任意x∈R恒成立.①若m2-2m-3=0,则m=-1或m=3.
当m=-1时,不符合题意;当m=3时,符合题意.
②若m2-2m-3≠0,设y=(m2-2m-3)x2-(m-3)x-1<0对任意x∈R恒成
立.
则m2-2m-3<0,Δ=b2-4ac=5m2-14m-3<0,
解得-0恒成立.
证明 不等式可变形为y2+2xy+2x2-4x+5>0,将不等式左边看作关于 y的
二次函数,令z=y2+2xy+2x2-4x+5,则关于y的一元二次方程y2+2xy+2x2-
4x+5=0的根的判别式Δ=4x2-4(2x2-4x+5)=-4(x-2)2-4<0,即Δ<0.则对
于二次函数z=y2+2xy+2x2-4x+5,其图象开口向上,且在x轴上方,所以z>0
恒成立,即2x2+2xy+y2-4x+5>0恒成立.
五、含变量的不等式恒成立问题
[典例10] 对于满足0≤p≤4的一切实数,不等式x2+px>4x+p-3恒成立,
试求x的取值范围.
解 原不等式可化为x2+px-4x-p+3>0,
令y=x2+px-4x-p+3
=(x-1)p+(x2-4x+3).
由题设得
解得x>3或x<-1.故x的取值范围是x<-1或x>3.