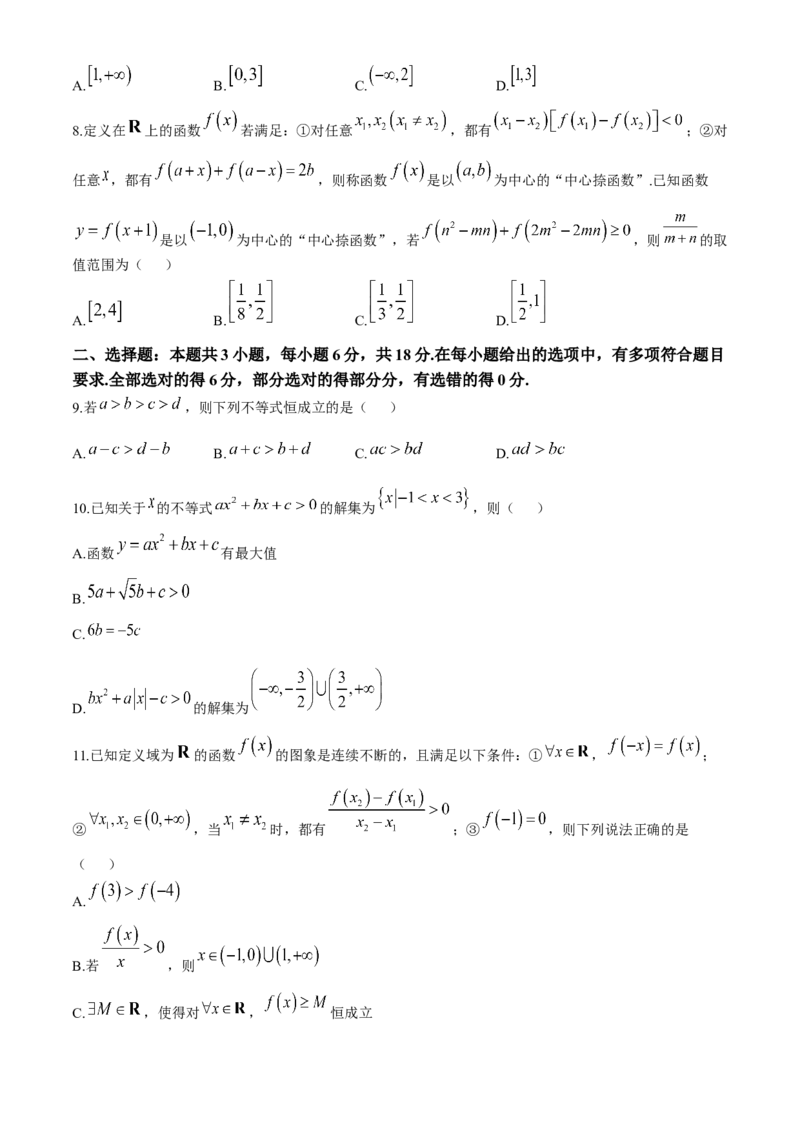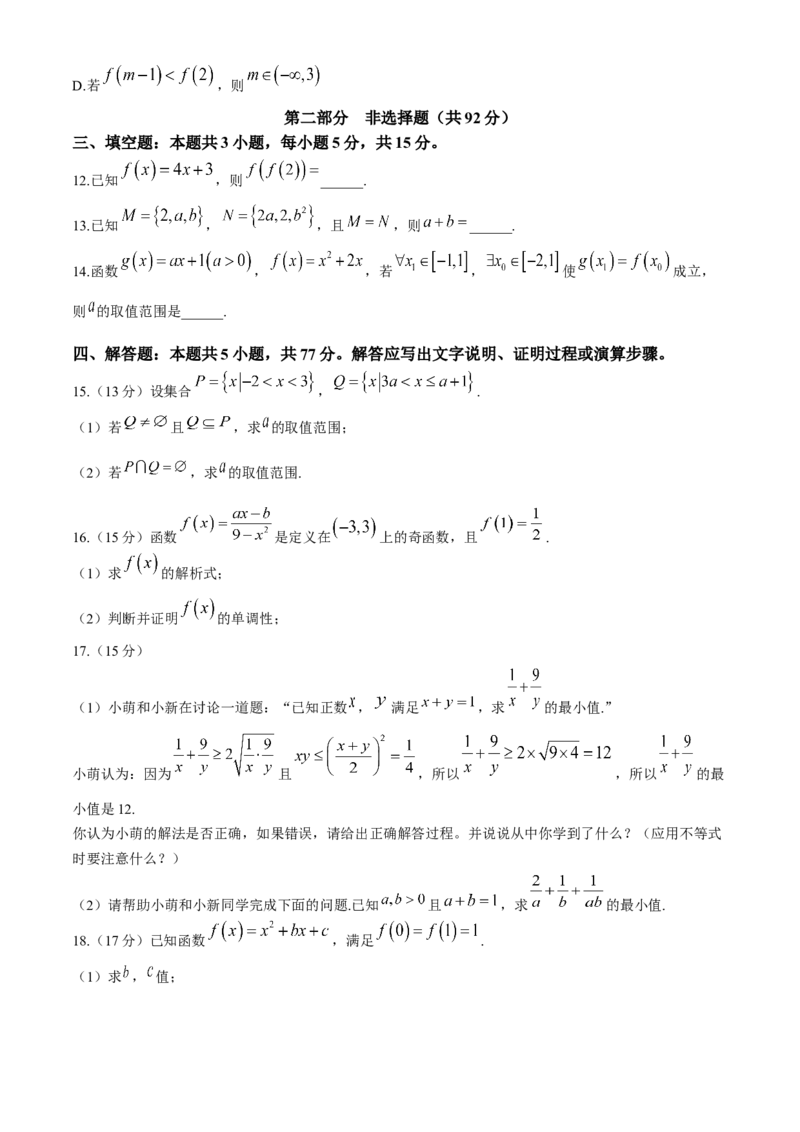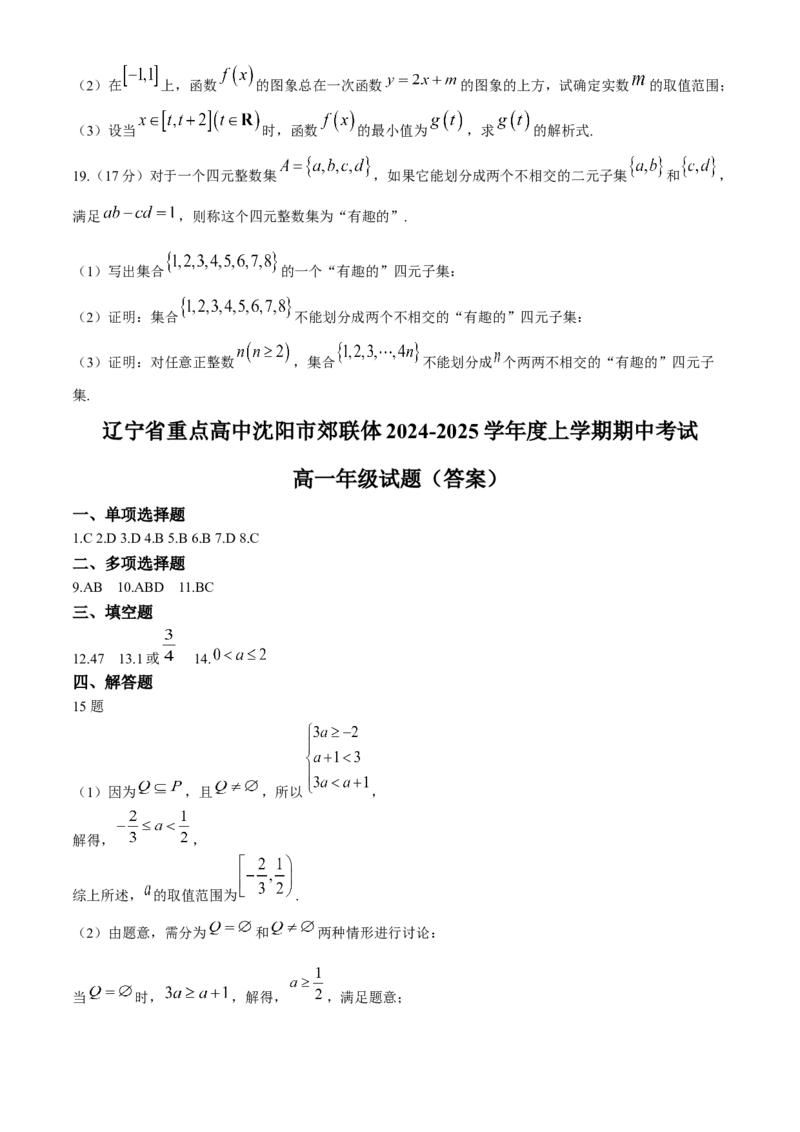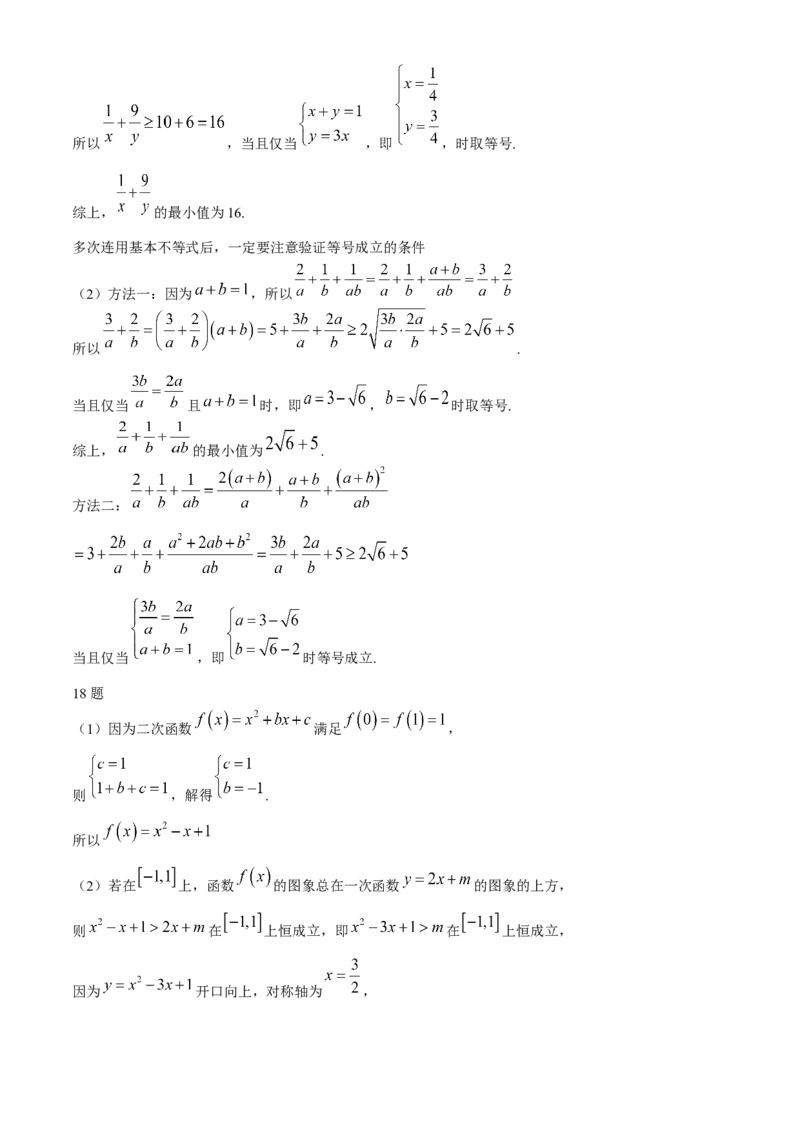文档内容
辽宁省重点高中沈阳市郊联体
2024-2025 学年度上学期期中考试高一年级试题
数学
第一部分 选择题(共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.已知集合 ,集合 , ,则 ( )
A、 B. C. D.
2.不等式 的解集是( )
A. B. C. D.
3.函数 的定义域为 ,函数 ,则 的定义域为( )
A. B. C. D.
4.使“ ”成立的一个充分不必要条件是( )
A. B. C. D.
5.命题 : , ,则命题 的否定是( )
A. , B. ,
C. , D. ,
6.已知函数 为 上的增函数,则实数 的取值范围是( )
A. B. C. D.
7.已知函数 在闭区间 上有最大值6,最小值2,则 的取值范围是( )A. B. C. D.
8.定义在 上的函数 若满足:①对任意 ,都有 ;②对
任意 ,都有 ,则称函数 是以 为中心的“中心捺函数”.已知函数
是以 为中心的“中心捺函数”,若 ,则 的取
值范围为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若 ,则下列不等式恒成立的是( )
A. B. C. D.
10.已知关于 的不等式 的解集为 ,则( )
A.函数 有最大值
B.
C.
D. 的解集为
11.已知定义域为 的函数 的图象是连续不断的,且满足以下条件:① , ;
② ,当 时,都有 ;③ ,则下列说法正确的是
( )
A.
B.若 ,则
C. ,使得对 , 恒成立D.若 ,则
第二部分 非选择题(共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12.已知 ,则 ______.
13.已知 , ,且 ,则 ______.
14.函数 , ,若 , 使 成立,
则 的取值范围是______.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)设集合 , .
(1)若 且 ,求 的取值范围;
(2)若 ,求 的取值范围.
16.(15分)函数 是定义在 上的奇函数,且 .
(1)求 的解析式;
(2)判断并证明 的单调性;
17.(15分)
(1)小萌和小新在讨论一道题:“已知正数 , 满足 ,求 的最小值.”
小萌认为:因为 且 ,所以 ,所以 的最
小值是12.
你认为小萌的解法是否正确,如果错误,请给出正确解答过程。并说说从中你学到了什么?(应用不等式
时要注意什么?)
(2)请帮助小萌和小新同学完成下面的问题.已知 且 ,求 的最小值.
18.(17分)已知函数 ,满足 .
(1)求 , 值;(2)在 上,函数 的图象总在一次函数 的图象的上方,试确定实数 的取值范围;
(3)设当 时,函数 的最小值为 ,求 的解析式.
19.(17分)对于一个四元整数集 ,如果它能划分成两个不相交的二元子集 和 ,
满足 ,则称这个四元整数集为“有趣的”.
(1)写出集合 的一个“有趣的”四元子集:
(2)证明:集合 不能划分成两个不相交的“有趣的”四元子集:
(3)证明:对任意正整数 ,集合 不能划分成 个两两不相交的“有趣的”四元子
集.
辽宁省重点高中沈阳市郊联体 2024-2025 学年度上学期期中考试
高一年级试题(答案)
一、单项选择题
1.C 2.D 3.D 4.B 5.B 6.B 7.D 8.C
二、多项选择题
9.AB 10.ABD 11.BC
三、填空题
12.47 13.1或 14.
四、解答题
15题
(1)因为 ,且 ,所以 ,
解得, ,
综上所述, 的取值范围为 .
(2)由题意,需分为 和 两种情形进行讨论:
当 时, ,解得, ,满足题意;当 时,因为 ,所以 ,解得 ,
或 无解;
综上所述, 的取值范围为 .
16题
(1)由题函数 是定义在 上的奇函数,
所以 ,解得 ,
又由 ,得 ,解得 ,
所以 ,
(2) 在区间 上为增函数.
证明如下:
设 ,则 ,
由 ,
得 ,即 , , ,
所以 ,即 ,
所以函数 在 上单调递增.
17题
(1)不正确.
因为 ,所以 .
又 , 均为正数,所以 ,
当且仅当 ,即 时取等号.所以 ,当且仅当 ,即 ,时取等号.
综上, 的最小值为16.
多次连用基本不等式后,一定要注意验证等号成立的条件
(2)方法一:因为 ,所以
所以 .
当且仅当 且 时,即 , 时取等号.
综上, 的最小值为 .
方法二:
当且仅当 ,即 时等号成立.
18题
(1)因为二次函数 满足 ,
则 ,解得 .
所以
(2)若在 上,函数 的图象总在一次函数 的图象的上方,
则 在 上恒成立,即 在 上恒成立,
因为 开口向上,对称轴为 ,可知 在 上单调递减,
则 ,可得 ,
所以实数 的取值范围为 .
(3)因为 是对称轴为 ,开口向上的二次函数,
当 时, 在 上单调递增,则 ;
当 ,即 时, 在 上单调递减,
则 ;
当 ,即 时,
在 上单调递减,在 上单调递增,
可知 ;
综上所述: .
19题
(1) ;
(2)假设可以划分,
∵ ,∴ 和 一定是一个奇数一个偶数,
∴ , , , 中至多两个偶数.
则对于 的一种符合要求的划分 和 ,
每个四元子集中均有两个偶数.若两个集合分别为 和 ,
则 或49,不存在 , 使得 符合要求:
若两个集合分别为 和 ,
则 或13,不存在 , 使得 符合要求:
若两个集合分别为 和 ,
则 或25,不存在 , 使得 符合要求;
综上所述, 不能划分为两个不相交的“有趣的”四元子集,
(3)假设 可以划分为 个两两不相交的“有趣的”四元子集 , ,…, ,.
∵每个子集中至多两个偶数,又1,2,…, 中恰有 个偶数,
∴每个子集中均有两个偶数,
∴对于 ,可设 ,其中 , 是偶数, , 为奇数,
再由奇偶性,只能是 .
∵ ,
且 , .
∴ ,矛
盾.
∴ 不能划分为 个两两不相交的“有趣的”四元子集.