文档内容
高一数学试题
全卷满分150分 考试时间120分钟
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填
写在答题卡上.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应
位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按
以上要求作答的答案无效.
4.考生必须保持答题卡的整洁.考试结束后,将答题卡交回.
第I卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一
项是符合题目要求的.
1. 已知复数z满足 ,则z=( )
A. B.
C. D. 2-i
2. 若复数 对应的点是 ,则 ( )
A. B. C. -1 D. 1
3. 已知在平行四边形ABCD中, , ,对角线AC与BD相交于点M, (
)
A. B. C. D.
4. 在 中,若 , , ,则此三角形解的情况为( )
第1页/共7页
学科网(北京)股份有限公司A. 无解 B. 两解
C. 一解 D. 解的个数不能确定
5. 我国南北朝时期的数学家祖暅提出了一个原理“幂势既同,则积不容异”,即夹在两个平行平面之间的两
个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体
的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件,若该圆锥的侧面展开图是半径为2的一个半
圆,则该几何体的体积为( )
A. B. C. D.
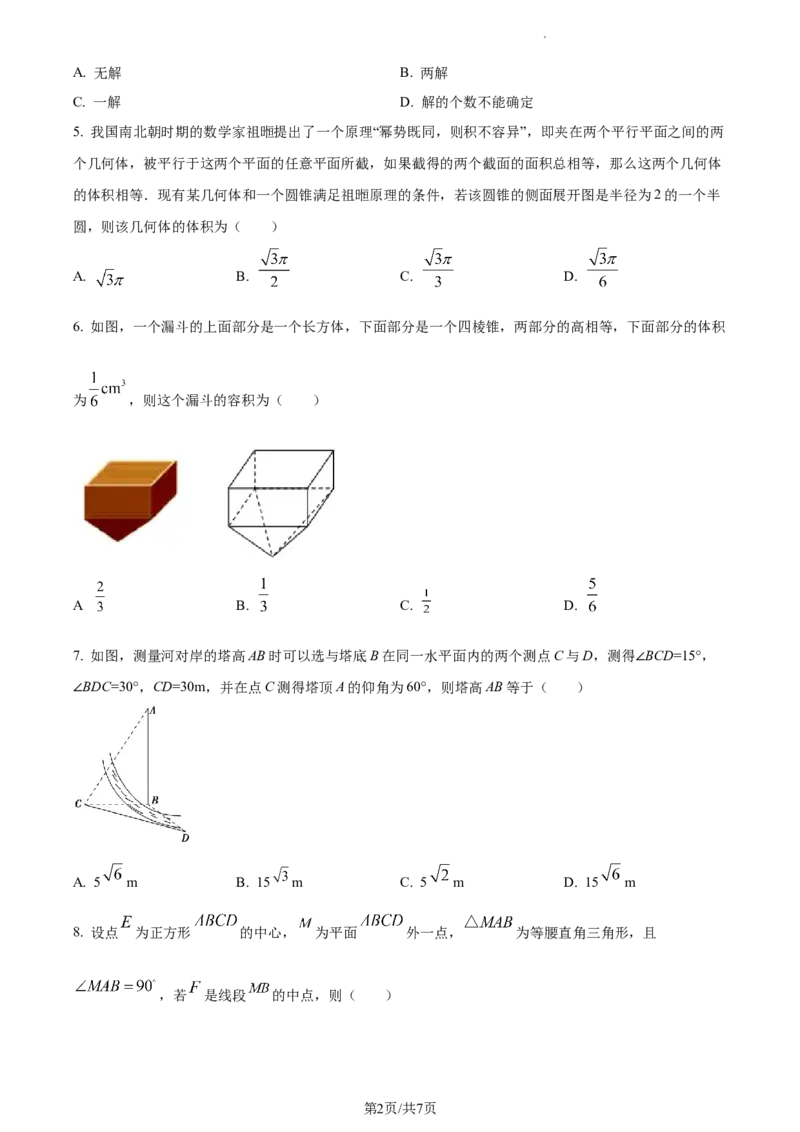
6. 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高相等,下面部分的体积
为 ,则这个漏斗的容积为( )
.
A B. C. D.
7. 如图,测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=15°,
∠BDC=30°,CD=30m,并在点C测得塔顶A的仰角为60°,则塔高AB等于( )
A. 5 m B. 15 m C. 5 m D. 15 m
8. 设点 为正方形 的中心, 为平面 外一点, 为等腰直角三角形,且
,若 是线段 的中点,则( )
第2页/共7页
学科网(北京)股份有限公司A. ,且直线 、 是相交直线
B. ,且直线 、 是相交直线
C. ,且直线 、 是异面直线
D. ,且直线 、 是异面直线
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 若一条直线与两个平行平面中的一个平行,则这条直线与另一个平面的位置关系为( )
A. 平行 B. 相交 C. 直线在平面内 D. 相切
10. 已知 为虚数单位,则以下四个说法中正确的是( )
的
A. B. 复数 虚部为
C. 若复数 为纯虚数,则 D. 若 为复数,则 为实数
11. 已知 中,其内角A,B,C的对边分别为a,b, 下列命题正确的有( )
A. 若 , , ,则
B. 若 , , ,则
C. 若A>B,则
D. 若 , ,则 外接圆半径为10
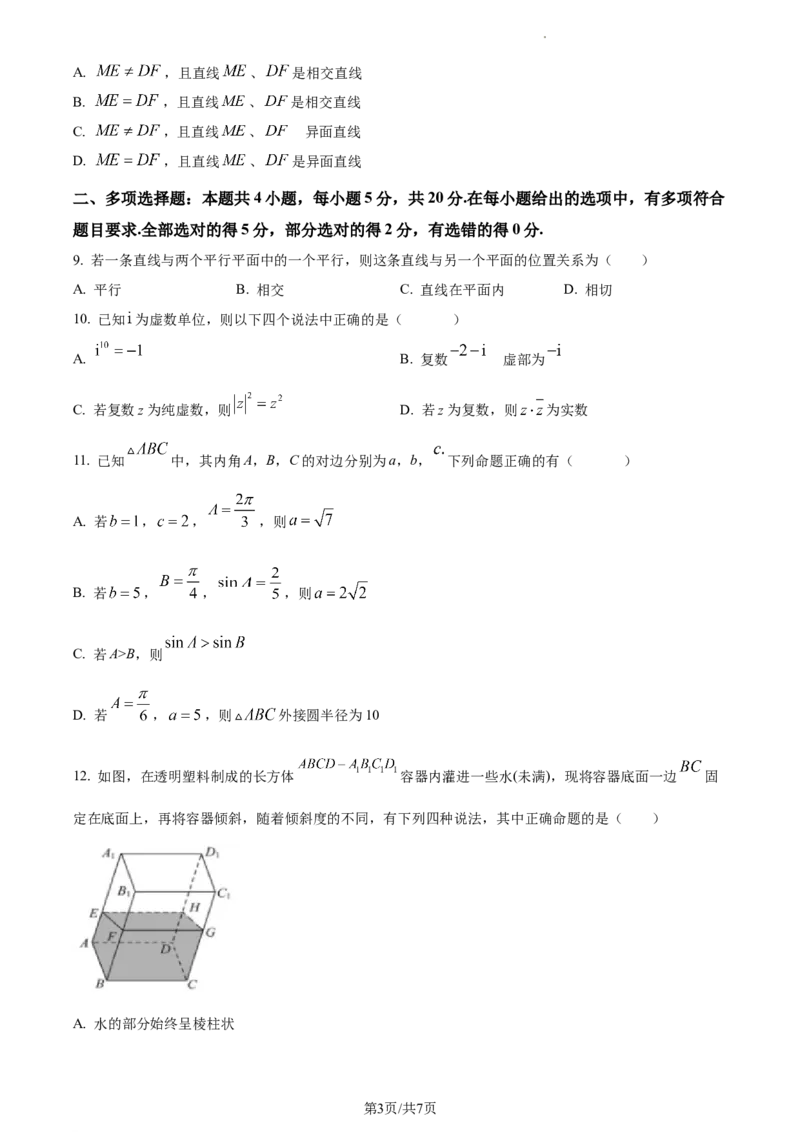
12. 如图,在透明塑料制成的长方体 容器内灌进一些水(未满),现将容器底面一边 固
定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法,其中正确命题的是( )
A. 水的部分始终呈棱柱状
第3页/共7页
学科网(北京)股份有限公司B. 水面四边形 的面积为定值
C. 棱 始终与水面 平行
D. 若 , ,则 是定值
第II卷
三.填空题:本题共4小题,每小题5分,共20分.
13. 已知向量 ,且 ,则 _______.
14. 已知正方体 的八个顶点在同一个球面上,若正方体的棱长是2,则球的表面积是
__________.
的
15. 若正四棱台 上底边长为2,下底边长为8,高为4,则它的侧面积为___________.
16. 已知 是钝角三角形,内角A,B,C所对的边分别为 , , , , ,则最大边 的
取值范围是_________.(结果用区间表示)
四.解答题:本题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤.
17. 知非零向量 和 不共线.
(1)如果 = + , =2 +8 , =3( - ),求证:A,B,D三点共线;
(2)欲使向量k + 与 +k 平行,试确定实数k的值.
18. 在 中,内角A,B,C对应的边分别为 , , ,已知 .
的
(1)求角B 大小;
(2)若 , 的面积为 ,求 的周长.
19. 如图,在棱长为2的正方体 中, 为棱 的中点.
第4页/共7页
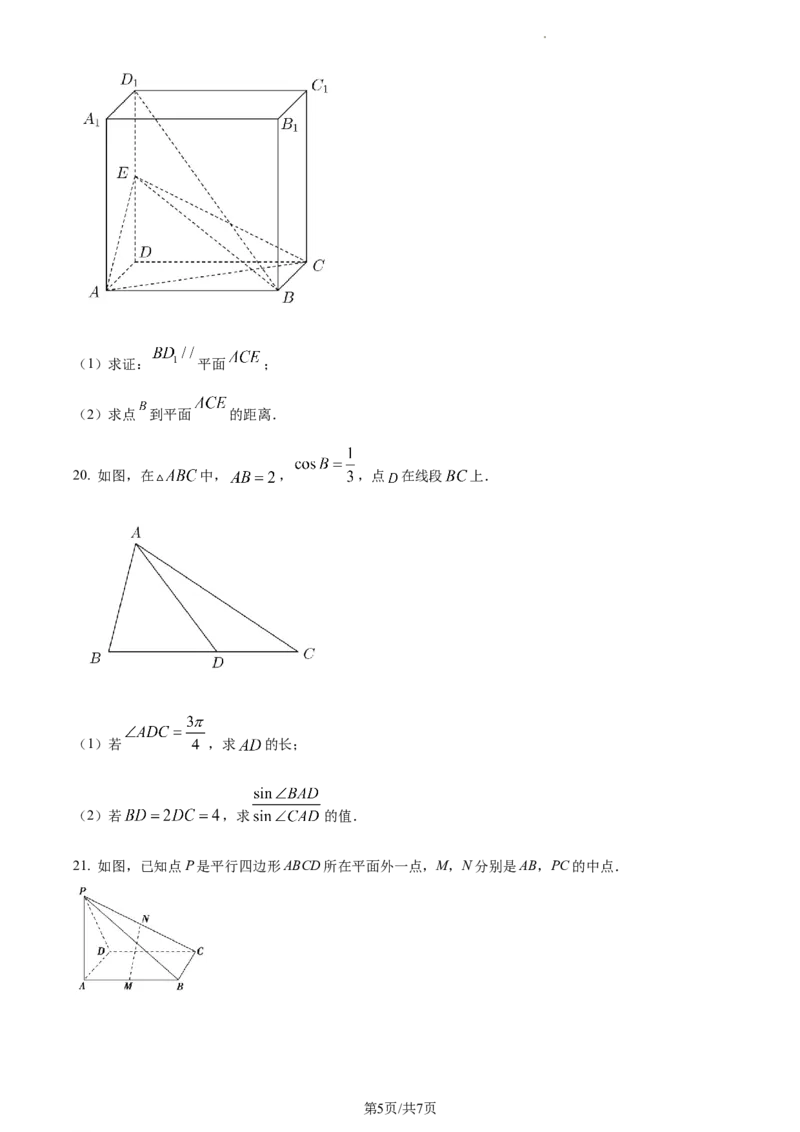
学科网(北京)股份有限公司(1)求证: 平面 ;
(2)求点 到平面 的距离.
20. 如图,在 中, , ,点 在线段 上.
(1)若 ,求 的长;
(2)若 ,求 的值.
21. 如图,已知点P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点.
第5页/共7页
学科网(北京)股份有限公司(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD,并证明你的结论.
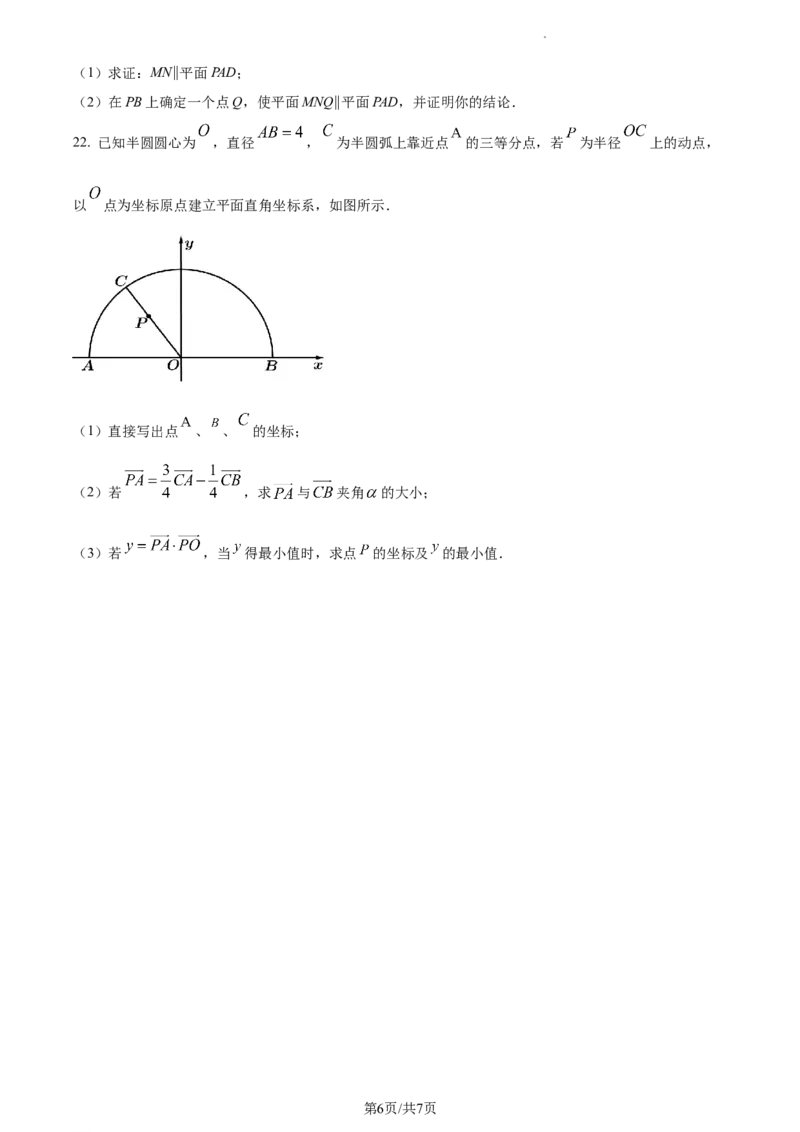
22. 已知半圆圆心为 ,直径 , 为半圆弧上靠近点 的三等分点,若 为半径 上的动点,
以 点为坐标原点建立平面直角坐标系,如图所示.
(1)直接写出点 、 、 的坐标;
(2)若 ,求 与 夹角 的大小;
(3)若 ,当 得最小值时,求点 的坐标及 的最小值.
第6页/共7页
学科网(北京)股份有限公司第7页/共7页
学科网(北京)股份有限公司