高二第一次月考备考金卷数学（B卷）-学生版_E015高中全科试卷_数学试题_选修1_05.月考测试_原创（新教材）上学期高二第一次月考备考金卷数学（B卷）

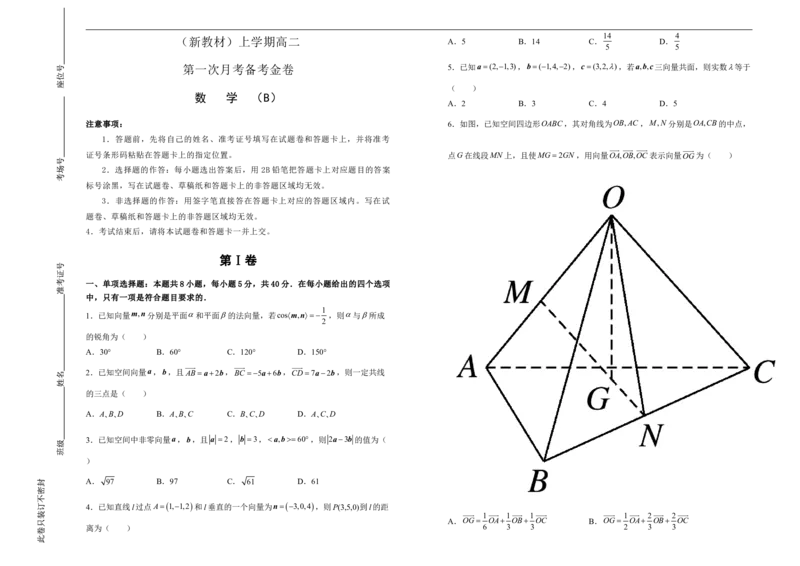
14 4 （新教材）上学期高二 A．5 B．14 C． D． 5 5 第一次月考备考金卷 5．已知a (2,1,3)，b(1,4,2)，c (3,2,)，若a,b,c三向量共面，则实数等于 （ ） 数 学 （B） A．2 B．3 C．4 D．5 注意事项： 6．如图，已知空间四边形OABC，其对角线为OB,AC，M,N 分别是OA,CB的中点， 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考     证号条形码粘贴在答题卡上的指定位置。 点G在线段MN 上，且使MG 2GN ，用向量OA,OB,OC 表示向量OG为（ ） 2．选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案 标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试 题卷、草稿纸和答题卡上的非答题区域均无效。 4．考试结束后，请将本试题卷和答题卡一并上交。 第Ⅰ卷 一、单项选择题：本题共8小题，每小题 5分，共40分．在每小题给出的四个选项 中，只有一项是符合题目要求的． 1 1．已知向量m,n分别是平面和平面的法向量，若cosm,n  ，则与所成 2 的锐角为（ ） A．30° B．60° C．120° D．150°    2．已知空间向量a，b，且ABa2b，BC 5a6b，CD7a2b，则一定共线 的三点是（ ） A．A､B､D B．A､B､C C．B､C､D D．A､C､D 3．已知空间中非零向量a，b，且 a 2， b 3，a,b60，则 2a3b 的值为（ ） A． 97 B．97 C． 61 D．61 4．已知直线l过点A1,1,2和l垂直的一个向量为n3,0,4，则P(3,5,0)到l的距  1 1 1  1 2 2 A．OG  OA OB OC B．OG  OA OB OC 离为（ ） 6 3 3 2 3 3 封封密密不不订订装装只只卷卷此此 号号位位座座 号号场场考考 号号证证考考准准 名名姓姓 级级班班  2 2  1 1 2 C．OG OA OB OC D．OG  OA OB OC A．a,b,x B．x,y,z C．b,c,z D．x,y,abc 3 3 2 3 3 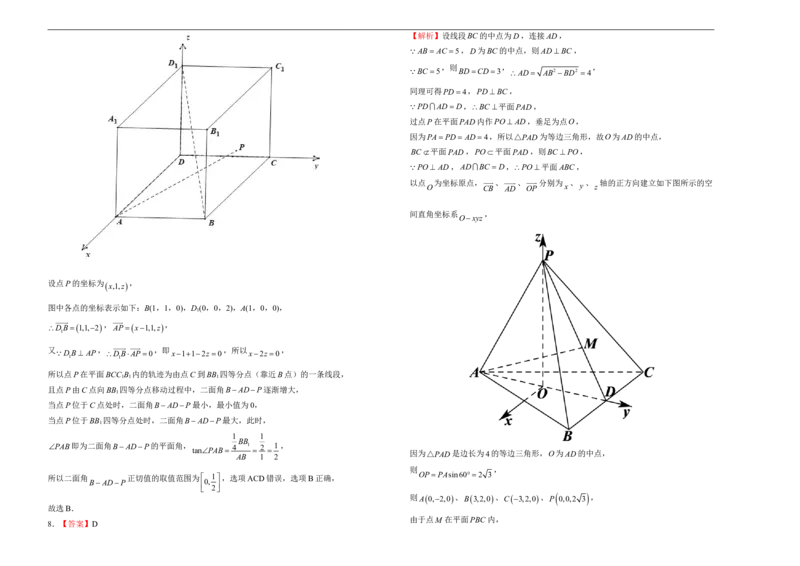7．长方体ABCDABC D ，AB BC 1，BB 2，点P在长方体的侧面BCC B 上 11．在长方体ABCDABC D 中，E､F ､G分别为棱AA ､C D ､DD 的中点， 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 运动，AP BD ，则二面角PADB的平面角正切值的取值范围是（ ） AB AA 2，AD1，则正确的选项是（ ） 1 1 A．异面直线EF 与BG所成角的大小为60°  1  1 1 1 1  A． 0, B． 0, C． , D． ,1          4  2 4 2 2  B．异面直线EF 与BG所成角的大小为90° 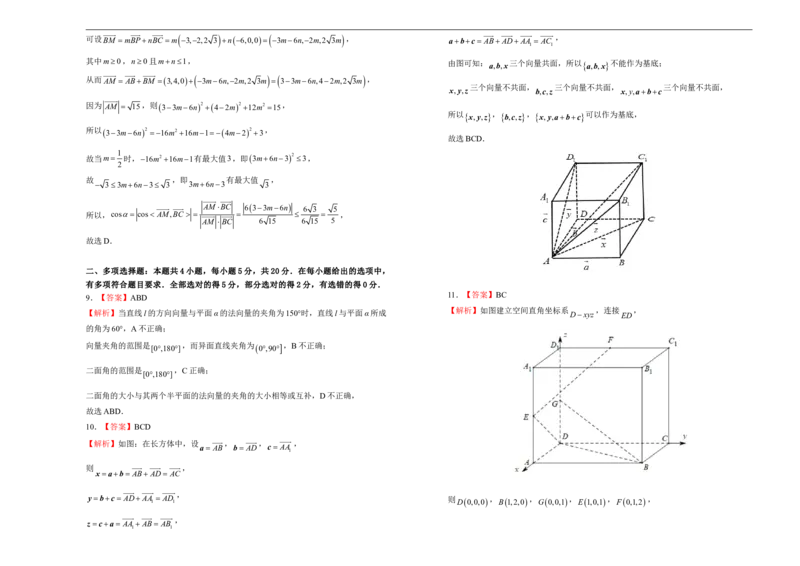8．如图，在三棱锥PABC 中，AB AC  PB PC 5，PA4，BC 6，点M 在 2 5 C．点E到平面BGD的距离为 5 平面PBC 内，且AM  15 ，设异面直线AM 与BC所成的角为，则cos的最大值 5 D．点E到平面BGD的距离为 为（ ） 5 12．已知E，F 分别是正方体ABCDABC D 的棱BC和CD的中点，则（ ） 1 1 1 1 2 3 2 5 A． B． C． D． 5 5 5 5 A．AD与BD 是异面直线 B．AD与EF 所成角的大小为45 1 1 1 1 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中， 1 6 有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． C．AF 与平面BEB所成角的余弦值为 D．二面角CDB B的余弦值为 1 1 3 1 1 3 9．下列说法不正确的是（ ） A．若直线l的方向向量与平面α的法向量的夹角等于150°，则直线l与平面α所成的 第Ⅱ卷 角等于30° 三、填空题：本大题共4小题，每小题5分． B．两条异面直线的夹角等于它们的方向向量的夹角 13．已知点 ， ， ， ，则在上的投影向量 A(1,1,0) B(1,2,0) C(2,1,0) D(3,4,0) AB CD C．二面角的大小范围是[0,180] 的长度为________． D．二面角的大小等于其两个半平面的法向量的夹角的大小 14．已知 ， ， ，点Q在直线OP上运动，则当 10．设a,b,c是空间的一个基底，若x ab， y bc，z ca．给出下列向量组 OA(1,2,3) OB(2,1,2) OP(1,1,2) 可以作为空间的基底的是（ ）  取得最小值时，点Q的坐标为（O为坐标原点）__________． 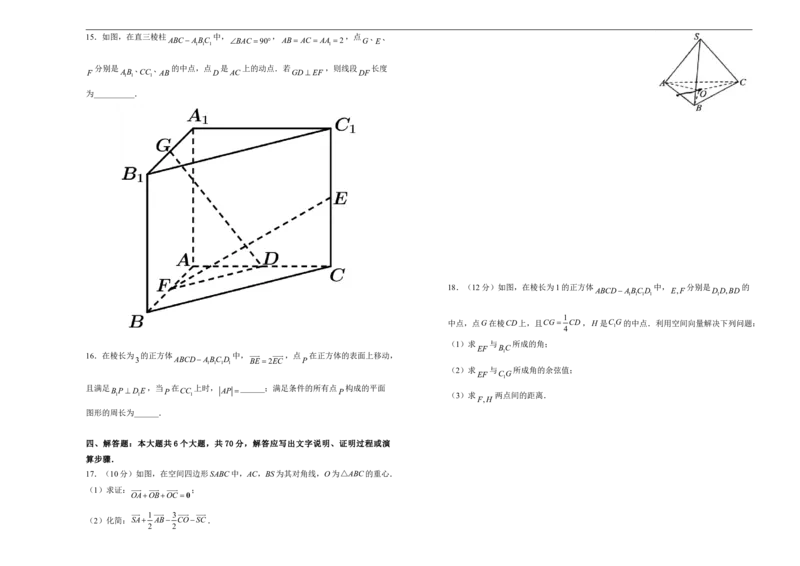QAQB15．如图，在直三棱柱 中， ， ，点 ､ ､ ABCABC BAC 90 AB AC  AA 2 G E 1 1 1 1 分别是 ､ ､ 的中点，点 是 上的动点．若 ，则线段 长度 F AB CC AB D AC GD EF DF 1 1 1 为__________． 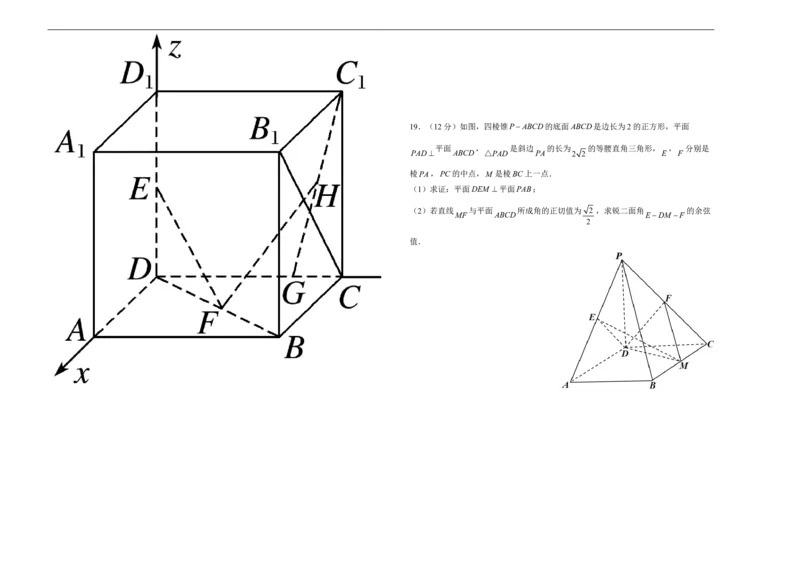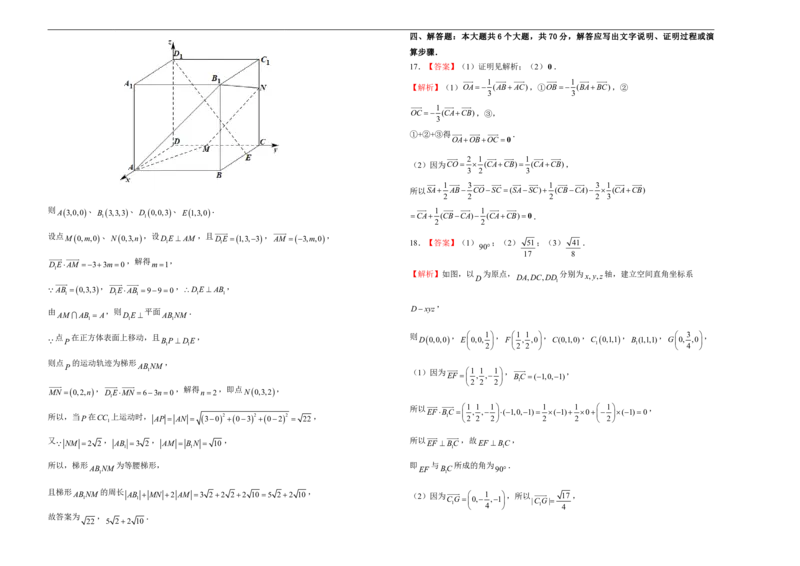18．（12分）如图，在棱长为1的正方体 中， 分别是 的 ABCDABC D E,F DD,BD 1 1 1 1 1 1 中点，点G在棱CD上，且CG  CD，H 是CG的中点．利用空间向量解决下列问题： 4 1 （1）求 与 所成的角； EF BC 1 16．在棱长为 的正方体 中， ，点 在正方体的表面上移动， 3 ABCDABC D BE 2EC P 1 1 1 1 （2）求 与 所成角的余弦值； EF CG 1 且满足 ，当 在 上时， ______；满足条件的所有点 构成的平面 BP  DE P CC AP  P 1 1 1 （3）求 两点间的距离． F,H 图形的周长为______． 四、解答题：本大题共 6 个大题，共 70 分，解答应写出文字说明、证明过程或演 算步骤． 17．（10分）如图，在空间四边形SABC中，AC，BS为其对角线，O为△ABC的重心． （1）求证：   ； OAOBOC 0  1 3  （2）化简：SA AB COSC． 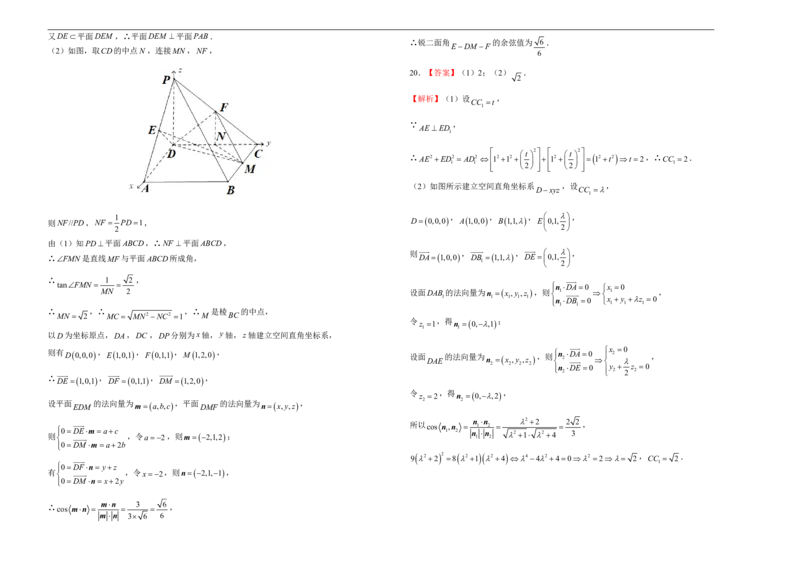2 219．（12分）如图，四棱锥PABCD的底面ABCD是边长为2的正方形，平面 平面 ， 是斜边 的长为 的等腰直角三角形， ， 分别是 PAD ABCD △PAD PA 2 2 E F 棱PA，PC的中点，M 是棱BC上一点． （1）求证：平面DEM 平面PAB； （2）若直线 与平面 所成角的正切值为 2 ，求锐二面角 的余弦 MF ABCD EDM F 2 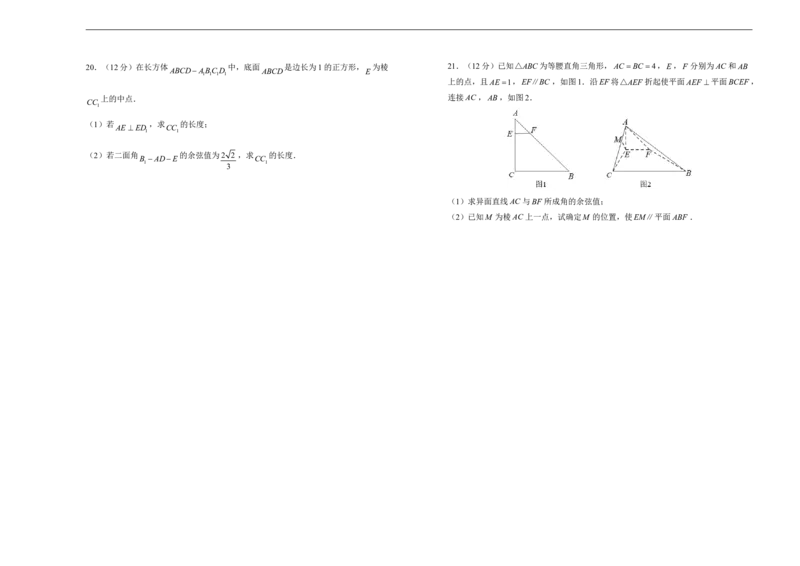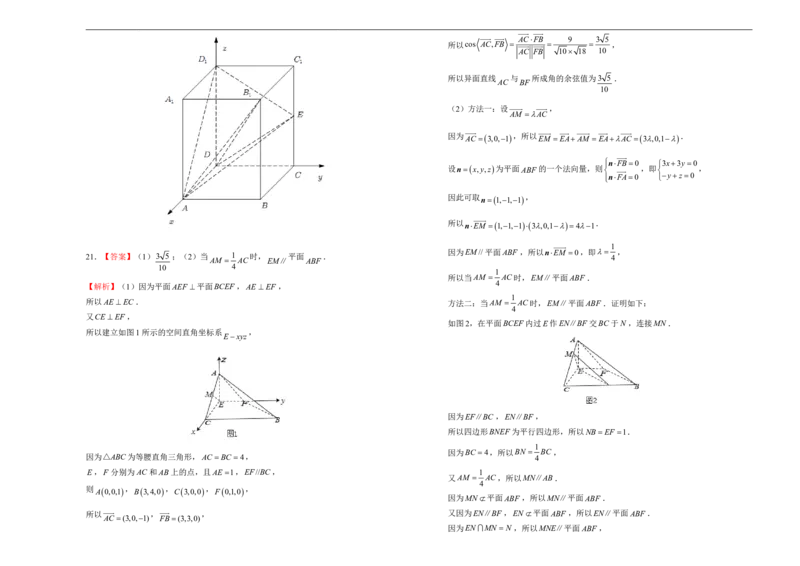值．20．（12分）在长方体 中，底面 是边长为1的正方形， 为棱 21．（12分）已知△ABC为等腰直角三角形，AC  BC 4，E，F 分别为AC 和AB ABCDABC D ABCD E 1 1 1 1 上的点，且AE 1，EF∥BC ，如图1．沿EF将△AEF 折起使平面AEF 平面BCEF， 上的中点． 连接AC ，AB，如图2． CC 1 （1）若 ，求 的长度； AE  ED CC 1 1 （2）若二面角 的余弦值为2 2 ，求 的长度． B ADE CC 1 1 3 （1）求异面直线AC 与BF 所成角的余弦值； （2）已知M 为棱AC 上一点，试确定M 的位置，使EM∥平面ABF ．22．（12分）在①OH//平面PAB，②平面PAB平面OHC，③OH  PC这三个条件 中任选一个，补充在下面的问题中，并解决该问题． 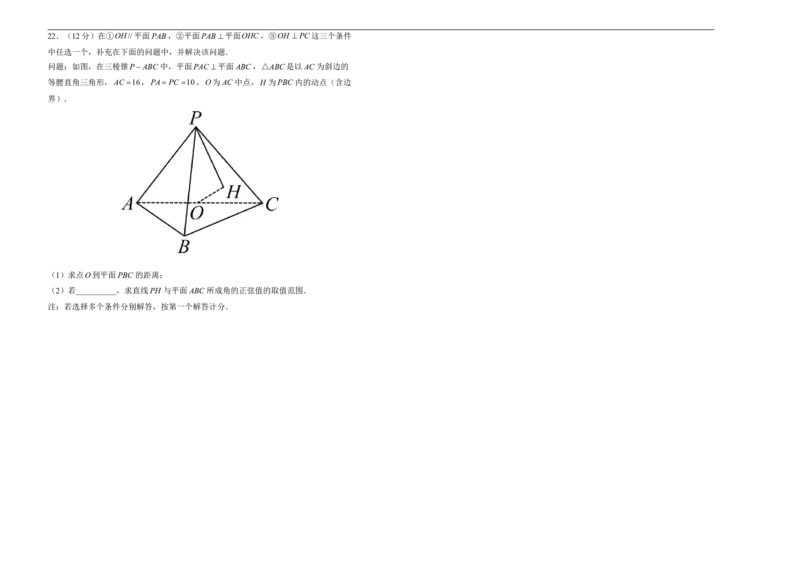问题：如图，在三棱锥PABC 中，平面PAC 平面ABC，△ABC是以AC 为斜边的 等腰直角三角形，AC 16，PA PC 10，O为AC 中点，H 为PBC 内的动点（含边 界）． （1）求点O到平面PBC 的距离； （2）若__________，求直线PH 与平面ABC所成角的正弦值的取值范围． 注：若选择多个条件分别解答，按第一个解答计分．（新教材）2021-2022 学年上学期高二 【解析】∵ P  A  2,6,2， P  A  n2,6,23,0,414 ， n 5 ，  PAn 第一次月考备考金卷 14 ∴点P到直线l的距离为 d   ． n 5 数 学 （B） 答 案 5．【答案】C 【解析】∵a与b不共线，则取a，b作为平面的一组基向量， 第Ⅰ卷 又 三向量共面，则存在实数 使得 ， a,b,c , c ab 1 2 1 2 一、单项选择题：本题共8小题，每小题 5分，共40分．在每小题给出的四个选项 32 2 1 2 1   中，只有一项是符合题目要求的． ∴ 24 ，解得  1，故选C． 1 2 2   1．【答案】B  32  4 1 2 【解析】设 与 所成的角为θ，且0°<θ<90°，   6．【答案】A     2 2 1 1 【解析】OG OM MG OM  MN  ON  OM ， 则cos cosm,n  ，60，故选B． 3 3 3 2 因为 分别为 的中点， 2．【答案】A M,N OA,CB 【解析】因为 B  D    B  C  C  D  2a4b2  A  B ，所以 B  D  ∥  A  B ， 所以O  M   1 O  A  ，O  N   1 O  B  O  C  ， 2 2 又 B  D  ,  A  B 有公共点 B ，所以A､B､D三点共线，故选项A正确；  1  1 1 1 1 所以OG  OBOC  OA OA OB OC，故选A． 3 6 6 3 3 显然 A  B  ,  B  C 不共线，所以 A 、 B 、 C 三点不共线，故选项B错误； 7．【答案】B 【解析】如图以点D为坐标原点建立空间直角坐标系， 显然 不共线，所以 、 、 三点不共线，故选项C错误； BC,CD B C D 因为   ，所以 不共线，从而 、 、 三点不共线， AC  ABBC 4a8b AC,CD A C D 故选项D错误， 故选A． 3．【答案】C 【解析】∵ 2a3b 2 2a3b2 4a2 9b2 12ab449912 a  b cos60 1 971223 61， 2 ∴ ，故选C． 2a3b  61 4．【答案】C【解析】设线段BC的中点为D，连接AD， AB AC 5，D为BC的中点，则AD BC ，  ，则 ， ，  BC 5 BDCD3 AD AB2 BD2 4 同理可得PD4，PD BC， PD AD D，BC 平面PAD，   过点P在平面PAD内作PO AD，垂足为点O， 因为PA PD AD4，所以△PAD为等边三角形，故O为AD的中点， BC 平面PAD，PO平面PAD，则BC  PO， PO AD，AD BC  D，PO平面ABC，   以点 O 为坐标原点， C  B 、 A  D 、 O  P 分别为 x 、 y 、 z 轴的正方向建立如下图所示的空 间直角坐标系 ， Oxyz 设点P的坐标为x,1,z， 图中各点的坐标表示如下：B(1，1，0)，D (0，0，2)，A(1，0，0)， 1   D  B  1,1,2， A  P  x1,1,z， 1 又 ，   ，即 ，所以 ， DB  AP DBAP 0 x112z 0 x2z 0  1 1 所以点P在平面BCC B 内的轨迹为由点C到BB 四等分点（靠近B点）的一条线段， 1 1 1 且点P由C点向BB 四等分点移动过程中，二面角BADP逐渐增大， 1 当点P位于C点处时，二面角BADP最小，最小值为0， 当点P位于BB 四等分点处时，二面角BADP最大，此时， 1 1 1 BB PAB即为二面角BADP的平面角， 4 1 2 1 ， tanPAB   因为△PAD是边长为4的等边三角形，O为AD的中点， AB 1 2 则 ， 所以二面角 正切值的取值范围为 1，选项ACD错误，选项B正确， OP PAsin602 3 BADP 0,    2 则A0,2,0、B3,2,0、C3,2,0、P  0,0,2 3 ， 故选B． 由于点M 在平面PBC 内， 8．【答案】D可设  B  M  m  B  P  n  B  C  m  3,2,2 3  n6,0,0  3m6n,2m,2 3m ， abc   A  B    A  D    A  A    A  C ， 1 1 其中m0，n0且mn1， 由图可知： a,b,x 三个向量共面，所以a,b,x不能作为基底； 从而  A  M    A  B    B  M  3,4,0  3m6n,2m,2 3m    33m6n,42m,2 3m ， 三个向量不共面， 三个向量不共面， 三个向量不共面， x,y,z b,c,z x,y,abc  因为 AM  15，则33m6n2 42m2 12m2 15 ， 所以x,y,z，b,c,z，x,y,abc可以作为基底， 所以33m6n2 16m2 16m14m22 3 ， 故选BCD． 1 故当m 时，16m2 16m1有最大值3，即3m6n32 3， 2 故 ，即 有最大值 ，  33m6n3 3 3m6n3 3     AM BC 633m6n 6 3 5 所以，cos cos AM,BC      ，   AM  BC 6 15 6 15 5 故选D． 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中， 有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 11．【答案】BC 9．【答案】ABD 【解析】如图建立空间直角坐标系 ，连接 ， 【解析】当直线l的方向向量与平面α的法向量的夹角为150°时，直线l与平面α所成 Dxyz ED 的角为60°，A不正确； 向量夹角的范围是 [0,180] ，而异面直线夹角为0,90，B不正确； 二面角的范围是 ，C正确； [0,180] 二面角的大小与其两个半平面的法向量的夹角的大小相等或互补，D不正确， 故选ABD． 10．【答案】BCD 【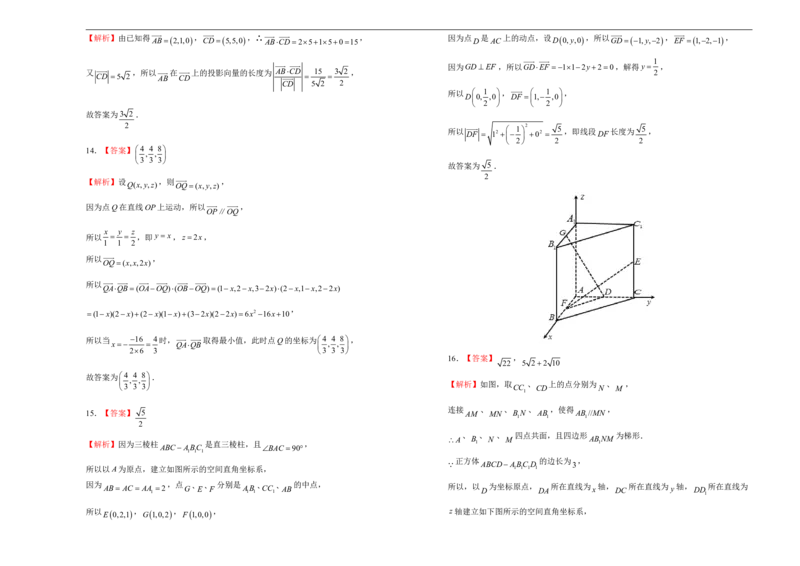解析】如图：在长方体中，设 ， ，  ， a  AB b AD c  AA 1 则   ， x ab AB AD AC   ， y bc  AD AA 1  AD 1 则 D0,0,0， B1,2,0， G0,0,1， E1,0,1， F0,1,2，    ， z ca  AA  AB AB 1 1  所以 E  F  1,1,1， B  G  1,2,1， ADEF 2 1 1 设AD与EF 所成角为，则cos   ， 1  A  D    E  F  8 2 2 1 所以  ，所以 ， EFBG 1210 EF  BG 又因为090，所以60，故B错误； 所以异面直线EF 与BG所成角的大小为90°，故A错误，B正确； 对选项C，由题知：平面 的法向量为， BEB DC 1 又 D  E  1,0,1， D  B  1,2,0， 因为 D  C  0,2,0， A  F  2,1,2， 1 设平面 BGD 的一个法向量 m x,y,z， 设 与平面 所成角为 ， AF BEB  1 1   mBG x2yz 0 则   ，令y 1，则m 2,1,0，  A  F    D  C  mDB x2y 0 则sin  1    2  1 ，cos 2 2 ，故C错误； AF  DC 2 9 3 3 1  DEm 2 2 5 则点 E 到平面 BGD 的距离为 m  5  5 ，故C正确，D错误， 对选项D， D  B  2,2,0， B  B  0,0,2， 1 1 1 故选BC． 设平面 DBB 的法向量 m x ,y ,z ， 1 1 1 1 1 12．【答案】AD  【解析】对选项A，由图知： 与 是异面直线，故A正确；  mDB 2x 2y 0 A 1 D B 1 D 1 则   1  1 1 1 ，令x 1 1，得m 1,1,0；  mBB 2z 0 1 1 以 为原点， ， ， 分别为 ， ， 轴建立空间直角坐标系， D DA DC DD 1 x y z 设平面 DBC 的法向量 nx ,y ,z ， B  C  2,0,2， 1 1 2 2 2 1 设正方体边长为2，   nDB 2x 2y 0 对选项B， 则   1  1 2 2 ，令x 2 1，得n1,1,1，  nBC 2x 2z 0 1 2 2 mn 2 6 设二面角 的平面角为 ，则 ， CDB B  cos   1 1 m  n 2 3 3 又因为 为锐角，所以 6 ，故D正确，  cos 3 故选AD． 第Ⅱ卷 D0,0,0， A 2,0,2， E1,2,0， F0,1,0， 1 三、填空题：本大题共4小题，每小题5分． 所以 A  D  2,0,2， E  F  1,1,0， 1 13．【答案】3 2 2【解析】由已知得 A  B  2,1,0， C  D  5,5,0，∴ A  B  C  D  2515015 ， 因为点 D 是 AC 上的动点，设 D0,y,0，所以 G  D  1,y,2， E  F  1,2,1，   1   因为GD EF ，所以GDEF 112y20，解得y  ， 又  ，所以在上的投影向量的长度为 ABCD 15 3 2 ， 2 CD 5 2 AB CD    CD 5 2 2 所以  1 ，  1 ， D 0, ,0 DF  1, ,0      2   2  故答案为3 2 ． 2 2 所以  D  F   12    1 02  5 ，即线段 DF 长度为 5 ，    2 2 2 14．【答案】4 4 8 , ,   3 3 3 故答案为 5 ． 2 【解析】设 ，则 ， Q(x,y,z) OQ(x,y,z) 因为点Q在直线OP上运动，所以 ， OP∥OQ x y z 所以   ，即y  x，z 2x， 1 1 2 所以 ， OQ(x,x,2x) 所以      QAQB(OAOQ)(OBOQ)(1x,2x,32x)(2x,1x,22x) ， (1x)(2x)(2x)(1x)(32x)(22x)6x2 16x10 所以当 16 4时， 取得最小值，此时点Q的坐标为4 4 8， x  QAQB  , ,  26 3 3 3 3 16．【答案】 ， 22 5 22 10 故答案为4 4 8． , ,   【解析】如图，取 、 上的点分别为 、 ， 3 3 3 CC CD N M 1 连接 、 、 、 ，使得 ， 15．【答案】 5 AM MN BN AB AB //MN 1 1 1 2 、 、 、 四点共面，且四边形 为梯形． A B N M ABNM 【解析】因为三棱柱 是直三棱柱，且 ， 1 1 ABCABC BAC 90 1 1 1 正方体 的边长为 ， ABCDABC D 3 所以以A为原点，建立如图所示的空间直角坐标系，  1 1 1 1 因为 AB AC  AA 2 ，点 G ､ E ､ F 分别是 AB ､ CC ､ AB 的中点， 所以，以 D 为坐标原点， DA 所在直线为 x 轴， DC 所在直线为 y 轴， DD 所在直线为 1 1 1 1 1 所以 E0,2,1， G1,0,2， F1,0,0， z 轴建立如下图所示的空间直角坐标系，四、解答题：本大题共 6 个大题，共 70 分，解答应写出文字说明、证明过程或演 算步骤． 17．【答案】（1）证明见解析；（2）0．  1    1   【解析】（1）OA (AB AC)，①OB (BABC)，② 3 3  1   OC  (CACB)，③， 3 ①+②+③得   ． OAOBOC 0  2 1   1   （2）因为CO  (CACB) (CACB)， 3 2 3  1 3    1   3 1   所以SA AB COSC (SASC) (CBCA)  (CACB) 2 2 2 2 3 则 A3,0,0、 B 3,3,3、 D 0,0,3、 E1,3,0．  1   1   1 1 CA (CBCA) (CACB)0． 2 2 设点 M 0,m,0、 N0,3,n，设 DE  AM ，且 D  E  1,3,3， A  M  3,m,0， 1 1 18．【答案】（1） ；（2） 51；（3） 41 ． 90 17 8   ，解得 ， DEAM 33m0 m1 1 【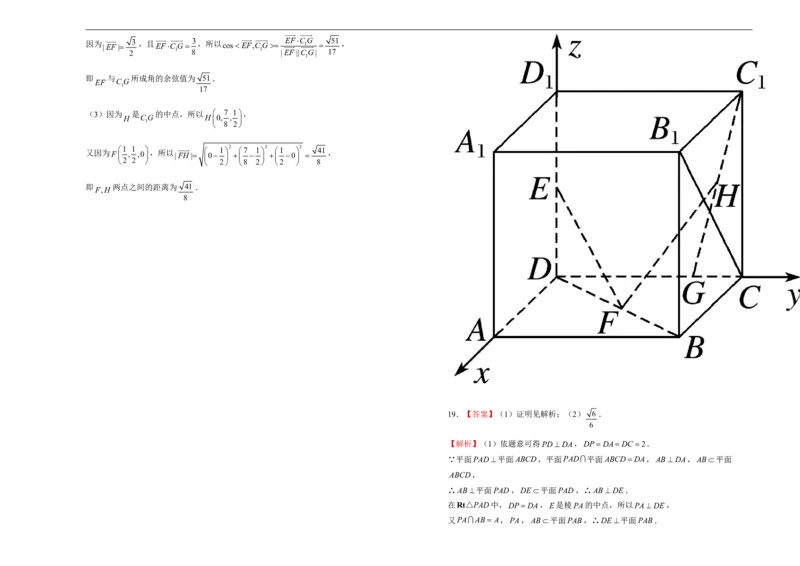解析】如图，以 为原点， 分别为 轴，建立空间直角坐标系 D DA,DC,DD x,y,z 1  A  B  0,3,3， D  E    A  B  990 ， DE  AB ，  1 1 1 1 1 ， Dxyz 由 ，则 平面 ． AM AB  A DE  ABNM  1 1 1  点 P 在正方体表面上移动，且 B 1 P  D 1 E ， 则 D0,0,0 ， E    0,0, 1 2    ， F    1 2 , 1 2 ,0    ， C(0,1,0) ， C 1 0,1,1 ， B 1 (1,1,1) ， G    0, 3 4 ,0    ， 则点 的运动轨迹为梯形 ， P ABNM 1 （1）因为 1 1 1， ， EF   , ,  BC (1,0,1) 2 2 2 1 M  N  0,2,n， D  E  M  N  63n0 ，解得 n2 ，即点 N0,3,2， 1 所以  1 1 1 1 1  1 ， EFBC  , , (1,0,1) (1) 0  (1)0     所以，当P在CC 上运动时， AP  AN  302 032 022  22 ， 1 2 2 2 2 2  2 1 又 ， ， ， 所以 ，故 ， NM 2 2 AB 3 2 AM  BN  10 EF  BC EF  BC  1 1 1 1 所以，梯形 为等腰梯形， 即 与 所成的角为 ． ABNM EF BC 90 1 1 且梯形 的周长 ， ABNM AB  MN 2 AM 3 22 22 10 5 22 10 （2）因为  1 ，所以  17 ， 1 1 CG   0, ,1  |CG| 1  4  1 4 故答案为 ， ． 22 5 22 10  因为 |  E  F  | 3 ，且 E  F  C  G   3 ，所以 cos  E  F  ,C  G    E  F  C  1 G   51 ， 2 1 8 1 |EF ||CG| 17 1 即 与 所成角的余弦值为 51． EF CG 1 17 （3）因为 是 的中点，所以  7 1， H CG H  0, ,  1  8 2 又因为F   1 , 1 ,0   ，所以 |  F  H  |   0 1  2    7  1  2    1 0   2  41 ， 2 2   2 8 2 2  8 即 两点之间的距离为 41 ． F,H 8 19．【答案】（1）证明见解析；（2） 6 ． 6 【解析】（1）依题意可得PD DA，DP DA DC 2． ∵平面PAD平面ABCD，平面PAD 平面ABCD DA，AB DA，AB平面  ABCD， ∴AB平面PAD，DE 平面PAD，∴AB DE． 在Rt△PAD中，DP DA，E是棱PA的中点，所以PA DE， 又PA AB  A，PA，AB平面PAB，∴DE 平面PAB． 又DE 平面DEM ，∴平面DEM 平面PAB． ∴锐二面角 的余弦值为 6 ． EDM F （2）如图，取CD的中点N ，连接MN ，NF ， 6 20．【答案】（1）2；（2） ． 2 【解析】（1）设 ， CC t 1 ∵ ， AE  ED 1 ∴AE2 ED2  AD2   12 12    t   2   12    t   2    12 t2 t 2，∴CC 2． 1 1  2   2  1 （2）如图所示建立空间直角坐标系 ，设 ， Dxyz CC  1 1 ， ， ，  ， 则NF//PD，NF  PD1， D0,0,0 A1,0,0 B1,1, E  0,1,  2  2 由（1）知PD平面ABCD，∴NF 平面ABCD， 则 ， ，  ， ∴FMN 是直线MF与平面ABCD所成角， DA1,0,0 DB 1,1, DE   0,1,  1  2 ∴ 1 2 ，  tanFMN    n DA0 x 0 MN 2 设面DAB 1 的法向量为n 1 x 1 ,y 1 ,z 1 ，则   n 1 1   D  B  1 0   x 1 1  y 1 z 1 0 ， ∴ ，∴ ，∴ 是棱 的中点， MN  2 MC  MN2 NC2 1 M BC 令 z 1 ，得 n 0,,1； 1 1 以D为坐标原点，DA，DC ，DP分别为x轴，y轴，z 轴建立空间直角坐标系，  x 0 则有 D0,0,0， E1,0,1， F0,1,1， M 1,2,0， 设面 DAE 的法向量为 n 2 x 2 ,y 2 ,z 2 ，则     n n 2 2    D D  A E    0 0      y 2 2   2 z 2 0 ， ∴ D  E  1,0,1， D  F  0,1,1， D  M  1,2,0， 令 z 2 ，得 n 0,,2， 2 2 设平面 EDM 的法向量为 m a,b,c，平面 DMF 的法向量为 nx,y,z， n n 2 2 2 2  所以 cos n ,n  1 2   ， 则    0 DEm ac ，令a2，则m 2,1,2； 1 2 n 1  n 2 2 1 2 4 3  0 DM m a2b 9  2 2 2 8  2 1  2 4  4 42 402 2 2 ， CC  2 ．  1  0 DFn yz 有  ，令x2，则n2,1,1，  0 DM n x2y mn 3 6 ∴ ， cos mn    m  n 3 6 6    ACFB 9 3 5 所以cos AC,FB    ，   AC FB 10 18 10 所以异面直线 与 所成角的余弦值为3 5 ． AC BF 10 （2）方法一：设 ， AM AC 因为 A  C  3,0,1，所以 E  M    E  A    A  M    E  A    A  C  3,0,1．   nFB0 3x3y 0 设nx,y,z为平面ABF 的一个法向量，则  ，即  ，  nFA0 yz 0 因此可取 n1,1,1， 所以 n  E  M  1,1,13,0,141 ．  1 因为EM//平面ABF ，所以nEM 0，即 ， 21．【答案】（1）3 5 ；（2）当 1 时， 平面 ． 4 AM  AC EM∥ ABF 10 4 1 所以当AM  AC时，EM∥平面ABF ． 4 【解析】（1）因为平面AEF 平面BCEF，AE  EF ， 1 所以AE  EC． 方法二：当AM  AC时，EM∥平面ABF ．证明如下： 4 又CE  EF ， 如图2，在平面BCEF内过E作EN∥BF 交BC于N ，连接MN ． 所以建立如图1所示的空间直角坐标系 ， Exyz 因为EF∥BC ，EN∥BF ， 所以四边形BNEF为平行四边形，所以NB EF 1． 1 因为BC 4，所以BN  BC ， 因为△ABC为等腰直角三角形，AC  BC 4， 4 E，F 分别为AC 和AB上的点，且AE 1，EF//BC， 1 又AM  AC，所以MN∥AB． 4 则 A0,0,1， B3,4,0， C3,0,0， F0,1,0， 因为MN 平面ABF ，所以MN∥平面ABF ． 所以 ， ， 又因为EN∥BF ，EN 平面ABF ，所以EN∥平面ABF ． AC (3,0,1) FB(3,3,0) 因为EN MN  N ，所以MNE∥平面ABF ， 因为EM 平面MNE，所以EM∥平面ABF ．   n PA0 设平面PAB的法向量为n 1 x 1 ,y 1 ,z 1 ，则  1  ， 22．【答案】（1） 12 34 ；（2）   3 ， 3 17  ．  n 1 PB0 17  5 17  8y 6z 0 x y 即 1 1 ，即 1 1 ，   【解析】（1）在三棱锥PABC 中，连接OB，OP， 8x 6z 0 4y 3z   1 1 1 1 因为△ABC是以AC 为斜边的等腰直角三角形，PA PC，O为AC 中点， 不妨令 y 3 ，则 n 3,3,4； 所以OPOC，OBOC， 1 1 又平面PAC 平面ABC，平面PAC 平面ABC OC，OP平面PAC ，  同理可求得平面 PBC 的法向量 n 3,3,4， 2 ∴OP平面ABC， （选条件①）因为OH∥平面PAB，PH 平面PBC ， 又OB平面ABC，∴OPOB，∴OB，OC ，OP两两垂直．   OHn 0 3x3y4z 0 ∴ V OPBC V POBC  1 3 POS △OBC  1 3  102 82  1 2     1 2 6   2 ， ∴    P  H  n 1 2 0 ，即  3x3y4z240 ，  3 又 S  1 BC PB2    BC  2  1 8 2 102   4 2 2 8 34 ， 即  z 3 4 x ，∴ H   x,4,3 3 x   ， △PBC 2  2  2  y 4  4  V 64 12 34 ∴d  OPBC   ， 0 x8 1 1 17 又 ，∴ ，∴  3 ， S 8 34  3 0 x4 PH   x,4,3 x  3 △PBC 3  03 x6  4   4 ∴点 O 到平面 PBC 的距离为12 34 ． 又 OP 平面 ABC ，∴ n 0,0,1是平面 ABC 的一个法向量， 17 3 设直线PH 与平面ABC所成角为， 3 3 17 （2） PH 与平面 ABC 所成角的正弦值的取值范围为  ,  ． 5 17 3  x   |3 x| 3  1   4  4 则sin cos n ,PH   ， 3 以选条件①为例（亦可使用综合法、综合与向量混用法） 2 2  3  x  32 x  32 x2 16 3 5 1  1        在三棱锥 PABC 中，以 O 为坐标原点， O  B  ,O  C  ,O  P 为正交基底，  4 4  254  50 建立空间直角坐标系 ， 令 t  x 1 ， t1,2，1  1 ,1 ， Oxyz   4 t 2  则 O0,0,0， P0,0,6， A0,8,0， C0,8,0， B8,0,0， 3t 3 sin  ∴ ， 32 32 32 32 5 t2  t 5  1 设 Hx,y,z，则 O  H  x,y,z， P  H  x,y,z6， P  A  0,8,6， 25 25 25t2 25t  P  B  8,0,6， P  C  0,8,6， 令 f 1  32  1  32  1 1 ，则 1  1 ，   t 25 t2 25 t t 2 0维权 声明 ∴ 1在1 上单调递增， f ,1     t 2  1  25 ∴ f   1     17 ,1   ，∴ 1    1, 17   ，∴ sin   3 , 3 17  ， t 25  f    5 17  t 3 3 17 ∴直线 PH 与平面 ABC 所成角的正弦值的取值范围为  ,  ． 5 17   选条件②，条件③结果相同．