高二第一次月考备考金卷数学（A卷）-学生版_E015高中全科试卷_数学试题_选修1_05.月考测试_原创（新教材）上学期高二第一次月考备考金卷数学（A卷）

（新教材）上学期高二
①
A

B



B

C

C

C
 ；②
A

B



B

C



D

D
 ；③
A

B



A

D

C

C

；
1 1 1
第一次月考备考金卷
④
A

B



A

D



D

D
 ；⑤
A

B



A

A



A

D
 ；⑥
A

B



A

D



A

A

．
1 1 1 1 1
A．3个 B．4个 C．5个 D．6个
数 学 （A）
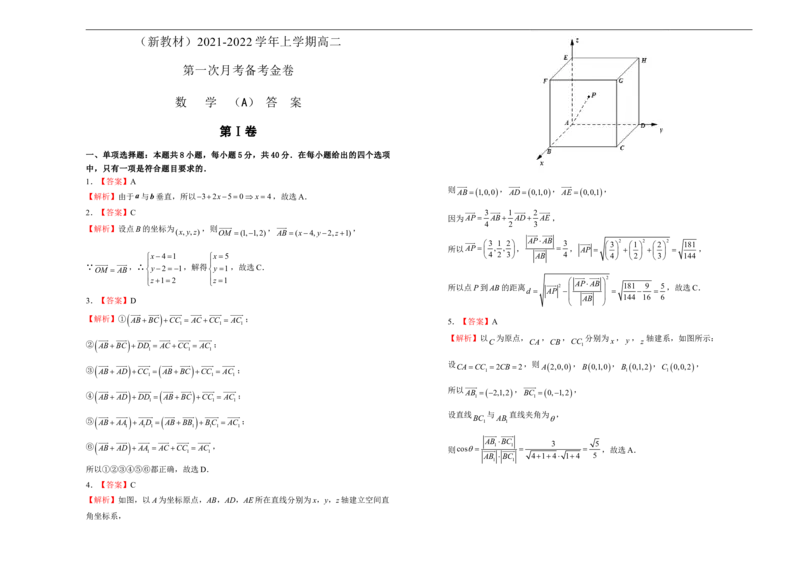
4．如图，ABCDEFGH 是棱长为1的正方体，若P在正方体内部且满足
注意事项：
，则P到AB的距离为（ ）
1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考
证号条形码粘贴在答题卡上的指定位置。
2．选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案
标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试
题卷、草稿纸和答题卡上的非答题区域均无效。
4．考试结束后，请将本试题卷和答题卡一并上交。
第Ⅰ卷
3 4 5 3
A． B． C． D．
一、单项选择题：本题共8小题，每小题 5分，共40分．在每小题给出的四个选项 4 5 6 5
中，只有一项是符合题目要求的．
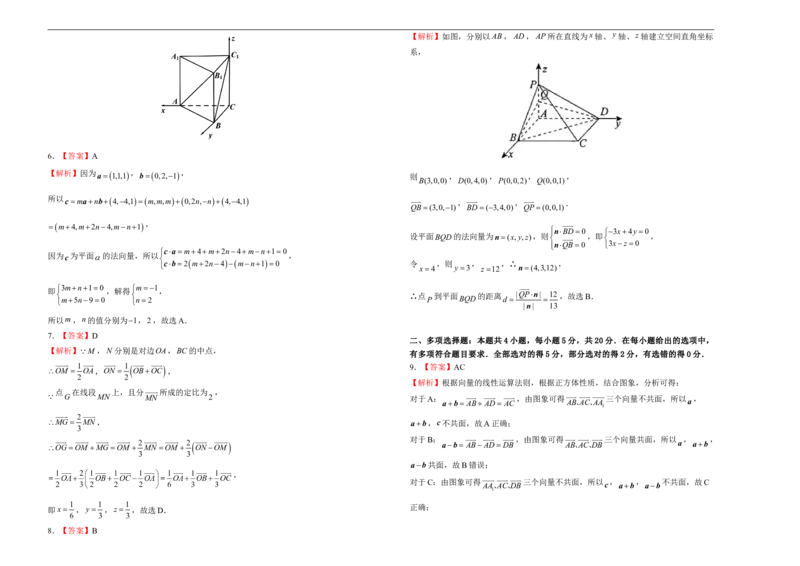
5．如图，在直三棱柱 中， ， ，则直线 与
ABCABC ACB90 CACC 2CB BC
1 1 1 1 1
1．已知空间向量
a
3,2,5， b1,x,1，且
a
与
b
垂直，则
x
等于（ ）
直线夹角的余弦值为（ ）
A．4 B．1 C．3 D．2 AB
1
2．设点 A4,2,1， O0,0,0，
M
1,1,2，若
O

M



A

B
，则点
B
的坐标为（ ）
A．1,3,3 B．1,3,3
C．5,1,1 D．5,1,1
3．如图，在长方体 中，下列各式运算结果为的有（ ）
ABCDABC D AC
1 1 1 1 1
A． 5 B． 5 C． 2 5 D．3
 
5 5 5 5
6．已知平面

内两向量
a
1,1,1， b0,2,1，若
c
为平面

的法向量且
封封密密不不订订装装只只卷卷此此
号号位位座座
号号场场考考
号号证证考考准准
名名姓姓
级级班班c
manb4,4,1，则
m
，
n
的值分别为（ ） 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，
有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．
A．1，2 B．1，2 C．1，2 D．1，2
9．在正方体
ABCDABC D
中，设
A

B

a
，
A

D

b
，
A

A

c
，a,b,c构成空间的
1 1 1 1 1
7．如图，已知空间四边形OABC，其对角线为OB，AC ，M ，N 分别是对边OA，
一个基底，则下列向量不共面的是（ ）
的中点，点 在线段 上，且分所成的定比为 ，现用基向量，，
BC G MN MN 2 OA OB
O  C 表示向量 O  G ，设 O  G   xO  A   yO  B  zO  C ，则 x ， y ， z 的值分别为（ ）
A．a，ab，c B．a，ab，ab
C．c，ab，ab D．c，abc，ab
10．直线 的方向向量为 ，两个平面 ， 的法向量分别为 ， ，则下列命题为真
l a   n m
命题的是（ ）
A．若a n，则直线l//平面
B．若a∥n，则直线l 平面
1 π
C．若cos a,n  ，则直线l与平面所成角的大小为
1 1 1 1 1 1 2 6
A．x ，y  ，z  B．x ，y  ，z 
3 3 3 3 3 6
D．若 3 ，则平面 ， 所成角的大小为π
1 1 1 1 1 1 cos m,n   
C．x ，y  ，z  D．x ，y  ，z  2 6
3 6 3 6 3 3
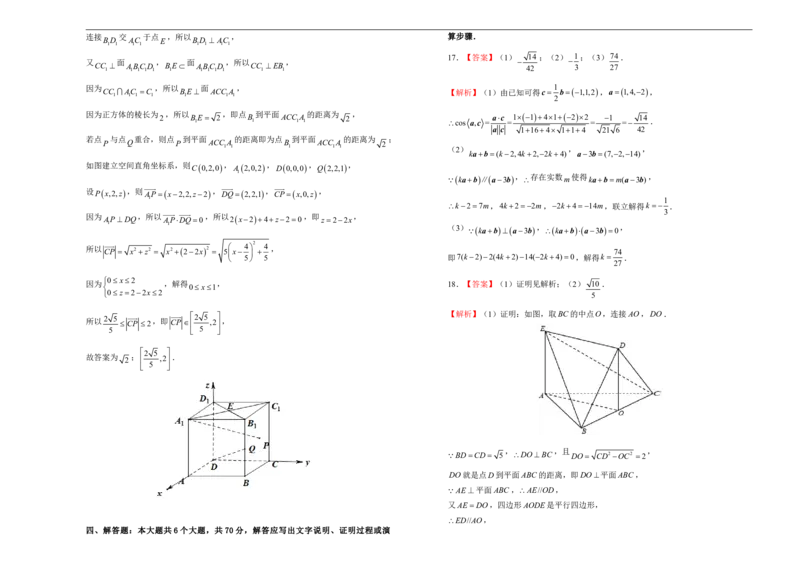
8．如图，点 为矩形 所在平面外一点， 平面 ， 为 的中点， 11．以下命题正确的是（ ）
P ABCD PA ABCD Q AP
A．若 p是平面的一个法向量，直线b上有不同的两点A，B，则b//的充要条件是
， ， ，则点 到平面 的距离为（ ）
AB3 BC 4 PA2 P BQD 
pAB0
 2 1 2
B．已知A，B，C三点不共线，对于空间任意一点O，若OP OA OB OC，
5 5 5
则P，A，B，C四点共面
25 4 3
C．已知a 1,1,2，b0,2,3，若  1与2ab垂直，则k 
 6 4
D．已知
△ABC
的顶点坐标分别为 A1,1,2， B4,1,4， C3,2,2，则
AC
边上的高
5 12 13 13
A． B． C． D．
13 13 5 12
的长为
BD 1312．如图，在正方体 中， 、 、 分别为 、 、 的中点， 为________．
ABCDABC D E F G BC CC BB
1 1 1 1 1 1
16．在棱长为2的正方体 中， 是棱 的中点，点 在侧面
ABCDABC D Q BB P BCC B
则（ ） 1 1 1 1 1 1 1
（包含边界）．
（1）若点 与点 重合，则点 到平面 的距离是________；
P Q P ACC A
1 1
（2）若 ，则线段 长度的取值范围是________．
AP  DQ CP
1
四、解答题：本大题共 6 个大题，共 70 分，解答应写出文字说明、证明过程或演
算步骤．
17．（10分）已知
a
1,4,2， b2,2,4．
1
（1）若c  b，求cosa,c的值；
2
（2）若kab∥a3b，求实数
k
的值；
（3）若kaba3b，求实数
k
的值．
A． B． 平面
DD AF AG// AEF
1 1
C．  A  C    A  B    A  A  0 D．向量 A  B 与向量 A  D 的夹角是 60
1 1 1 1 1 1
第Ⅱ卷
三、填空题：本大题共4小题，每小题5分．
13．已知空间直角坐标系中，点 A1,1,2， B3,0,4，若
c 6
，
c//

A

B
，则
c 
________．
14．在△ABC中， A1,2,1， B0,3,1， C2,2,1．若向量
n
与平面ABC垂直，
且
n  21
，则
n
的坐标为___________．
15．已知空间向量 满足 ， ，则 的值
a,b,c abc 0 a 3, b 1, c 4 abbcca
18．（12分）如图，在多面体ABCDE中，AE⊥平面ABC，点D到平面ABC的距离为 ， 是正三角形， ， ．
2 △ABC BDCD 5 AE  AB2
（1）证明：BC  DE ；
（2）求直线CE与平面BED所成角的正弦值．
19．（12分）如图，四棱锥PABCD的底面ABCD是菱形，BCD120，PA 底
面ABCD，PA AD2，E是AD的中点，F 为PD上一点，且PB∥平面CEF．
（1）求PF ；
20．（12分）如图所示，在等腰梯形ABCD中，AB∥CD，DAB60，AE∥CF ，
（2）求平面PAB与平面CEF所成角的正弦值． AE CF，CF 平面ABCD，DC  BC  ADCF 1．（1）求直线AD与平面ACM 的夹角余弦值；
（2）求平面ACD和平面ACM 的夹角的余弦值；
（3）求点P到平面ACM 的距离．
（1）求证：EF 平面BCF ；
（2）若M 为线段EF 上一点，且FM EF ，是否存在实数，使平面MAB与平面

ABC所成锐二面角为 ？若存在，求出实数；若不存在，请说明理由．
3
22．（12分）已知正方形的边长为4，E，F分别为AD，BC的中点，以EF为棱将正
21．（12分）如图，在四棱锥PABCD中，底面ABCD是矩形，PA 平面ABCD，
方形ABCD折成如图所示的60°的二面角，点M在线段AB上．
PA AD4，AB2，M 是PD中点．（1）若M为AB的中点，且直线MF与由A，D，E三点所确定平面的交点为O，试确
定点O的位置，并证明直线OD∥平面EMC；
（2）是否存在点M，使得直线DE与平面EMC所成的角为60°；若存在，求此时二面
角M－EC－F的余弦值；若不存在，说明理由．（新教材）2021-2022 学年上学期高二
第一次月考备考金卷
数 学 （A） 答 案
第Ⅰ卷
一、单项选择题：本题共8小题，每小题 5分，共40分．在每小题给出的四个选项
中，只有一项是符合题目要求的．
1．【答案】A
则
A

B
 1,0,0，
A

D
 0,1,0，
A

E
 0,0,1，
【解析】由于a与b垂直，所以32x50 x4，故选A．
2．【答案】C  3 1 2
因为AP  AB AD AE ，
4 2 3
【解析】设点B的坐标为 ，则 ， ，
(x,y,z) OM (1,1,2) AB(x4,y2,z1)
 
 3 1 2 APAB 3  3 2 1 2 2 2 181
所以AP  , , ，   ， AP           ，
x41 x5 4 2 3 AB 4 4 2 3 144
∵ O  M    A  B ，∴  y21，解得  y 1，故选C．
  z12   z 1   A  P    A  B   2
所以点P到AB的距离 d   A  P 2    181  9  5，故选C．

3．【答案】D  AB  144 16 6
 
【解析】①
A

B



B

C

C

C



A

C

C

C



A

C

； 5．【答案】A
1 1 1
【解析】以 为原点， ， ， 分别为 ， ， 轴建系，如图所示：
②
A

B



B

C



D

D



A

C

C

C



A

C

；
C CA CB CC
1
x y z
1 1 1
③
A

B



A

D

C

C



A

B



B

C

C

C



A

C

；
设
CACC
1
2CB 2
，则 A2,0,0， B0,1,0，
B
1
0,1,2，
C
1
0,0,2，
1 1 1
④
A

B



A

D



D

D



A

B



B

C

C

C



A

C

；
所以
A

B

1
2,1,2，
B

C

1
0,1,2，
1 1 1
设直线 与 直线夹角为 ，
⑤
A

B



A

A



A

D



A

B



B

B



B

C



A

C

；
BC
1
AB
1

1 1 1 1 1 1 1
 
AB BC
⑥
A

B



A

D



A

A

1


A

C

C

C

1


A

C

1
， 则cos

1

1


3

5
，故选A．
AB  BC 414 14 5
1 1
所以①②③④⑤⑥都正确，故选D．
4．【答案】C
【解析】如图，以A为坐标原点，AB，AD，AE所在直线分别为x，y，z轴建立空间直
角坐标系，【解析】如图，分别以AB，AD，AP所在直线为x轴、y轴、z 轴建立空间直角坐标
系，
6．【答案】A
【解析】因为
a
1,1,1， b0,2,1，
则 ， ， ， ，
B(3,0,0) D(0,4,0) P(0,0,2) Q(0,0,1)
所以 c manb4,4,1m,m,m0,2n,n4,4,1  ， ， ．
QB(3,0,1) BD(3,4,0) QP(0,0,1)
m4,m2n4,mn1，

 nBD0 3x4y 0
设平面BQD的法向量为n(x,y,z)，则

，即

，

nQB0 3xz 0
ca m4m2n4mn10
因为c为平面的法向量，所以

，
cb2m2n4mn10 令 ，则 ， ，∴ ，
 x4 y 3 z 12 n(4,3,12)
即
3mn10
，解得
m1
， 
  ∴点 到平面 的距离 |QPn| 12 ，故选B．
m5n90 n2 P BQD d  
|n| 13
所以m，n的值分别为1，2，故选A．
7．【答案】D
二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，
【解析】 M ，N 分别是对边OA，BC的中点，
 有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．
 1  1  9．【答案】AC
OM  OA，ON  OBOC ，
2 2
【解析】根据向量的线性运算法则，根据正方体性质，结合图象，分析可得：
点 在线段 上，且分所成的定比为 ，
 G MN MN 2 对于A：   ，由图象可得  三个向量不共面，所以 ，
ab AB AD AC AB、AC、AA a
1
 2
MG  MN， ab，c不共面，故A正确；
3
    2  2  对于B： ab  A  B    A  D    D  B ，由图象可得 A  B  、  A  C  、  D  B 三个向量共面，所以 a ， ab ，
OG OM MG OM  MN OM  ON OM
3 3
ab共面，故B错误；
，
对于C：由图象可得  三个向量不共面，所以 ， ， 不共面，故C
AA、AC、DB c ab ab
1
1 1 1
正确；
即x ，y  ，z  ，故选D．
6 3 3
8．【答案】B对于D：    ，由图象可得  共面，所以 ，
abc  AB AD AA  AC AA、AC、AC c 所以 边上的高  13 ，故D正确，
1 1 1 1 AC BD  AB sinA 29  13
29
abc，ab共面，故D错误，
故选BCD．
故选AC．
12．【答案】BC
10．【答案】BC
【解析】以点 为坐标原点， 、 、 所在直线分别为 、 、 轴建立如下
【解析】对于A：若a n，则直线l//平面或在平面内，故选项A不正确； D DA DC DD x y z
1
对于B：若a∥n，则a也是平面的一个法向量，所以直线l 平面，故选项B正确；
图所示的空间直角坐标系，
对于C：直线与平面夹角的正弦值等于直线与平面法向量夹角的余弦值的绝对值，所
设正方体
ABCDABC D
的棱长为
2
，则 A2,0,0、 B2,2,0、 C0,2,0、 D0,0,0、
1 1 1 1
1 π
以若cos a,n  ，则直线l与平面所成角的大小为 ，故选项C正确；
2 6
E1,2,0、 F0,2,1、 G2,2,1、
A
2,0,2、
B
2,2,2、
C
0,2,2、
D
0,0,2．
1 1 1 1
对于D：两个平面所成角与他们法向量所成的角相等或互补，若 3 ，则平
cos m,n 
2 对于A选项，
D

D
 0,0,2，
A

F
 2,2,1，则
D

D



A

F

20
，故A选项错误；
1 1
面，所成角的大小为
π
或
5π
，故选项D不正确，
对于B选项，设平面
AEF
的法向量为
m
x,y,z，
A

E
 1,2,0，
E

F
 1,0,1，
6 6
故选BC．
  x
由  mAE x2y 0 ，可得y  ，取 ，可得 ， ，
11．【答案】BCD   2 x2 m 2,1,2 AG 0,2,1
 1
mEF xz 0  z  x
【解析】对于A，若直线 ，则  成立，故 不是  的必要条件，
b pAB0 b// pAB0
 ， ，
mAG 220 m  AG
故A错误；  1 1
 2 1 2 2  1  2  平面 ， 平面 ，故B选项正确；
对于B，若OP OA OB OC，则 OPOA  OBOP  OCOP ，  A 1 G AEF A 1 G// AEF
5 5 5 5 5 5
 1 
所以AP PBPC ，所以P，A，B，C四点共面，故B正确；
2
对于C，由题意可得 kabk,k2,2k3， 2ab2,0,1，
25 4 3
若  1与2ab垂直，则 kab2ab2k2k30，解得k  ，
 6 4
故C正确；
对于D，由题意
A

B
 5,0,2，
A

C
 4,3,0，
 
ACAB 20 4 29

则 AB  254  29，cosA     ，
AC  AB 5 29 29
所以 13 ，
sin A 1cos2 A 
29∵
c//

A

B
，∴存在

，使得
c 

A

B
 2,,2R，
∴
c 
22 2 22
36
，解得2，
∴
c
4,2,4或4,2,4，
故答案为4,2,4或4,2,4．
14．【答案】 或
(2,4,1) (2,4,1)
【解析】据题意，得 ， ．
AB(1,1,2) AC (1,0,2)
设 ，∵ 与平面ABC垂直，
n(x,y,z) n
 y
 x
 nAB0 ，即 x y2z 0 ，可得   2 ，
  

nAC 0 x2z 0 
z 
y
 4
对于C选项，

A

B

1 0,2,2，

A

1

C

2,2,2，

A

1

C



A

1

B

1 

A

1

A



A

B

1 

A

1

C

440，  n  21 ，  x2  y2 z2  21 ，解得 y 4 或 y 4 ．
故C选项正确； 当 时， ， ；当 时， ， ，
y 4 x2 z 1 y 4 x2 z 1
对于D选项，
A

B
 0,2,2，
A

D
 2,0,2，
1 1 ∴ 的坐标为 或 ，
n (2,4,1) (2,4,1)
  故答案为 或 ．
  ABAD 4 1 (2,4,1) (2,4,1)
cos AB,AD  1 1   ，
1 1  A  B    A  D  2 22 2 2
1 1
15．【答案】13
所以，向量与向量的夹角是 ，故D选项错误，
A 1 B AD 1 120 【解析】因为 abc 0 ，所以abc2 0 ，则 a2 b2 c2 2abbcca0 ，
故选BC．
因此 32 12 42 ，故答案为 ．
abbcca  13 13
2
第Ⅱ卷
2 5 
16．【答案】 2 ，  ,2
三、填空题：本大题共4小题，每小题5分．  5 
13．【答案】4,2,4或4,2,4
【解析】在正方体 中， ， 面 ， 面
ABCDABC D BB //CC BB  ACC A CC 
1 1 1 1 1 1 1 1 1 1
【解析】∵ A1,1,2， B3,0,4，∴
A

B
 2,1,2，
，所以 面 ，
ACC A BB // ACC A
1 1 1 1 1连接 交 于点 ，所以 ， 算步骤．
BD AC E BD  AC
1 1 1 1 1 1 1 1
17．【答案】（1） 14 ；（2） 1；（3）74 ．
又 面 ， 面 ，所以 ，  
CC  ABC D BE  ABC D CC  EB 42 3 27
1 1 1 1 1 1 1 1 1 1 1 1
因为 ，所以 面 ， 1
CC
1
A
1
C
1
C
1
B
1
E  ACC
1
A
1
【解析】（1）由已知可得c  b1,1,2，a 1,4,2，
2
因为正方体的棱长为 2 ，所以 BE  2 ，即点 B 到平面 ACC A 的距离为 2 ， ac 114122 1 14
1 1 1 1 cos a,c = = = = ．
a c 1164 114 21 6 42
若点 与点 重合，则点 到平面 的距离即为点 到平面 的距离为 ；
P Q P ACC A B ACC A 2
1 1 1 1 1 （2） ， ，
kab(k2,4k2,2k4) a3b(7,2,14)
如图建立空间直角坐标系，则 C0,2,0，
A
2,0,2， D0,0,0， Q2,2,1，
1
kab∥a3b，

存在实数
m
使得
kabm(a3b)
，

设 Px,2,z，则
A

P
 x2,2,z2，
D

Q
 2,2,1，
C

P
 x,0,z，
1 1
k27m，4k22m，2k414m，联立解得k  ．
3
因为 AP  DQ ，所以 A  P    D  Q  0 ，所以 2x24z20 ，即 z 22x ，
1 1
（3） kaba3b， kaba3b0 ，

2
所以 C  P   x2 z2  x2 22x2  5   x 4   4 ， 74
 5 5 即7(k2)2(4k2)14(2k4)0，解得k  ．
27
0 x2
因为 ，解得 ， 18．【答案】（1）证明见解析；（2） 10 ．
 0 x1
0 z 22x2
5
所以 2 5  C  P  2 ，即 C  P     2 5 ,2   ，
【解析】（1）证明：如图，取BC的中点O，连接AO，DO．
5  5 
2 5 
故答案为 2 ；  ,2 ．
5
 
， ，且 ，
BDCD 5 DO BC DO CD2 OC2 2

DO就是点D到平面ABC的距离，即DO平面ABC，
AE⊥平面ABC，AE//OD，

又AE  DO，四边形AODE是平行四边形，
ED//AO，
四、解答题：本大题共 6 个大题，共 70 分，解答应写出文字说明、证明过程或演△ABC是正三角形，AO BC，BC  DE．

从而 ，故 4 2 ．
PD PA2  AD2 2 2 PF 
（2）解：由（1）得AO平面BCD，
3
以 为 轴的正方向建立如图所示的空间直角坐标系 ，
OB x Oxyz （2）以A为原点，AD，AP所在的直线分别为y轴，z 轴，建立如图所示的空间直角
坐标系 ，
Axyz
则B1,0,0，C1,0,0，E  0, 3,2 ，D0,0,2，
则 ， ， ， ， ，  4 2，
A(0,0,0) B( 3,1,0) P(0,0,2) C( 3,1,0) E(0,1,0) F  0, , 
 3 3
设平面
BED
的法向量为 nx,y,z，
B

D
 1,0,2，
 ， ， ，  1 2，

B

E



1, 3,2
，C 
E



1, 3,2
， AB( 3,1,0) AP(0,0,2) CE ( 3,0,0) CF  

 3,
3
,
3



则由    BDn0 ，得   x2z 0 ，令x2，得n2,0,1， 设平面 PAB 的一个法向量为 m x 1 ,y 1 ,z 1 ，

BEn0 x 3y2z 0

 ABm 0  3x  y 0
设直线CE与平面BED所成角为， 由  ，即  1 1 ，取x 1，则m (1, 3,0)；
 1

APm 0  2z
1
0
CEn
 4 10
则sin cos CE,n    ，
C  E  n 2 2 5 5 设平面 CEF 的一个法向量为 nx ,y ,z ，
2 2 2
故直线 与平面 所成角的正弦值 10 ．   3x 0
CE BED  CEn0  2
5
由
 
，即
 1 2
，取y
2
2，则n(0,2,1)，
CFn0  3x  y  z 0
 2 3 2 3 2
19．【答案】（1） 4 2 ；（2） 10 ．
PF 
3 5 所以 mn 2 3 15 ，所以 10 ，
cosm,n    sin m,n 
|m||n| 2 5 5 5
【解析】（1）连接BD交CE于M ，连接MF，
因为PB∥平面CEF，PB平面PBD，平面PBD  平面CEF MF ，所以PB∥MF ． 故平面 与平面 所成角的正弦值为 10 ．
PAB CEF
DM DE 1 5
由△BCM △DEM ，得   ，

MB BC 2
1
20．【答案】（1）证明见解析；（2）存在， ．
DF DM DF 1 2
3
又  ，所以  ，即PF  PD，
FP MB FP 2 3
【解析】（1）因为AE∥CF ，AE CF，
因为PA平面ABCD，AD平面ABCD，所以PA AD，所以四边形ACFE为平行四边形，所以AC∥EF ．
21．【答案】（1） 30 ；（2） 6 ；（3）2 6 ．
在等腰梯形ABCD中，DAB60，DC  BC CF  AD1，
6 6 3
所以AB2BC，所以AC  BC ．
【解析】因为 平面 ，且四边形 是矩形，所以 两两垂直，
PA ABCD ABCD AB,AD,AP
又CF 平面ABCD，所以AC CF，BC CF C ，BC，CF 平面BCF，

所以AC 平面BCF． 所以分别以 所在的直线为 轴建立如图所示空间直角坐标系，
AB,AD,AP x,y,z
因为AC//EF ，所以EF 平面BCF．
（2）依题意，以C为坐标原点，分别以直线 为x轴、y轴、z轴建立如图所
CA,CB,CF
示的空间直角坐标系，
所以C(0,0,0)，A  3,0,0 ，B0,1,0，
设 ，所以 ， ，
M( 3,0,1) AB( 3,1,0) BM ( 3,1,1)
（1） A0,0,0，
D(0,4,0)
，
C(2,4,0)
， P0,0,4，
M
0,2,2，
设
n
x,y,z为平面MAB的法向量，
1
所以 ， ， ，
AD(0,4,0) AC (2,4,0) AM (0,2,2)

 n AB0   3x y 0
由   n 1   B  M  0 ，得   3x yz 0 ，取x1，所以n 1 (1, 3, 3 3)， 设平面 ACM 的法向量为 m x,y,z，
1
因为
n
0,0,1是平面ABC的一个法向量，
 

A

C

m 0 2x4y 0
2 由
 
，可得

，取y 1，则z 1，x2，
AM m 0 2y2z 0
设平面MAB与平面ABC所成的锐二面角为，
所以
m
2,1,1，
n n 3 3 1
所以cos 1 2   ．
n 1  n 2 13  3 3 2 2 记直线AD和平面ACM 的夹角为，

ADm
 4 6 30
因为 01 ，所以  1，所以 FM  3 ，
则sincos AD,m 
 A  D   m

4 6

6
，所以cos 1sin2
6
．
3 3
（2）由图可知，平面 即 平面，所以平面 的法向量为 ，
ACD xoy xoy n(0,0,1)
所以存在 FM 1 使平面MAB与平面ABC所成锐二面角为．
 
EF 3 3
mn 1 6
记面
ACD
和面
ACM
的夹角为，则
cos m,n   
，
m n 61 6由图可知面 和面 夹角为锐角，所以 6 ．
ACD ACM cos
6
（3） P0,0,4，
A

P
 0,0,4，平面
ACM
的法向量为
m
2,1,1，

设点 到平面 的距离为 ，则 APm 4 2 6 ，
P ACM d d   
|m| 6 3
所以点 到平面 的距离为2 6 ．
P ACM
3
22．【答案】（1）点O在EA的延长线上，且AO2，证明见解析；（2）存在，
所以E1,0,0，D  0,0, 3 ， C(0,4, 3) ，F1,4,0，
1 1
cos 或 ．
4 4 所以  E  D    1,0, 3 ，  E  C    1,4, 3 ，
【解析】（1）证明：因为直线MF 平面ABFE，故点O在平面ABFE内也在平面
ADE内，
设
M
1,t,0(0≤t≤4)，则
E

M
 2,t,0，
所以点O在平面ABFE与平面ADE的交线上(如图所示)．

 mEM 0  2xty 0
设平面EMC的法向量m x,y,z，则

，所以

，

mEC 0 x4y 3z 0
8t  8t
取 ，则 ， ，所以 ．
y 2 xt z  m  t,2,
 
3  3 
8 3

因为DE与平面EMC所成的角为60°，所以 8t2 2 ，
2 t2 4
3
所以 ，解得 或 ，
t2 4t30 t 1 t 3
所以存在点M，使得直线DE与平面EMC所成的角为60°．
因为AO∥BF，M为AB的中点，所以△OAM≌△FBM，所以OM=MF，AO=BF，
取ED的中点Q，则为平面CEF的法向量．
所以点O在EA的延长线上，且AO=2． QA
连接DF交EC于N，
 1 3  3 3  8t
因为四边形CDEF为矩形，所以N是EC的中点． 因为点Q的坐标为    ,0,   ，所以QA  ,0,   ，m   t,2,  ，
 2 2   2 2   3 
连接MN，所以MN为△DOF的中位线，所以MN∥OD，
设二面角M BCF的大小为，
又因为MN 平面EMC，所以直线OD∥平面EMC．
（2）存在．由已知可得，EF⊥AE，EF⊥DE，所以EF⊥平面ADE，
所以平面ABFE⊥平面ADE．
取AE的中点H为坐标原点，建立如图所示的空间直角坐标系，维权 声明

QAm 2t4 t2
所以 cos    ，
QA m 8t 2 t2 4t19
3 t2 4
 
 3 
因为当t=2时，cos0，此时平面EMC⊥平面CDEF，
1
所以当t=1时，为钝角，所以cos ；
4
1
当t=3时，为锐角，所以cos ．
4