数学答案_2024年5月_01按日期_1号_2024届湖南省岳阳市高三教学质量监测（三）_2024届湖南省岳阳市高三下学期三模数学试题

岳阳市 届高三教学质量监测（三） 2024 数学参考答案及评分标准 一、选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一 项是符合题目要求的．) 1.B 2.C 3.A 4.B 5.D 6.D 7.B 8.C 二、选择题(本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合 题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．) 9.BD 10.ABD 11.ABD 三、填空题(本大题共3小题，每小题5分，共15分．) 5 12. 2 5    13. ； （答案不唯一，符合 k,且 2k,kZ 即可） 12 12 12 2 6 14. 3 四、解答题(本大题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．) 15.（本小题满分13分） 已知等差数列{a }满足：a 2，且a 、a 、a 成等比数列． n 1 1 2 4 (1)求数列{a }的通项公式； n 4n2 (2)若等差数列{a }的公差不为零且数列{b }满足：b  ，求数列{b }的 n n n (a 1)(a 1) n n n 前n项和T . n 解析：设数列  a  的公差为d ，依题意，2，2d,23d成等比数列，---------------------1分 n 所以（2d）2 （2 23d），解得d 0或d 2，---------------------3分 当d 0时，a 2；---------------------4分 n 当d 2时，a 2(n1)22n---------------------5分 n   所以数列 a 的通项公式为a 2或a 2n---------------------6分 n n n (2)因为等差数列{a }的公差不为零，由(1)知a 2n(nN*)， n n 4n2 4n2 则b   ---------------------7分 n (a 1)(a 1) (2n1)(2n1) n n {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}4n2 11 1 1 1 所以b  1 (  )---------------------10分 n (2n1)(2n1) 2 2n1 2n1 1 1 1 1 1 1 1 1 1 1 1 1 所以T [1 (  )][1 (  )][1 (  )][1 (  )] n 2 1 3 2 3 5 2 5 7 2 2n1 2n1 1 1 1 n T n (  )n ---------------------13分 n 2 1 2n1 2n1 16.（本小题满分15分） 某地区举行专业技能考试，共有8000人参加，分为初试和复试，初试通过后，才能参 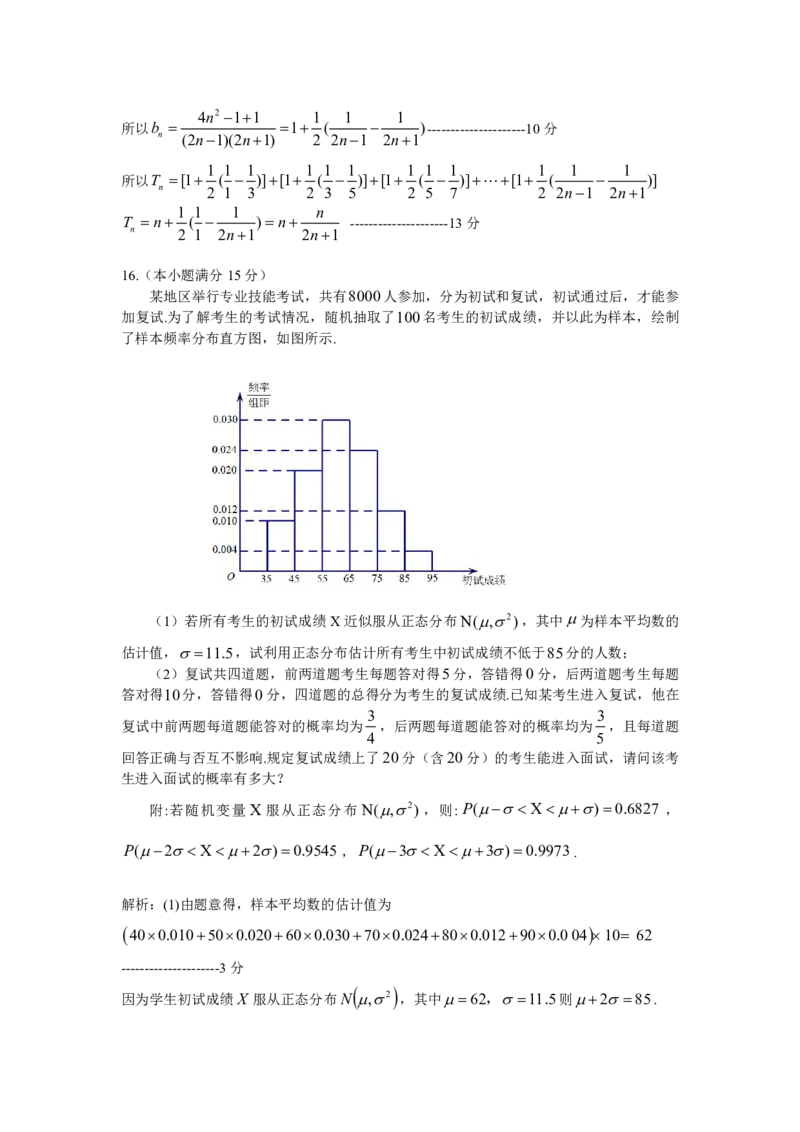加复试.为了解考生的考试情况，随机抽取了100名考生的初试成绩，并以此为样本，绘制 了样本频率分布直方图，如图所示. （1）若所有考生的初试成绩X近似服从正态分布N(,2)，其中为样本平均数的 估计值，11.5，试利用正态分布估计所有考生中初试成绩不低于85分的人数； （2）复试共四道题，前两道题考生每题答对得5分，答错得0分，后两道题考生每题 答对得10分，答错得0分，四道题的总得分为考生的复试成绩.已知某考生进入复试，他在 3 3 复试中前两题每道题能答对的概率均为 ，后两题每道题能答对的概率均为 ，且每道题 4 5 回答正确与否互不影响.规定复试成绩上了20分（含20分）的考生能进入面试，请问该考 生进入面试的概率有多大？ 附:若随机变量  服从正态分布 N(,2) ，则: P()0.6827 ， P(22)0.9545 ，P(33)0.9973. 解析：(1)由题意得，样本平均数的估计值为  400.010500.020600.030700.024800.012900.004 10 62 ---------------------3分   因为学生初试成绩X 服从正态分布N ,2 ，其中62，11.5则285. {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}---------------------5分 10.9545 所以P(X 85) P(X 2) 0.02275---------------------7分 2 所以估计初试成绩不低于85分的人数为0.022758000182人---------------------8分 （2）记该考生的复试成绩为Y ，则能进入面试的复试成绩为 20 分，25 分，30 分 ---------------------9分 1 3 3 3 2 117 P(Y 20)( )2( )2 ( )2C1   ---------------------10分 4 5 4 2 5 5 400 3 1 3 54 P(Y 25)C1  （ ）2  ---------------------12分 2 4 4 5 400 3 3 81 P(Y 30)( )2（ ）2  ---------------------14分 4 5 400 所以该考生进入面试的概率为 117 54 81 63 P(Y 20)P(Y 25)P(Y 30)    ---------------------15分 400 400 400 100 17.（本小题满分15分） 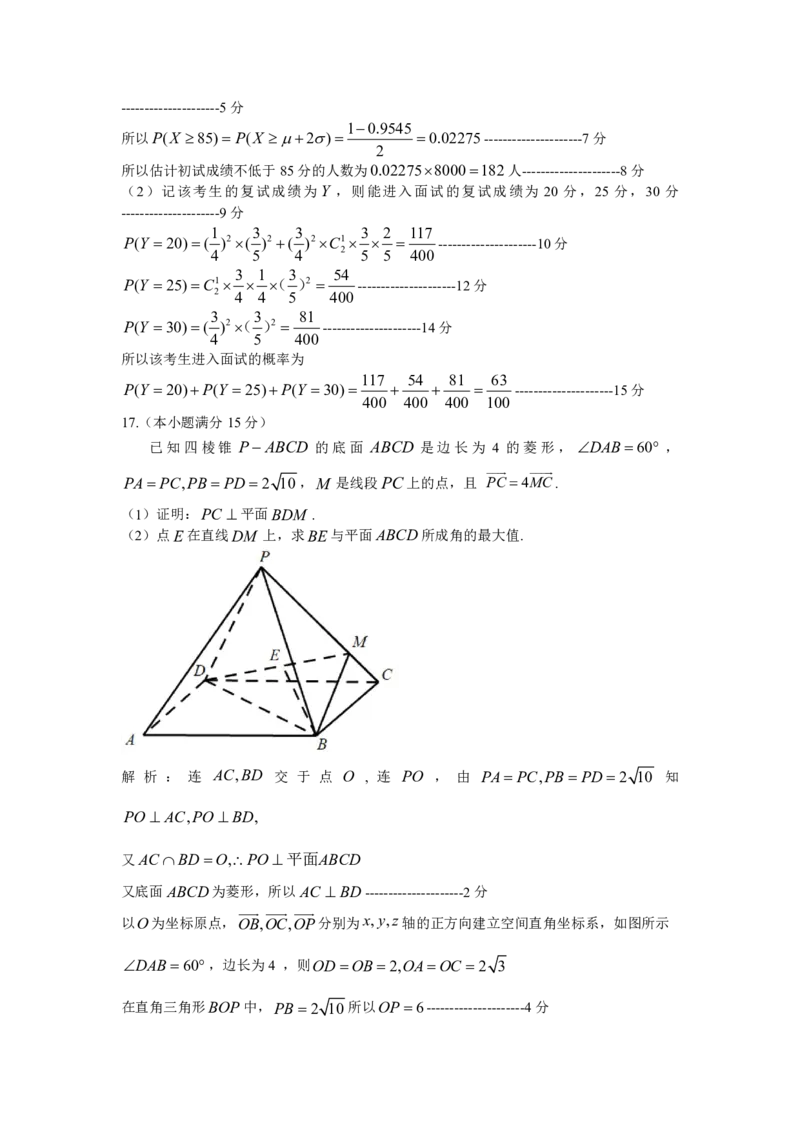已知四棱锥 P ABCD 的底面 ABCD 是边长为 4 的菱形， DAB60 ，   PA PC,PB  PD 2 10 ，M 是线段PC上的点，且 PC 4MC. （1）证明：PC 平面BDM . （2）点E在直线DM 上，求BE与平面ABCD所成角的最大值. 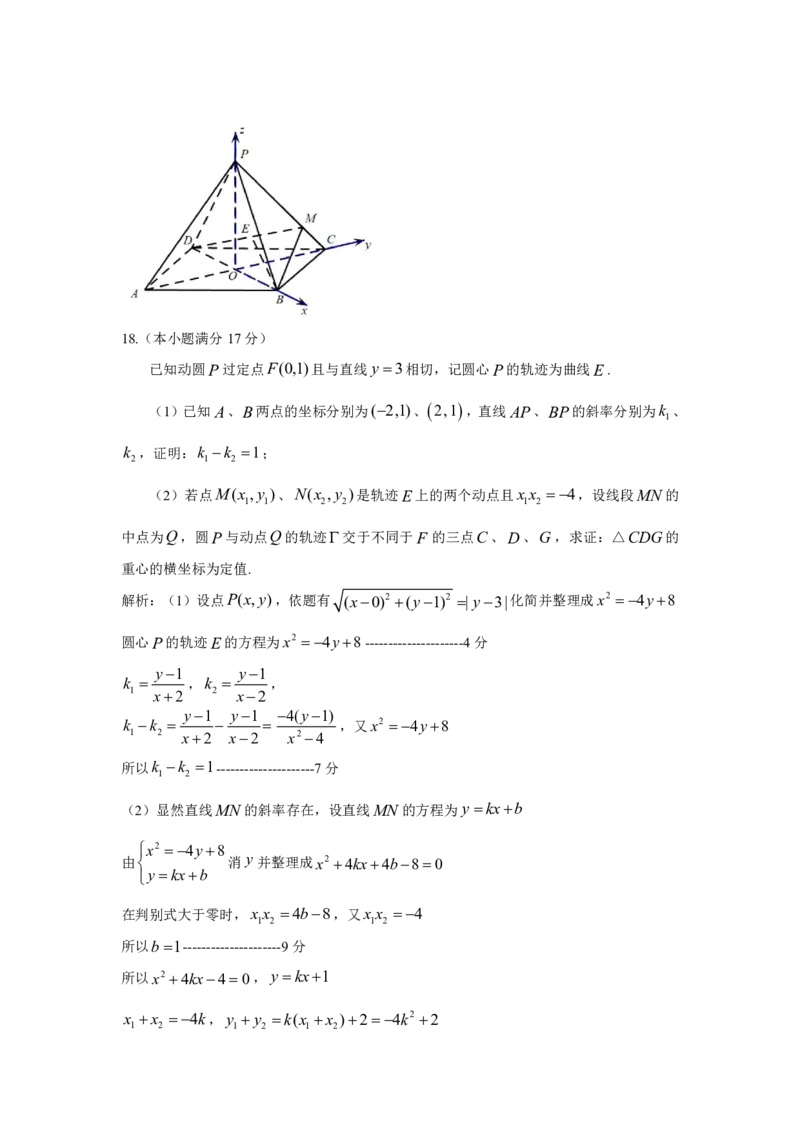解 析 ： 连 AC,BD 交 于 点 O , 连 PO ， 由 PA PC,PB  PD 2 10 知 PO  AC,PO BD, 又ACBD O,PO 平面ABCD 又底面ABCD为菱形，所以AC BD---------------------2分    以O为坐标原点，OB,OC,OP分别为x,y,z轴的正方向建立空间直角坐标系，如图所示 DAB60，边长为4 ，则OD OB  2,OAOC  2 3 在直角三角形BOP中，PB 2 10 所以OP 6---------------------4分 {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}所以点O(0,0,0),P(0,0,6),B(2,0,0),D(2,0,0),C(0,2 3,0)   3 3 3 PC 4MC ，则 M(0, , ) 2 2   3 3 3  3 3 3 所以PC (0,2 3,6),DM (2, , ),BM (2, , ), 2 2 2 2   3 3 3 所以PCDM 022 3 (6) 0, 2 2   3 3 3 PCBM 0(2)2 3 (6) 0,---------------------6分 2 2     所以PC DM,PC BM 所以PC DM,PC BM 又DM BM M 所以PC 平面BDM ---------------------8分 （2）设DE DM ， 3 3 3  3 3 3 则E(22, , )，所以BE (24, , ) 2 2 2 2  平面ABCD的一个法向量是n(0,0,1)，设BE与平面ABCD所成角为，则 3 3 || || |BEn| 2 2 sin|cos BE,n|   |BE||n| 3 3 3 132 1616 (24)2 ( )2 ( )2 2 2 ---------------------11分 当0时，BE 平面ABCD，0； 当0时， 3 || 3 3 1 2 sin    -----------------13 132 1616 16 16 1 1 2 2 13  2 16（  ）2 9  2  2 分    又[0, ]所以 ，故BE与平面ABCD所成角的最大值为 ---------------------15分 2 6 6 {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}18.（本小题满分17分） 已知动圆P过定点F(0,1)且与直线 y3相切，记圆心P的轨迹为曲线E. （1）已知A、B两点的坐标分别为(2,1)、  2,1  ，直线AP、BP的斜率分别为k 、 1 k ，证明：k k 1； 2 1 2 （2）若点M(x ,y )、N(x ,y )是轨迹E上的两个动点且x x 4，设线段MN的 1 1 2 2 1 2 中点为Q，圆P与动点Q的轨迹交于不同于F 的三点C、D、G，求证：△CDG的 重心的横坐标为定值. 解析：（1）设点P(x,y)，依题有 (x0)2 (y1)2 | y3|化简并整理成x2 4y8 圆心P的轨迹E的方程为x2 4y8---------------------4分 y1 y1 k  ，k  ， 1 x2 2 x2 y1 y1 4(y1) k k    ，又x2 4y8 1 2 x2 x2 x24 所以k k 1---------------------7分 1 2 （2）显然直线MN的斜率存在，设直线MN的方程为 ykxb x2 4y8 由 消 y并整理成x2 4kx4b80 y kxb 在判别式大于零时，x x 4b8，又x x 4 1 2 1 2 所以b1---------------------9分 所以x2 4kx40，ykx1 x x 4k，y  y k(x x )24k2 2 1 2 1 2 1 2 {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}所以线段MN的中点坐标为Q(2k,2k2 1)---------------------10分 x2k 设Q(x,y)，则 消k得x2 2y2 y2k2 1 所以Q的轨迹方程是x2 2y2---------------------11分 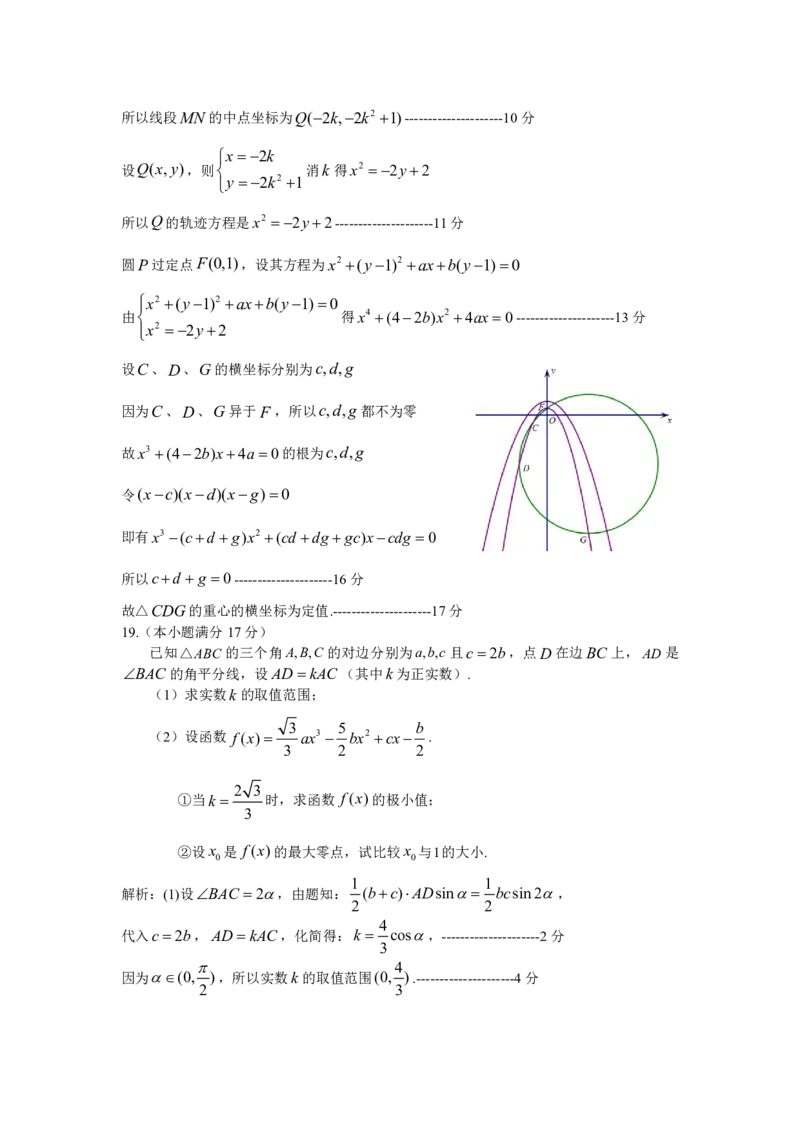圆P过定点F(0,1)，设其方程为x2 (y1)2 axb(y1)0 x2 (y1)2 axb(y1)0 由 得x4 (42b)x2 4ax 0---------------------13分 x2 2y2 设C、D、G的横坐标分别为c,d,g 因为C、D、G异于F ，所以c,d,g都不为零 故x3 (42b)x4a 0的根为c,d,g 令(xc)(xd)(xg)0 即有x3 (cd g)x2 (cd dggc)xcdg 0 所以cd g 0---------------------16分 故△CDG的重心的横坐标为定值.---------------------17分 19.（本小题满分17分） 已知△ABC 的三个角A,B,C 的对边分别为a,b,c且c2b，点D在边BC上，AD是 BAC的角平分线，设AD kAC（其中k为正实数）. （1）求实数k 的取值范围； 3 5 b （2）设函数 f(x) ax3  bx2 cx . 3 2 2 2 3 ①当k  时，求函数 f(x)的极小值； 3 ②设x 是 f(x)的最大零点，试比较x 与1的大小. 0 0 1 1 解析：(1)设BAC 2，由题知： (bc)ADsin bcsin2， 2 2 4 代入c2b，AD kAC，化简得：k  cos，---------------------2分 3  4 因为(0, )，所以实数k的取值范围(0, ).---------------------4分 2 3 {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}2a a 法二：c2b及由角平分线性质知BD  ,DC  3 3 在△ABD和△ADC中由余弦定理得 AB2 BD2 AD2 2BDADcosADB,AC2 CD2 AD2 2CDADcosADC 所以 2a 2a a a c2 ( )2 (kb)2 2 kbcosADB,b2 ( )2 (kb)2 2 kbcosADC 3 3 3 3 又ADBADC  π，则cosADBcosADC 0 2a2 2a2 所以c2 2b2  3(kb)2 ,又c2b，所以(63k2)b2  ---------------------2分 3 3 b2ba 在△ABC 中有 ， ab2b a 3(63k2) 所以1 3，所以1 9 b 2 4 4 得0k  ，所以实数k的取值范围(0, )---------------------4分 3 3 2 3 3   （2）①当k  时，由(1)知cos ，则 此时BAC  ， 3 2 6 3  由余弦定理有：a2 b2 c2 2bccos 及c2b得a  3b，--------------------5分 3 2a2 2 3 法二：由(63k2)b2  ，当k  时有a  3b--------------------5分） 3 3 5 1 故 f(x)b(x3 x22x )， f '(x)b(3x25x2)b(3x2)(x1) ------------6分 2 2 2 由 f '(x)0得x 或x1 3 2 由 f '(x)0得  x1 3 2 2 故 f(x)在(, )，(1,)上单调递增，在( ,1)上单调递减， 3 3 故 f(x)的极小值为 f(1)0.---------------------9分 2 3 ②（i）当k  时，由①知a  3b，又c2b， 3 5 1 b 故 f(x)b(x3 x22x ) (x1)2(2x1) 2 2 2 {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}1 知 f(x)的零点为1, 故 f(x)的最大零点x 1；---------------------10分 0 2 2 3 3 1 （ii）当k  时，由(1)知cos ，则cosBAC 2cos21 ， 3 2 2 b2 c2 a2 1 由余弦定理有cosBAC   ，代入c2b， 2bc 2 解得a 3b， 由abc知a cbb，故a(b, 3b)， a 5 1 3a 3a f(x)b( x3  x2 2x )， f'(x)b( x2 5x2)，设t  ( 3,3) 3b 2 2 b b 5 258t 5 258t 令 f'(x)0解得：x  ，x  ，且x  x 1 2t 2 2t 1 2 则 f(x)在(,x )，(x ,)上单调递增，(x ,x )上单调递减， 1 2 1 2 因为 f'(1)b(t3)0，故x 1 x ， 1 2 t 且 f(1)b( 1)0，x时， f(x)0，故 f(x)在(1,)上有唯一零点x ， 0 3 此时x 1成立；---------------------13分 0 2 3 3 1 (iii)k  时，由(1)知0cos ，则cosBAC 2cos21(1, )， 3 2 2 b2 c2 a2 由余弦定理有cosBAC  ，及c2b，解得 3ba3b， 2bc 由abc知a cbb， 故 3ba3b， 所以t(3,3 3) 25 5 258t 5 258t 当t(3, )时，令 f'(x)0解得：x  ，x  ，且x  x 8 1 2t 2 2t 1 2 由（ii）知则 f(x)在(,x )，(x ,)上单调递增，(x ,x )上单调递减， 1 2 1 2 5 因为 f'(1)b(t3)0，且 f '(x)b(tx25x2) 的图象的对称轴x 1 2t {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}t 所以x  x 1，又因为 f(1)b( 1)0，故 f(x)在(1,)上无零点， 1 2 3 b 且 f(0) 0，故x (0,1)，x 1成立；---------------------15分 0 0 2 25 t 当t[ ，3 3)时， f'(x)0恒成立，则 f(x)在R上单调递增，由 f(1)b( 1)0， 8 3 b f(0) 0知x 1成立；---------------------16分 0 2 2 3 2 3 2 3 4 综上，当0k  时x 1；当k  时x 1；当 k  时x 1.----------17 3 0 3 0 3 3 0 分 {#{QQABDYAEggiAApAAABgCAQ2iCkEQkBEAAAoGRBAEsAAAyRFABCA=}#}