数学答案·2024年高考最后一卷_2024年5月_01按日期_21号_2024届安徽皖江名校联盟高三5月最后一卷G-024_皖江名校联盟2024高三5月最后一卷数学试题_2024.5.17高考最后一卷数学

数学参考答案及评分标准 一、二、选择题： 题号 1 2 3 4 5 6 7 8 9 10 11 答案 A B C B D A C D BD ABC BCD 【解析】 1. 依题意A1,0,1,B   y|y 2x,xA     1 ，1，2  ，因此AB1，选项A正确 2  x2 y2 2. 因为双曲线  1的焦距为4，所以3m2 22，解得m2 1，所以则该双曲线经 3 m2 1 3 过一、三象限的渐近线的斜率为  ，选项B正确. 3 3 3. 显然0a 20.4 20 1,b0.40.4 0.40 1,clog 2log 10，故选项C正确. 0.4 0.4 4. 依题意，直线l,m,n不过同一点，因此，若“l,m,n两两相交”则必有“l,m,n共面（由三 个交点确定的平面）”，但若“l,m,n共面”，有可能有两条直线平行，与第三条之间分 别相交，但此时，“l,m,n两两相交”结论错误，故选项B正确. 5. 因为z2 z 10，所以z31(z 1)(z2 z 1)0，从而z3 1，选项D正确. 1 1 1 63r 6. ( x  )6的展开式通项为T Cr ( x)6r ( )r Cr ( )r x 2 当r 2 时，常 2x r1 6 2x 6 2 1 15 1 1 数项为C2( )2  ，选项A正确；令x 1，得各项的系数和为(1 )6  ，选项B 6 2 4 2 64 错误；展开式共7项，二项式系数最大应为第4项，故选项C错误；依题意奇数项二项 1 6 式系数和为C0 C2 C4 C6  Ci 32，选项D错误. 6 6 6 6 2 6 i0  7. 不妨设点A的坐标为(x,y)，OA(x,y),OB (x,y)，   由OA 2 aAB 0可得x2 y2 2x 0，即(x 1)2 y2 1，故选项C正确. 1 1  1 1 8. 依题意S  a  2S S S  S S  S 2 S 2 1， n 2 n a  n n n1 S S n n1 S S n n1 n n n1 n n1 令n 1，解得S 1，从而S 2 n,S  n,a  n  n1，易知选项D正确. 1 n n n 9. 因为0.1+0.4+x+0.2+0.2=1，所以x=0.1，A选项错误； 01234 由E(X)00.110.420.130.240.22，而X  2， 5 故D(X)(02)20.1(12)20.4(22)20.1(32)20.2(42)20.21.8， 因此选项B正确； 又Y=2X-1，所以, E(Y)2E(X)13,D(Y)4D(X)7.2，故C错D对. 2π 10. 由题意，A2,4T 4π，所以T  π，即2，  π π 又f(0)1，所以2sin1，可得 ，因此f(x)2sin(2x  ). 6 6 显然，函数周期为π，f(x π)f(x)，选项A正确； 11π 11π π 因为f( )2sin(  )0，所以选项B正确， 12 6 6 数学参考答案 第1页（共6页） {#{QQABIYAUoggAAJAAABgCAw3QCgGQkBACAIoOhAAMoAIAyQFABAA=}#}7π 14π π 5π f( )2sin(  )2sin 2，选项C正确； 6 6 6 2 π 3π π 3π 2π 5π 若x( , )，即 x  ，则 x  ，函数先减再增，D错误. 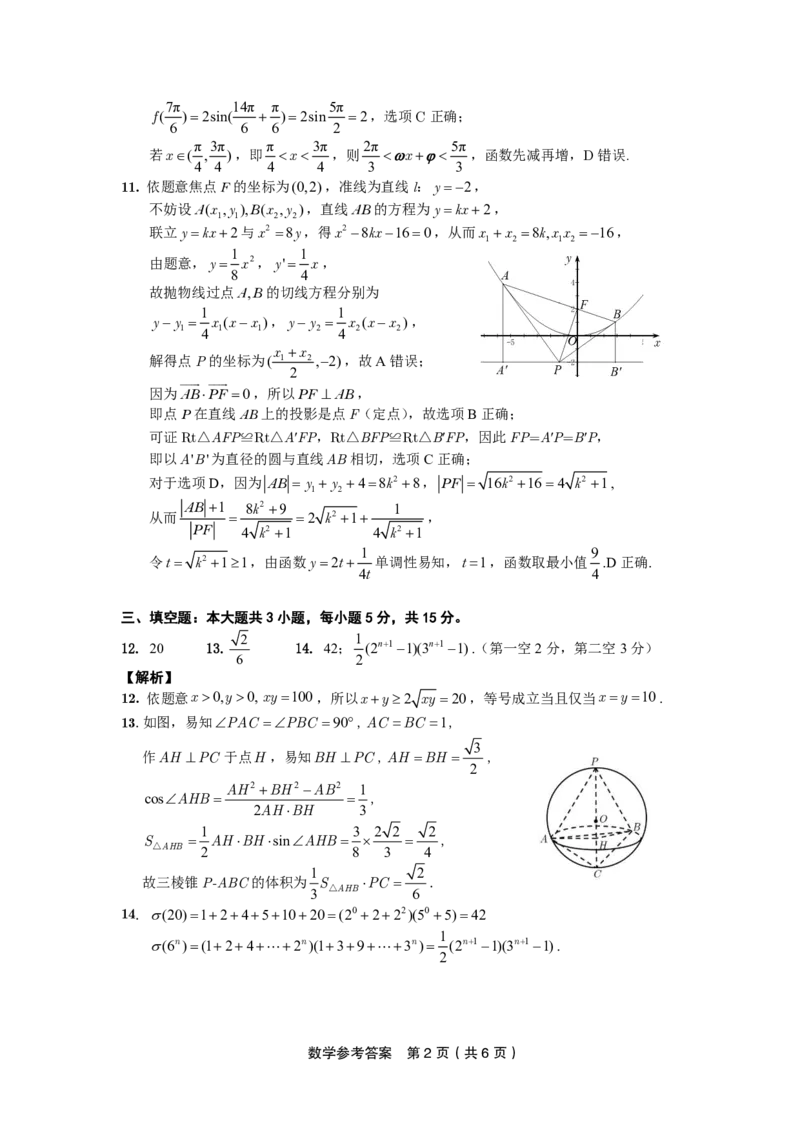4 4 4 4 3 3 11. 依题意焦点F的坐标为(0,2)，准线为直线l：y 2， 不妨设A(x ,y ),B(x ,y )，直线AB 的方程为y kx2， 1 1 2 2 联立y kx2与x2 8y，得x2 8kx160，从而x x 8k,xx 16， 1 2 1 2 1 1 由题意，y  x2，y' x， 8 4 故抛物线过点A,B 的切线方程分别为 1 1 y y  x (xx )，y y  x (xx )， 1 4 1 1 2 4 2 2 x x 解得点P的坐标为( 1 2 ,2)，故A错误； 2   因为ABPF 0，所以PF AB， 即点P在直线AB上的投影是点F（定点），故选项B正确； 可证Rt△AFP≌Rt△AʹFP，Rt△BFP≌Rt△BʹFP，因此FP=AʹP=BʹP， 即以A'B'为直径的圆与直线AB相切，选项C正确； 对于选项D，因为 AB  y  y 48k2 8， PF  16k2 16 4 k2 1, 1 2 AB 1 8k2 9 1 从而  2 k2 1 ， PF 4 k2 1 4 k2 1 1 9 令t  k2 11，由函数y 2t  单调性易知，t 1，函数取最小值 .D正确. 4t 4 三、填空题：本大题共3小题，每小题5分，共15分。 2 1 12. 20 13. 14. 42； (2n11)(3n11).（第一空2分，第二空3分） 6 2 【解析】 12. 依题意x 0,y 0, xy 100，所以x y2 xy 20，等号成立当且仅当x y 10. 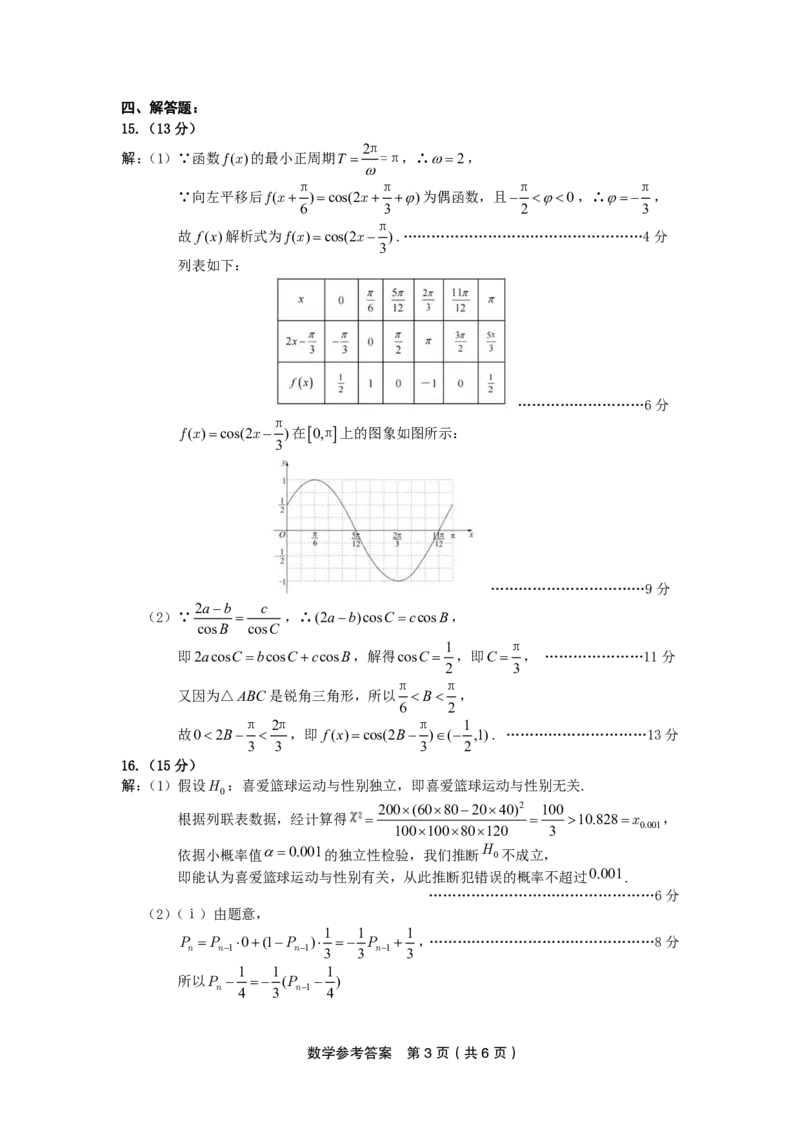13.如图，易知PAC PBC 90,AC BC 1, 3 作AH PC 于点H ，易知BH PC ,AH BH  , 2 AH2 BH2 AB2 1 cosAHB   , 2AH BH 3 1 3 2 2 2 S  AH BH sinAHB    , △AHB 2 8 3 4 1 2 故三棱锥P-ABC的体积为 S PC  . 3 △AHB 6 14. (20)12451020(20 222)(50 5)42 1 (6n)(1242n)(1393n) (2n11)(3n11). 2 数学参考答案 第2页（共6页） {#{QQABIYAUoggAAJAAABgCAw3QCgGQkBACAIoOhAAMoAIAyQFABAA=}#}四、解答题： 15.（13分） 2π 解：（1）∵函数f(x)的最小正周期T  =π，∴2，  π π π π ∵向左平移后f(x  )cos(2x  )为偶函数，且 0，∴ ， 6 3 2 3 π 故 f(x)解析式为f(x)cos(2x  ).……………………………………………4分 3 列表如下： ………………………6分 π f(x)cos(2x  )在0,π上的图象如图所示： 3 ……………………………9分 2ab c （2）∵  ，∴(2ab)cosC ccosB， cosB cosC 1 π 即2acosC bcosCccosB，解得cosC  ，即C  ， …………………11分 2 3 π π 又因为△ABC是锐角三角形，所以 B ， 6 2 π 2π π 1 故02B  ，即 f(x)cos(2B )( ,1). …………………………13分 3 3 3 2 16.（15分） 解：（1）假设H ：喜爱篮球运动与性别独立，即喜爱篮球运动与性别无关. 0 200(60802040)2 100 根据列联表数据，经计算得   10.828x ， 10010080120 3 0.001 依据小概率值0.001的独立性检验，我们推断 H 0不成立， 即能认为喜爱篮球运动与性别有关，从此推断犯错误的概率不超过0.001 . …………………………………………6分 （2）（ⅰ）由题意， 1 1 1 P P 0(1P )  P  ，…………………………………………8分 n n1 n1 3 3 n1 3 1 1 1 所以P   (P  ) n 4 3 n1 4 数学参考答案 第3页（共6页） {#{QQABIYAUoggAAJAAABgCAw3QCgGQkBACAIoOhAAMoAIAyQFABAA=}#}1 3 1 3 1 又P   0，所以{P  }是以 为首项， 为公比的等比数列. …12分 1 4 4 n 4 4 3 3 1 1 （ⅱ）由（ⅰ），P  ( )n1 ， n 4 3 4 3 1 1 1 3 1 1 1 所以P  ( )23  ，P  ( )24   . 24 4 3 4 4 25 4 3 4 4 故甲第25次触球者的概率大. ………………………………………………15分 17.（15分） 解：（1）证明：连接AC . 1 1 因为AB,AB分别为上、下底面的直径，且AB∥AB . 1 1 1 1 所以AA,BB,CC 为圆台母线且交于一点.因此A,A,C,C 四点共面.………3分 1 1 1 1 1 因为圆台OO 中平面ABC ∥平面ABC , 1 1 1 1 平面AACC 平面ABC AC ,平面AACC 平面ABC  AC , 1 1 1 1 1 1 1 1 1 所以AC ∥AC ， 1 1 PA AB 1 又因为AB∥AB,AB  2AB ，所以 1  1 1  ， 1 1 1 1 PA AB 2 PC PA 1 从而 1  1  ，即C 为PC 的中点. …………………………………5分 PC PA 2 1 在△PAC 中，M 为AC 的中点，所以C M∥AA. 1 1 因为AA 平面ABBA ，C M 平面ABBA ， 1 1 1 1 1 1 所以C M∥平面ABBA . ………………………………………………………7分 1 1 1 （2）以O 为坐标原点，OB,OO 分别为y,z轴，过点O 且垂直与平面ABBA 的直线为 1 1 1 x 轴，建立空间直角坐标系O xyz . 因为ABC  30,所以AOC  60,所以A(0,2,0),C( 3,1,0),O (0,0,3)， 1    1 3 1 3 1 因为OC ( 3,1,0)，所以OC  OC ( , ,0)，故C ( , ,3)， 1 1 2 2 2 1 2 2  3 1 所以CC ( , ,3)， ………………………………………………………9分 1 2 2   n OC  0, 设平面OCC 的法向量为n (x ,y ,z )，则 1  1 1 1 1 1 n CC  0,  1  3x y  0,  1 1 即 ，所以平面OCC 的一个法向量为n (1, 3,0). 3 1 1 1  x  y 3z  0,  2 1 2 1 1 …………………………………………11分  又AC ( 3,1,0)，设平面ACC 的法向量为n (x ,y ,z )， 1 2 2 2 2    n AC  0,  3x 2 y 2  0, 所以 2  即 3 1 n CC  0,  x  y 3z  0,  2  2 2 2 2 2 3 所以平面OCC 的一个法向量为n (1, 3, ).……………………………13分 1 2 3 数学参考答案 第4页（共6页） {#{QQABIYAUoggAAJAAABgCAw3QCgGQkBACAIoOhAAMoAIAyQFABAA=}#}设二面角M CC O的大小为, 1 n n 13 39 则cos  n,n  1 2    ， 1 2 n n 1 13 1 2 2 4 3 130 从而sin 1cos2  n,n   ， 1 2 13 130 所以二面角M CC O的正弦值为 . …………………………………15分 1 13 18.（17分） 解：（1）①由题意，且f(x)的定义域为(0,) b a2xa b f '(x)a2xa1  ，……………………………………………………2分 x x f(1)1, a 1, a 1, 依题意 即 从而 ……………………………………4分 f '(1)0, a2 b0, b1, x 1 故f(x) x lnx ，f '(x) ， ………………………………………………5分 x 从而函数f(x)在0,1上单调递减，在1,上单调递增， 所以f(x) f(1)1. …………………………………………………………7分 min b b （2）依题意，xa  lnx 3x 2，其中a 0，记h(x)xa  lnx 3x 2，则h(x)0， a a 因为h(1)0，h(x)h(1)，即h(1)是h(x)的极小值也是最小值，故h'(1)0， b b 而h'(x)axa1 3，所以a 30，解得ba2 3a， ………………9分 ax a 此时h(x)xa (a3)lnx 3x 2(x 0)， 若0a3，则x 0时，xa 0，lnx ,(a3)lnx ,3x 22， 即h(x)，与h(x)0矛盾！ ………………………………………………11分 a3 axa 3x a3 a(xa 1)3(x 1) 若a3，h'(x)axa1 3  ， x x x a(x 1)3(x 1) (a3)(x 1) 则当0x 1时，h'(x)  0，h(x)单调递减， x x a(x 1)3(x 1) (a3)(x 1) 当x 1时，h'(x)  0，h(x)单调递增， x x 符合题意. 故a3. …………………………………………………………………………13分 所以g(a)bkaa2 (3k)a，其中a3. 3k 若 3即k 3时，则函数g(a)在[3,)上最小值为g(3)， 2 1 依题意93(3k)1，解得k  ，符合题意； ………………………………15分 3 3k 3k 若 ＞3即k 3时，则函数g(a)在[3,)上最小值为g( )， 2 2 3k (3k)2 依题意g( )1，即- 1，无解，不符合题意. 2 4 数学参考答案 第5页（共6页） {#{QQABIYAUoggAAJAAABgCAw3QCgGQkBACAIoOhAAMoAIAyQFABAA=}#}1 所以，k  . ………………………………………………………………………17分 3 19.（17分） 1 5 解：（1）依题意，2a CM CM  ,2c M M  AB 1， ………………2分 1 2 2 1 2 c 2 51 所以e   . ……………………………………………………4分 a 1 5 2 （2）设A(x ,y ),A(x ,y ),由题意，矩形ABCD和矩形ABC D 的面积相等， 0 0 1 1 1 1 1 1 1 所以4x y 4x y ， ………………………………………………………………6分 0 0 1 1 x2 y2 x2 即x 2y 2 x 2y 2，而  1y2 b2(1 )， ……… （*） 0 0 1 1 a2 b2 a2 x 2 x 2 从而上式化为b2x 2(1 0 )b2x 2(1 1 )， 0 a2 1 a2 整理可得x 2 x 2 a2，……………………………………………………………9分 0 1 代入（*）式，y 2 y 2 b2， 0 1 故OA 2 OA 2 x 2 y 2 x 2 y 2 a2 b2， 1 0 0 1 1 即OA 2 OA 2为定值，且该定值为a2 b2.……………………………………11分 1 （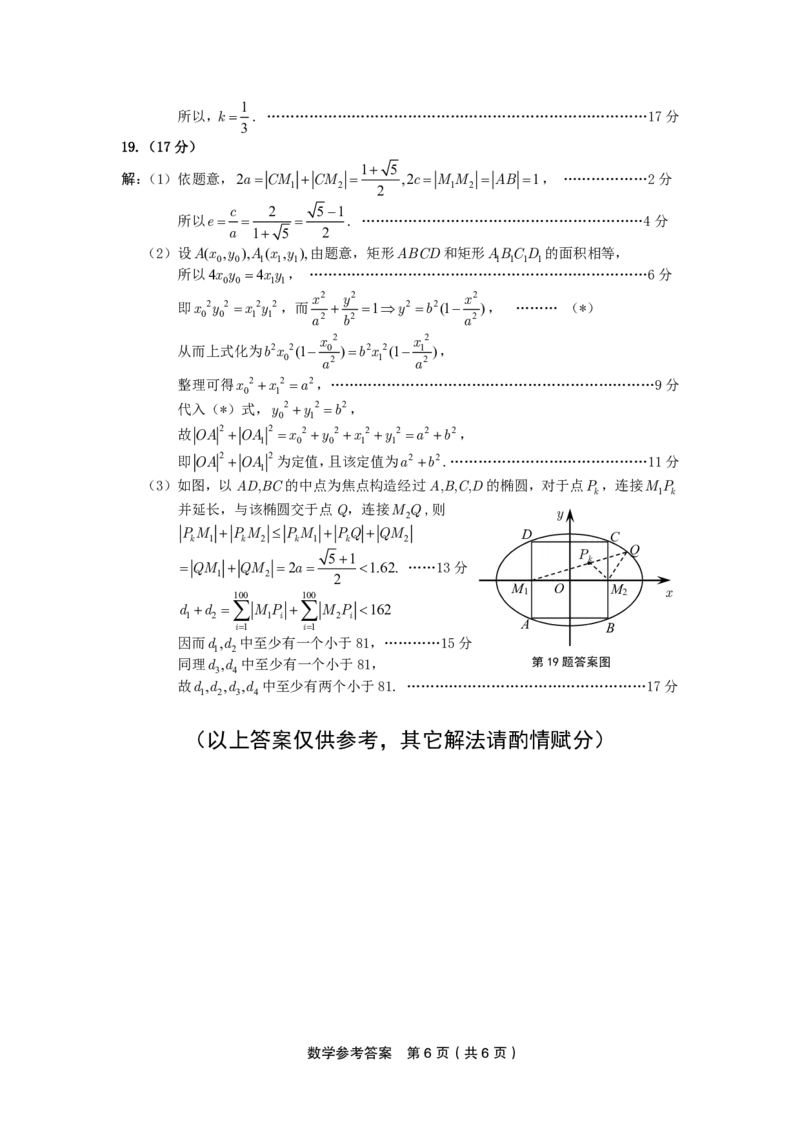3）如图，以AD,BC的中点为焦点构造经过A,B,C,D的椭圆，对于点P ，连接M P k 1 k 并延长，与该椭圆交于点Q，连接M Q,则 y 2 P k M 1  P k M 2  P k M 1  P k Q QM 2 D C ﹒ P Q 51 k QM QM 2a  1.62. ……13分 1 2 2 100 100 M 1 O M 2 x d d M P M P 162 1 2 1 i 2 i i1 i1 A B 因而d ,d 中至少有一个小于81，…………15分 1 2 同理d ,d 中至少有一个小于81， 第19题答案图 3 4 故d ,d ,d ,d 中至少有两个小于81. ……………………………………………17分 1 2 3 4 （以上答案仅供参考，其它解法请酌情赋分） 数学参考答案 第6页（共6页） {#{QQABIYAUoggAAJAAABgCAw3QCgGQkBACAIoOhAAMoAIAyQFABAA=}#}