数学（文）试题_2024年2月_01每日更新_29号_2024届四川省射洪中学高三下学期开学考试_四川省射洪中学2023-2024学年高三下学期开学考试数学（文）PDF版含答案（可编辑）

射洪中学高2021级高三下期入学考试 数学(文科)试题 命题人：龚 旻 审题人：杨 勇 时间：120分钟 满分：150分 第I卷(选择题共60分) 注意事项： 1.答卷前，考生务必将自己的姓名、准考证号等填写在答题卡上。 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干 净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。 3.考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求 的，请将答案涂在答题卡上。 1.已知集合M= x x-1    <2  ，N=-1，0，1，2，3  ，则M∩N= A. 0，1，2  B. 1，2  C. -1，0，1，2  D. 2，3  3-2i 2.若复数z满足z= ，其中i为虚数单位，则z 2+3i  = A.0 B.-1 C. 13 D.1 3.下图是遂宁市2022年4月至2023年3月每月最低气温与最高气温(℃)的折线统计图：已知每月最低气 温与最高气温的线性相关系数r=0.88，则下列结论正确的是 A.月温差(月最高气温-月最低气温)的最大值出现在8月 B.每月最低气温与最高气温有较强的线性相关性，且二者为线性负相关 C.每月最高气温与最低气温的平均值在4-8月逐月增加 D.9-12月的月温差相对于5-8月，波动性更小 4.设等差数列a n  的前n项和为S ，若a =2，则S = n 5 9 A.-18或18 B.-18 C.18 D.2 2 5.△ABC的内角A、B、C的对边分别为a、b、c．已知a= 5，c=2，cosA= ，则b= 3 A. 2 B. 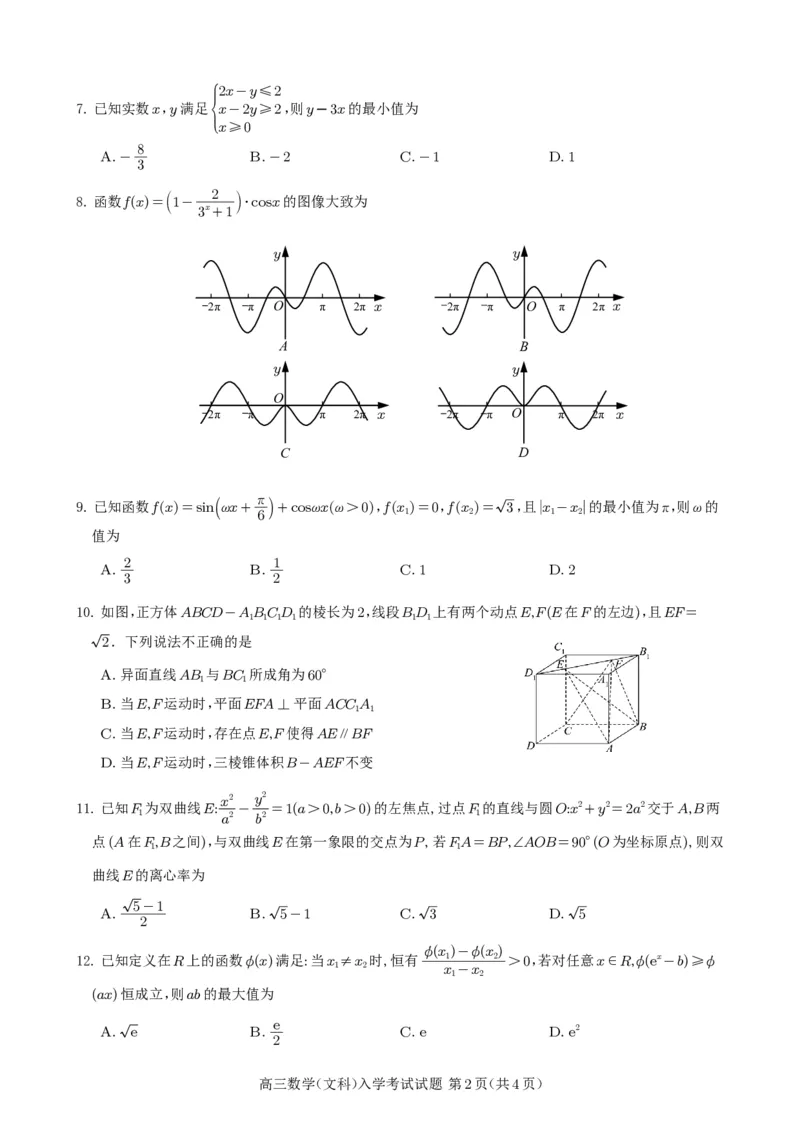3 C.2 D.3 6.下列说法不正确的是 A.若am20，则¬p：∃x ∈R，2x0<0 0 C.回归直线方程为y=1.23x+0.08，则样本点的中心可以为4,5  D.在△ABC中，角A,B,C的对边分别为a,b,c则“A>B”是“sinA>sinB”的充要条件 高三数学（文科）入学考试试题 第1页（共4页）2x-y≤2  7.已知实数x，y满足x-2y≥2，则y-3x的最小值为 x≥0 8 A.- B.-2 C.-1 D.1 3 2 8.函数f(x)=1- 3x+1  ⋅cosx的图像大致为 9.已知函数fx  π =sinωx+ 6  +cosωxω>0  ，fx 1  =0，fx 2  = 3，且x 1 -x 2  y y 2π π O π 2π x 2π π O π 2π x A B y y O 2π π π 2π x 2π π O π 2π x C D 的最小值为π，则ω的 值为 2 1 A. B. C.1 D.2 3 2 10.如图，正方体ABCD-ABCD 的棱长为2，线段BD 上有两个动点E,F(E在F的左边)，且EF= 1 1 1 1 1 1 2．下列说法不正确的是 A.异面直线AB 与BC 所成角为60° 1 1 B.当E,F运动时，平面EFA⊥平面ACCA 1 1 C.当E,F运动时，存在点E,F使得AE∥BF D.当E,F运动时，三棱锥体积B-AEF不变 x2 y2 11.已知F 为双曲线E: - =1(a>0,b>0)的左焦点,过点F 的直线与圆O:x2+y2=2a2交于A,B两 1 a2 b2 1 点(A在F,B之间)，与双曲线E在第一象限的交点为P,若FA=BP,∠AOB=90°(O为坐标原点),则双 1 1 曲线E的离心率为 5-1 A. B. 5-1 C. 3 D. 5 2 ϕ(x)-ϕ(x ) 12.已知定义在R上的函数ϕ(x)满足:当x ≠x 时,恒有 1 2 >0，若对任意x∈R,ϕ(ex-b)≥ϕ 1 2 x -x 1 2 (ax)恒成立，则ab的最大值为 e A. e B. C.e D.e2 2 高三数学（文科）入学考试试题 第2页（共4页）第II卷(非选择题，共90分) 二、填空题：本大题共4个小题，每小题5分，共20分.      13.已知向量a=(-4,x),b=(1,-2)，且(a-2b)⊥b，则x= . 14.已知函数f(x)是定义在R上的奇函数，当x∈(-∞,0)时，f(x)=2x3+x2，则f(2)= ． 2 15.如图，在△ABC中，AB=AC=2，∠BAC= π，D是BC的中点，以AD为折痕把△ACD折叠，使点 3 C到达点C的位置，则当平面CAD⏊平面ABD时，其外接球的体积为 . C B C D A 16.已知点F2,0  为抛物线C：y2=2pxp>0  的焦点，点M-2,0  ,若第一象限内的点P在抛物线C上， PM 则  PF  的最大值为 ． 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题，每个试题考生都必 须作答.第22、23题为选考题，考生根据要求作答. (一)必考题：共60分. 17.本小题12分  习近平总书记在党史学习教育动员大会上强调：“回望过往的奋斗路，眺望前方的奋进 路，必须把党的历史学习好、总结好，把党的成功经验传承好、发扬好．”为庆祝建党100周年，某市积极开 展“青春心向党，建功新时代”系列主题活动．该市某中学为了解学生对党史的认知情况，举行了一次党 史知识竞赛，全校高一和高二共选拔100名学生参加，其中高一年级50人，高二年级50人．并规定将分 数不低于135分的得分者称为“党史学习之星”，这100名学生的成绩(满分为150分)情况如下表所示． 获得“党史学习之星” 未获得“党史学习之星” 总计 高一年级 40 10 50 高二年级 20 30 50 总计 60 40 100 (1)能否有99%的把握认为学生获得“党史学习之星”与年级有关？ (2)获得“党史学习之星”的这60名学生中，按高一和高二年级采用分层抽样﹐随机抽取了6人，再从这 6人中随机抽取2人代表学校参加区里的党史知识竞赛，求这2人中至少有一人是高二年级的概率． nad-bc 参考公式：K2=  2 a+b  c+d  a+c  b+d  ，其中n=a+b+c+d． PK2≥k 0  0.10 0.05 0.025 0.010 0.001 k 2.706 3.841 5.024 6.635 10.828 0 高三数学（文科）入学考试试题 第3页（共4页）18.本小题12分  已知等差数列a n  满足：a +a +a =15,a +a =4a . 1 2 3 8 9 4 (1)求数列a n  的通项公式; 1 (2)记c = ，求数列c n a a n n n+1  的前n项和T. n 19.本小题12分  如图所示，在直四棱柱ABCD-ABCD 中，AB∥CD，AB⊥AD，且AB=AD=1， 1 1 1 1 CD=2，AA =2 2，M是DD 的中点． 1 1 (1)证明BC⊥BM； 1 (2)求点B到平面MBC的距离． 1 20.本小题12分  x2 y2 已知椭圆C: + =1a>b>0 a2 b2  的左右焦点分别是F 1 ,F 2 ，F 1 F 2  =4，点P为椭圆短 轴的端点，且△PFF 的面积为4，过左焦点F 的直线l与椭圆C交于A,B两点(A,B不在x轴上). 1 2 1 (1)求椭圆C的标准方程；   2 2AB (2)若点Q在椭圆C上，且OQ⋅AB=0(O为坐标原点)，求  OQ  的取值范围. 2 21.本小题12分  已知函数fx  =ax-log a x,a∈0,1  ∪1,+∞  ． (1)若a=e，求y=fx  过点0,1  的切线方程； (2)若fx  在其定义域上没有零点，求a的取值范围． (二)选考题：共10分.请考生在第22、23题中选一题作答．如果多做，则按所做的第一题计分． [选修4-4：坐标系与参数方程] 22.本小题10分  在直角坐标系xOy中，已知曲线C 1 :   x y= = 2 2 s + in 2 θ cosθ (θ为参数, θ∈0,π  ),在极坐标系 π 中，曲线C 是以1, 2 2  为圆心且过极点O的圆． (1)分别写出曲线C 普通方程和曲线C 的极坐标方程； 1 2 π (2)直线l:θ= ρ∈R 4  与曲线C 1 、C 2 分别交于M、N两点(异于极点O)，求MN  ． [选修4-5：不等式选讲] 23.本小题10分  已知函数fx  =x-t  +x+t  ，t∈R. (1)若t=1，求不等式fx  ≤8-x2的解集； (2)已知m+n=4，若对任意x∈R，都存在m>0，n>0使得fx  D 1 C 1 B A 1 1 M D C A B 4m2+n = ，求实数t的取值范围. mn 高三数学（文科）入学考试试题 第4页（共4页）