文档内容
银川一中、昆明一中高三联合考试二模文数参考答案
一、选择题
1.已知集合 , ,则 ( )
A. B. C. D.R
解析 .所以
故选C
2.已知单位向量 的夹角为 ,则 ( )
A.0 B.−1 C.1 D.2
解析:
故选A
3.在“五一”国际劳动节来临之际,为持续深化“中国梦·劳动美”主题宣传教育,某校
团委从入团积极分子甲、乙、丙、丁、戊 人中随机选 人去参加“志愿服务进社区”活
动,则甲乙两人中只有 人入选的概率为
A. B. C. D.
【详解】
甲、乙、丙、丁、戊 人中随机选 人共10种方法,甲乙两人中只有 人入选共 种方法,
所以
故选D
4.已知复数 满足 ,则复数 在复平面里位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【详解】令 ,点 在以 为圆心,1为半径的圆上,位于第一象限,
故选A
5.四羊方尊(又称四羊尊)是中国古代青铜器中的杰出代表,展现了商代的高超铸造技术,
其盛酒部分可近似视为一个正四棱台( 上、下底面的边长分别为 ,高为
答案第1页,共2页
学科网(北京)股份有限公司),则四羊方尊的容积约为( )
A. B. C. D.
【详解】由题意可得:四羊方尊的容积约为 .
故选B.
6.有一组样本数据 ,其样本平均数为 ,现加入一个数据 ,组
成新的一组样本数据 ,与原数据相比,关于新的样本数据下列说法一定
错误的是( )
A.平均数不变 B.中位数不变 C.众数不变 D.极差不变
【详解】对A,因为加入一个数据 ,故平均数一定变大,故A错误;
对B,如样本数据1,2,2,3,中位数为2,平均数为2,加入一个新数据3后,中位数仍
为2,故中位数可能不变,故B正确;
对C,众数为数据中出现最多次的数据,故加入一个数据 后,众数可能不变,
故C正确;
对D,加入 后整组数据最大最小值的差不一定改变,即极差可能不变,故D
正确.
故选:A
7.已知两个平面 , ,及两条直线 , ,则下列命题不正确的是( )
A.若 , , , ,则
答案第2页,共2页
学科网(北京)股份有限公司B.若 , , ,则
C.若 , , , ,则
D.若 , 是异面直线, , , , ,则
【详解】对于A,若 ,根据面面垂直的性质定理可得 ,A
正确;
对于B,若 , ,则 ,又 ,则 ,B正确;
对于C,若 ,则 与 可以相交或平行,C错误;
对于D,因为 ,所以存在直线 ,因为 是异面直线,
所以 与 '相交,因为 ,所以 ,又因为 ,
所以 ,D正确.
故选:C
8.若 , , , 则( )
A. B. C. D.
故选:A.
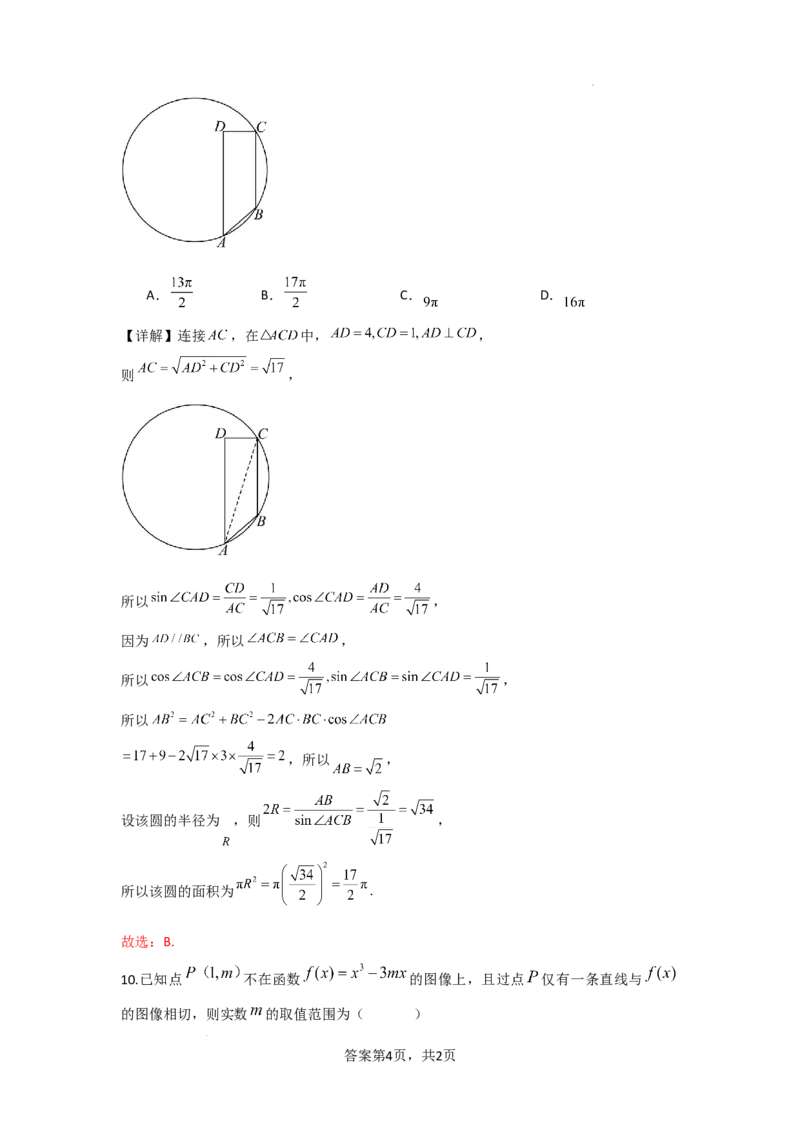
9.在数学探究活动中,某兴趣小组计划制作一个工艺品,设计了如图所示的工艺品图纸,
已 知 四 边 形 的 三 个 顶 点 在 圆 上 , 且 ,
,则该圆的面积为( )
答案第3页,共2页
学科网(北京)股份有限公司A. B. C. D.
【详解】连接 ,在 中, ,
则 ,
所以 ,
因为 ,所以 ,
所以 ,
所以
,所以 ,
设该圆的半径为 ,则 ,
所以该圆的面积为 .
故选:B.
10.已知点 不在函数 的图像上,且过点 仅有一条直线与
的图像相切,则实数 的取值范围为( )
答案第4页,共2页
学科网(北京)股份有限公司A. B.
C. D.
【详解】点 不在函数 的图像上,
则 ,即 ,
设过点 的直线与 的图像相切于 ,
则切线的斜率 ,整理可得 ,
则问题可转化为 只有一个零点,且 ,
令 ,可得 或 ,
当 时, ,则 单调递增,
当 时, ,则 单调递减,
当 时, ,则 单调递增,
即当 时, 有极大值,当 时, 有极小值,
要使 仅有一个零点,
故选:B
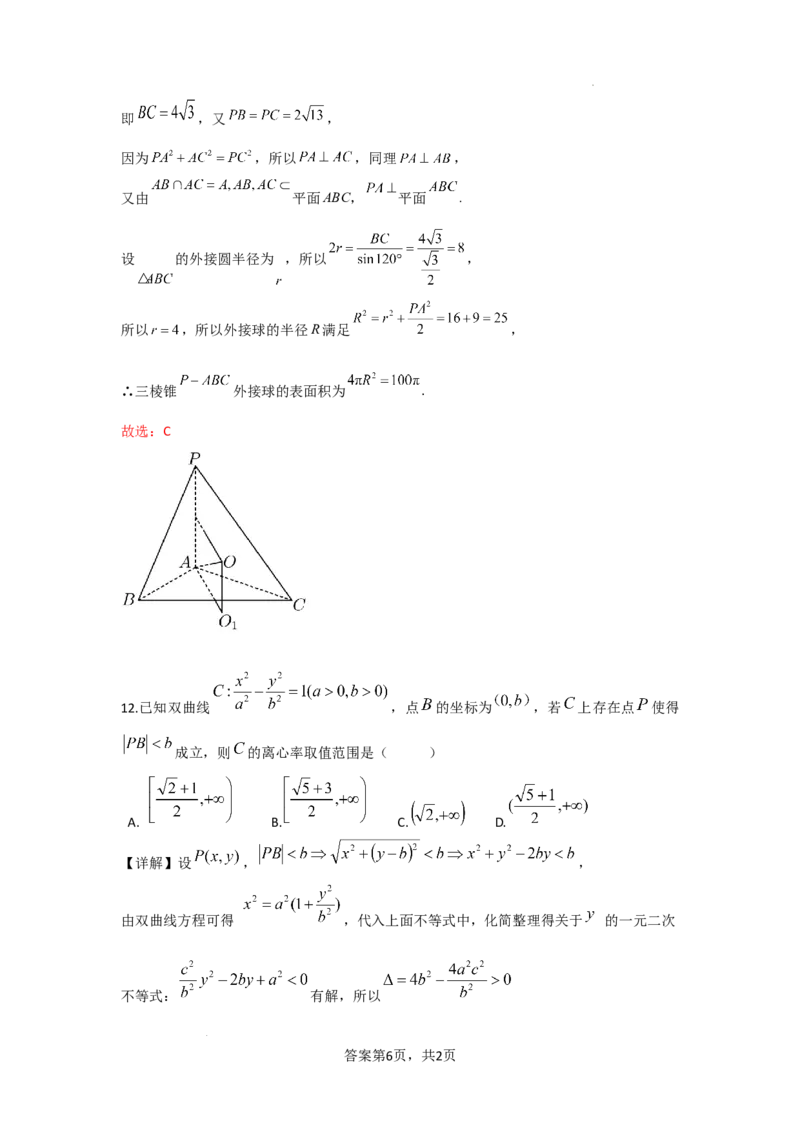
11.在三棱锥 中, , , , ,则三
棱锥 的外接球的表面积为( )
A. B. C. D.
【详解】在 中, ,
答案第5页,共2页
学科网(北京)股份有限公司即 ,又 ,
因为 ,所以 ,同理 ,
又由 平面ABC, 平面 .
设 的外接圆半径为 ,所以 ,
所以 ,所以外接球的半径R满足 ,
∴三棱锥 外接球的表面积为 .
故选:C
12.已知双曲线 ,点 的坐标为 ,若 上存在点 使得
成立,则 的离心率取值范围是( )
A. B. C. D.
【详解】设 , ,
由双曲线方程可得 ,代入上面不等式中,化简整理得关于 的一元二次
不等式: 有解,所以
答案第6页,共2页
学科网(北京)股份有限公司故选:D
二 、填空题
13.若抛物线 过点 ,则该抛物线的准线方程为 .
解析:将点 代入抛物线方程解得 ,所以 ,准线方程为
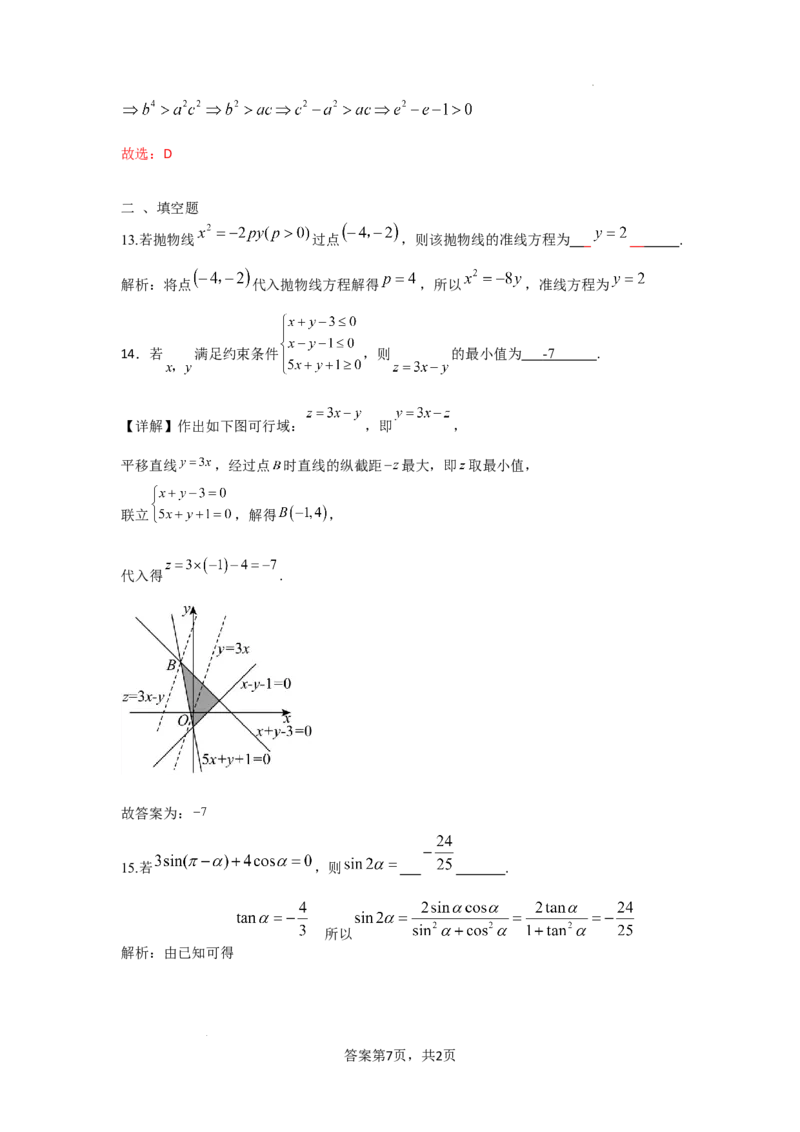
14.若 满足约束条件 ,则 的最小值为 -7 .
【详解】作出如下图可行域: ,即 ,
平移直线 ,经过点 时直线的纵截距 最大,即 取最小值,
联立 ,解得 ,
代入得 .
故答案为:
15.若 ,则 .
所以
解析:由已知可得
答案第7页,共2页
学科网(北京)股份有限公司16.已知函数 的图像关于直线 对称,则
.
【详解】
易得 的定义域为 ,若函数 的图像关于直
线 对称,则其定义域一定关于直线 对称,所以 ,此时必有
, 即 , 解 得 : 。 下 面 验 证 :
所以 ,故 满足题意,得
三、解答题
17.已知数列 的前 项和为 ,且满足
(1)求数列 的通项公式
(2)若 ,求数列 前 项和
解析:(1)当 时,
当 时,
验证:当 , 不成立.所以
(3)由(1)可知
所以,
答案第8页,共2页
学科网(北京)股份有限公司18. 近年来,短视频作为以视频为载体的聚合平台,社交属性愈发突出,在用户生活中覆
盖面越来越广泛,针对短视频的碎片化缺陷,将短视频剪接成长视频势必成为一种新的技
能.某机构在网上随机对1000人进行了一次市场调研,以决策是否开发将短视频剪接成长
视频的APP,得到如下数据:
青年人 中年人 老年人
对短视频剪接成长视频的APP有需求 200
对短视频剪接成长视频的APP无需求 150
其中的数据为统计的人数,已知被调研的青年人数为400.
(1)求 的值;
(2)判断是否有 的把握认为对短视频剪接成长视频的APP需求,青年人与中老年
人是否有差异?
参考公式: ,其中 .
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
【小问1详解】
由题意可得: ,解得 .
【小问2详解】
零假设为 :对短视频剪接成长视频APP的需求,青年人与中老年人没有差异.
由已知得,如下 列联表:
答案第9页,共2页
学科网(北京)股份有限公司青年人 中老年人 合计
对短视频剪接成长视频的APP有需求 300 250 550
对短视频剪接成长视频的APP无需求 100 350 450
合计 400 600 1000
可得 ,
所以有 的把握认为对短视频剪接成长视频的APP的需求,青年人与中老年人有差异.
19.已知函数 ,其中 .
(1)当 时,求曲线 在 处的切线方程;
(2)讨论 的极值。
【详解】(1)
,
当 时, , ,
又 ,故曲线 在 处的切线方程为 ;
(2) ,解得知 , ,
①若 ,可得 或 时, ,当 时, ,
所以 在 , 递减, 递增,
答案第10页,共2页
学科网(北京)股份有限公司②若 ,则 ,所以函数单调递减,无极值;
③若 ,当 或 时, ,当 时, ,
所以 在 , 递减, 递增,
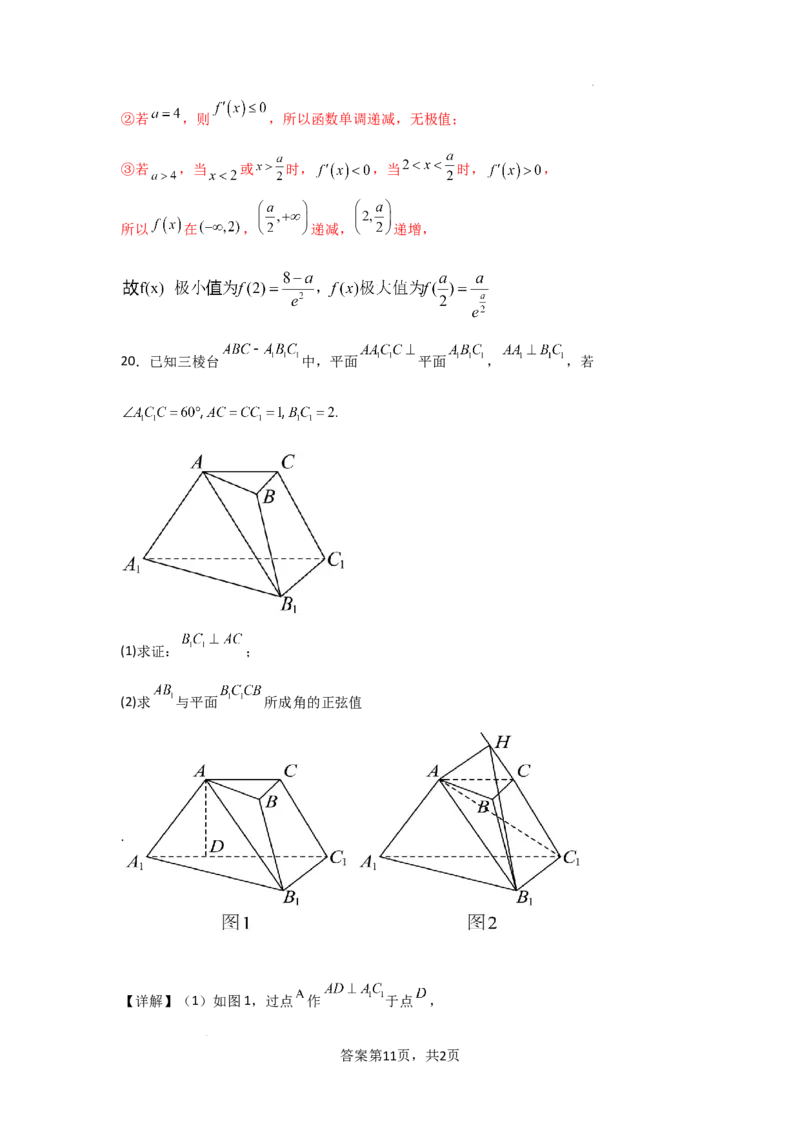
20.已知三棱台 中,平面 平面 , ,若
(1)求证: ;
(2)求 与平面 所成角的正弦值
.
【详解】(1)如图1,过点 作 于点 ,
答案第11页,共2页
学科网(北京)股份有限公司因为平面 平面 ,平面 平面 , 平面 ,
所以 平面 ,又因为 平面 ,所以 ,
因为 , ,且 平面 ,
所以 平面 ,因为 平面 ,
所以 .
(2)如图2延长 ,过点 作 于点 ,连接 ,
由(1)可知 平面 ,因为 平面 ,
所以 ,又 ,且 , 平面 ,
所以 平面 ,则 为 与平面 所成角,
在 中, ,所以 ,
因为四边形 为梯形,所以 ,所以 ,
在 中, ,
又 平面 , 平面 ,所以 ,
则 ,
所以 .
即 与平面 所成角的正弦值为 .
21.已知直线 与椭圆 交于A,B两点,若椭圆 上存在C,D
两点关于直线l对称.
答案第12页,共2页
学科网(北京)股份有限公司(1)求实数m的取值范围;
(2)若O为坐标原点,当 的面积最大时,求直线l的方程.
【详解】(1)由题意C,D关于直线l对称,所以设直线 的方程为 ,
, ,
由 ,消去y得 ,
所以 ,得 ,①
则 , .
设 的中点为 ,则 , ,故 .
将 代入 ,得 ,所以 ,
将 代入①得 ,解得 .
故实数m的取值范围为
(2)由(1)得
,
坐标原点O到直线 的距离 ,
所以
答案第13页,共2页
学科网(北京)股份有限公司,
当且仅当 ,即 时取等号,
当 时, ,当 时, .
故当 的面积最大时,直线l的方程为 或 .
选做题
22.(本小题满分10分)【选修4-4:坐标系与参数方程】
在平面直角坐标系 中,曲线 的参数方程为 ( 为参数).以坐标原点
为极点, 轴正半轴为极轴建立极坐标系,直线 的极坐标方程为 .
(1)求 的普通方程和 的直角坐标方程;
(2)设直线 与 轴相交于点 ,动点 在 上,点 满足 ,点 的轨迹为 ,
试判断曲线 与曲线 是否有公共点.若有公共点,求出其直角坐标;若没有公共点,请说
明理由.
【详解】(1)由题设曲线 的参数方程,消参得 ,
由 ,且 得,
,化简得 ,
C的普通方程为 ,l直角坐标方程为 .
(2)当 时, ,易知 ,设 ,
答案第14页,共2页
学科网(北京)股份有限公司可得 ,
(a是参数),
消参得方程为 且 ,
则圆心距离 得 ,
则两圆相交,故两圆存在公共点,联立方程组 ,
解得 或 ,故坐标为 .
23.(选项4-5不等式选讲)(本小题满分10分)
(1)当 时,求不等式 的解集;
(2)若 ,求 的取值范围.
【详解】(1)当 时, ,
因为 ,所以 或 或 ,
解得 或 ,故不等式 的解集为 ;
(2)因为 ,当 时, 成立;
答案第15页,共2页
学科网(北京)股份有限公司当 时, ,此时 ,
明显函数 在 上单调递减,在 上单调递增,
故 ,解得 ,又 ,所以 ;
综上所述, 的取值范围是 .
答案第16页,共2页
学科网(北京)股份有限公司