文档内容
2024年新高考改革适应性练习(九省联考题型)
数学参考答案
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.)
题号 1 2 3 4 5 6 7 8
答案 D C B C A A D C
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得3分,有选错的得0分.)
题号 9 10 11
答案 ABD BD ABD
三、填空题(本题共3小题,每小题5分,共15分.)
题号 12 13 14
答案 5或6
1
�− ,0� �√5−1,√5+1�
2
四、解答题(本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.)
15.(13分)
(1)设 ,则有 ,则 ,因为 是 的中点,所以 ,
2 𝑥𝑥0
𝐴𝐴(𝑥𝑥0,𝑦𝑦0) 𝑦𝑦0 = 2𝑥𝑥0 𝐵𝐵(0,𝑦𝑦0) 𝑃𝑃 𝐴𝐴𝐵𝐵 𝑃𝑃�2 ,𝑦𝑦0�
则 ,即 ,故点 在抛物线 的上运动.
2 𝑥𝑥0 2 2
𝑦𝑦0 = 2𝑥𝑥0 = 4�2� 𝑦𝑦𝑃𝑃 = 4𝑥𝑥𝑃𝑃 𝑃𝑃 𝛤𝛤1:𝑦𝑦 =4𝑥𝑥(𝑦𝑦 > 0) (4分)
(2)因为 与 平行,所以四边形 是梯形,
其上底为 𝐴𝐴𝑃𝑃 𝐹𝐹1𝐹𝐹2 ,下底为 𝐴𝐴𝑃𝑃𝐹𝐹1𝐹𝐹2 ,高为 ,
1 1 𝑝𝑝1 𝑝𝑝2
𝐴𝐴𝑃𝑃 = 2𝑥𝑥𝐴𝐴 = 2𝑥𝑥0 𝐹𝐹1𝐹𝐹2 = 2 − 2 = 2−1 =1 𝑦𝑦𝐴𝐴 = 𝑦𝑦0
所以其面积 ,又 ,所以
2
𝑦𝑦0 1 2 𝑦𝑦0 𝑦𝑦0 1 3 𝑦𝑦0
𝑆𝑆 = 2 �2𝑥𝑥0+1� 𝑦𝑦0 = 2𝑥𝑥0 𝑆𝑆 = 2 �4 +1�= 8𝑦𝑦0 + 2 (𝑦𝑦0 > 0) (8分)
令 ,则 ,所以 即 关于 单调递增,
1 3 𝑦𝑦0 ′ 3 2 1
𝑓𝑓(𝑦𝑦0)= 8𝑦𝑦0 + 2 (𝑦𝑦0 > 0) 𝑓𝑓 (𝑦𝑦0)= 8𝑦𝑦0 +2 > 0 𝑓𝑓(𝑦𝑦0) 𝑆𝑆 𝑦𝑦0
数学参考答案 第1页(共6页)
学科网(北京)股份有限公司(10分)
又当 时, ; 时, ,所以 在 上没有最值.
𝑦𝑦0 →0 𝑆𝑆 →0 𝑦𝑦0 → +∞ 𝑆𝑆 → +∞ 𝑆𝑆 𝑦𝑦0 ∈ (0,+∞) (13分)
16.(15分)
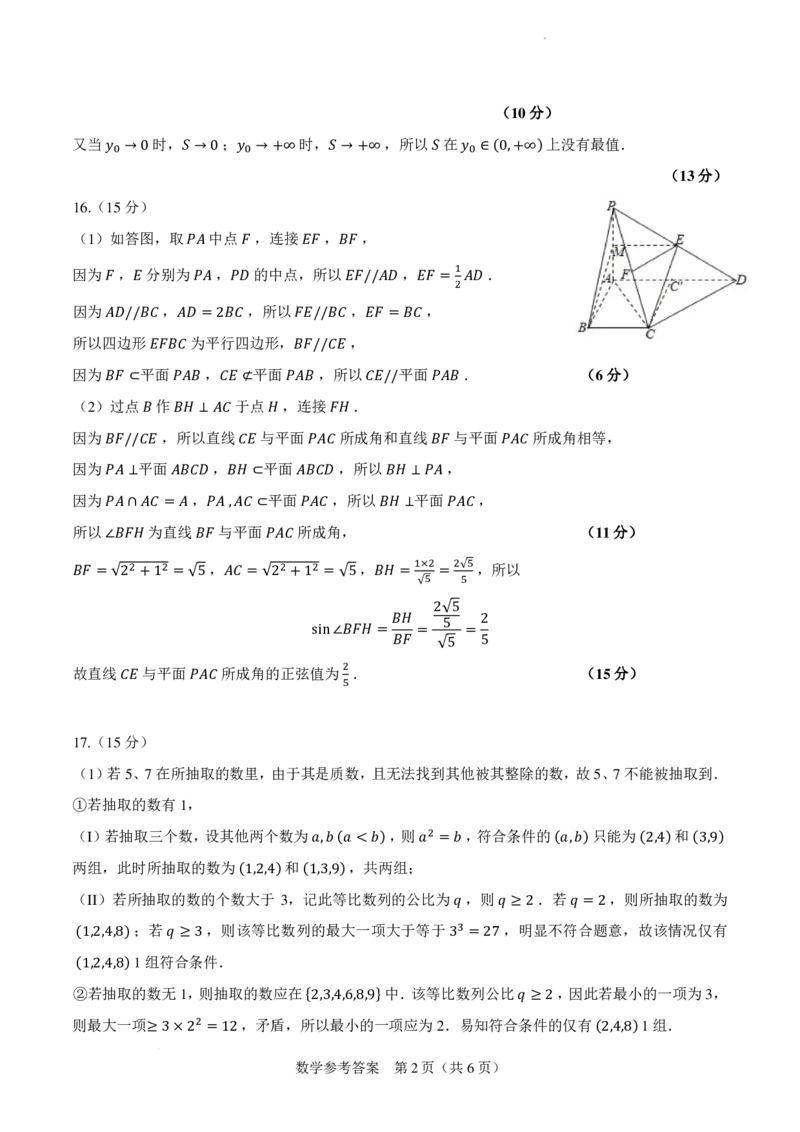
(1)如答图,取 中点 ,连接 , ,
因为 , 分别为 𝑃𝑃𝐴𝐴 , 𝐹𝐹 的中点, 𝐸𝐸𝐹𝐹所 以𝐵𝐵𝐹𝐹 , .
1
因为 𝐹𝐹 𝐸𝐸 , 𝑃𝑃𝐴𝐴 𝑃𝑃𝑃𝑃, 所以 𝐸𝐸,𝐹𝐹//𝐴𝐴𝑃𝑃 𝐸𝐸,𝐹𝐹 = 2𝐴𝐴𝑃𝑃
所以 四𝐴𝐴𝑃𝑃边/形/𝐵𝐵𝐵𝐵 𝐴𝐴𝑃𝑃为=平2行𝐵𝐵𝐵𝐵四 边形, 𝐹𝐹𝐸𝐸//𝐵𝐵𝐵𝐵 , 𝐸𝐸𝐹𝐹 = 𝐵𝐵𝐵𝐵
因为 平 𝐸𝐸面𝐹𝐹𝐵𝐵𝐵𝐵 , 平面 𝐵𝐵𝐹𝐹/,/𝐵𝐵所𝐸𝐸 以 平面 . (6分)
(2) 𝐵𝐵过𝐹𝐹点⊂ 作 𝑃𝑃𝐴𝐴𝐵𝐵 𝐵𝐵𝐸𝐸于⊄点 , 𝑃𝑃𝐴𝐴连𝐵𝐵接 . 𝐵𝐵 𝐸𝐸// 𝑃𝑃𝐴𝐴𝐵𝐵
因为 𝐵𝐵 , 𝐵𝐵所𝐵𝐵以⊥直𝐴𝐴线𝐵𝐵 与 𝐵𝐵平 面 𝐹𝐹𝐵𝐵所 成角和直线 与平面 所成角相等,
因为 𝐵𝐵𝐹𝐹//平𝐵𝐵𝐸𝐸面 , 𝐵𝐵𝐸𝐸 平面 𝑃𝑃𝐴𝐴𝐵𝐵 ,所以 𝐵𝐵𝐹𝐹, 𝑃𝑃𝐴𝐴𝐵𝐵
因为 𝑃𝑃𝐴𝐴 ⊥ 𝐴𝐴𝐵𝐵𝐵𝐵,𝑃𝑃 𝐵𝐵𝐵𝐵 ⊂ 平面 𝐴𝐴𝐵𝐵𝐵𝐵𝑃𝑃, 所以 𝐵𝐵𝐵𝐵 ⊥平𝑃𝑃面𝐴𝐴 ,
所以 𝑃𝑃𝐴𝐴∩𝐴𝐴为𝐵𝐵 直=线𝐴𝐴 𝑃𝑃𝐴𝐴与 ,平𝐴𝐴𝐵𝐵面⊂ 所 𝑃𝑃𝐴𝐴成𝐵𝐵角 , 𝐵𝐵 𝐵𝐵 ⊥ 𝑃𝑃𝐴𝐴𝐵𝐵 (11分)
∠𝐵𝐵𝐹𝐹𝐵𝐵 𝐵𝐵𝐹𝐹, 𝑃𝑃𝐴𝐴𝐵𝐵 , ,所以
2 2 2 2
1×2 2√5
𝐵𝐵𝐹𝐹 = √2 +1 = √5 𝐴𝐴𝐵𝐵 = √2 +1 = √5 𝐵𝐵𝐵𝐵 = √5 = 5
2√5
𝐵𝐵𝐵𝐵 2
5
sin∠𝐵𝐵𝐹𝐹𝐵𝐵 = = =
故直线 与平面 所成角的正弦值为 . 𝐵𝐵𝐹𝐹 √ 5 5 (15分)
2
𝐵𝐵𝐸𝐸 𝑃𝑃𝐴𝐴𝐵𝐵 5
17.(15分)
(1)若5、7在所抽取的数里,由于其是质数,且无法找到其他被其整除的数,故5、7不能被抽取到.
①若抽取的数有1,
(I)若抽取三个数,设其他两个数为 ,则 ,符合条件的 只能为 和
2
两组,此时所抽取的数为 和 𝑎𝑎,𝑏𝑏 (𝑎𝑎,<共𝑏𝑏两) 组; 𝑎𝑎 = 𝑏𝑏 (𝑎𝑎,𝑏𝑏) (2,4) (3,9)
(II)若所抽取的数的个数 (1大,2于,4)3 , (记1,此3,9等) 比数列的公比为 ,则 .若 ,则所抽取的数为
;若 ,则该等比数列的最大一项大于等于 𝑞𝑞 𝑞𝑞,≥明2显 不符 𝑞𝑞合=题2 意,故该情况仅有
3
(1,2,4,8) 1组符 𝑞𝑞合≥条3 件. 3 =27
②(1若,2,抽4,8取) 的数无1,则抽取的数应在 中.该等比数列公比 ,因此若最小的一项为3,
则最大一项 ,矛盾,所 {2以,3最,4,小6,8的,9一} 项应为2.易知符合 𝑞𝑞条≥件2的 仅有 1组.
2
≥ 3×2 = 12 (2,4,8)
数学参考答案 第2页(共6页)
学科网(北京)股份有限公司综合上述情况,仅有 , , , 共4组符合条件. (4分)
而抽取的所有结果共 有(1,2,4) (1,3,9)种 ,(1故,2概,4,率8) (2,4,8.) (6分)
9 4
(2)①当抽取的数有3 2项时−1,(= I)51若1 该等差数列的 𝑃𝑃公=差511 ,则有 , ,…, 共
7 组符合条件.(II)若该等差数列的公差 ,则有 𝑑𝑑 = 1 , (1,2,,3…) ,(2,3,4) 共 5 (组7,符8,9合) 条
件.(III)若该等差数列的公差 ,则 有𝑑𝑑 = 2 , (1,3,5,) (2,4,6共) 3组符(合5,条7,9件) .(IV)若该等
差数列的公差 ,则仅有 𝑑𝑑 = 3 1 组符合 (1条,4件,7). ((V2),5,若8)该 等(3差,6数,9)列 的公差 ,则没有满足条
件的选取组合 .𝑑𝑑 = 4 (1,5,9) 𝑑𝑑 ≥ 5
故此情况共有 组符合条件. (8分)
②当抽取的数 有7+45项+时3,(+1I)=若1该6 等差数列的公差 ,则有 , ,…, 共
6 组符合条件.(II)若该等差数列的公差 , 𝑑𝑑则=有1 (,1,2,3,4) (,2,3,4,5) 共 3(6组,7,符8,9合) 条
件.(III)若该等差数列的公差 ,则 𝑑𝑑没=有2满 足条件 (的1,选3,5取,7组) 合(.2,4 ,6,8) (3,5,7,9)
故此情况共有 组符合 条𝑑𝑑 件≥.3 (10分)
③当抽取的数 有6+53项=时9,( I)若该等差数列的公差 ,则有 , ,…,
共 5 组符合条件.(II)若该等差数列的公差 𝑑𝑑,=则1 仅有 (1,2,3,4,51) 组(符2,3合,4条,5件,6). (III)(5若,6该,7,等8,9差)
数列的公差 ,则没有满足条件的选取组 𝑑𝑑合=.2 (1,3,5,7,9)
故此情况共 有𝑑𝑑 ≥ 3 组符合条件. (12分)
以此类推, 5当+抽1 =取66 、7、8、9 项时,都当且仅当公差为 1 时有符合条件的选取组合,分别有4、
3、2、1组,
综上所述,满足条件的选取组合共有 组, (14分)
由(1),抽取的所有结果共有 16种+,9故+概6+率4+3+2.+ 1 = 41 (15分)
9 41
2 −1 = 511 𝑃𝑃2 = 511
18.(17分)
(1) , , (2分)
观察得𝑓𝑓(𝑥𝑥)= 𝑎𝑎𝑥𝑥−,(即𝑥𝑥+2)ln为(𝑥𝑥其+零1)点 ,𝑥𝑥 ∈(− 1,+ ∞) (4分)
微信公众号:智慧学库
𝑓𝑓(0) = 0 𝑥𝑥 = 0
′ 1
所以 ,即 𝑓𝑓.(故𝑥𝑥)=的𝑎𝑎值−为1−2. − ln( 𝑥𝑥+1 ) (6分)
𝑥𝑥+1
′
(2) 𝑓𝑓由(0()1=)𝑎𝑎得−2 = 0 必 𝑎𝑎经=过2原 点, 𝑎𝑎若 需使 经过四个象限,则 需在区间 和
上均至少 𝑦𝑦存=在𝑓𝑓一(𝑥𝑥个) 零点, 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) 𝑓𝑓(𝑥𝑥) (−1,0)
(0,+∞)
数学参考答案 第3页(共6页)
学科网(北京)股份有限公司令 在 和 上均有根.
(𝑥𝑥+2)ln(𝑥𝑥+1)
𝑓𝑓(𝑥𝑥)= 𝑎𝑎𝑥𝑥−(𝑥𝑥+2)ln(𝑥𝑥+1)= 0 ⟹ 𝑎𝑎 = 𝑥𝑥 (𝑥𝑥 ≠ 0) (−1,0) (0,+∞)
设函数 , ,
2
(𝑥𝑥+2)ln(𝑥𝑥+1) ′ 𝑥𝑥 +2𝑥𝑥−2(𝑥𝑥+1)ln(𝑥𝑥+1)
令 𝑔𝑔(𝑥𝑥)= 𝑔𝑔 (𝑥𝑥,)= 2 ,
𝑥𝑥 (𝑥𝑥+1)𝑥𝑥
2 ′
令 ℎ(𝑥𝑥)= 𝑥𝑥 +2𝑥𝑥−2(𝑥𝑥,+1)ln(𝑥𝑥+1), 当ℎ (𝑥𝑥)= 2[𝑥𝑥−时l,n(𝑥𝑥+1)] , 单调递减;当
′ 𝑥𝑥 ′
时 ,𝜑𝜑(𝑥𝑥)= 𝑥𝑥−l,n(𝑥𝑥+1单) 调𝜑𝜑递(𝑥𝑥增).=所𝑥𝑥+以1 𝑥𝑥 ∈是(−1,0)的 极小𝜑𝜑值(𝑥𝑥点)<,0 𝜑𝜑(𝑥𝑥) . 𝑥𝑥 ∈ (0,+∞)
′
所以𝜑𝜑 (𝑥𝑥)> 0 恒成𝜑𝜑(立𝑥𝑥), 即 , 故𝑥𝑥 = 0 单 𝜑𝜑调(𝑥𝑥递) 增.又 𝜑𝜑(𝑥𝑥,)m所in以=当𝜑𝜑(0) = 0 时,
′
𝜑𝜑(𝑥𝑥),≥即0 , ℎ所(以𝑥𝑥)≥ 0 单调 ℎ递(𝑥𝑥减) ;当 ℎ(时0),= 0 𝑥𝑥 ∈(,−1即,0) ℎ(𝑥𝑥),<
′ ′ ′ ′
ℎ所(以0)= 0 单调 𝑔𝑔递(增𝑥𝑥).< 0 𝑔𝑔(𝑥𝑥) 𝑥𝑥 ∈ (0,+∞) ℎ(𝑥𝑥)> ℎ (0)= 0 𝑔𝑔 (𝑥𝑥)> 0
又当 𝑔𝑔(𝑥𝑥) 时, ,所以要使得 在 和 上均有根, 需满足 .
综上 所𝑥𝑥述→,0 若 𝑔𝑔(𝑥𝑥)的→图2像 经过四个象 限𝑔𝑔(,𝑥𝑥)则= 𝑎𝑎 (−1,0) . (0 ,+∞ ) (𝑎𝑎 17分) 𝑎𝑎 ∈(2,+∞)
(方法不唯一 ,𝑓𝑓(若𝑥𝑥)考 生从极值点等其他角度入 𝑎𝑎手∈,(2依,+据∞实) 际情况酌情赋分)
19.(17分)
(1)我们需证 在普通加法下可构成一个群,由题意,需从以下四个方面进行验证:
①封闭性:对 𝑅𝑅 ,则 ,封闭性成立. (1分)
②结合律:对 𝑎𝑎,𝑏𝑏 ∈ 𝑅𝑅 , 𝑎𝑎+𝑏𝑏 ∈ 𝑅𝑅 ,结合律成立. (2分)
③恒等元:取 𝑎𝑎,𝑏𝑏,𝑐𝑐 ∈𝑅𝑅 ,𝑎𝑎则+对(任𝑏𝑏+意𝑐𝑐) = (𝑎𝑎,+𝑏𝑏)+𝑐𝑐 .符合恒等元要求. (3分)
④逆:对任意 𝑒𝑒 = 0 ∈,𝑅𝑅 , 𝑎𝑎且∈ 𝑅𝑅 0+𝑎𝑎 = 𝑎𝑎 ,满足逆的存在性.
𝑎𝑎 ∈ 𝑅𝑅 𝑏𝑏 = −𝑎𝑎 ∈𝑅𝑅 𝑎𝑎+𝑏𝑏 = 𝑎𝑎+(−𝑎𝑎)= 0 = 𝑒𝑒 (4分)
综上所述,所有实数在普通加法运算下可构成群 .
+
(2)首先提出, 的“×”运算可以是复数的乘 𝑅𝑅法: ,理由如下.
𝐵𝐵 𝑧𝑧1𝑧𝑧2 (∀𝑧𝑧1,𝑧𝑧2 ∈ 𝐵𝐵) (6分)
即证明 在普通乘法下可构成一个群,同(1),需从四方面进行验证:
①封闭 性𝑆𝑆 :设 , ,其中 ,即 .
2 2 2 2
则 𝑧𝑧1 = 𝑎𝑎+𝑏𝑏i 𝑧𝑧2 = 𝑐𝑐+𝑑𝑑i 𝑧𝑧1,𝑧𝑧2,∈ 𝐵𝐵 𝑎𝑎 +𝑏𝑏 = 𝑐𝑐 +𝑑𝑑 = 1
所以 𝑧𝑧1𝑧𝑧2 = (𝑎𝑎+𝑏𝑏i)(𝑐𝑐+𝑑𝑑i)= (𝑎𝑎𝑐𝑐−𝑏𝑏𝑑𝑑)+(𝑎𝑎𝑑𝑑+𝑏𝑏𝑐𝑐)i
2 2 2 2 2 2 2 2 2 2
|𝑧𝑧1𝑧𝑧2|= �(𝑎𝑎𝑐𝑐−𝑏𝑏𝑑𝑑) +(𝑎𝑎𝑑𝑑+𝑏𝑏𝑐𝑐) = √𝑎𝑎 𝑐𝑐 +𝑏𝑏 𝑑𝑑 +𝑎𝑎 𝑑𝑑 +𝑏𝑏 𝑐𝑐
,即 ,封闭性成立. (7分)
2 2 2 2 2 2 2 2
=②结�𝑐𝑐合(律𝑎𝑎 :+设𝑏𝑏 )+𝑑𝑑 (𝑎𝑎 +,𝑏𝑏 )=√𝑐𝑐 +,𝑑𝑑 = 1 𝑧𝑧1,𝑧𝑧2其∈中𝐵𝐵 ,
𝑧𝑧1 = 𝑎𝑎+𝑏𝑏i 𝑧𝑧2 = 𝑐𝑐+𝑑𝑑i 𝑧𝑧3 = 𝑒𝑒+𝑓𝑓i 𝑧𝑧1,𝑧𝑧2,𝑧𝑧3 ∈ 𝐵𝐵
数学参考答案 第4页(共6页)
学科网(北京)股份有限公司𝑧𝑧1(𝑧𝑧2𝑧𝑧3)= (𝑎𝑎+𝑏𝑏i)[(𝑐𝑐𝑒𝑒−𝑑𝑑𝑓𝑓)+(𝑐𝑐𝑓𝑓+𝑑𝑑𝑒𝑒)i]
= [𝑎𝑎(𝑐𝑐𝑒𝑒−𝑑𝑑𝑓𝑓)−𝑏𝑏(𝑐𝑐𝑓𝑓+𝑑𝑑𝑒𝑒)]+[𝑎𝑎(𝑐𝑐𝑓𝑓+𝑑𝑑𝑒𝑒)+𝑏𝑏(𝑐𝑐𝑒𝑒 −𝑑𝑑𝑓𝑓)]i
(𝑧𝑧1𝑧𝑧2)𝑧𝑧3 = [(𝑎𝑎𝑐𝑐−𝑏𝑏𝑑𝑑)+(𝑎𝑎𝑑𝑑+𝑏𝑏𝑐𝑐)i](𝑒𝑒+𝑓𝑓i)
对比后容易发现, = [𝑒𝑒和(𝑎𝑎𝑐𝑐−𝑏𝑏𝑑𝑑)−实𝑓𝑓部(𝑎𝑎和𝑑𝑑+虚𝑏𝑏部𝑐𝑐)分]+别[对𝑓𝑓(应𝑎𝑎𝑐𝑐相−等𝑏𝑏,𝑑𝑑即)+𝑒𝑒(𝑎𝑎𝑑𝑑+𝑏𝑏𝑐𝑐)] ,结合律成立.
𝑧𝑧 1(𝑧𝑧2 𝑧𝑧3) (𝑧𝑧 1𝑧𝑧2)𝑧𝑧 3 ( 𝑧𝑧18(分𝑧𝑧2𝑧𝑧)3) = (𝑧𝑧1𝑧𝑧2)𝑧𝑧3
③恒等元:取 ,则对任意 , ,符合恒等元要求. (9分)
④逆的存在性 :𝑒𝑒对=任1意∈ 𝐵𝐵 𝑧𝑧,∈取𝐵𝐵 其共1·轭𝑧𝑧 =𝑧𝑧 ,则 ,满足逆的存
2 2
在性. 𝑧𝑧 = 𝑎𝑎+ 𝑏𝑏i∈ 𝐵𝐵 𝑧𝑧̅ = 𝑎𝑎− 𝑏𝑏i (1 0𝑧𝑧·分𝑧𝑧̅)= 𝑎𝑎 +𝑏𝑏 = 1 = 𝑒𝑒
综上所述, 在复数的乘法运算下构成一个群 .
×
(构造不唯𝐵𝐵一 ,证明方法也不唯一,本题较为 𝐵𝐵开放 ,不同的方法应据实际情况酌情赋分)
(3)所有阶数小于等于四的群 都是阿贝尔群,理由如下. (11分)
×
若群 的阶数为0,则 为空 集𝐺𝐺, 与定义矛盾.所以 的阶数为1,2,3,4.下逐一证明.
× ×
①若 群𝐺𝐺 的阶数为1, 则𝐺𝐺 其唯一的元素为其恒等元,明 𝐺𝐺显 符合交换律,故此时 是阿贝尔群.
× ×
𝐺𝐺 (12分) 𝐺𝐺
②若群 的阶数为2,设其元素为 ,其中 是恒等元,则 ,符合交换律,故此
×
时 是 𝐺𝐺阿 贝尔群. 𝑒𝑒,𝑎𝑎 𝑒𝑒 𝑒𝑒×(𝑎𝑎1=3分𝑎𝑎×)𝑒𝑒 = 𝑎𝑎
×
③若 𝐺𝐺群 的阶数为3,设其元素为 ,其中 是恒等元,由群的封闭性, .
× ×
若 𝐺𝐺 ,又 ,推出 𝑒𝑒,𝑎𝑎,,𝑏𝑏 则集合 𝑒𝑒 有两个相同的元素,不满足集𝑎𝑎合×的𝑏𝑏 ∈唯𝐺𝐺一性 ,矛盾.所
以 𝑎𝑎×𝑏𝑏 = 𝑎𝑎 . 𝑎𝑎×𝑒𝑒 = 𝑎𝑎 𝑏𝑏 = 𝑒𝑒 𝐺𝐺
现要 𝑎𝑎验×𝑏𝑏证=交𝑒𝑒换 律,即 .事实上,若 ,有前知, 且 ,所
以 ,与群 𝑎𝑎的×封𝑏𝑏闭=性𝑏𝑏矛×盾𝑎𝑎.=所𝑒𝑒 以 𝑏𝑏×,𝑎𝑎交≠换𝑒𝑒 律成立,故𝑏𝑏此×时𝑎𝑎 ≠ 𝑎𝑎是 阿 𝑏𝑏贝×尔𝑎𝑎群≠.𝑏𝑏
× ×
𝑏𝑏 ×𝑎𝑎 ∉ 𝐺𝐺 𝑎𝑎 ×𝑏𝑏 = 𝑏𝑏×(𝑎𝑎1 5分) 𝐺𝐺
④若群 的阶数为4,设其元素为 ,其中 是恒等元,由群的封闭性, .由③的分
× ×
析可知 ,𝐺𝐺 且 ,所 𝑒𝑒以,𝑎𝑎,𝑏𝑏,𝑐𝑐 或 𝑒𝑒 . 𝑎𝑎×𝑏𝑏 ∈𝐺𝐺
若 𝑏𝑏×.𝑎𝑎由≠群𝑎𝑎 中逆 𝑏𝑏的×𝑎𝑎存≠在𝑏𝑏性 ,群 𝑎𝑎中×存𝑏𝑏 =在𝑒𝑒一 个 𝑎𝑎元×素𝑏𝑏 =使𝑐𝑐得 ,很明显 ,所以 或
×
𝑎𝑎×.𝑏𝑏假=设𝑒𝑒 ,即 ,又 𝐺𝐺 ,推出 𝑟𝑟 则 𝑟𝑟集𝑐𝑐合= 𝑒𝑒 有两个相 𝑟𝑟同≠的𝑒𝑒元 素,不 𝑟𝑟满=足𝑎𝑎 集
合 𝑟𝑟 =的唯𝑏𝑏 一性, 𝑟𝑟矛=盾𝑎𝑎. 故只 𝑎𝑎能×𝑐𝑐 = 𝑒𝑒 . 𝑎𝑎 ×𝑏𝑏 = 𝑒𝑒 𝑏𝑏 = 𝑐𝑐 𝐺𝐺
先证交换律对 成立,即 𝑎𝑎×𝑏𝑏 = 𝑐𝑐 .事实上,若 ,则由 , 只
×
能等于 .又 𝑎𝑎,𝑏𝑏 𝑎𝑎,×𝑏𝑏 = 𝑏𝑏×𝑎𝑎 ( 和 𝑏𝑏同×理𝑎𝑎 ≠),𝑎𝑎不×满𝑏𝑏 =足𝑐𝑐群 中逆的 𝑎𝑎存×在𝑏𝑏性∈,𝐺𝐺矛 盾𝑎𝑎.×所𝑏𝑏 以
𝑒𝑒 𝑐𝑐×𝑒𝑒 = 𝑐𝑐 ≠ 𝑒𝑒 𝑐𝑐×𝑏𝑏 ≠ 𝑎𝑎×𝑏𝑏 = 𝑒𝑒 𝑐𝑐 𝑎𝑎
数学参考答案 第5页(共6页)
学科网(北京)股份有限公司.交换律对 成立.
接 𝑎𝑎下×𝑏𝑏来=只𝑏𝑏需×证𝑎𝑎交=换𝑐𝑐 律对 和 𝑎𝑎,𝑏𝑏也 成立.事实上,由 和 的对称性,只需证 即可.由群中逆的
存在性,存在 𝑎𝑎使,𝑐𝑐得 𝑏𝑏,𝑐𝑐 . 𝑎𝑎 𝑏𝑏 𝑎𝑎,𝑐𝑐
(I)若 ,𝑞𝑞 ∈则{只𝑎𝑎,需𝑏𝑏}证 𝑞𝑞×𝑐𝑐 = 𝑒𝑒 .事实上,若 ,由群的封闭性,
,所 以𝑞𝑞 = 𝑎𝑎 只能等于 𝑐𝑐×,𝑎𝑎又=由𝑎𝑎前×有𝑐𝑐 = 𝑒𝑒 ,得 𝑐𝑐×𝑎𝑎 ≠ 𝑎𝑎×𝑐𝑐 = 𝑒𝑒 ,即 ,𝑐𝑐但×𝑎𝑎是∈
×
𝐺𝐺任取 的,该 𝑐𝑐结×论𝑎𝑎具 有局限性 𝑏𝑏, 不对一般的 𝑎𝑎×成𝑏𝑏立=,𝑐𝑐 故矛盾 𝑐𝑐.×即𝑎𝑎 = 𝑎𝑎×𝑏𝑏×𝑎𝑎 =,𝑏𝑏 此时交 𝑎𝑎换×律𝑎𝑎对= 1 成 立𝑎𝑎 .
(II)若 .群中逆的存在性,存在 𝑎𝑎 使得 𝑐𝑐×,𝑎𝑎又= 𝑎𝑎×𝑐𝑐 ,所以 𝑎𝑎,只𝑐𝑐 能等于
,即 𝑞𝑞 = 𝑏𝑏 ,即证 𝑝𝑝 ∈,{接𝑏𝑏,下𝑐𝑐} 来的证 𝑝𝑝法×同𝑎𝑎 =(𝑒𝑒I) ,反 𝑎𝑎证×法𝑏𝑏推=出𝑐𝑐矛≠盾𝑒𝑒 即可. 即𝑝𝑝 此时交换
律 𝑐𝑐 对 𝑎𝑎成×𝑐𝑐立=.𝑒𝑒 𝑐𝑐×𝑎𝑎 = 𝑎𝑎×𝑐𝑐 = 𝑒𝑒
故群 𝑎𝑎,𝑐𝑐 的阶数为4时,交换律成立,故此时 是阿贝尔群. (17分)
× ×
综上 所𝐺𝐺述 ,所有阶数小于等于四的群 都是阿 𝐺𝐺贝 尔群.
×
𝐺𝐺
数学参考答案 第6页(共6页)
学科网(北京)股份有限公司