新高考卷名校教研联盟2024届高三4月联考数学参考答案(1)_2024年5月_025月合集_2024届名校教研联盟高三4月联考（新高考卷）

绝密★启用前（新高考卷） 数学参考答案 1.【答案】C 9394 【解析】92，88，95，93，90，97，94，96的中位数是  93.5. 2 2．【答案】D 【解析】M {1,0,1,2,3}，N {xx1}，则∁ R N {xx≤1}，所以M ∁ R N {1,0,1}. 3.【答案】B 1 2 i 2 i 【解析】z    ，故z   . 2i 5 5 5 5 4.【答案】B 225 【解析】圆心(2,1)到直线x2y50的距离为  5 ，即圆的半径r  5，所以 1222 圆的方程为(x2)2 (y1)2 5，令 y 0，则x 0或4，故圆在x轴上的弦长为4. 5.【答案】D l 【解析】圆锥的表面积为rl r2，球的表面积为4( )2  l2，故rl r2  l2，即 2 r r r 5 1 ( )2  10，故  . l l l 2 6.【答案】A 5 5 2 【解析】由tan A ，可知sin A ，cosA ．由余弦定理有 2 3 3 BC2  AB2  AC2 2ABAC cos A9，故BC 3．设点A到边BC的距离为d ，由三 1 1 4 5 角形面积公式得： sinAABAC  BCd ，故d  ． 2 2 3 7.【答案】D 【解析】由 f(x) g(x1)可知 f(x1) g(x2)，又因为 f (x1) g(2 x)，故 g(x2) g(2x)，即g(x) g(x)，故g(x)是偶函数. 且根据题意可得 f (x) f (2 x)，故 f (x)不一定是奇函数或偶函数. 8.【答案】A 【解析】设R在线段CD，CC 上的射影分别为E，F，根据题意有PR  PE2 RE2 ， 1 QR QF2RF2 ，故EP和FQ均取最小值时，即EPBD，且FQBC时满足要求. 1 数学参考答案（新高考卷） 第1页（共8页）设REx，则RF2x， 2 2 3 3x2 故PR3QR x2( x)2 3 (2x)2( x)2  x3 4x4. 2 2 2 2 3 3x2 3 3(3x4) 设 f(x) x3 4x4，则 f(x)  ，故 f(1)0，当x[0,1) 2 2 2 3 2 x24x4 2 时， f(x)0， f(x)单调递减，当x(1,2]时， f(x)0， f(x)单调递增，故 f(x)的最 小值为 f(1)2 6，即PR3QR的最小值为2 6 . 9.【答案】AC（选对部分得3分） 【解析】甲班的平均分为90分，乙班的平均分为100分，甲班平均分低于乙班，故A正确； 甲班的方差大于乙班，但不能认为甲班的极差一定大于乙班，故B错误；甲班的平均分为 90分，乙班的平均分为100分，且乙班方差小，成绩分布更集中，故甲班成绩在区间[90,100] 的人数占比低于乙班，且低于乙班成绩在区间[100,110]的人数占比，故C正确，D错误. 10.【答案】BC（选对部分得3分） 【解析】cos76 cos104 2sin2521 2t2 1，故A错误； sin104 2sin52cos52 2t 1t2 ，故B正确； 1 cos52 1t2 tan38   ，故C正确； tan52 sin52 t 1 1t2 1cos52 1(12sin226) sin64cos26，    sin226， 2 2 2 cos26 sin64 若cos26sin226，则sin26  sin64，矛盾，故D错误. sin26 sin26 11.【答案】BCD（选对部分得3分） 【解析】设C 的半焦距为c ，离心率为e，则有 A(a,0)，B(a,b)，D(0,b)，F(c,0)， 2 OD 当AD  DF 时，由直角三角形射影定理可知 OD 2  OA  OF ， 1， OA OF DF 2 OF AD 2 AD 2  BD 2 OD 2 OA OF OF  e， 1    e，故A错误， AD 2 OA BD 2 BD 2 OA 2 OA 2 OA B正确，C正确；又 AD 2  a2 b2  c2， DF 2 b2 c2 ， AF 2 (ac)2，且 数学参考答案（新高考卷） 第2页（共8页）AD 2  DF 2  AF 2，故c2 b2 c2 (ac)2，又因为b2 c2 a2，故c2 aca2 0， 51 即e2 e10，解得e . 2 12.【答案】1 【解析】因为a (1,1)，b(2,1)，故a b  (1,2)，a(ab)1(1)1(2)1. 3 2 13.【答案】 2 【解析】设 A(x ,y )，B(x ,y )，根据题意可知y  y ，故2x 4x ，即x  2x ，又 1 1 2 2 1 2 1 2 1 2 1 1 由抛物线的定义可知 AF  x  ，BF x 1，当 AF  BF 时，x   x 1， 1 1 2 2 2 1 2 1 2 2 1 3 故x 1，x  ，y  y  2 ，所以|FF || AB| ，四边形ABF F 是平行四边形， 1 2 2 1 2 1 2 2 2 1 3 2 故四边形ABF F 的面积为 y  AB  y  x x  . 2 1 1 1 1 2 2 1 3 14.【答案】( , )(2,) 2 2 【解析】 f(x)6x2 6x，令 f(x)0，则x0或x1，当x0或x1时， f(x)0， f(x)单调递增，当0 x1时，f(x)0，f(x)单调递减，所以 f(x)的极大值是 f(0)3， 极小值是 f(1)2．当x1时，f(x) f(x) 2；令 f(x)2，即2x33x210，因为x1 1 1 是极小值点，设存在x 使得2x33x212(x1)2(xx )0，解得x  ，故当 x1 0 0 0 2 2 1 时，f(x) f(x) 2；易知 f(1)2，故当x1时，f(x)2，f(x) 2，且当1x 2 时， f(x) 2．结合 f(x)的图像可知，对于任意x，若 f(x) ， f(xk) 二者中至少有一 1 3 1 3 个大于2，则 k  或k 2，即k 的取值范围是( , )(2,)． 2 2 2 2 15.（13分） c 3 【解析】（1）设C 的半焦距为c，则  ． ……1分 a 3 2a2 故b2 a2 c2  ． ……3分 3 2 3 1 4 3 将P(1, )代入C 的方程有  1，故 1，a2 3，b2 2． 3 a2 3b2 a2 x2 y2 所以C 的方程为  1. ……5分 3 2 数学参考答案（新高考卷） 第3页（共8页）（2）由（1）可知C 的左焦点为(1,0). ……6分 故过左焦点且斜率为 2 的直线为l:y 2x 2. ……7分 将l与C 的方程联立有2x23x0. ……8分 3 设M(x,y )，N(x ,y )，则不妨取x 0，x  . ……9分 1 1 2 2 1 2 2 3 3 故 MN  3x x  . ……10分 1 2 2 2 3 2  2 3 2 62 且P到l的距离d   . ……11分 21 3 MN d 1 3 3 2 62 3 2 3 所以△PMN 的面积为     . 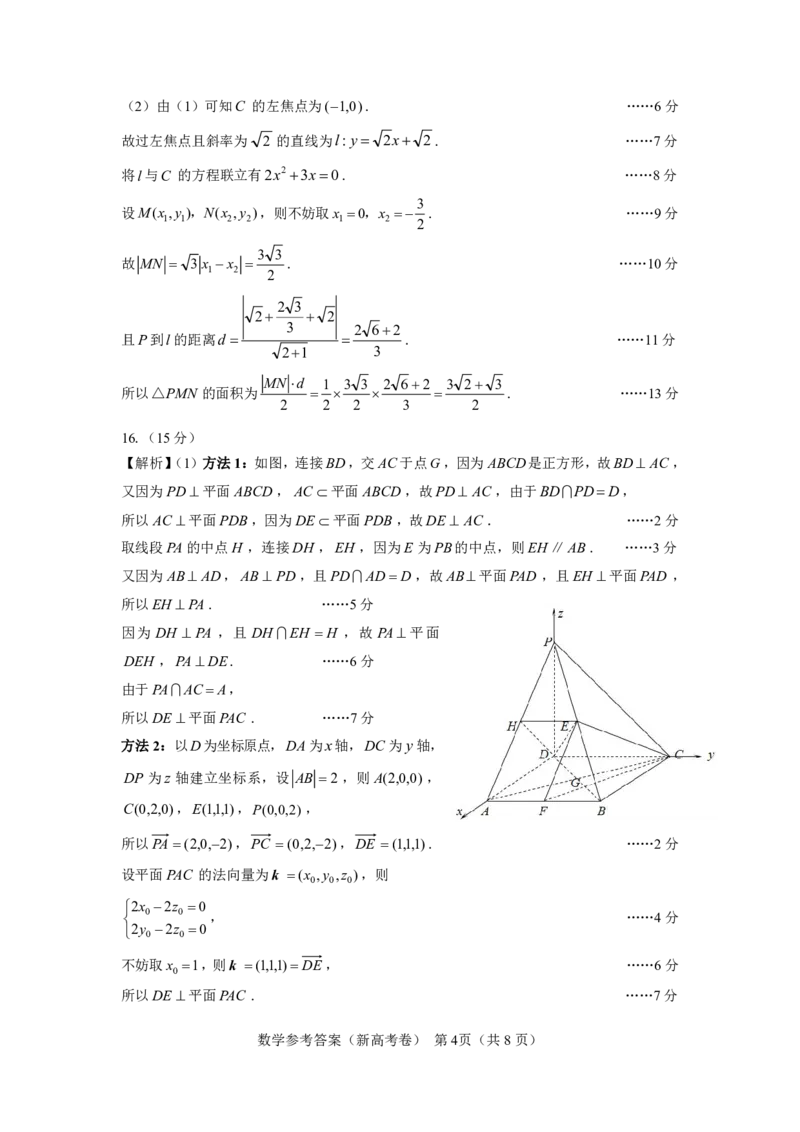……13分 2 2 2 3 2 16.（15分） 【解析】（1）方法1：如图，连接BD，交AC于点G，因为ABCD是正方形，故BD AC， 又因为PD平面ABCD，AC平面ABCD，故PD AC，由于BDPDD， 所以AC 平面PDB，因为DE平面PDB，故DE  AC． ……2分 取线段PA的中点H ，连接DH ，EH ，因为E 为PB的中点，则EH∥AB. ……3分 又因为AB AD，ABPD，且PDADD，故AB平面PAD ，且EH 平面PAD ， 所以EH PA. ……5分 因为 DH PA ，且 DH EH H ，故 PA平面 DEH ，PADE. ……6分 由于PAACA， 所以DE 平面PAC . ……7分 方法2：以D为坐标原点，DA为x轴，DC为y轴， DP为z 轴建立坐标系，设 AB 2 ，则A(2,0,0) ， C(0,2,0)，E(1,1,1)，P(0,0,2)， 所以PA (2,0,2)，PC (0,2,2)，DE (1,1,1). ……2分 设平面PAC 的法向量为k (x ,y ,z )，则 0 0 0 2x 2z 0  0 0 ， ……4分 2y 2z 0 0 0 不妨取x 1，则k (1,1,1)DE， ……6分 0 所以DE 平面PAC . ……7分 数学参考答案（新高考卷） 第4页（共8页）（2）以D为坐标原点，DA为x轴，DC为y轴，DP为z轴建立坐标系，设 AB 2，则B(2,2,0)， C(0,2,0)，E(1,1,1)，F(2,1,0)， 所以BC (2,0,0)，CE (1,1,1)，FC (2,1,0). ……10分 设平面BCE 与平面CEF的法向量分别为m (x ,y ,z )，n (x ,y ,z )，则 1 1 1 2 2 2 2x 0 2x  y 0  1 ， 2 2 ， x y z 0 x y z 0 1 1 1 2 2 2 不妨取y 1，x 1，则m (0,1,1)，n (1,2,1)， ……13分 1 2 mn 3 所以cos m,n   ， ……14分 m n 2 因为 m,n [0,180]，故二面角BCE F 的大小为30. ……15分 17.（15分） 【解析】（1）根据题意有X 0,1,2， C2 28 C1 C1 16 C2 1 则P(X 0) 8  ，P(X 1)  2 8  ，P(X2) 2  . ……3分 C2 45 C2 45 C2 45 10 10 10 X 的分布列为： X 0 1 2 28 16 1 ……5分 P 45 45 45 28 16 1 2 所以EX 0 1 2  . ……8分 45 45 45 5 C2 (n2)(n3) 4n6 （2）当有n个小球时，顾客中奖概率为P1 n2 1  . ……12分 C2 n(n1) n(n1) n 4n6 1 故P≥25%，即 ≥ . ……13分 n(n1) 4 17 193 解得n≤ ，满足条件的n的最大值为15. 2 所以若使中奖概率不低于25%，则n的最大值为15. ……15分 18.（17分） 【解析】（1）若{a }对{b }关于0耦合，则a b ，且b a ， n n n1 n n1 n 所以a b a ，b a b ， ……1分 n2 n1 n n2 n1 n 因为a 1，b 2， 1 1 数学参考答案（新高考卷） 第5页（共8页）1，n为奇数 2，n为奇数 故a  ，b  . ……3分 n 2，n为偶数 n 1，n为偶数 a a2 a2n 1 1 1 所以 1  2  2n  22 24 22n ……4分 b b2 b2n 2 23 22n1 1 2 2n 1 1 1 2 1 (   )(22 24 22n) (24n  1). ……6分 2 23 22n1 3 4n （2）若{a }对{b }关于1耦合，则a b 1，且b 2a ， n n n1 n n1 n 所以a b 12a 1，b 2a 2b 2，故a 12(a 1)， ……7分 n2 n1 n n2 n1 n n2 n 又因为a b 1，故a b 12， 1 1 2 1 n1 n1 故当n为奇数时，a 1(a 1)2 2 ，即a 2 2 1， ……8分 n 1 n n2 所以当n为偶数时，b a 12 2 2； ……9分 n n1 n2 n2 当n为偶数时，a 1(a 1)2 2 ，即a 32 2 1， ……10分 n 2 n n1 所以当n为奇数时，b a 132 2 2. ……11分 n n1  n1  n1 2 2 1，n为奇数 32 2 2，n为奇数 综上，a  ，b  . ……12分 n n2 n n2   32 2 1，n为偶数 2 2 2，n为偶数 （3）由题设可知，a b  p ，b (p 1)a ，且a2 b2 p ，b2 (p 1)a2. n1 n 1 n1 1 n n1 n 2 n1 2 n （i）若p 0，则a b ，b a ，a2 b2，b2 a2，显然p 0. ……13分 1 n1 n n1 n n1 n n1 n 2 p  p2 （ii）若p 0，由上得a2 (b  p )2 b22pb  p2 b2 p ，故b  2 1 . 1 n1 n 1 n 1 n 1 n 2 n 2p 1 假设 p  p2，则b 0，b (p 1)a 0，故p 1或a 0. ……14分 2 1 n n1 1 n 1 n ①若p 1，则 p  p2 1，a b  p 1，b2 (p 1)a2 2，这与b 0矛盾； 1 2 1 n1 n 1 n2 2 n1 n ②若a 0，则a 0， p a b 0，这与 p 0矛盾. n n1 1 n1 n 1 p  p2 所以若p 0，则p  p2，b  2 1 0. ……15分 1 2 1 n 2p 1 p p2 故b2 (p 1)a2(p 1)2a20，可得p p22p ，故b  2 1 1. ……16分 n1 2 n 1 n 2 1 1 n 2p 1 所以对于任意nN*，a b  p 1 p ，且b (p 1)a (p 1)2 1，由于 p 0， n1 n 1 1 n2 1 n1 1 1 故 p 2， p  p22p 0，代入题设检验，各式均成立. 1 2 1 1 综上，p ,p {2,0}. ……17分 1 2 数学参考答案（新高考卷） 第6页（共8页）19.（17分） 【解析】（1）设N(x ,y )，则根据题意有 x2  y2 5. ……1分 N N N N 因为N ~ M ，则存在点W(x ,y )，使得： W W (x ,y )  (y ,x )(1,2)(x ,y )  (x y ,2x y ). ……2分 N N W W W W W W W W 由条件知x y 0，由 N 5得 (x y )2 (2x y )2 5 ，解得x y  5， W W W W W W W W 所以N 的坐标为( 5,2 5)，N的坐标为(2 5, 5). ……3分 故M N的坐标为(2,1)(2 5, 5)(4 5, 5). ……4分 （2）由条件知点(x ,*(x ))在函数*(x)图像上，则点(*(x ),x )在函数*(x)的镜像函数 A A A A (x)图像上. ……5分 ((x )) x 所以(*(x )) x ．同理*((x )) x ，即 A  A . ……7分 A A B B ((x )) x B B x A ((x )) A 由（1）可知，若A~ B ，则 A  ，故 A  . ……8分 x B ((x )) B B B （3）设R(x ,y )，若R~S，且 R  S ，由（1）可知，存在0k1使得S(kx ,ky ) . 0 0 0 0 故 R  x2  y2 ， S  k x2  y2 ，且 2 RS  2kx y ≤ k(x2  y2) ，故若 0 0 0 0 0 0 0 0 f( R )f( S ) 2 RS ，只需 f( x2y2)f(k x2y2)k(x2y2)（*）.……10分 0 0 0 0 0 0 由（2）可知 f (f (x))  f (f (x))  x ，且因为 f(x)， f(x)的定义域均为(0,)，由对 称性可知 f (x)，f(x)的值域也均为(0,). ……11分 f( x2  y2) k x2  y2 f(f(k x2  y2)) 故（*）等价于 0 0  0 0  0 0 . ……12分 x2  y2 f(k x2  y2) f(k x2  y2) 0 0 0 0 0 0 f (x) ex  x2 1 (x1)ex  x2 1 设g(x)  ，则g(x) . ……13分 x x x2 设h(x)(x1)ex  x2 1，则h(x) xex 2x ，当x 0 时，h(x) 0，h(x)单调递增， h(x) 故当x 0 时，h(x) h(0)0 ，g(x)  0，g(x)单调递增. ……14分 x2 设t(x) f(x)x ex  x2 x1，则t(x)ex 2x1，当x 0 时，t(x) 0，t(x) 单 数学参考答案（新高考卷） 第7页（共8页）调递增，故t(x)t(0)0，即 f (x) x，且由对称性可知0 f(x) x. ……15分 所以0 f(k x2y2)k x2y2  x2y2 ，故g( x2 y2) g(f(k x2 y2)). 0 0 0 0 0 0 0 0 0 0 综上， f( R )f( S ) 2 RS . ……17分 数学参考答案（新高考卷） 第8页（共8页）