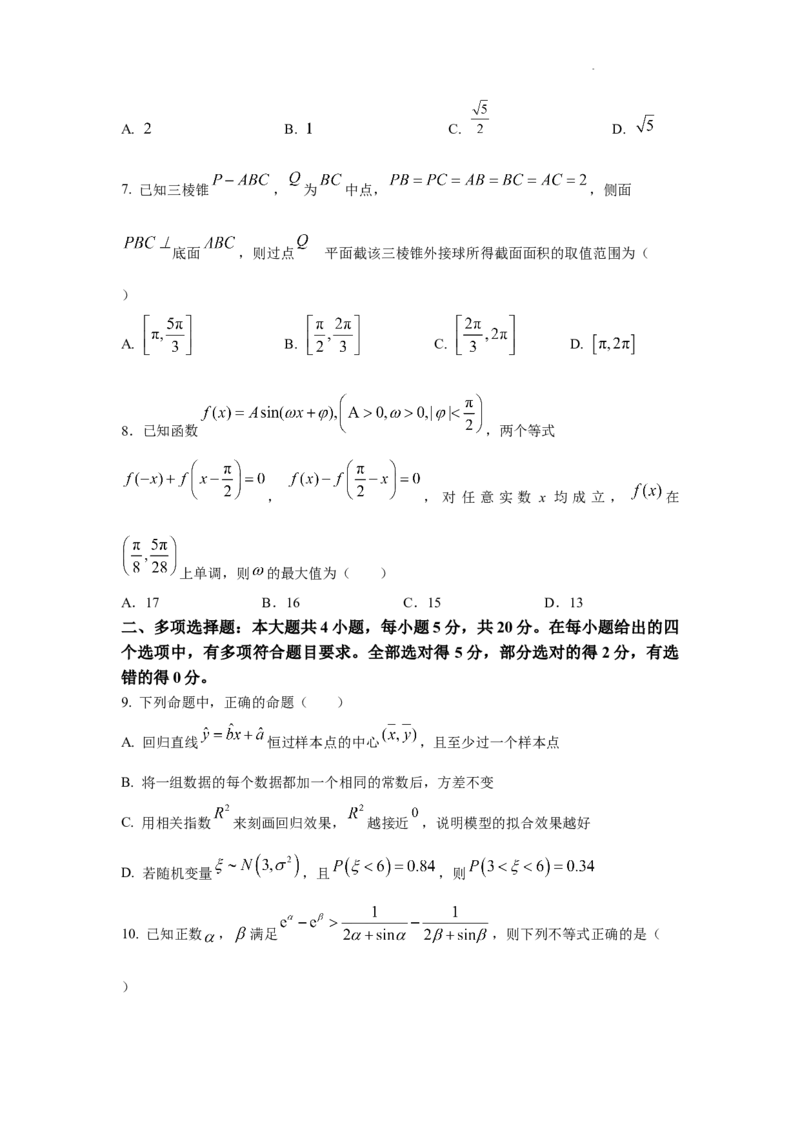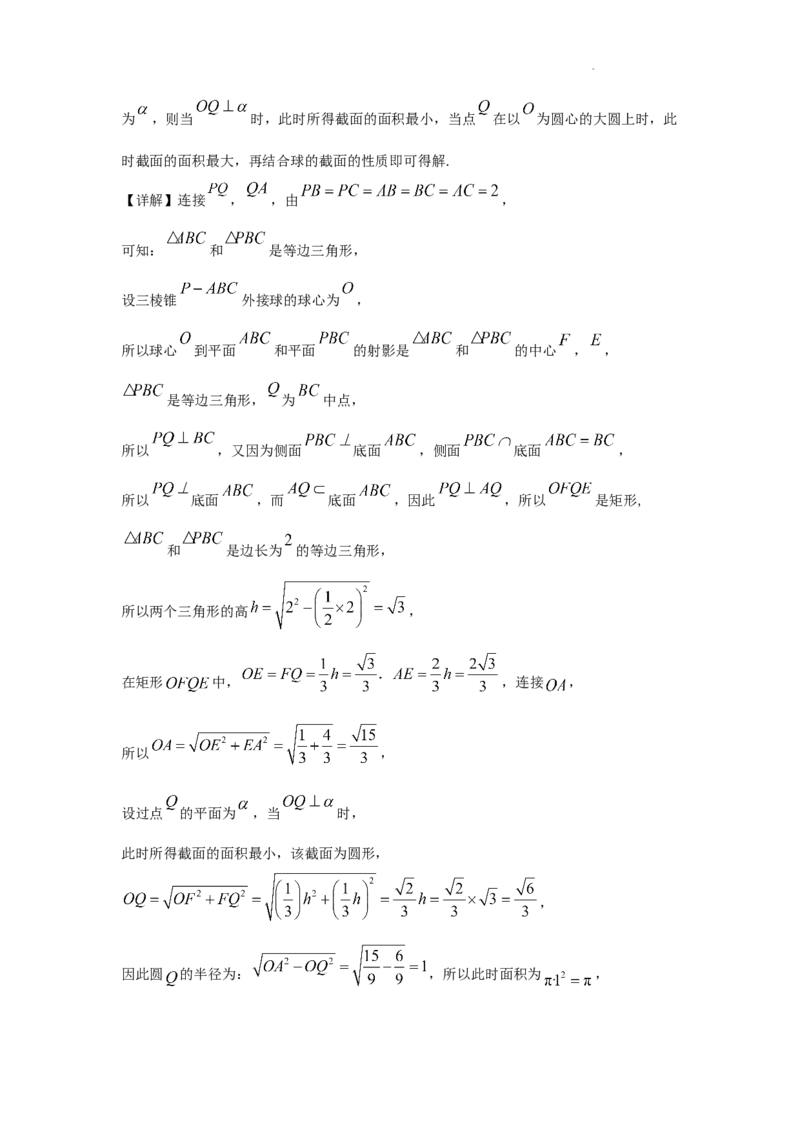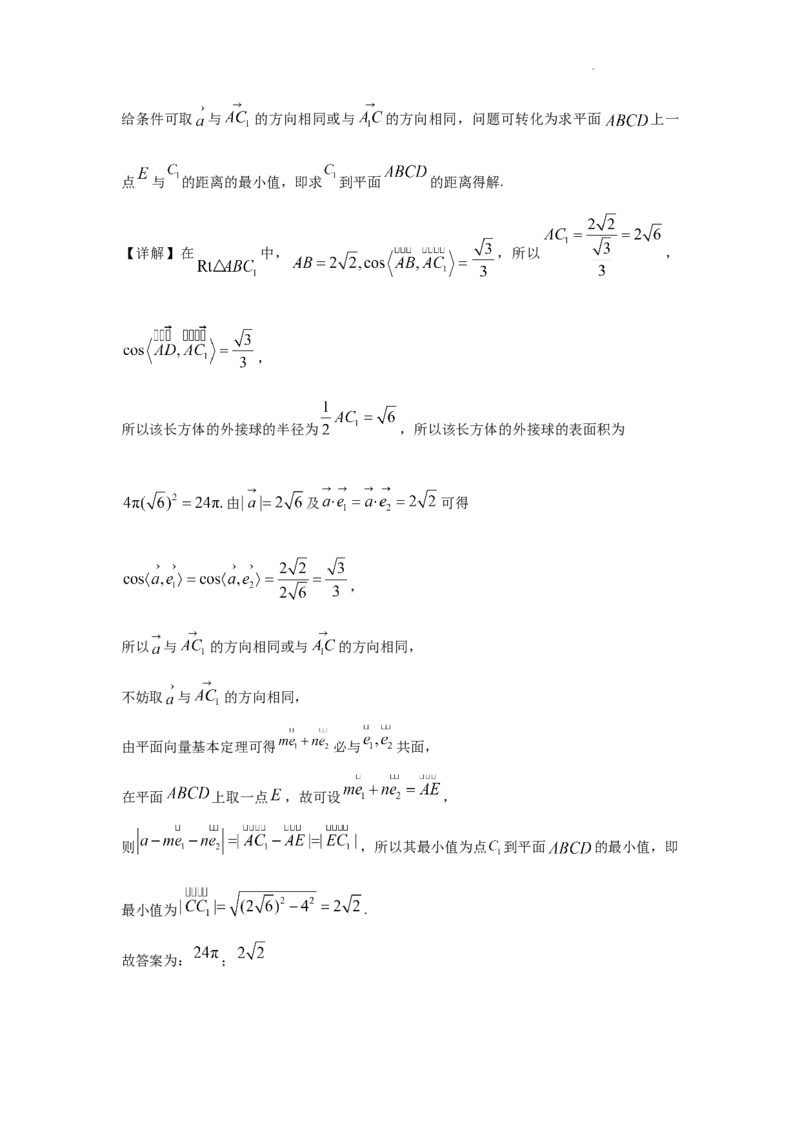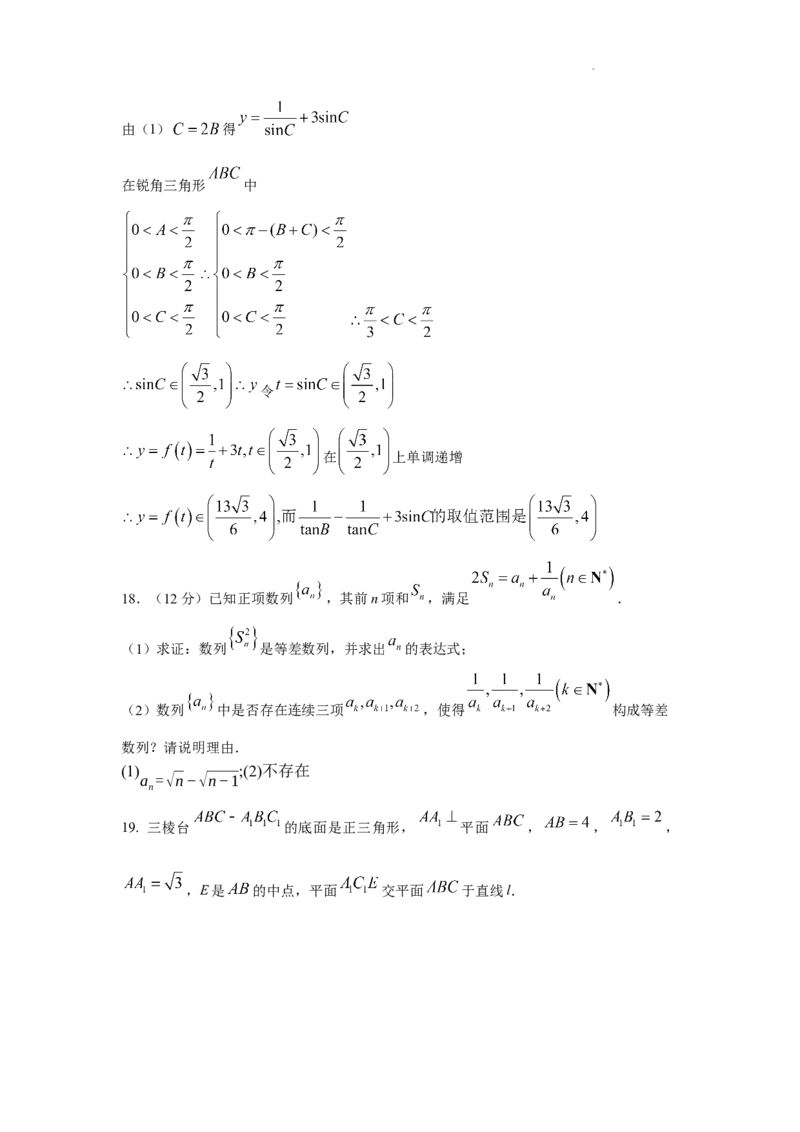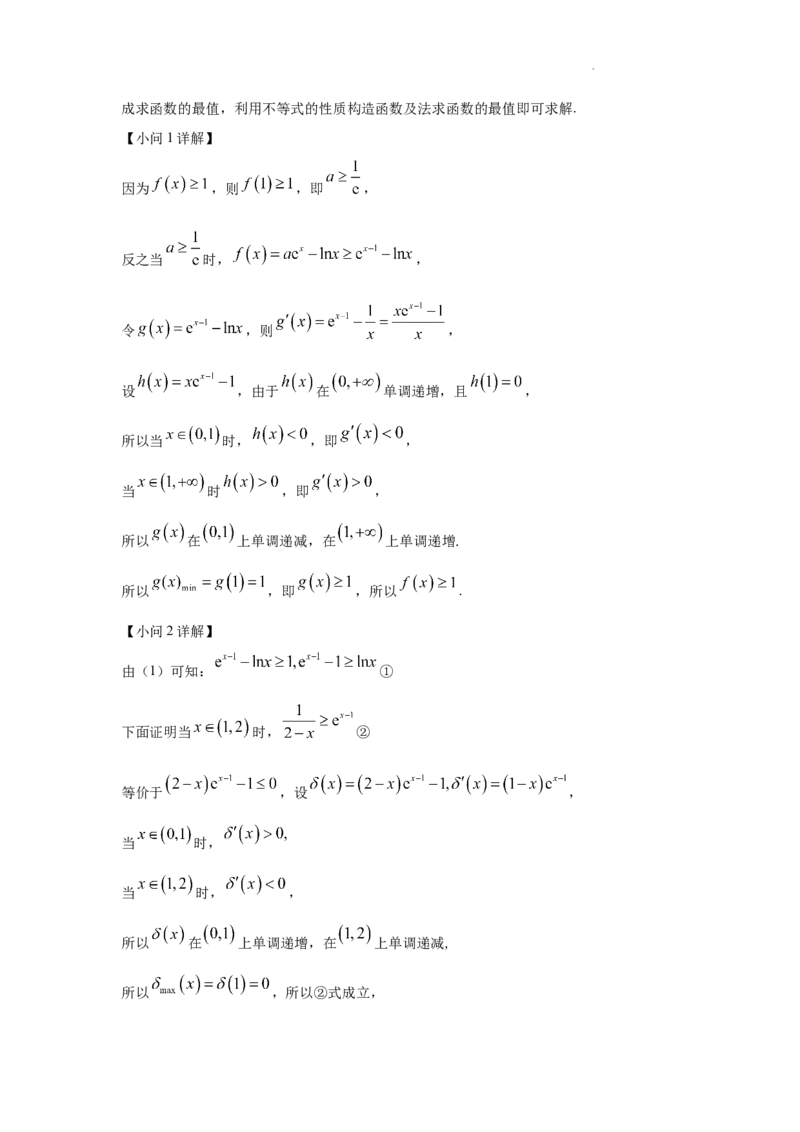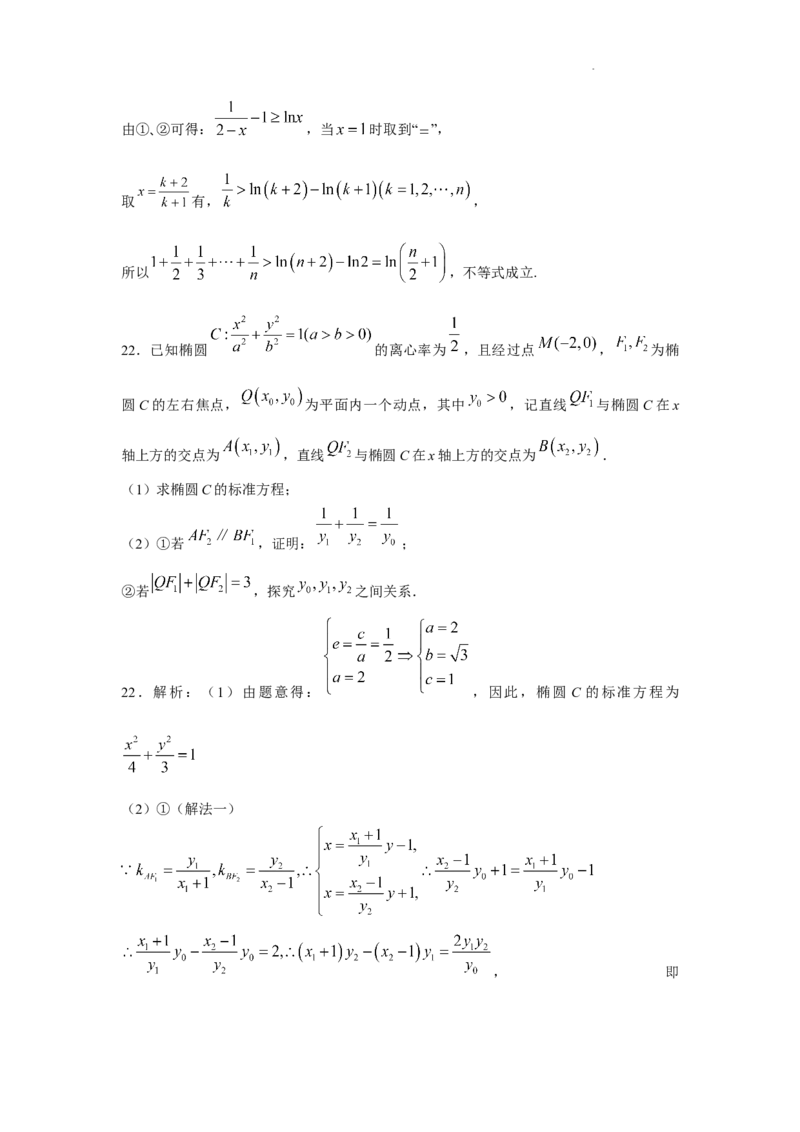文档内容
江苏省扬州中学 2022-2023 学年度
高三数学双周练试卷
2023.3.1
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个
选项中,只有一项是符合题目要求的.
1. 已知复数: ,则z在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 设P(A|B)=P(B|A)= ,P(A)= ,则P(B)等于( )
A. B. C. D.
3.下列说法正确的是( )
A.“ ”是“ ”的充要条件
B.“ ”是“ ”的必要不充分条件
C.命题“ ”的否定形式是“ ”
D.“ ”是“ ”的充分不必要条件
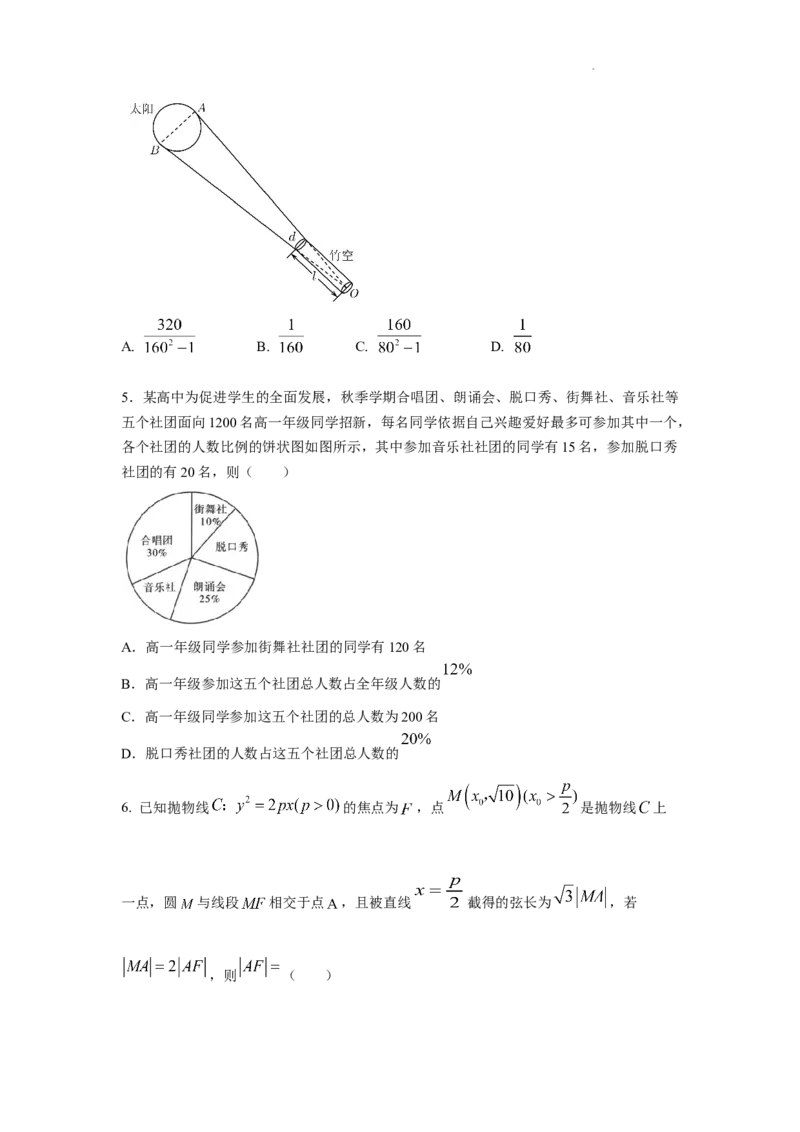
4. 《周髀算经》中“侧影探日行”一文有记载:“即取竹空,径一寸,长八尺,捕影而视之,
空正掩目,而日应空之孔.”意谓:“取竹空这一望筒,当望筒直径d是一寸,筒长l是八尺
时(注:一尺等于十寸),从筒中搜捕太阳的边缘观察,则筒的内孔正好覆盖太阳,而太
阳的外缘恰好填满竹管的内孔.”如图所示,O为竹空底面圆心,则太阳角∠AOB的正切值
为( )
学科网(北京)股份有限公司A. B. C. D.
5.某高中为促进学生的全面发展,秋季学期合唱团、朗诵会、脱口秀、街舞社、音乐社等
五个社团面向1200名高一年级同学招新,每名同学依据自己兴趣爱好最多可参加其中一个,
各个社团的人数比例的饼状图如图所示,其中参加音乐社社团的同学有15名,参加脱口秀
社团的有20名,则( )
A.高一年级同学参加街舞社社团的同学有120名
B.高一年级参加这五个社团总人数占全年级人数的
C.高一年级同学参加这五个社团的总人数为200名
D.脱口秀社团的人数占这五个社团总人数的
6. 已知抛物线 的焦点为 ,点 是抛物线 上
一点,圆 与线段 相交于点 ,且被直线 截得的弦长为 ,若
,则 ( )
学科网(北京)股份有限公司A. B. C. D.
7. 已知三棱锥 , 为 中点, ,侧面
的
底面 ,则过点 平面截该三棱锥外接球所得截面面积的取值范围为(
)
A. B. C. D.
8.已知函数 ,两个等式
, , 对 任 意 实 数 x 均 成 立 , 在
上单调,则 的最大值为( )
A.17 B.16 C.15 D.13
二、多项选择题:本大题共4小题,每小题5分,共20分。在每小题给出的四
个选项中,有多项符合题目要求。全部选对得 5分,部分选对的得 2分,有选
错的得0分。
9. 下列命题中,正确的命题( )
A. 回归直线 恒过样本点的中心 ,且至少过一个样本点
B. 将一组数据的每个数据都加一个相同的常数后,方差不变
C. 用相关指数 来刻画回归效果, 越接近 ,说明模型的拟合效果越好
D. 若随机变量 ,且 ,则
10. 已知正数 , 满足 ,则下列不等式正确的是(
)
学科网(北京)股份有限公司1 1 4
A. + > B.
α β α+β
C. D.
11.折纸是一种高雅的艺术活动.已知正方形纸片 的边长为2,现将 沿对角线
旋转 ,记旋转过程中点 的位置为点 中点分别为 ,则(
)
A.
B. 最大为
C.旋转过程中, 与平面BOP所成的角不变
D. 旋转形成的几何体的体积是
12. 在平面四边形ABCD中, 的面积是 面积的2倍,又数列 满足
,恒有 ,设 的前n项和为 ,则(
)
A. 为等比数列 B. 为等差数列
C. 为递增数列 D.
非选择题部分(共90分)
三、填空题:本大题共4小题,每小题5分,共20分。
13. 在 的二项式展开式中 的系数为90,则 ______.
14. 已知双曲线 ,若过点 能做该双曲线的两条切线,则该双曲线离心率
学科网(北京)股份有限公司取值范围为______.
15. 在平面直角坐标系 中,已知圆 , ,直线 与圆
相切,与圆 相交于 , 两点,分别以点 , 为切点作圆 的切线 , 设直线 ,
的交点为 ,则 的最大值为__________.
16. 已 知 长 方 体 的 底 面 是 边 长 为 的 正 方 形 , 若
,则该长方体的外接球的表面积为________;记 分别是
方向上的单位向量,且 , ,则 (m,
n为常数)的最小值为________.
四、解答题:本题共6小题,共70分.解答应写出相应的文宇说明、证明过程或演
算步骤.
17.(12分)在锐角 中,角 所对的边分别是 ,满足 .
(1)求证: ;
(2)求 的取值范围.
18.(12分)已知正项数列 ,其前n项和 ,满足 .
(1)求证:数列 是等差数列,并求出 的表达式;
学科网(北京)股份有限公司(2)数列 中是否存在连续三项 ,使得 构成等差
数列?请说明理由.
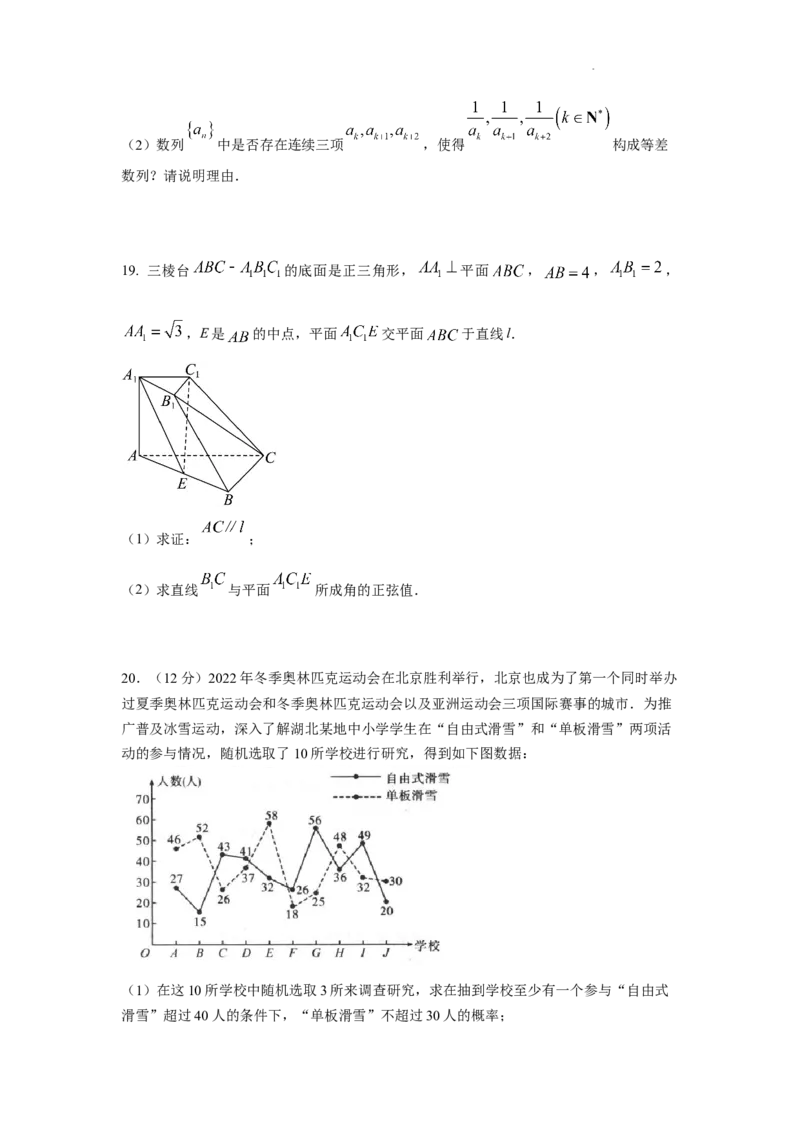
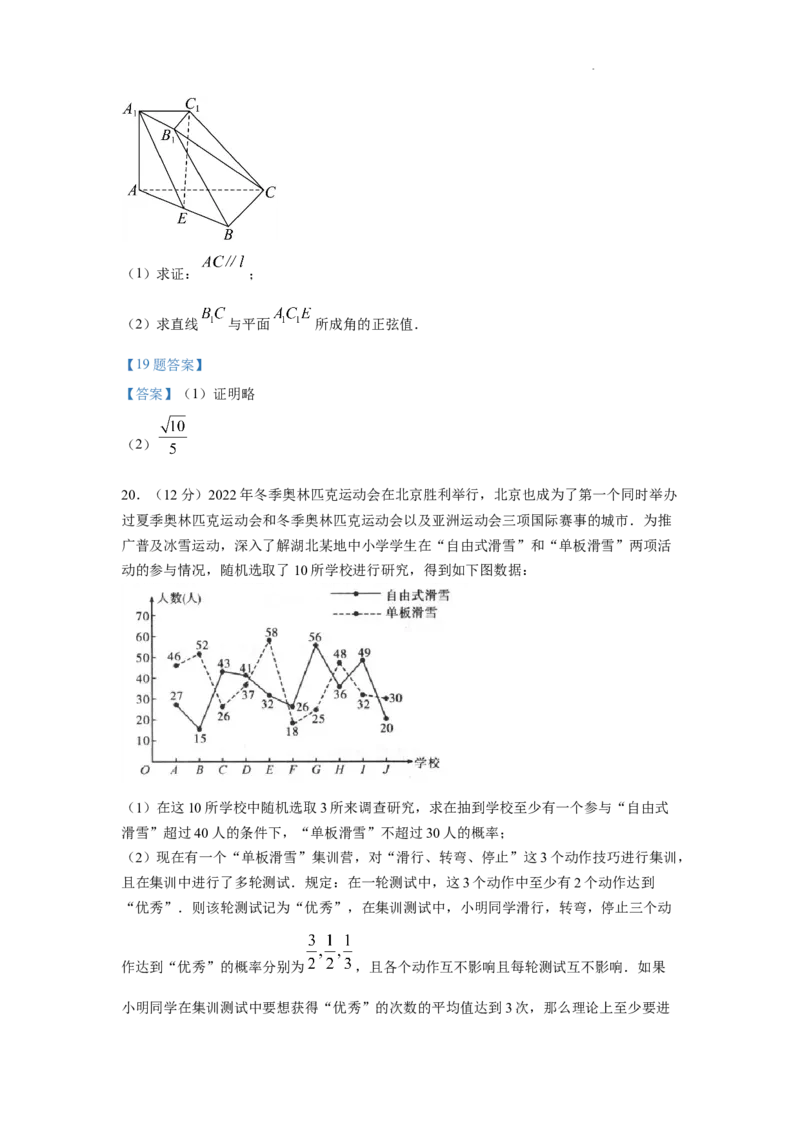
19. 三棱台 的底面是正三角形, 平面 , , ,
,E是 的中点,平面 交平面 于直线l.
(1)求证: ;
(2)求直线 与平面 所成角的正弦值.
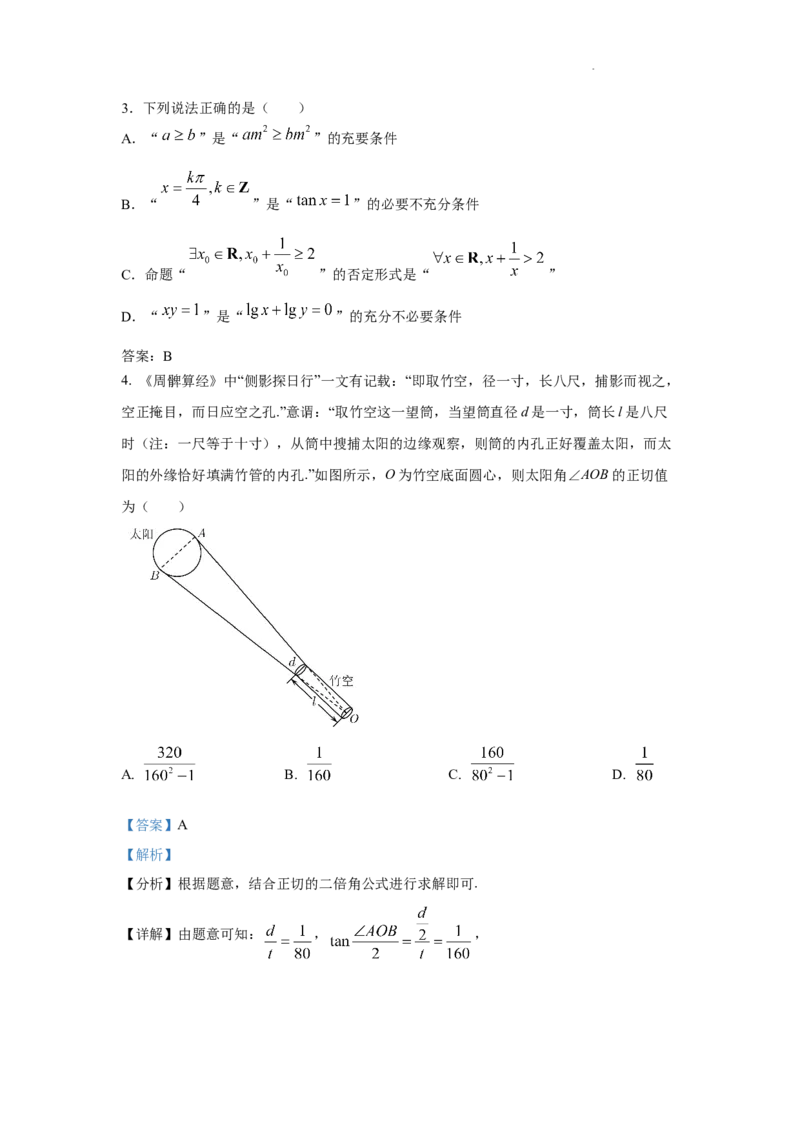
20.(12分)2022年冬季奥林匹克运动会在北京胜利举行,北京也成为了第一个同时举办
过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市.为推
广普及冰雪运动,深入了解湖北某地中小学学生在“自由式滑雪”和“单板滑雪”两项活
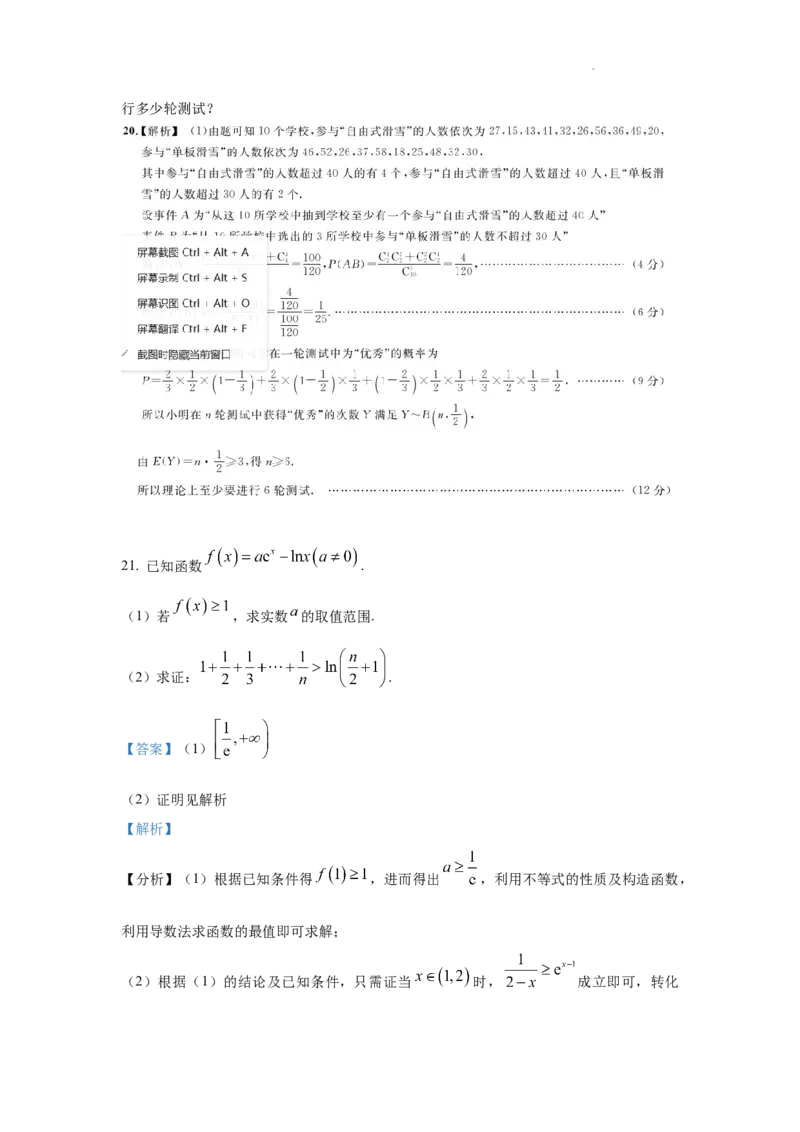
动的参与情况,随机选取了10所学校进行研究,得到如下图数据:
(1)在这10所学校中随机选取3所来调查研究,求在抽到学校至少有一个参与“自由式
滑雪”超过40人的条件下,“单板滑雪”不超过30人的概率;
学科网(北京)股份有限公司(2)现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这3个动作技巧进行集训,
且在集训中进行了多轮测试.规定:在一轮测试中,这3个动作中至少有2个动作达到
“优秀”.则该轮测试记为“优秀”,在集训测试中,小明同学滑行,转弯,停止三个动
作达到“优秀”的概率分别为 ,且各个动作互不影响且每轮测试互不影响.如果
小明同学在集训测试中要想获得“优秀”的次数的平均值达到3次,那么理论上至少要进
行多少轮测试?
21. 已知函数 .
(1)若 ,求实数 的取值范围.
(2)求证: .
22.已知椭圆 的离心率为 ,且经过点 , 为椭
圆C的左右焦点, 为平面内一个动点,其中 ,记直线 与椭圆C在x
轴上方的交点为 ,直线 与椭圆C在x轴上方的交点为 .
(1)求椭圆C的标准方程;
(2)①若 ,证明: ;
②若 ,探究 之间关系.
学科网(北京)股份有限公司江苏省扬州中学高三数学双周练试卷
2023.3.1
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个
选项中,只有一项是符合题目要求的.
1. 已知复数: ,则z在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】B
【解析】
【分析】对复数z进行化简,从而求出其所在的象限即可.
【详解】 ,
故z在复平面内对应的点位于第二象限,
故选B.
【点睛】本题考查了复数的运算,考查复数的几何意义,是一道基础题.
2. 设P(A|B)=P(B|A)= ,P(A)= ,则P(B)等于( )
A. B. C. D.
【答案】B
【解析】
【分析】由已知可求出 ,再由 即可求出.
【详解】 ,
由 ,得 .
故选:B.
学科网(北京)股份有限公司3.下列说法正确的是( )
A.“ ”是“ ”的充要条件
B.“ ”是“ ”的必要不充分条件
C.命题“ ”的否定形式是“ ”
D.“ ”是“ ”的充分不必要条件
答案:B
4. 《周髀算经》中“侧影探日行”一文有记载:“即取竹空,径一寸,长八尺,捕影而视之,
空正掩目,而日应空之孔.”意谓:“取竹空这一望筒,当望筒直径d是一寸,筒长l是八尺
时(注:一尺等于十寸),从筒中搜捕太阳的边缘观察,则筒的内孔正好覆盖太阳,而太
阳的外缘恰好填满竹管的内孔.”如图所示,O为竹空底面圆心,则太阳角∠AOB的正切值
为( )
A. B. C. D.
【答案】A
【解析】
【分析】根据题意,结合正切的二倍角公式进行求解即可.
【详解】由题意可知: , ,
学科网(北京)股份有限公司所以 .
故选:A.
5.某高中为促进学生的全面发展,秋季学期合唱团、朗诵会、脱口秀、街舞社、音乐社等
五个社团面向1200名高一年级同学招新,每名同学依据自己兴趣爱好最多可参加其中一个,
各个社团的人数比例的饼状图如图所示,其中参加音乐社社团的同学有15名,参加脱口秀
社团的有20名,则( )
A.高一年级同学参加街舞社社团的同学有120名
B.高一年级参加这五个社团总人数占全年级人数的
C.高一年级同学参加这五个社团的总人数为200名
D.脱口秀社团的人数占这五个社团总人数的
答案:D
6. 已知抛物线 的焦点为 ,点 是抛物线 上
一点,圆 与线段 相交于点 ,且被直线 截得的弦长为 ,若
,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】根据点在抛物线上及抛物线的定义,利用圆的弦长及勾股定理即可求解
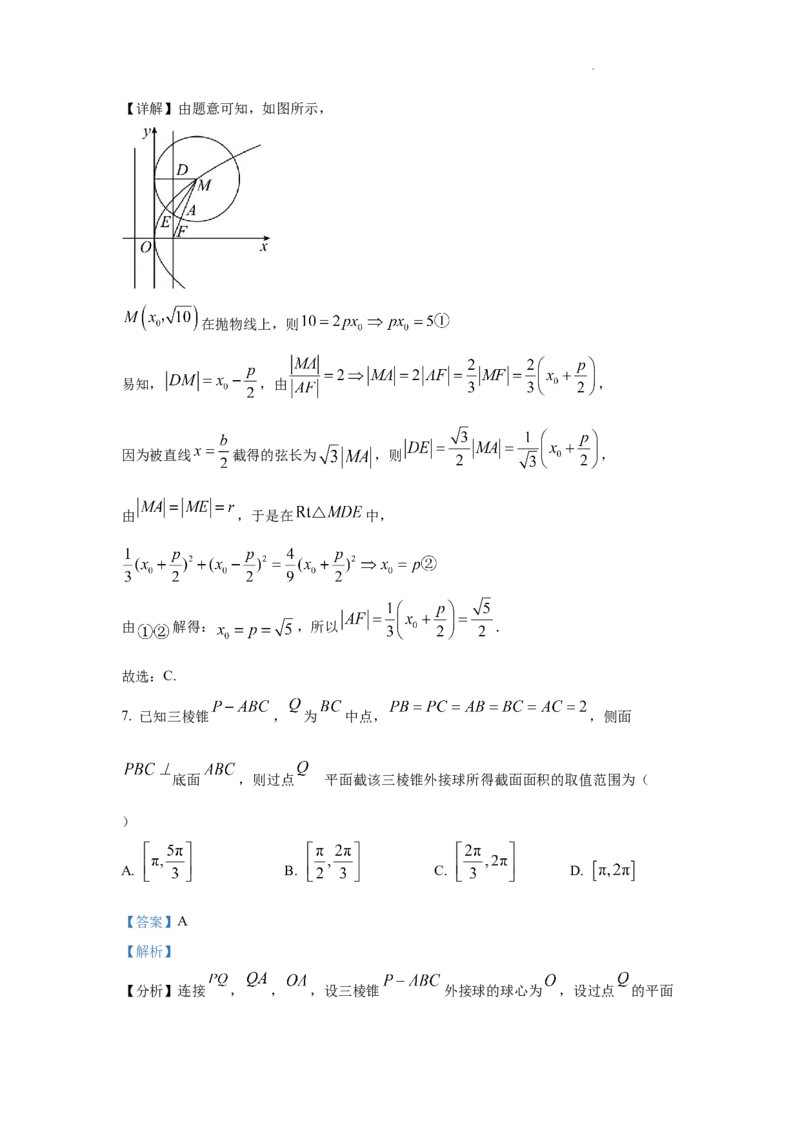
学科网(北京)股份有限公司【详解】由题意可知,如图所示,
在抛物线上,则
易知, ,由 ,
因为被直线 截得的弦长为 ,则 ,
由 ,于是在 中,
由 解得: ,所以 .
故选:C.
7. 已知三棱锥 , 为 中点, ,侧面
的
底面 ,则过点 平面截该三棱锥外接球所得截面面积的取值范围为(
)
A. B. C. D.
【答案】A
【解析】
【分析】连接 , , ,设三棱锥 外接球的球心为 ,设过点 的平面
学科网(北京)股份有限公司为 ,则当 时,此时所得截面的面积最小,当点 在以 为圆心的大圆上时,此
时截面的面积最大,再结合球的截面的性质即可得解.
【详解】连接 , ,由 ,
可知: 和 是等边三角形,
设三棱锥 外接球的球心为 ,
所以球心 到平面 和平面 的射影是 和 的中心 , ,
是等边三角形, 为 中点,
所以 ,又因为侧面 底面 ,侧面 底面 ,
所以 底面 ,而 底面 ,因此 ,所以 是矩形,
和 是边长为 的等边三角形,
所以两个三角形的高 ,
在矩形 中, ,连接 ,
所以 ,
设过点 的平面为 ,当 时,
此时所得截面的面积最小,该截面为圆形,
,
因此圆 的半径为: ,所以此时面积为 ,
学科网(北京)股份有限公司当点 在以 为圆心的大圆上时,此时截面的面积最大,面积为: ,
所以截面的面积范围为 .
故选:A.
8.已知函数 ,两个等式
, , 对 任 意 实 数 x 均 成 立 , 在
上单调,则 的最大值为( )
A.17 B.16 C.15 D.13
8.解析: , , 的一个对称中心
为
, 的对称轴方程 ,
学科网(北京)股份有限公司在 上 单 调 ,
,故选C.
二、多项选择题:本大题共4小题,每小题5分,共20分。在每小题给出的四
个选项中,有多项符合题目要求。全部选对得 5分,部分选对的得 2分,有选
错的得0分。
9. 下列命题中,正确的命题( )
A. 回归直线 恒过样本点的中心 ,且至少过一个样本点
B. 将一组数据的每个数据都加一个相同的常数后,方差不变
C. 用相关指数 来刻画回归效果, 越接近 ,说明模型的拟合效果越好
D. 若随机变量 ,且 ,则
【答案】BD
【解析】
【分析】对于A,利用回归直线的性质即可判断;
对于B,利用方差的性质即可判断;
对于C,利用相关指数 的性质即可判断;
对于D,利用正态分布的对称性即可求解.
【详解】对于A,回归直线 恒过样本点的中心 ,不一定过样本点,故A
错误;
对于B,将一组数据的每个数据都加一个相同的常数后,数据的波动性不变,故方差不变,
故B正确;
对于C,用相关指数 来刻画回归效果, 越接近 ,说明模型的拟合效果越好,故C
错误;
对于D,因为随机变量 ,所以
学科网(北京)股份有限公司,故D正确.
故选:BD.
10. 已知正数 , 满足 ,则下列不等式正确的是(
)
1 1 4
A. + > B.
α β α+β
C. D.
【答案】ABD
【解析】
【分析】构造函数 ,利用导数得出 ,由基本不等式判断
A;由指数和对数的单调性以及不等式的性质判断BCD.
【详解】解:因为正数 , 满足 ,
所以 ,构造函数 , ,
令 , 恒成立,所以 在 上单调递增,
由复合函数的单调性可知 在 上单调递增,
所以 在 上单调递增,由 ,可得 ,
对于A, ,所以 ,故A
正确
学科网(北京)股份有限公司对于B,由 ,可得 ,所以 ,故B正确
对于C,由 ,可得 ,则 ,故C错误
对于D,由 ,可得 , ,所以 ,所以
,故D正确.
故选:BD.
11.折纸是一种高雅的艺术活动.已知正方形纸片 的边长为2,现将 沿对角线
旋转 ,记旋转过程中点 的位置为点 中点分别为 ,则(
)
A.
B. 最大为
C.旋转过程中, 与平面BOP所成的角不变
D. 旋转形成的几何体的体积是
答案:AD
12. 在平面四边形ABCD中, 的面积是 面积的2倍,又数列 满足
,恒有 ,设 的前n项和为 ,则(
)
A. 为等比数列 B. 为等差数列
C. 为递增数列 D.
【答案】BD
学科网(北京)股份有限公司非选择题部分(共90分)
三、填空题:本大题共4小题,每小题5分,共20分。
13. 在 的二项式展开式中 的系数为90,则 ______.
【答案】
【解析】
【分析】利用展开式的通项 ,令 求出 ,进而求解.
【详解】因为 的二项式展开式的通项为
,
令 ,解得: ,所以 ,
又因为 的二项式展开式中 的系数为90,则 ,
所以 ,
故答案为: .
14. 已知双曲线 ,若过点 能做该双曲线的两条切线,则该双曲线离心率
取值范围为______.
【答案】
【解答】解:过 能作两条切线说明该点在双曲线外部,且不在该双曲线渐近线上,
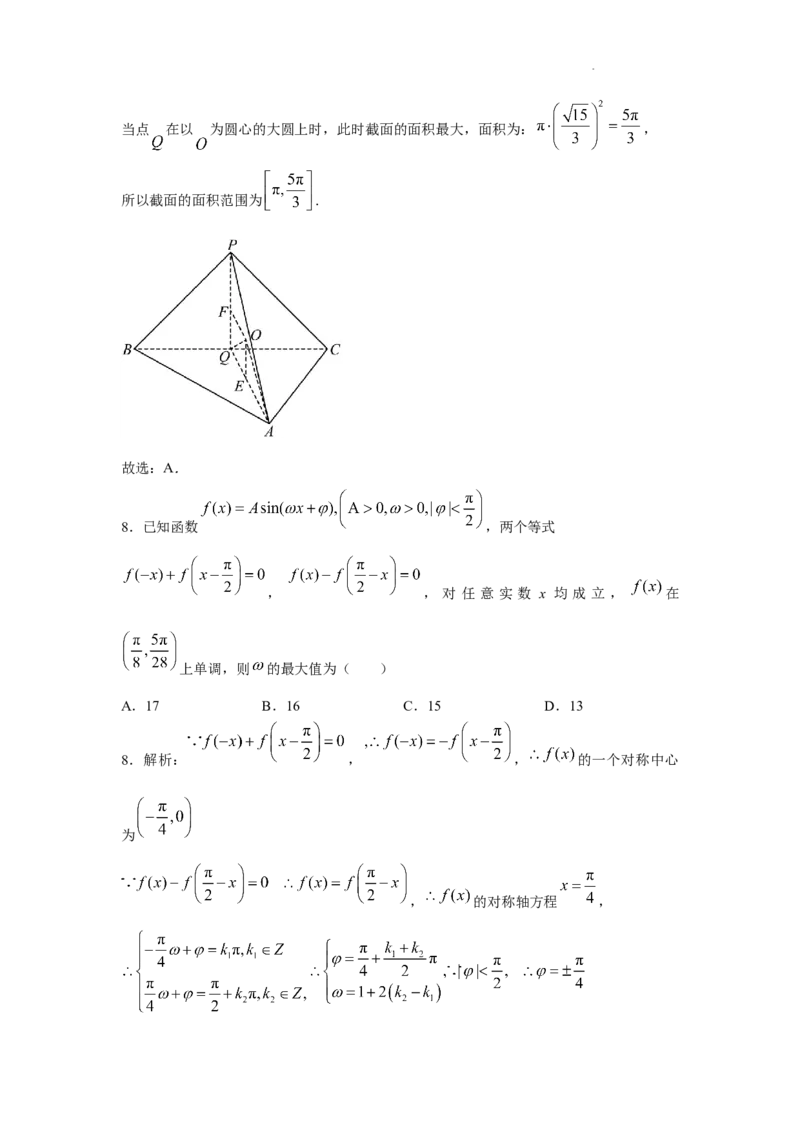
学科网(北京)股份有限公司临界情况时,点 在双曲线上,代入 ,可得 , ,
得 .
当渐近线经过点 时, 综上, ,
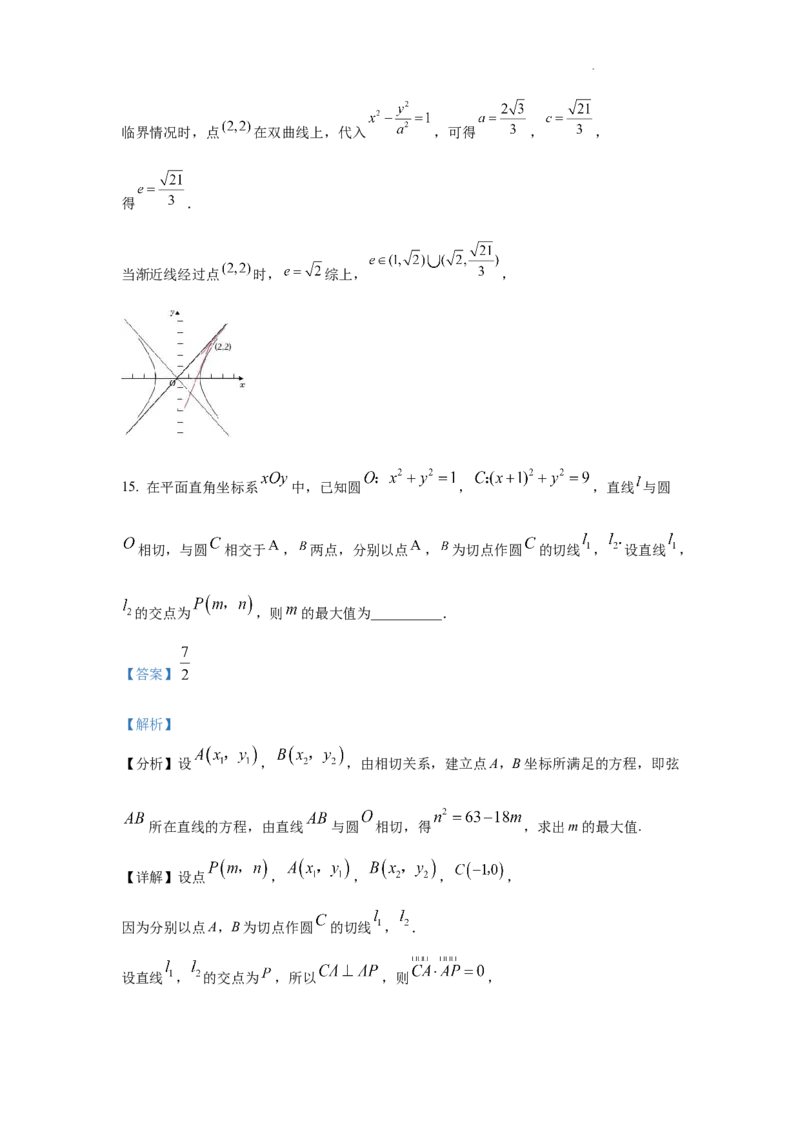
15. 在平面直角坐标系 中,已知圆 , ,直线 与圆
相切,与圆 相交于 , 两点,分别以点 , 为切点作圆 的切线 , 设直线 ,
的交点为 ,则 的最大值为__________.
【答案】
【解析】
【分析】设 , ,由相切关系,建立点A,B坐标所满足的方程,即弦
所在直线的方程,由直线 与圆 相切,得 ,求出m的最大值.
【详解】设点 , , , ,
因为分别以点A,B为切点作圆 的切线 , .
设直线 , 的交点为 ,所以 ,则 ,
学科网(北京)股份有限公司即 ,所以 ,因为
,
所以 ,即 是方程 的解,
所以点 在直线 上,
同理可得 在直线 上,
所以弦 所在直线的方程为 ,
因为直线 与圆 相切,所以 ,
解得 ,得 ,
即 的最大值为 .
故答案为:3.5
16. 已 知 长 方 体 的 底 面 是 边 长 为 的 正 方 形 , 若
,则该长方体的外接球的表面积为________;记 分别是
方向上的单位向量,且 , ,则 (m,
n为常数)的最小值为________.
【答案】 ①. ②.
【解析】
【分析】根据长方体外接球直径为长方体体对角线即可求出球半径,得出球的面积,由所
学科网(北京)股份有限公司给条件可取 与 的方向相同或与 的方向相同,问题可转化为求平面 上一
点 与 的距离的最小值,即求 到平面 的距离得解.
【详解】在 中, ,所以 ,
,
所以该长方体的外接球的半径为 ,所以该长方体的外接球的表面积为
由 及 可得
,
所以 与 的方向相同或与 的方向相同,
不妨取 与 的方向相同,
由平面向量基本定理可得 必与 共面,
在平面 上取一点 ,故可设 ,
则 ,所以其最小值为点 到平面 的最小值,即
最小值为 .
故答案为: ;
学科网(北京)股份有限公司四、解答题:本题共6小题,共70分.解答应写出相应的文宇说明、证明过程或演
算步骤.
17.(12分)
在锐角 中,角 所对的边分别是 ,满足 .
(1)求证: ;
(2)求 的取值范围.
17.解(1)由
由余弦定理 得
由正弦定理得:
又
都是锐角
(2)令
学科网(北京)股份有限公司由(1) 得
在锐角三角形 中
令
在 上单调递增
18.(12分)已知正项数列 ,其前n项和 ,满足 .
(1)求证:数列 是等差数列,并求出 的表达式;
(2)数列 中是否存在连续三项 ,使得 构成等差
数列?请说明理由.
(1) ;(2)不存在
a =√n−√n−1
n
19. 三棱台 的底面是正三角形, 平面 , , ,
,E是 的中点,平面 交平面 于直线l.
学科网(北京)股份有限公司(1)求证: ;
(2)求直线 与平面 所成角的正弦值.
【19题答案】
【答案】(1)证明略
(2)
20.(12分)2022年冬季奥林匹克运动会在北京胜利举行,北京也成为了第一个同时举办
过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市.为推
广普及冰雪运动,深入了解湖北某地中小学学生在“自由式滑雪”和“单板滑雪”两项活
动的参与情况,随机选取了10所学校进行研究,得到如下图数据:
(1)在这10所学校中随机选取3所来调查研究,求在抽到学校至少有一个参与“自由式
滑雪”超过40人的条件下,“单板滑雪”不超过30人的概率;
(2)现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这3个动作技巧进行集训,
且在集训中进行了多轮测试.规定:在一轮测试中,这3个动作中至少有2个动作达到
“优秀”.则该轮测试记为“优秀”,在集训测试中,小明同学滑行,转弯,停止三个动
作达到“优秀”的概率分别为 ,且各个动作互不影响且每轮测试互不影响.如果
小明同学在集训测试中要想获得“优秀”的次数的平均值达到3次,那么理论上至少要进
学科网(北京)股份有限公司行多少轮测试?
21. 已知函数 .
(1)若 ,求实数 的取值范围.
(2)求证: .
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)根据已知条件得 ,进而得出 ,利用不等式的性质及构造函数,
利用导数法求函数的最值即可求解;
(2)根据(1)的结论及已知条件,只需证当 时, 成立即可,转化
学科网(北京)股份有限公司成求函数的最值,利用不等式的性质构造函数及法求函数的最值即可求解.
【小问1详解】
因为 ,则 ,即 ,
反之当 时, ,
令 ,则 ,
设 ,由于 在 单调递增,且 ,
所以当 时, ,即 ,
当 时 ,即 ,
所以 在 上单调递减,在 上单调递增.
所以 ,即 ,所以 .
【小问2详解】
由(1)可知: ①
下面证明当 时, ②
等价于 ,设 ,
当 时,
当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 ,所以②式成立,
学科网(北京)股份有限公司由①、②可得: ,当 时取到“ ”,
取 有, ,
所以 ,不等式成立.
22.已知椭圆 的离心率为 ,且经过点 , 为椭
圆C的左右焦点, 为平面内一个动点,其中 ,记直线 与椭圆C在x
轴上方的交点为 ,直线 与椭圆C在x轴上方的交点为 .
(1)求椭圆C的标准方程;
(2)①若 ,证明: ;
②若 ,探究 之间关系.
22.解析:(1)由题意得: ,因此,椭圆 C 的标准方程为
(2)①(解法一)
, 即
学科网(北京)股份有限公司又 , 即
,即
① ( 解 法 二 )
,因此
① ( 解 法 三 ) 证 明 : 显 然 Q 在 椭 圆 内 , Q 为 与 的 交 点 ,
,
得 ,又 ,故只需证明:
成立.
②(解法一)设 (令 )
,消去 x 得: , ,
, , ,
学科网(北京)股份有限公司设 ,( 令 ), ,消去 x 得:
,
, ,
,
,
② ( 解 法 二 ) , 设 , 则
,
学科网(北京)股份有限公司于是
.
学科网(北京)股份有限公司学科网(北京)股份有限公司