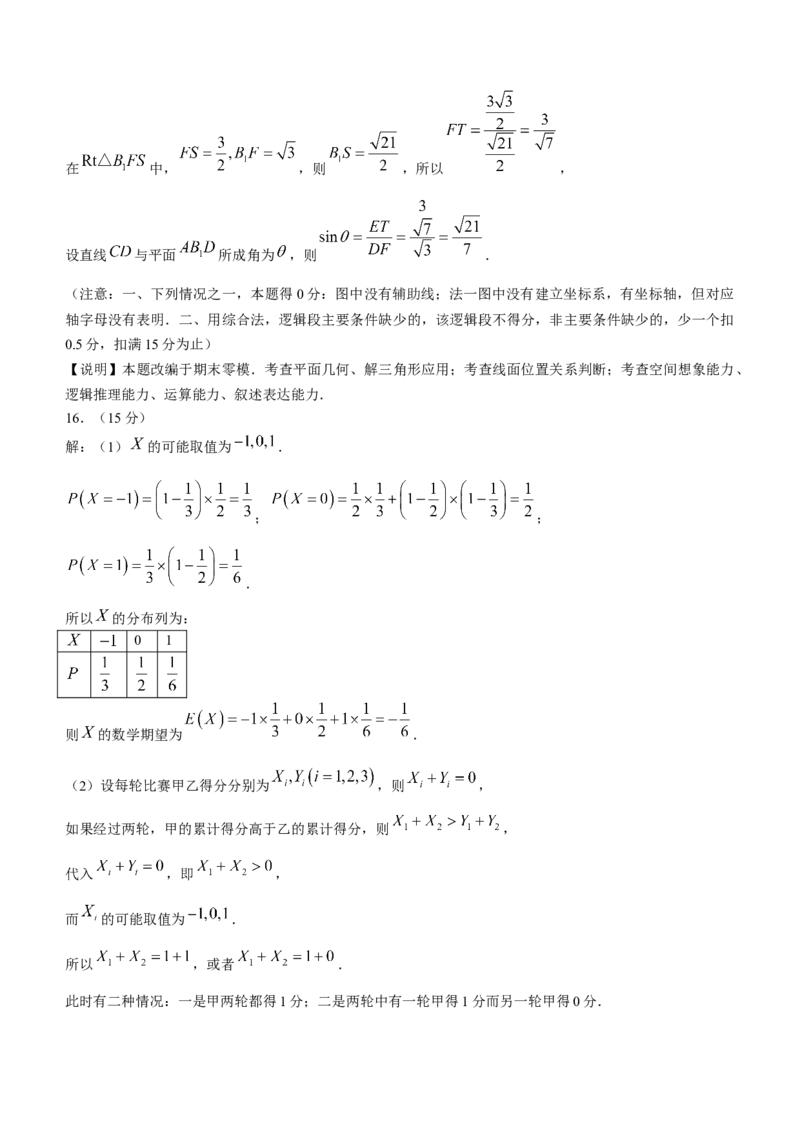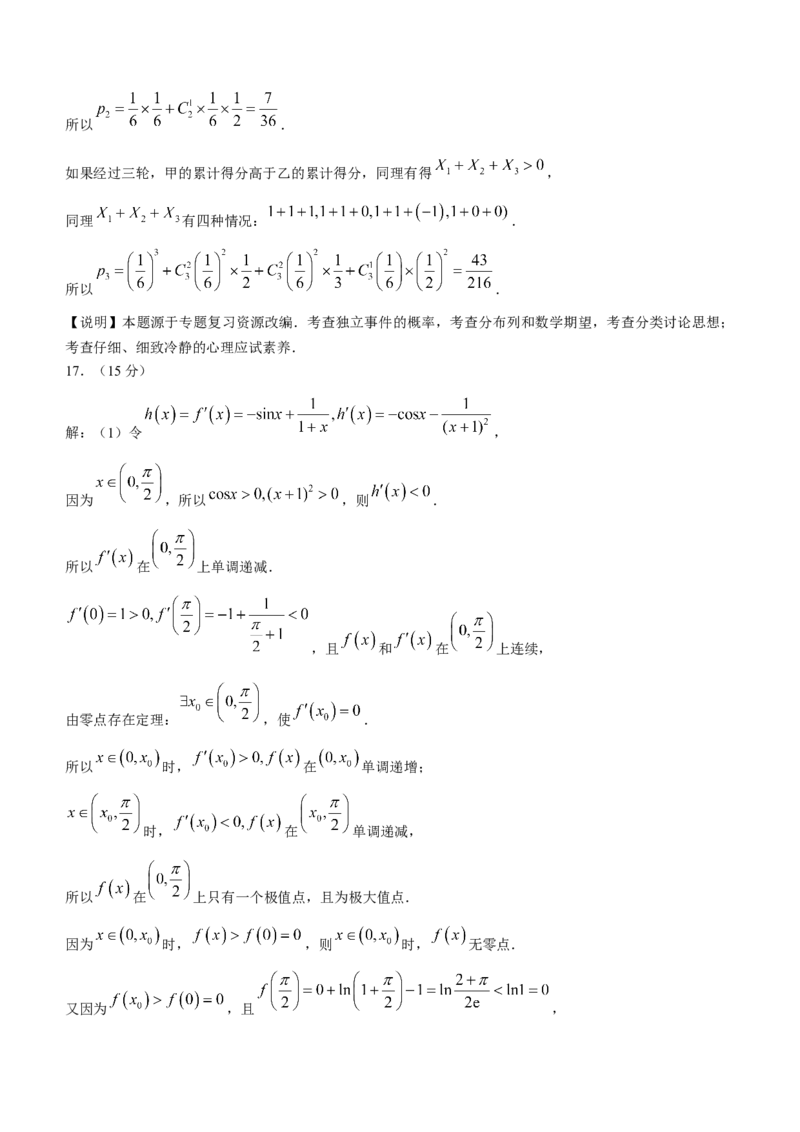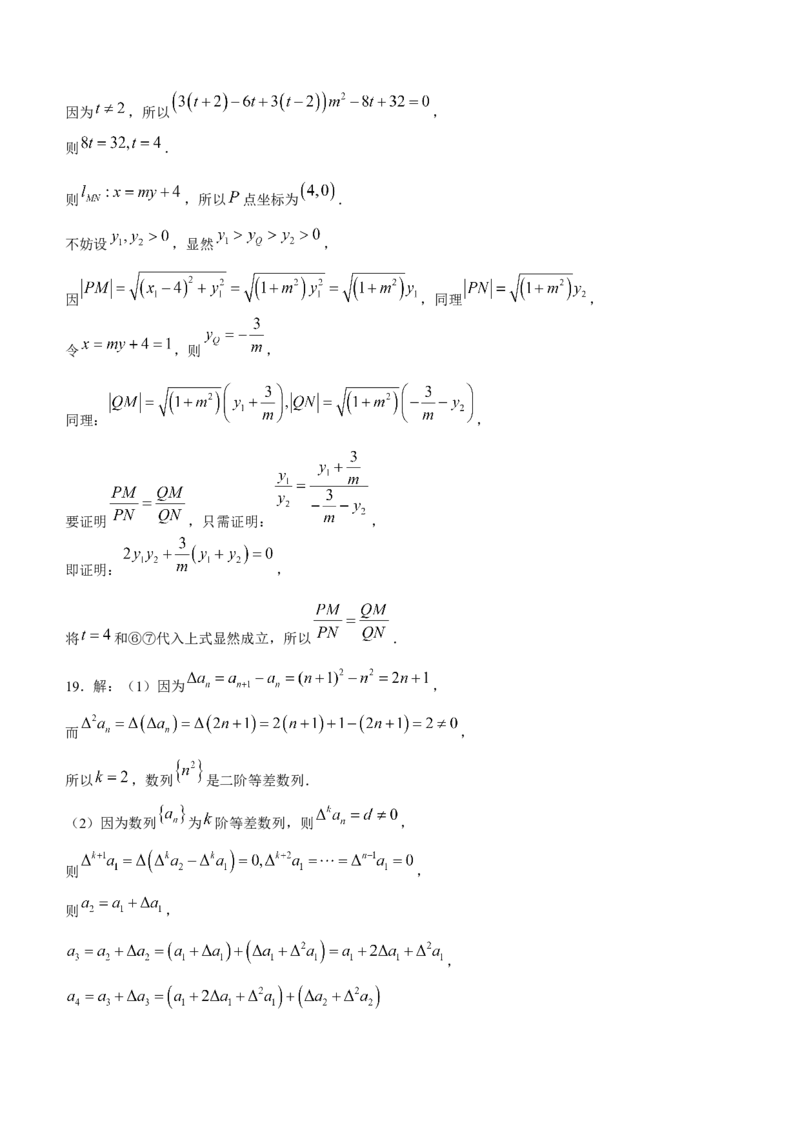文档内容
2023~2024 学年度第二学期高三期初试卷
数 学
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷
上无效。
3.本卷满分150分,考试时间120分钟。考试结束后,将答题卡交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的。
1.一组数据从小到大的顺序排列如下:9,10,12,15,17,18,22,26,经计算,则75%分位数是
( )
A.18 B.20 C.21 D.22
2.已知复数 满足 ,则 ( )
A.0 B.1 C. D.2
3.在 中, ,且 的面积为 ,则 ( )
A. B. C.2 D.3
4.已知正数 满足 ,则 的最小值为( )
A.6 B.7 C.8 D.9
5.已知平面内的向量 在向量 上的投影向量为 ,且 ,则 的值为( )
A. B.1 C. D.
6.等差数列 的首项为1,公差不为0.若 成等比数列,则 的前5项的和为( )
A. B. C.5 D.257.已知 ,则 的值为( )
A. B. C. D.2
8.已知过坐标原点 且异于坐标轴的直线交椭圆 于 两点, 为 中点,过
作 轴垂线,垂足为 ,直线 交椭圆于另一点 ,直线 的斜率分别为 ,若 ,
则粗圆离心率为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目
要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知 ,下列命题正确的是( )
A.命题“ ”的否定是“ ,使得 成立”
B.若命题“ 恒成立”为真命题,则
C.“ ”是“方程 有实数解”的充分不必要条件
D.若命题“ ”为真命题,则
10.正方体 的8个顶点中的4个不共面顶点可以确定一个四面体,所有这些四面体构成集
合 ,则( )
A. 中元素的个数为58
B. 中每个四面体的体积值构成集合 ,则 中的元素个数为2
C. 中每个四面体的外接球构成集合 ,则 中只有1个元素
D. 中不存在四个表面都是直角三角形的四面体
11.已知函数 ,则下列说法正确的是( )A. 是 的一个周期
B. 的最小值是
C.存在唯一实数 ,使得 是偶函数
D. 在 上有3个极大值点
三、填空题:本题共3小题,每小题5分,共15分。
12.与圆 和圆 都相切的直线方程是______.
13.已知 是圆锥 的底面直径, 是底面圆周上的一点, ,则二面角
的余弦值为______.
14.如果函数 在区间 上为增函数,则记为 ,函数 在区间 上为减函数,则记
为 .已知 ,则实数 的最小值为______;函数 ,且
,则实数 ______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
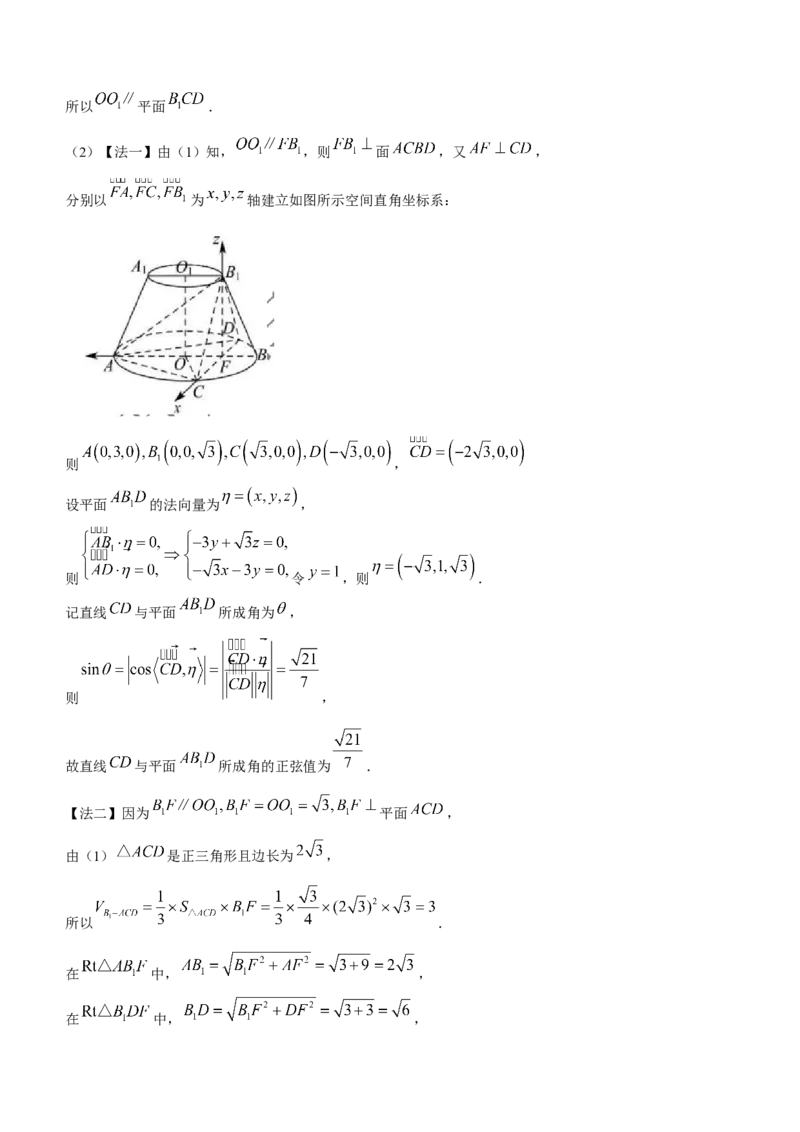
15.(13分)
在如图所示的圆台中, 是下底面圆 的直径, 是上底面圆 的直径, ,
为圆 的内接正三角形.
(1)证明: 平面 ;
(2)求直线 与平面 所成角的正弦值.16.(15分)
为了释放学生压力,某校进行了一个投篮游戏.甲、乙两人轮流进行篮球定点投篮比赛每人各投一次为一轮.
每人投一次篮,两人中只有1人命中,命中者得1分,未命中者得 分;两人都命中或都未命中,两人均得
0分.设甲每次投篮命中的概率为 ,乙每次投篮命中的概率为 ,且各次投篮结果互不影响.
(1)经过1轮投篮,记甲的得分为 ,求 的分布列及数学期望;
(2)用 表示经过第 轮投篮后,甲的累计得分高于乙的累计得分的概率,求 .
17.(15分)
已知函数 .
(1)判断函数 在区间 上极值点和零点的个数,并给出证明;
(2)若 恒成立,求实数 .
18.(17分)
已知双曲线 的两条渐近线分别为 上一点 到 的距离之积为
.
(1)求双曲线 的方程;
(2)设双曲线 的左、右两个顶点分别为 为直线 上的动点,且 不在 轴上,直线 与
的另一个交点为 ,直线 与 的另一个交点为 ,直线 与 轴的交点为 ,直线 与 的交
点为 ,证明 .
19.(17分)
对 于 数 列 , 记 , 称 数 列 为 数 列 的 一 阶 差 分 数 列 ; 记
,称数列 为数列 的二阶差分数列,…,一般地,对于 ,记
,规定: ,称 为数列 的 阶差分数列.对于数列 ,如果 ( 为常数),则称数列 为 阶等差数列.
(1)数列 是否为 阶等差数列,如果是,求 值,如果不是,请说明为什么?
(2)请用 表示 ,并归纳出表示 的正确结论(不要求证明);
(3)请你用(2)归纳的正确结论,证明:如果数列 为 阶等差数列,则其前 项和为
;
(4)某同学用大小一样的球堆积了一个“正三棱锥”,巧合用了2024个球.第1层有1个球,第2层有3个,
第3层有6个球,…,每层都摆放成“正三角形”,从第2层起,每层“正三角形”的“边”都比上一层的
“边”多1个球,问:这位同学共堆积了多少层?高三数学期初考试评分标准
一、选择题
题 答案 出处 考查知识 能力素养
号
1 B 课本题改编 百分位数 运算求解
2 C 课本题改编 复数模的运算及性质 运算求解
3 B 课本题改编 余弦定理,面积公式 运算求解
4 D 复习题改编 排列组合 分类讨论思想,数学抽象
5 A 复习题改编 投影向量,向量的模 运算求解
6 A 复习题改编 等差、等比数列基本量运算 运算求解
7 A 复习题改编 两角和与差的正余弦公式 转化思想,运算求解
8 D 原创 椭圆第三定义,离心率 转化思想,运算求解
二、选择题(有错误答案,该题得0分,如果有两个答案,该题分值为3分和6分;如果有三
个答案,该题分值为2分、4分、6分)
题号 答案 出处 考查知识 能力素养
9 BCD 高一试卷 逻辑,恒成立有解问题 逻辑推理
10 ABC 期末零模 立体几何 空间想象,分类讨论
11 ACD 原创 三角函数图象与性质 数形结合,分类讨论
三、填空题
题
答案 出处 考查知识 能力素养
号
12 复习题 公切线,两圆位置关系 转化思想,数形结合
13 期末零模 二面角 空间想象,数学转化
14 第一空2,第二空3 原创 新定义的理解,函数单调性 数学转化
四、解答题
15.(13分)
证明:(1)记 与 交于点 ,连接 ,
因为 是下底面圆 的直径,且 为圆 的内接正三角形,
所以 垂直平分 ,则 ,
中, .
因为 ,则 ,
所以 ,所以四边形 为平行四边形,所以 ,
又 平面 平面 ,所以 平面 .
(2)【法一】由(1)知, ,则 面 ,又 ,
分别以 为 轴建立如图所示空间直角坐标系:
则 ,
设平面 的法向量为 ,
则 令 ,则 .
记直线 与平面 所成角为 ,
则 ,
故直线 与平面 所成角的正弦值为 .
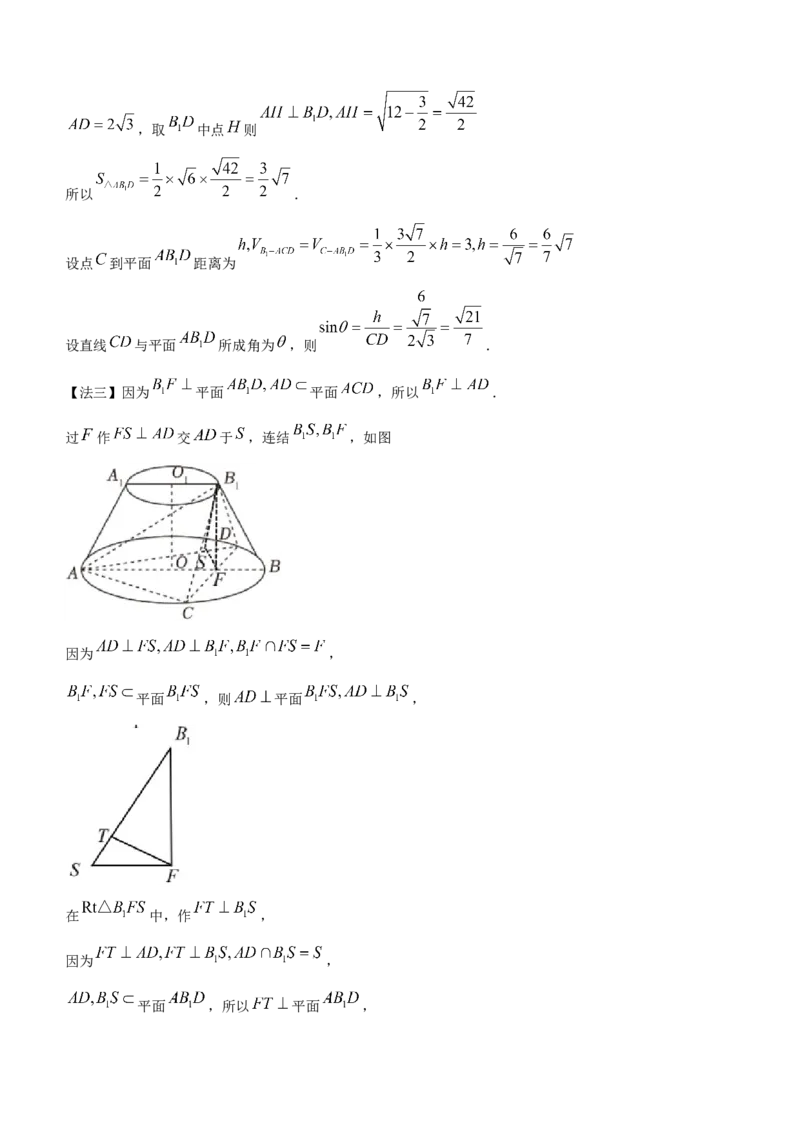
【法二】因为 平面 ,
由(1) 是正三角形且边长为 ,
所以 .
在 中, ,
在 中, ,,取 中点 则
所以 .
设点 到平面 距离为
设直线 与平面 所成角为 ,则 .
【法三】因为 平面 平面 ,所以 .
过 作 交 于 ,连结 ,如图
因为 ,
平面 ,则 平面 ,
在 中,作 ,
因为 ,
平面 ,所以 平面 ,在 中, ,则 ,所以 ,
设直线 与平面 所成角为 ,则 .
(注意:一、下列情况之一,本题得0分:图中没有辅助线;法一图中没有建立坐标系,有坐标轴,但对应
轴字母没有表明.二、用综合法,逻辑段主要条件缺少的,该逻辑段不得分,非主要条件缺少的,少一个扣
0.5分,扣满15分为止)
【说明】本题改编于期末零模.考查平面几何、解三角形应用;考查线面位置关系判断;考查空间想象能力、
逻辑推理能力、运算能力、叙述表达能力.
16.(15分)
解:(1) 的可能取值为 .
; ;
.
所以 的分布列为:
0 1
则 的数学期望为 .
(2)设每轮比赛甲乙得分分别为 ,则 ,
如果经过两轮,甲的累计得分高于乙的累计得分,则 ,
代入 ,即 ,
而 的可能取值为 .
所以 ,或者 .
此时有二种情况:一是甲两轮都得1分;二是两轮中有一轮甲得1分而另一轮甲得0分.所以 .
如果经过三轮,甲的累计得分高于乙的累计得分,同理有得 ,
同理 有四种情况: .
所以 .
【说明】本题源于专题复习资源改编.考查独立事件的概率,考查分布列和数学期望,考查分类讨论思想;
考查仔细、细致冷静的心理应试素养.
17.(15分)
解:(1)令 ,
因为 ,所以 ,则 .
所以 在 上单调递减.
,且 和 在 上连续,
由零点存在定理: ,使 .
所以 时, 在 单调递增;
时, 在 单调递减,
所以 在 上只有一个极值点,且为极大值点.
因为 时, ,则 时, 无零点.
又因为 ,且 ,因为 在 单调递减,则存在唯一零点 ,使 .
所以 在 上只有一个零点,只有有一个极大值点.
(2)令 ,
由 恒成立,得 .
因为 图象在定义域上连续不间断,
只需 是 的一个极大值点.
因为 ,则 ,解得 .
下证:当 时, 恒成立.
因为 .
(1)当 时, 在 上单调递增,
所以 .
(2)当 时,
令 ,
则 在 单调递减,
则 .又因为
所以当 时,
综上,当 时, 恒成立.
【说明】本题改编.考查函数的单调性、最值、极值、零点;考查导数的应用;考查恒成立题型解决方法;
考查运算能力、叙述表达能力、分析思维能力、转化能力;考查思维的方法途径策略;考查应试方法.18.(17分)
(1)因为 在 上,则 ①.
因为 的方程分别为 .
到 的距离之积为 ,则 ,
化简得: ②,
由①②解得 ,
所以双曲线 的方程为 ③.
(2)因为 ,设
则 ,
所以 ④,
因为 ,
且 在双曲线上,则 ,代入上式得: ,
把④代入上式得: ⑤.
设直线 ,代入①得:
,则: ⑥, ⑦,
由⑤得: ,即: ,
把⑥⑦代入上式得: ,因为 ,所以 ,
则 .
则 ,所以 点坐标为 .
不妨设 ,显然 ,
因 ,同理 ,
令 ,则 ,
同理: ,
要证明 ,只需证明: ,
即证明: ,
将 和⑥⑦代入上式显然成立,所以 .
19.解:(1)因为 ,
而 ,
所以 ,数列 是二阶等差数列.
(2)因为数列 为 阶等差数列,则 ,
则 ,
则 ,
,.
归纳得一般结论: ①.
(3)设数列: ,因为 ,
所以数列 为 阶等差数列,
由(2)中①得: ,因为
所以 .
(4)由(1)知数列 为二阶等差数列,
且 ,
则由(3)得:
②.
(注意:如果没有证明上面结论,此处扣2分.证明方法不限)
设共堆积了 层,第 层共有 个球,第1层有1个球,因为每层的“边”比上一层多1个球,所以第 层
的“边”共有 个球,则第 层的球数为 .
则这 层所有球的个数为 .
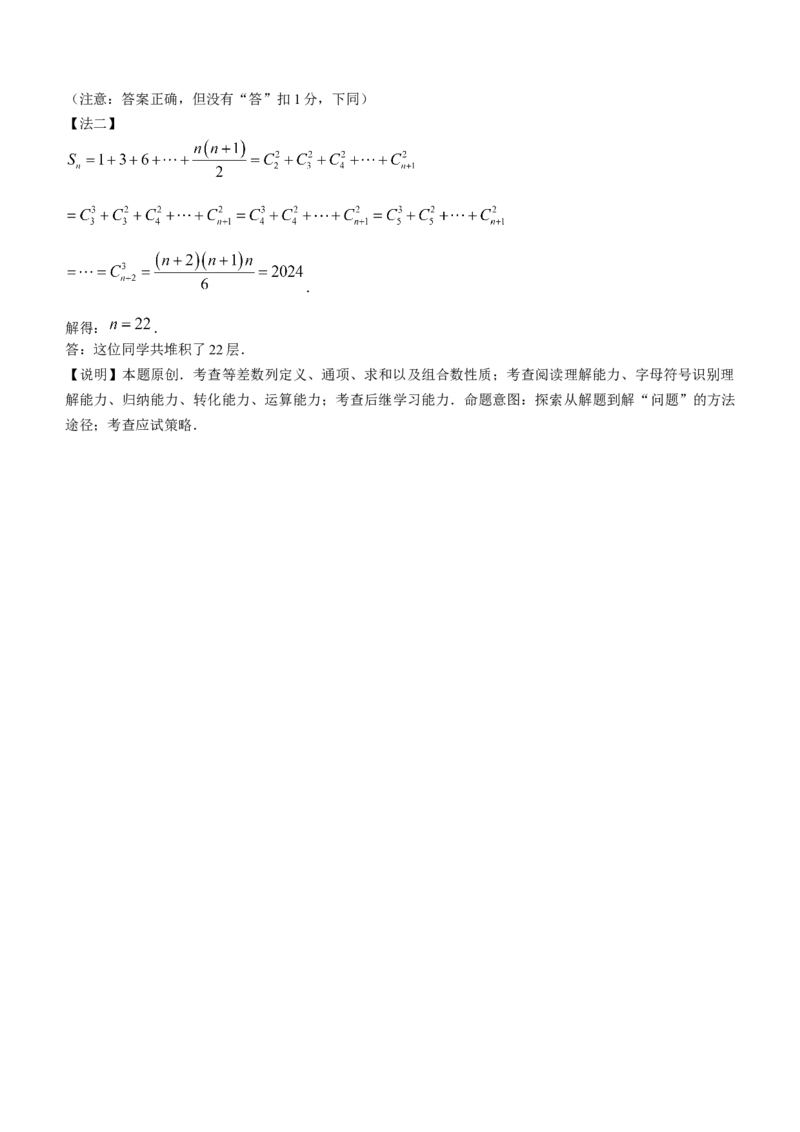
【法一】由②式得:
.
解得: .
答:这位同学共堆积了22层.(注意:答案正确,但没有“答”扣1分,下同)
【法二】
.
解得: .
答:这位同学共堆积了22层.
【说明】本题原创.考查等差数列定义、通项、求和以及组合数性质;考查阅读理解能力、字母符号识别理
解能力、归纳能力、转化能力、运算能力;考查后继学习能力.命题意图:探索从解题到解“问题”的方法
途径;考查应试策略.