文档内容
2024 届高三年级第二学期期初测试
数 学
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共4页,总分150分,考试时间120
分钟。
第I卷(选择题共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1. 已知集合A={x∈R|x2-2x-3<0},集合B={x∈R|log (x+2)<1},则A∩B=
2
A.(-3,2) B.(-2,3) C.(-2,0) D.(-1,0)
2. 已知复数z满足(1-i)z=3-i,则复数| |=
A.2 B. C.2 D.
3. 在∆ABC中,“A=B”是“cos A+sin A=cos B+sin B”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
4. 我国周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例,在西方,最早提出
并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他们用演绎法证明了直角
三角形斜边的平方等于两直角边的平方之和.在 3,4,5,6,8,10,12,13这8个数中任取
3个数,这3个数恰好可以组成勾股定理关系的概率为
A. B. C. D.
5. 已知圆台的上底面半径为1,下底面半径为2,母线与下底面所成的角为 ,则该圆
台的体积为
A. B. C. D.
6. 若(2-x)10的展开式中二项式系数和为A,所有项系数和为B,一次项系数为C,则A
+B+C=
A.4095 B.4097 C.-4095 D.-4097
7. 已知正实数x,y满足x+y=1,则 的最大值为
学科网(北京)股份有限公司A. B. C. D.
8. 若x,x 是关于x的方程3sin2x-cos2x=a在[0, ]内的两根,则tan(x+x)的值为
1 2 1 2
A.-3 B.3 D.- D.
二、多选题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合
题目要求。全部选对的得6分,部分选对的得3分,有选错的得0分。
9. 已知向量a=(1,-2),b=(1,3),则下列结论正确的是
A.b在a上的投影向量是(1,-2) B.|2a+b|=|b|
C.a与b的夹角为 D.(a+b)⊥a
10.以下四个命题表述正确的是
A.直线(3+m)x+4y-3+3m=0(x∈R)恒过定点(-2,3)
B.圆x2+y2=4上有且仅有3个点到直线l:x-y+ =0的距离都等于1
C.曲线C :x2+y2+2x=0与曲线C :x2+y2-4x-8y+m=0恰有三条公切线,则m=
1 2
4
D.若双曲线 =1(a>0,b>0)的一条渐近线被圆x2+y2-6x=0截得的弦长为2
,则双曲线的离心率为
11.设定义在(0,+∞)上的函数f(x)的导函数为f'(x),若满足xf(x)+x2f(x)=1,且
f(1)=0,则下列说法正确的是
A.f(2)>f(3) B.若f(x)=f(x),且x≠x,则x+x=2e
1 2 1 2 1 2
C.f(x)的最大值为 D.若xf((x)≥eλ,则λ≤0
第II卷(非选择题共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12.已知等比数列{a}的公比为2,前n项和为S ,且7,a ,a 成等差数列,则S = ▲
n n 2 6 6
.
13.为了调查某苹果园中苹果的生长情况,在苹果园中随机采摘了 100个苹果.经整理分
析后发现,苹果的重量x(单位:kg)近似服从正态分布N(0.4,σ2),已知P(x<0.1)=
学科网(北京)股份有限公司0.1,P(x>0.5)=0.3.若从该苹果园中随机采摘 1 个苹果,则该苹果的重量在
(0.5,0.7]内的概率为 ▲ .
14.在正三棱锥A-BCD中,底面∆BCD的边长为4,E为AD的中点,AB⊥CE,则以AD
为直径的球截该棱锥各面所得交线长为 ▲ .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
在∆ABC中,角A,B,C所对的边分别为a,b,c,cos A= .
(1)求 的值;
(2)若a=2 ,∆ABC的面积为 ,求b的值.
16.(15分)
篮球是一项风靡世界的运动,是深受大众喜欢的一项运动.
喜爱篮球运动 不喜爱篮球运动 合计
男性 60 40 100
女性 20 80 100
80
合计 120 200
(1)为了解喜爱篮球运动是否与性别有关,随机抽取了男性和女性各 100名观众进行调
查,得到如上2×2列联表,判断是否有99.9% 把握认为喜爱篮球运动与性别有关;
(2)校篮球队中的甲、乙、丙三名球员将进行传球训练,第 1次由甲将球传出,每次传
球时,传球者都等可能的将球传给另外两个人中的任何一人,如此不停地传下去,且假定
每次传球都能被接到,记开始传球的人为第 1次触球者,第n次触球者是甲的概率记为
P,即P=1.
n 1
①求P(直接写出结果即可);
3
②证明:数列{P- }为等比数列,并比较第9次与第10次触球者是甲的概率的大小.
n
P 0.100 0.050 0.025 0.010 0.001
x 2.706 3.841 5.024 6.635 10.828
0
附:χ2= ,n=a+b+c+d.
学科网(北京)股份有限公司17.(15分)
已知函数f(x)=xex-kx2,k∈R.
(1)当k=0时,求函数f(x)在[-2,2]上的值域;
(2)若函数f(x)在(0,+∞)上仅有两个零点,求实数k的取值范围.
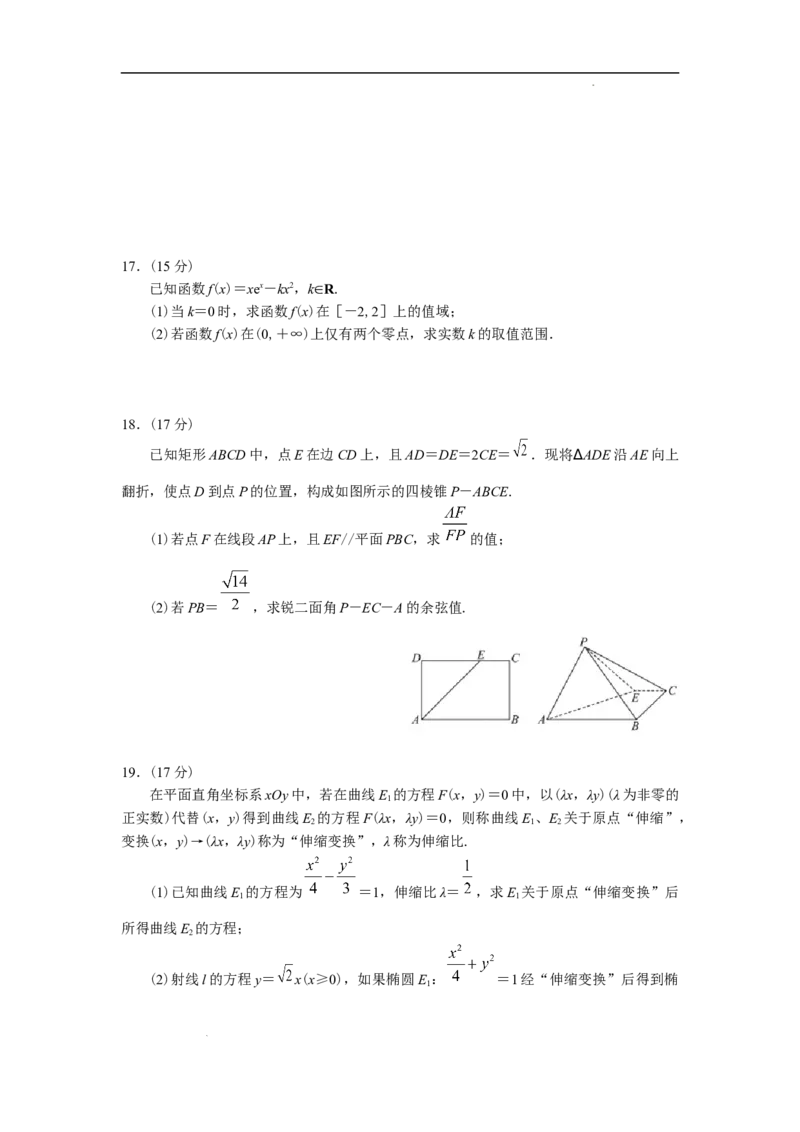
18.(17分)
已知矩形ABCD中,点E在边CD上,且AD=DE=2CE= .现将∆ADE沿AE向上
翻折,使点D到点P的位置,构成如图所示的四棱锥P-ABCE.
(1)若点F在线段AP上,且EF//平面PBC,求 的值;
(2)若PB= ,求锐二面角P-EC-A的余弦值.
19.(17分)
在平面直角坐标系xOy中,若在曲线E 的方程F(x,y)=0中,以(λx,λy)(λ为非零的
1
正实数)代替(x,y)得到曲线E 的方程F(λx,λy)=0,则称曲线E 、E 关于原点“伸缩”,
2 1 2
变换(x,y)→(λx,λy)称为“伸缩变换”,λ称为伸缩比.
(1)已知曲线E 的方程为 =1,伸缩比λ= ,求E 关于原点“伸缩变换”后
1 1
所得曲线E 的方程;
2
(2)射线l的方程y= x(x≥0),如果椭圆E : =1经“伸缩变换”后得到椭
1
学科网(北京)股份有限公司圆E,若射线l与椭圆E、E 分别交于两点A、B,且|AB|= ,求椭圆E 的方程;
2 1 2 2
(3)对抛物线E :x2=2py,作变换(x,y)→(λx,λy),得抛物线E :x2=2py;对E
1 1 1 1 2 2 2
作变换(x,y)→(λx,λy),得抛物线E :x3=2py;如此进行下去,对抛物线E :x2=2py
2 2 3 3 n n
作变换(x,y)→(λx,λy), 得抛物线E :x2=2p y,….若p =1,λ =2n,求数列
n n n+1 n+1 1 n
{p}的通项公式p.
n n
学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司