河北省衡水市2024届高三下学期大数据应用调研联合测评（+VIII）数学试题(无答案)_2024年5月_01按日期_23号_2024届河北省高三大数据应用调研联合测评（Ⅷ）

绝密★启用前 河北省 2024 届高三年级大数据应用调研联合测评（Ⅷ） 数学 班级__________姓名__________ 注意事项： 1.答卷前，考生务必将自己的姓名､班级和考号填写在答题卡上. 2.回答选择题时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需 改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在 本试卷上无效. 3.考试结束后，将本试卷和答题卡一并交回. 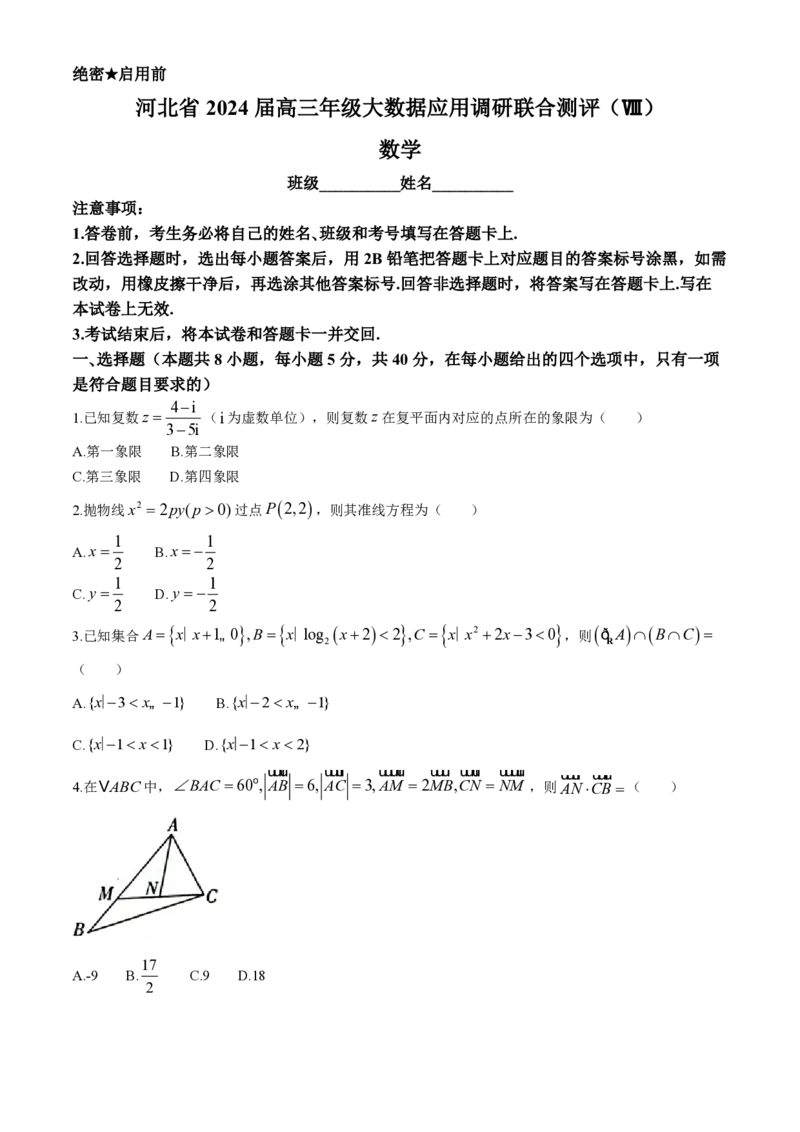一､选择题（本题共 8小题，每小题 5分，共 40分，在每小题给出的四个选项中，只有一项 是符合题目要求的） 4i 1.已知复数z  （i为虚数单位），则复数z在复平面内对应的点所在的象限为（ ） 35i A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.抛物线x2 2py(p 0)过点P2,2 ，则其准线方程为（ ） 1 1 A.x B.x 2 2 1 1 C.y  D.y  2 2 3.已知集合Ax∣x1„ 0,B  x∣log x22  ,C   x∣x2 2x30  ，则 ð ABC 2 R （ ） A.{x∣3 x„ 1} B.{x∣2 x„ 1} C.{x∣1 x1} D.{x∣1 x2} uuur uuur uuuur uuur uuur uuuur uuur uuur 4.在VABC中，BAC 60o, AB 6, AC 3,AM 2MB,CN  NM ，则ANCB（ ） 17 A.-9 B. C.9 D.18 2 学科网（北京）股份有限公司a2 3    5.设a 0,a 1，若函数 f x alog x2 1x 是偶函数，则a （ ）  ax 1  a 1 3 A. B. C.2 D.3 2 2 6.在正三棱锥PABC 中，AB2,M,N分别是PB,BC的中点，AM  PN，则三棱锥PABC 的体 积为（ ） 6 5 3 2 A. B. C. D. 3 3 3 3 x2 y2 1 7.已知椭圆C:  1(a b0)的左､右焦点分别为F,F ，过F 向圆x2  y2  b2引切线交椭圆 a2 b2 1 2 2 4 于点P,O为坐标原点，若 OP  OF ，则椭圆的离心率为（ ） 2 1 3 5 2 A. B. C. D. 2 2 3 3 8.已知函数 f xlnx1ax有两个零点x ,x ，且x  x ，则下列命题正确的是（ ） 1 2 1 2 2 A.a 1 B.x x  1 2 a 1 C.x x 1 D.x x  1 1 2 2 1 a 二､多选题（本题共 3小题，每小题 6分，共 18分.在每小题给出的四个选项中，有多项符合 题目要求，全部选对的得 6分，部分选对的得部分分，有选错的得 0分） 4 π π 9.已知函数 f xsin  x 的图象向左平移 个单位后得到gx 的图象，则下列结论正确的是 3 6 4 （ ） 4 2π A.gxcos  x  3 3  π B.gx 的图象关于x 对称 4  π  C.gx 的图象关于  ,0 对称  8   π π D.gx 在  , 上单调递增  2 4    2  10.已知A 0, 2 ,B0, ，动点Px,y 满足 PA  2 PB ，则下列结论正确的是（ ）   2   学科网（北京）股份有限公司A.点P的轨迹围成的图形面积为π 2 B. PB 的最小值为1 2 π C.P,P 是P的任意两个位置点，则PAP„ 1 2 1 2 3 1 1 D.过点 , 的直线与点P的轨迹交于点M,N ，则MN 的最小值为 2 2 2 11.已知数列 a  是公差为dd 0 的等差数列，若它的前2m(m1)项的和S 0，则下列结论正确 n 2m 的是（ ） A.若d 0，使a 0的最大n的值为m n B.S 是S 的最小值 m n C.3a2 a2 a2 3a2 m m2 m1 m1 D.a2 a2 a2 a2 m1 m m1 m2 三､填空题（本题共 3小题，每小题 5分，共 15分.第 14题第一空 2分，第二空 3分） 12.已知tan 2 ，则cos2__________. 13.已知正项等比数列 a  的前n项和为S ，若mN*且22mS S   22m 1  S ，则数列 a  的公 n n 3m m 2m n 比为__________. 14.一个1，两个2，三个3组成一个六位数，则相同数字不相邻的个数为__________.相同数字不相邻的概 率为__________. 四､解答题（本题共 5小题，共 77分.解答应写出必要的文字说明､证明过程或演算步骤） 15.（本小题满分13分）某公司招聘大学生的笔试测试题有一道6分的不定项选择题，共有A､B､C三个选 项，该不定项选择题正确答案最少一个选项，最多三个选项，全部选对得6分，部分选对得部分分，即若 有三个选项正确，某同学选择了两个正确选项，可得4分，选择一个正确选项可得2分，有选错的得0 分，若有两个正确选项，选择一个正确选项可得3分，有选错的得0分.某同学三个选项均不会做，只能靠 1 运气猜，每个选项选与不选的概率均占 .已知该同学对该题选择了若干个答案，不会不选. 2 （1）求该同学对该题选择两个答案的概率； （2）若该题正确答案是BC，求该同学得分X 的分布列和数学期望. 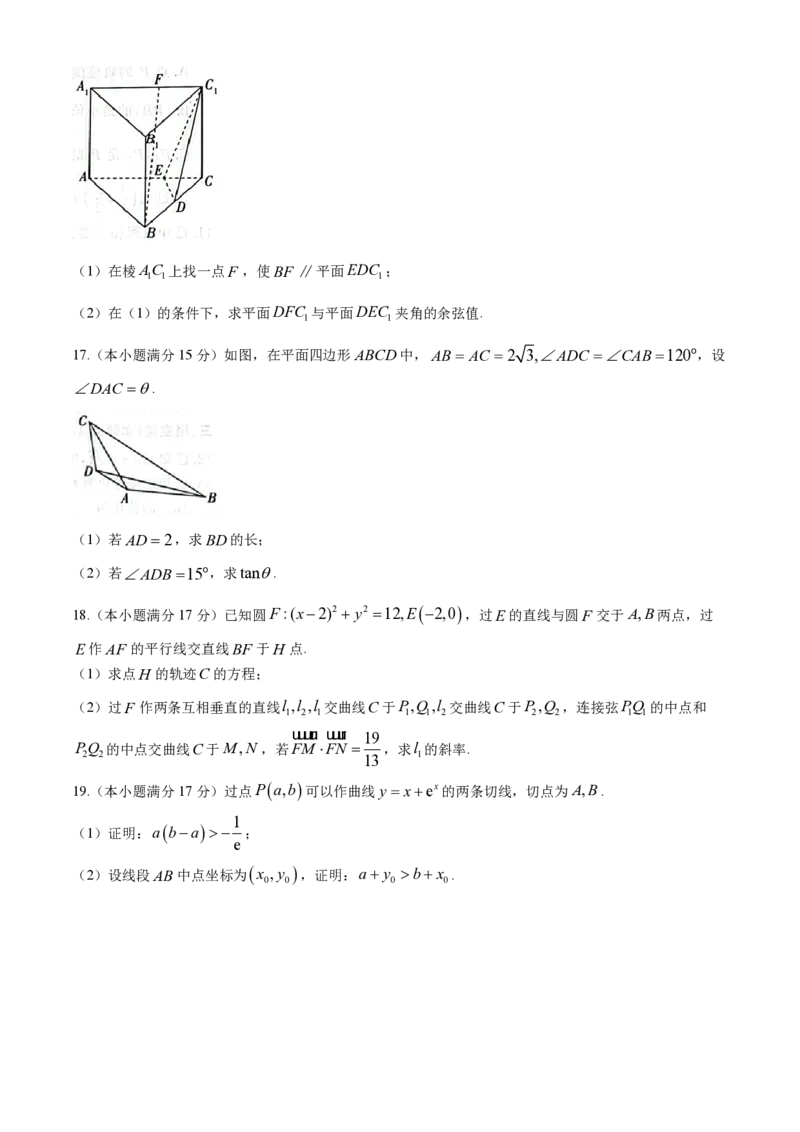16.（本小题满分15分）在棱长均相等的正三棱柱ABCABC 中，D是BC的中点，E是AC的三等 1 1 1 分点，且AE 2EC . 学科网（北京）股份有限公司（1）在棱AC 上找一点F ，使BF ∥平面EDC ； 1 1 1 （2）在（1）的条件下，求平面DFC 与平面DEC 夹角的余弦值. 1 1 17.（本小题满分15分）如图，在平面四边形ABCD中，AB AC 2 3,ADC CAB120o，设 DAC . （1）若AD2，求BD的长； （2）若ADB15o，求tan. 18.（本小题满分17分）已知圆F:(x2)2  y2 12,E2,0 ，过E的直线与圆F 交于A,B两点，过 E作AF 的平行线交直线BF 于H 点. （1）求点H 的轨迹C的方程； （2）过F 作两条互相垂直的直线l ,l ,l 交曲线C于P,Q,l 交曲线C于P,Q ，连接弦PQ 的中点和 1 2 1 1 1 2 2 2 1 1 uuuur uuur 19 PQ 的中点交曲线C于M,N ，若FM FN  ，求l 的斜率. 2 2 13 1 19.（本小题满分17分）过点Pa,b 可以作曲线y  xex的两条切线，切点为A,B. 1 （1）证明：aba ； e （2）设线段AB中点坐标为 x ,y  ，证明：a y bx . 0 0 0 0 学科网（北京）股份有限公司