文档内容
南昌二中 2024 届高三“九省联考”考后适应性测试数学试题一
本套试卷根据九省联考题型命制,题型为 8+3+3+5模式
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 数据6.0,7.4,8.0,8.4,8.6,8.7,9.0,9.1的50百分位数为( )
A. 8.4 B. 8.5 C. 8.6 D. 8.7
【答案】B
【解析】
【分析】根据给定条件,利用第50百分位数的定义计算即得.
【详解】依题意,一组数据的第50百分位数即为该组数据的中位数,
8.4+8.6
所以数据6.0,7.4,8.0,8.4,8.6,8.7,9.0,9.1的第50百分位数为 =8.5.
2
故选:B
x2
2. 已知双曲线C: y2 − =1(b>0)的离心率e< 2,则b的取值范围是( )
b2
A. (0,1) B. (1, 2) C. (1,+∞) D. ( 2,+∞)
【答案】A
【解析】
【分析】根据双曲线方程,求出离心率,由已知离心率范围列出不等式可解得的范围.
【详解】由已知可得双曲线的焦点在y轴上时,a =1,c2 =1+b2,
c 1+b2
所以e= = < 2,
a 1
1+b2 <2,由b>0,解得0cos2x>sinx⋅cos2x,
6 4 2 2 2
即g(x)> f(x)> f(x)⋅g ( x ) ,(一个正数乘以一个小于1的正数,积一定小于这个数)故排除A,D.
( )
对于B,设F(x)=4cos2xsinx=4sinx−8sin3 x,则 f′(x)= 4cosx 1−6sin2 x .
π π 1 2
因为当x∈ , 时, 0,即cos2x+
2
2sinx>4cos2xsinx,故B错误.
π 1 π 2
对于C,令G(x)=sinx+sinx⋅cos2x−2cos2x,因为G =− <0,G = >0,且函数
6 4 4 2
第4页/共23页
学科网(北京)股份有限公司G(x)的图象是连续不断的,
π π π π
所以函数G(x)在 , 内存在零点θ,即存在θ∈ , ,使得sinθ+sinθ⋅cos2θ−2cos2θ=0,
6 4 6 4
π π
即存在θ∈ , ,使得2cos2θ=sinθ+sinθ⋅cos2θ,故C正确.
6 4
故选:C.
【点睛】方法点睛:复合函数求导的一般步骤:(1)分析清楚函数y =h(x)是由哪些函数复合成的,也就
是找出y = f(u),u = g(x),使得h(x)= f(g(x));(2)分别求y对u的导数 f′(u)和u对x的导数
g′(x),再根据复合函数的求导法则,得到h′(x)= f′(u)g′(x),注意最后结果中要把 f′(u)写成 f′(g(x))
的形式.
PA
8. 已知平面上两定点A、B,则所有满足 =λ(λ>0且λ≠1)的点P的轨迹是一个圆心在AB上,
PB
λ
半径为 ⋅ AB 的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称作阿氏圆.已知棱长为3的正
1−λ2
方体ABCD−ABC D 表面上动点P满足 PA =2 PB ,则点P的轨迹长度为( )
1 1 1 1
4π 4π 3π ( )
A. 2π B. + 3π C. + D. 2+ 3 π
3 3 2
【答案】C
【解析】
【分析】根据阿氏圆性质求出阿氏圆圆心O位置及半径,P在空间内轨迹为以O为球心的球,球与面ABCD,
ABB A ,BCC B 交线为圆弧,求出截面圆的半径及圆心角,求出在截面内的圆弧的长度即可.
1 1 1 1
【详解】
( )
在平面中,图①中以B为原点以AB为x轴建系如图,设阿氏圆圆心O a,0 ,半径为r,
|PA| 2 2
|PA|=2|PB|,∴ =2,∴r = ⋅| AB|= ×3=2,
|PB| 1−22 3
AM
设圆O与AB交于M,由阿氏圆性质知 =λ=2,
MB
第5页/共23页
学科网(北京)股份有限公司|BM |=2−|BO|=2−a, ∴| AM |=2|BM |=4−2a,
∴4−2a+2−a=6−3a =3,∴a =1,∴O(1,0),
P在空间内轨迹为以O为球心半径为2的球,
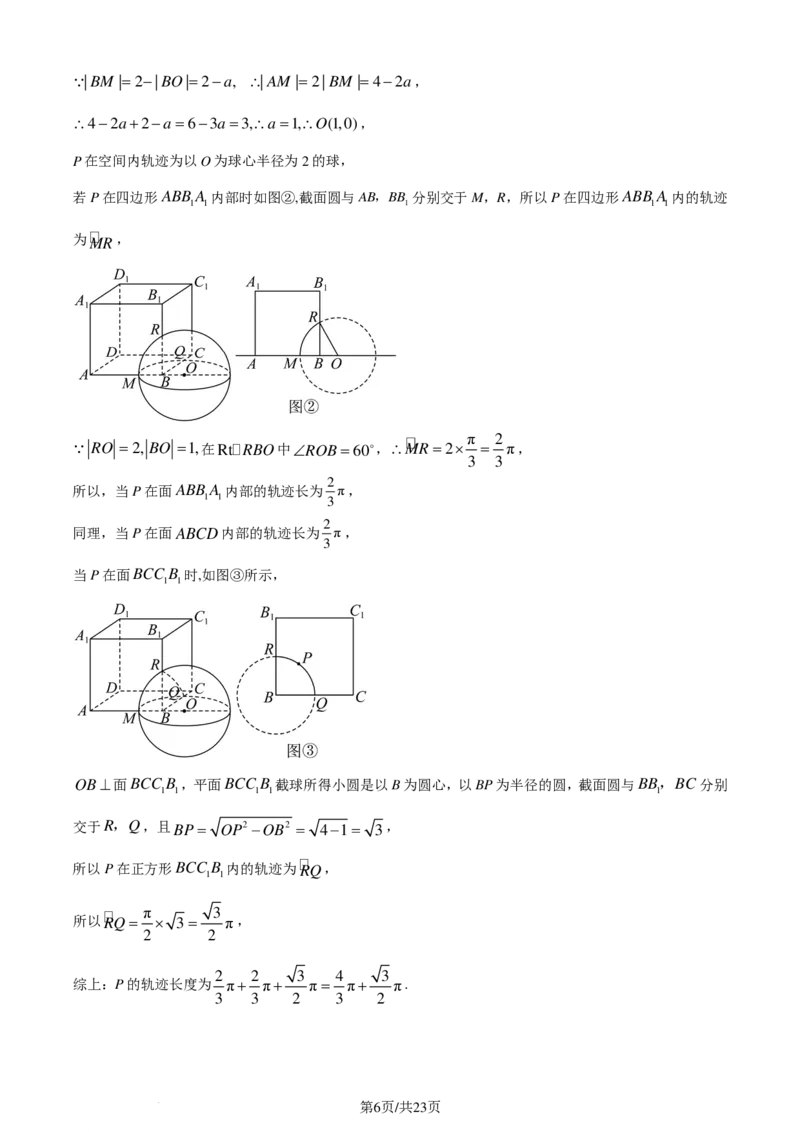
若P在四边形ABB A 内部时如图②,截面圆与AB,BB 分别交于M,R,所以P在四边形ABB A 内的轨迹
1 1 1 1 1
为
M
R
,
π 2
RO =2, BO =1,在RtRBO中∠ROB=60,∴MR=2× = π,
3 3
2
所以,当P在面ABB A 内部的轨迹长为 π,
1 1 3
2
同理,当P在面ABCD内部的轨迹长为 π,
3
当P在面BCC B 时,如图③所示,
1 1
OB⊥面BCC B ,平面BCC B 截球所得小圆是以B为圆心,以BP为半径的圆,截面圆与BB,BC分别
1 1 1 1 1
交于R,Q,且BP= OP2 −OB2 = 4−1= 3,
所以P在正方形BCC B 内的轨迹为RQ,
1 1
π 3
所以RQ= × 3 = π,
2 2
2 2 3 4 3
综上:P的轨迹长度为 π+ π+ π= π+ π.
3 3 2 3 2
第6页/共23页
学科网(北京)股份有限公司故选:C
【点睛】方法点睛:求球与平面公共点轨迹长度时先求出平面截球所得圆面的半径,当截面为完整的圆时可
直接求圆周长,当截面只是圆的一部分时先求圆心角的大小再计算弧长.
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 已知复数z =1−i,z = x+ yi ( x,y∈R ) ,则下列结论正确的是( )
0
A. 方程 z−z =2表示的z在复平面内对应点的轨迹是圆
0
B. 方程 z−z + z−z =2表示的z在复平面内对应点的轨迹是椭圆
0 0
C. 方程 z−z − z−z =1表示的z在复平面内对应点的轨迹是双曲线的一支
0 0
1( )
D. 方程 z+ z +z = z−z 表示的z在复平面内对应点的轨迹是抛物线
2 0 0 0
【答案】AC
【解析】
【分析】根据复数模的几何意义,及椭圆、双曲线的定义逐项分析即可.
【详解】由复数模的几何意义知,
z−z =2表示复平面内点(x,y)与点(1,−1)之间的距离为定值2,
0
则z在复平面内对应点的轨迹是圆,故A正确;
由复数模的几何意义知,
z−z + z−z =2表示复平面内点(x,y)到点(1,−1)和(1,1)的距离之和为2,
0 0
又2= z −z ,不满足椭圆的定义2a> FF ,故B不正确;
0 0 1 2
由复数模的几何意义知,
z−z − z−z =1表示复平面内点(x,y)到点(1,−1)和(1,1)的距离之差为1,
0 0
又2= z −z ,满足双曲线的定义2a < FF ,故C正确;
0 0 1 2
1( )
对于D, z+ z +z = z−z 可化为 z+1 = z−z ,
2 0 0 0 0
表示复平面内点(x,y)到点(−1,0)和(1,−1)的距离相等,轨迹是直线,
故D不正确,
第7页/共23页
学科网(北京)股份有限公司故选:AC.
10. 已知θ为锐角,则下列说法错误的是( )
A. 满足tanθ=cosθ+sinθ的θ值有且仅有一个
B. 满足sinθ,tanθ,cosθ成等比数列的θ值有且仅有一个
C. sinθ,cosθ,tanθ三者可以以任意顺序构成等差数列
D. 存在θ使得tanθ−sinθ,cosθ−sinθ,cosθ−tanθ成等比数列
【答案】CD
【解析】
【分析】从前往后的顺序,利用三角函数公式,图象和性质,逐步判断,找到错误的C,利用反证法可判
断D的正误.
π π
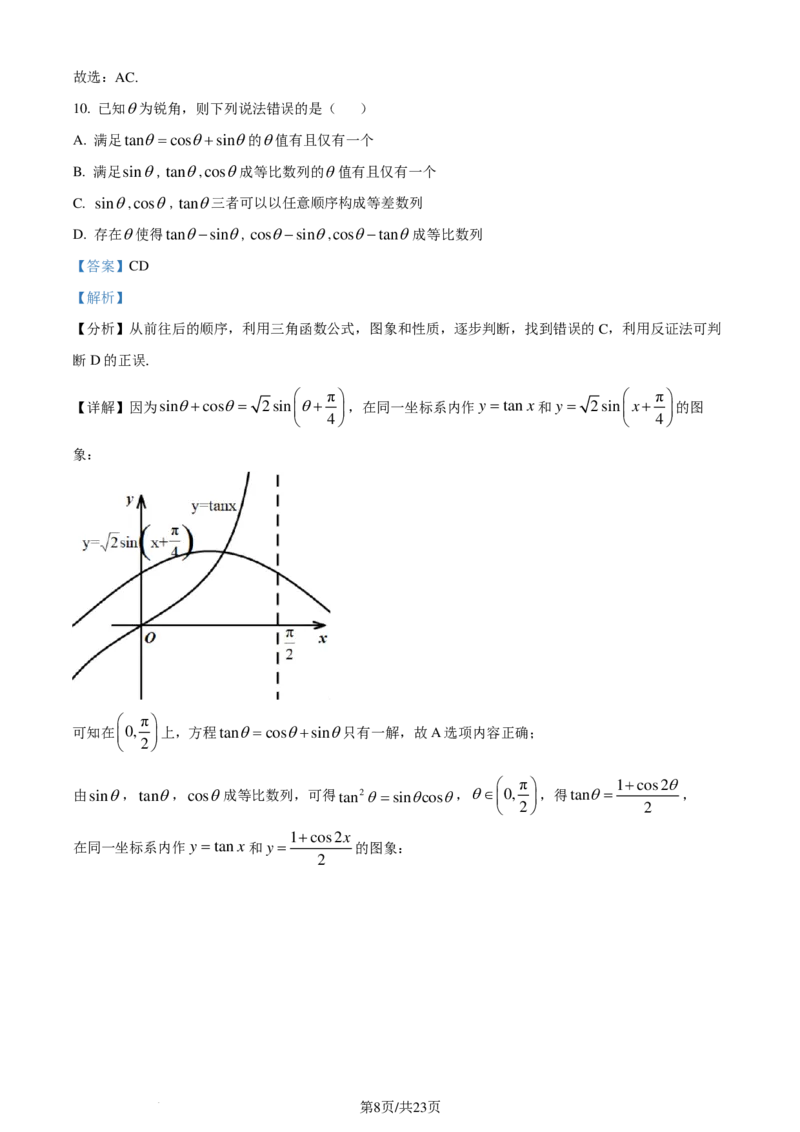
【详解】因为sinθ+cosθ= 2sin θ+ ,在同一坐标系内作y = tanx和 y = 2sinx+ 的图
4 4
象:
π
可知在0, 上,方程tanθ=cosθ+sinθ只有一解,故A选项内容正确;
2
π 1+cos2θ
由sinθ,tanθ,cosθ成等比数列,可得tan2θ=sinθcosθ,θ∈ 0, ,得tanθ= ,
2 2
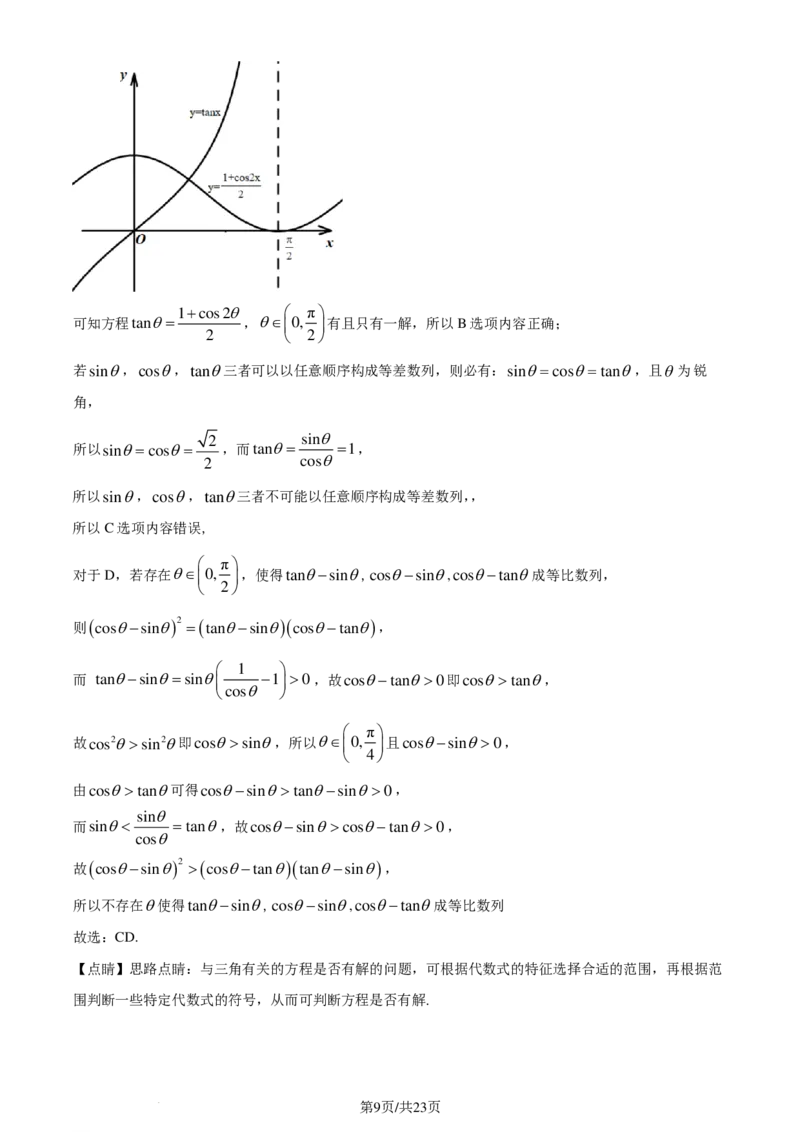
1+cos2x
在同一坐标系内作y = tanx和y = 的图象:
2
第8页/共23页
学科网(北京)股份有限公司1+cos2θ π
可知方程tanθ= ,θ∈ 0, 有且只有一解,所以B选项内容正确;
2 2
若sinθ,cosθ,tanθ三者可以以任意顺序构成等差数列,则必有:sinθ=cosθ=tanθ,且θ 为锐
角,
2 sinθ
所以sinθ=cosθ= ,而tanθ= =1,
2 cosθ
所以sinθ,cosθ,tanθ三者不可能以任意顺序构成等差数列,,
所以C选项内容错误,
π
对于D,若存在θ∈ 0, ,使得tanθ−sinθ,cosθ−sinθ,cosθ−tanθ成等比数列,
2
则( cosθ−sinθ)2 =( tanθ−sinθ)( cosθ−tanθ),
1
而 tanθ−sinθ=sinθ −1 >0,故cosθ−tanθ>0即cosθ>tanθ,
cosθ
π
故cos2θ>sin2θ即cosθ>sinθ,所以θ∈ 0, 且cosθ−sinθ>0,
4
由cosθ>tanθ可得cosθ−sinθ>tanθ−sinθ>0,
sinθ
而sinθ< =tanθ,故cosθ−sinθ>cosθ−tanθ>0,
cosθ
故( cosθ−sinθ)2 >( cosθ−tanθ)( tanθ−sinθ),
所以不存在θ使得tanθ−sinθ,cosθ−sinθ,cosθ−tanθ成等比数列
故选:CD.
【点睛】思路点睛:与三角有关的方程是否有解的问题,可根据代数式的特征选择合适的范围,再根据范
围判断一些特定代数式的符号,从而可判断方程是否有解.
第9页/共23页
学科网(北京)股份有限公司11. 已知无穷数列 { a } ,a =1.性质s:∀m,n∈N*,a >a +a ,;性质t:∀m,n∈N*,
n 1 m+n m n
2≤ma +a ,下列说法中正确的有( )
m−1 n+1 m n
A. 若a =3−2n,则 { a } 具有性质s
n n
B. 若a =n2,则 { a } 具有性质t
n n
C. 若 { a } 具有性质s,则a ≥n
n n
D. 若等比数列
{
a
}
既满足性质s又满足性质t,则其公比的取值范围为
( 2,+∞)
n
【答案】BCD
【解析】
【分析】根据性质s的定义可判断选项A;根据性质t的定义可判断选项B;根据性质s的定义可得
a −a >1,n≥2,n∈N*,利用累加法可证选项C;对于D,结合选项C,可得q >1,由 { a } 满足性
n n−1 n
质s,分m=n和m≠n讨论求出q>2,再由 { a } 满足性质t得qn −qn−1 >qm−1−qm−2,令
n
f ( x )=qx −qx−1,结合函数单调性可验证q>2满足题意.
【详解】对于A,因为a =3−2n,对∀m,n∈N*,
n
a −a −a =3−2 ( m+n )−( 3−2m )−( 3−2n )=−3<0,
m+n m n
即a 0,
m−1 n+1 m n
∴a +a >a +a ,故B正确;
m−1 n+1 m n
对于C,若 { a } 具有性质s,令m=1,则a >a +a =1+a ,
n n+1 1 n n
即a −a >1,n≥2,n∈N*,
n n−1
∴a =( a −a )+( a −a )+…+( a −a )+a >1+1+…+1=n,又a =1,
n n n−1 n−1 n−2 2 1 1 1
所以a ≥n,n∈N*,故C正确;
n
对于D, { a } 是等比数列,设其公比为q,又a =1,∴a =qn−1,
n 1 n
若 { a } 满足性质s,由选项C 得a ≥n,即qn−1 ≥n,n∈N*,∴q >1,
n n
第10页/共23页
学科网(北京)股份有限公司由∀m,n∈N*,a >a +a ,得qm+n >qm +qn,
m+n m n
当m=n时,得q2n >2qn,即qn >2,对∀n∈N*,又qn ≥q,∴q >2,
当m≠n时,不妨设n>m≥1,则qn >qm ≥q,
∴qm+n >qm +qn >2qm,解得qn >2,∴q≥2,
综上,若 { a } 满足性质s,则q>2.
n
若 { a } 满足性质t,对∀m,n∈N*,2≤ma +a ,
n m−1 n+1 m n
可得qm−2 +qn >qm−1+qn−1,即qn −qn−1 >qm−1−qm−2,令 f ( x )=qx −qx−1,则 f ( n )> f ( m−1 ) ,
又n>m−1,所以函数 f ( x )=qx −qx−1在x∈N*上单调递增,又由 { a } 满足性质s,q>2,
n
∴ f′( x )=qxlnq−qx−1lnq=qx−1⋅lnq⋅( q−1 )>0成立,
所以等比数列
{
a
}
既满足性质s又满足性质t,则其公比的取值范围为
( 2,+∞)
.
n
故D正确.
故选:BCD.
【点睛】思路点睛:选项C,由题意可得a −a >1,n≥2,n∈N*,累加法可得
n n−1
a =( a −a )+( a −a )+…+( a −a )+a >n,结合a =1,可判断;选项D,由 { a } 满足性质
n n n−1 n−1 n−2 2 1 1 1 n
s,结合选项C得q >1,分m=n和m≠n讨论恒成立求出q>2,又由 { a } 满足性质t,得
n
qn −qn−1 >qm−1−qm−2,令 f ( x )=qx −qx−1,结合函数单调性可验证q>2满足题意.
三、填空题:本题共 3小题,每小题 5分,共 15分.
12. 已知 p:−3≤ x≤1,q:xa(a为实数).若 q的一个充分不必要条件是 p,则实数 a的取值范围是
________.
【答案】
[ 1,+∞)
【解析】
【分析】利用小范围是大范围的充分不必要条件转换成集合的包含关系求解.
【详解】因为q的一个充分不必要条件是p,
所以[−3,1]是(−∞,a ]的一个真子集,
则a≥1,即实数a的取值范围是
[ 1,+∞)
.
第11页/共23页
学科网(北京)股份有限公司故答案为:
[ 1,+∞)
.
13. 各棱长均为1且底面为正方形的平行六面体ABCD−ABC D ,满足∠AAB=∠AAD=60°,则
1 1 1 1 1 1
AC =______;此平行六面体的体积为______.
1
2
【答案】 ①. 5 ②.
2
【解析】
【分析】由空间向量基本定理可得AC = AB+BB +BC ,对其两边同时平方结合数量积的定义即可求出
1 1
AC ;连接AB,CD交于点O,连接AO,先证明AO⊥平面ABCD,再由柱体的体积公式即可得出答
1 1 1
案.
2 2 2 2
【详解】因为AC =(AB+BB +BC)2 = AB +BB +BC +2AB⋅BB +2AB⋅BC+2BB ⋅BC
1 1 1 1 1
=1+1+1+2 AB ⋅ BB cos∠AAB+2 AB ⋅ BC cos∠DAB+2 BB ⋅ BC cos∠CBB
1 1 1 1
1 1
=3+2×1×1× +0+2×1×1× =5,
2 2
所以 AC = 5.
1
连接AB,CD交于点O,连接AO,
1
1 2 1 2
因为底面为边长是1的正方形,所以 AO = AC = , DO = BD =
2 2 2 2
因为∠AAB=∠AAD=60°,连接AD,AB,则 AD = AB =1,
1 1 1 1 1 1
2
所以在△ADB中,AO ⊥ BD,所以 AO = AD 2 − DO 2 = ,
1 1 1 1 2
又因为 AO 2 + AO 2 = AA 2,所以AO⊥ AO,
1 1 1
AOBD=O,AO,BD⊂平面ABCD,
所以AO⊥平面ABCD,所以平行六面体的体积为:
1
第12页/共23页
学科网(北京)股份有限公司2 2
V =S ⋅AO=1× = .
ABCD 1 2 2
2
故答案为: 5; .
2
14. 已知定义在R上的增函数 f(x)满足对任意的x,x ∈R都有 f(x +x )= f(x )f(x ),且
1 2 1 2 1 2
f(3)=8,函数g(x)满足g(x)+g(4−x)=4,g(6−x)= g(x),且当x∈[ 2,3 ] 时g(x)= f(x−1).若
g(x)在 [ 0,100 ] 上取得最大值的x值依次为x,x,…,x ,取得最小值的x值依次为x′,x′,…,
1 2 k 1 2
k n
x′,则∑
x +g ( x )
+∑
x′+g ( x′)
=______.
n i i i i
i=1 i=1
【答案】2600
【解析】
【分析】对 f ( x ) 可得 f(1)=2, f(2)=4,由题意分析可知g(x)的一个周期为4,关于点(2,2)对称,关
于直线x=3对称,进而结合函数性质分析求解.
【详解】因为 f(x +x )= f(x )f(x ),
1 2 1 2
令x
1
= x
2
= x,可得 f ( 2x )=
f ( x )
2 ,
令x
1
=2x,x
2
= x,可得 f ( 3x )= f ( 2x ) f ( x )=
f ( x )
3 ,
因为 f(3)=8,所以 f(1)=2, f(2)=4.
因为g(x)+g(4−x)=4,可知g(x)的图象关于点(2,2)对称,
又因为当x∈[2,3]时,g(x)= f(x−1),则g(x)在 [ 2,3 ] 上单调递增,且g(3)= f(2)=4,
所以g(x)在[
1,2
]上单调递增,且g(1)=0.
因为g(6−x)= g(x),则g(x)的图象关于直线x=3对称,
所以g(x)在(3,5]上单调递减,且g(5)=0,
第13页/共23页
学科网(北京)股份有限公司故g(x)在[1,5]上的最大值为4,最小值为0.
由g(6−x)= g(x)得g(4−x)= g(x+2),则g(x)+g(x+2)=4,
所以g(x+2)+g(x+4)=4,得g(x+4)= g(x),
故g(x)的一个周期为4,且在x=4m−3(m∈Z)处取得最小值0,在x =4m−1处取得最大值4,
k n
所以∑
x +g ( x )
+∑
x′+g ( x′)
=3+7+11+⋅⋅⋅+99+25×4+1+5+9+⋅⋅⋅+97+25×0=2600.
i i i i
i=1 i=1
故答案为:2600.
【点睛】方法点睛:函数的性质主要是函数的奇偶性、单调性和周期性以及函数图象的对称性,在解题中根
据问题的条件通过变换函数的解析式或者已知的函数关系,推证函数的性质,根据函数的性质解决问题.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
a
15. 已知函数 f ( x )=lnx+ x2 −( a+1 ) x,g ( x ) = −ax2 +( a+1 ) x.
2
( )
(1)讨论函数 f x 的单调性;
(2)若 f
(
x
)+g (
x
)≤0恒成立,求a的取值范围.
【答案】15. 答案见解析
1
16. ,+∞
e
【解析】
1
【分析】(1)根据题意求出对函数 f ( x ) 求导得 f′( x )= +ax−( a+1 ),然后分类对a进行讨论,从而可
x
求解.
(2)由 f ( x )+g ( x )≤0恒成立,利用参数分离可得a≥ 2lnx = lnx2 ,然后构造函数h ( t )= lnt ,再
x2 x2 t
( )
利用导数求解出h t 的最大值,从而可求解.
【小问1详解】
1
由题意知: f′( x )= +ax−( a+1 ),x∈( 0,+∞)
x
ax2 −( a+1 ) x+1 ( x−1 )( ax−1 )
所以 f′( x )= = ,x∈( 0,+∞)
x x
①当a∈(−∞,0 ] 时,若x∈( 0,1 ) ,则 f′(x)>0,若x∈( 1,+∞) ,则 f′(x)<0,
第14页/共23页
学科网(北京)股份有限公司所以 f(x)在
(
0,1
)
上单调递增, f(x)在
( 1,+∞)
上单调递减;
1 1
②当a∈( 0,1 ) 时,令 f′(x)=0得:x=1或x= ,且 >1,
a a
1 1
若x∈( 0,1 ) ,则 f′( x )>0,若x∈ 1, ,则 f′( x )<0,若x∈ ,+∞ ,则 f′( x )>0,
a a
1 1
所以 f(x)在 ( 0,1 ) , ,+∞ 上单调递增,在1, 上单调递减;
a a
③当a =1时, f′(x)≥0恒成立,所以 f(x)在 ( 0,+∞) 上单调递增;
1 1
④当a∈( 1,+∞) 时,令 f′(x)=0得:x=1或x= ,且0< <1,
a a
1 1
若x∈ 0, ,则 f′( x )>0,若x∈ ,1,则 f′( x )<0,若x∈( 1,+∞) ,则 f′( x )>0,
a a
1 1
所以 f(x)在0, ,
( 1,+∞)
上单调递增,在 ,1上单调递减.
a a
【小问2详解】
a
由 f(x)+g(x)≤0恒成立,即lnx− x2 ≤0,x∈( 0,+∞) 恒成立,
2
所以a ≥
2lnx
=
lnx2 ,x∈( 0,+∞)
,
x2 x2
lnt 1−lnt
令h(t)= ,t∈( 0,+∞) ,所以h′(t)= ,
t t2
若t∈(
0,e
) ,则h′(
t
)>0,若t∈( e,+∞) ,则h′(
t
)<0,
h(t)在
(
0,e
)
上单调递增,在
( e,+∞)
上单调递减;
1 1
所以当t =e时,h(t)有极大值也是最大值为h(e)= ,所以a≥ .
e e
1
所以a的取值范围为 ,+∞ .
e
16. 有两个盒子,其中1号盒子中有3个红球,2个白球;2号盒子中有6个红球,4个白球.现按照如下
规则摸球.从两个盒子中任意选择一个盒子,再从盒中随机摸出2个球,摸球的结果是一红一白.
(1)你认为较大可能选择的是哪个盒子?请做出你的判断,并说明理由;
(2)如果你根据(1)中的判断,面对相同的情境,作出了5次同样的判断,记判断正确的次数为X,求
第15页/共23页
学科网(北京)股份有限公司X的数学期望(实际选择的盒子与你认为较大可能选择的盒子相同时,即为判断正确).
【答案】(1)选择1号盒子
45
(2)
17
【解析】
【分析】(1)计算出1号盒子和2号盒子中摸出一红一白的概率比较下结论;
9
(2)根据题意得到X B5, 求解.
17
【小问1详解】
解:设选择1号盒子后摸出一红一白的概率为P,
1
设选择2号盒子后摸出一红一白的概率为P ,
2
C1C1 3 C1C1 8
则 P = 3 2 = , P = 6 4 = ,
1 C2 5 2 C2 15
5 10
因为 P > P ,
1 2
所以较大可能选择1号盒子;
【小问2详解】
1
P
2 1 9
由贝叶斯公式,选择1号盒子后猜中的概率P= =
1 1 17
P + P
2 1 2 2
9
由题意得:X B5, ,
17
9 45
所以E ( X )=5× = .
17 17
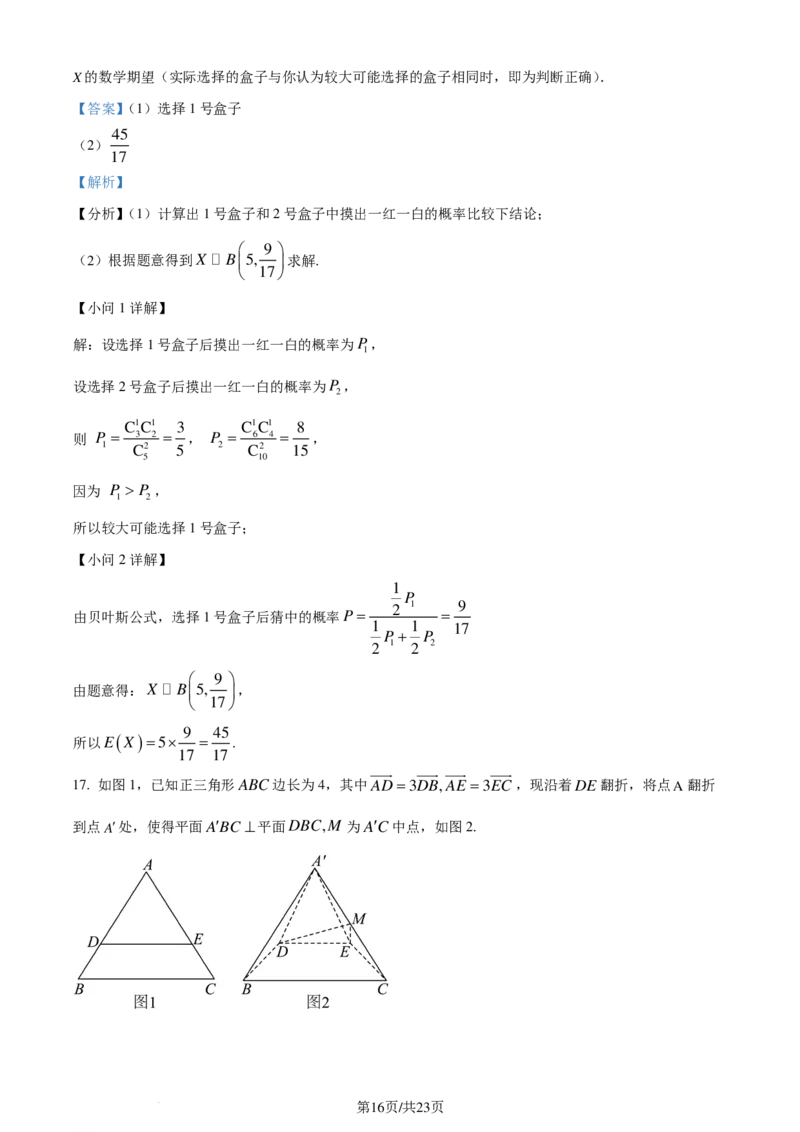
17. 如图1,已知正三角形ABC边长为4,其中AD=3DB,AE =3EC,现沿着DE翻折,将点A翻折
到点A′处,使得平面A′BC ⊥平面DBC,M 为A′C中点,如图2.
第16页/共23页
学科网(北京)股份有限公司(1)求异面直线A′D与EM 所成角的余弦值;
(2)求平面A′BC与平面DEM 夹角的余弦值.
10
【答案】(1)
5
6
(2)
3
【解析】
【分析】(1)设O为BC的中点,结合图形翻折的性质推出A′O ⊥平面DBC,建立空间直角坐标系,求
得相关线段长,即可求出相关点坐标,利用空间角的向量求法,即可求得异面直线A′D与EM 所成角的
余弦值;
(2)求出平面A′BC与平面DEM 的法向量,根据空间角的向量求法,即可求得答案.
【小问1详解】
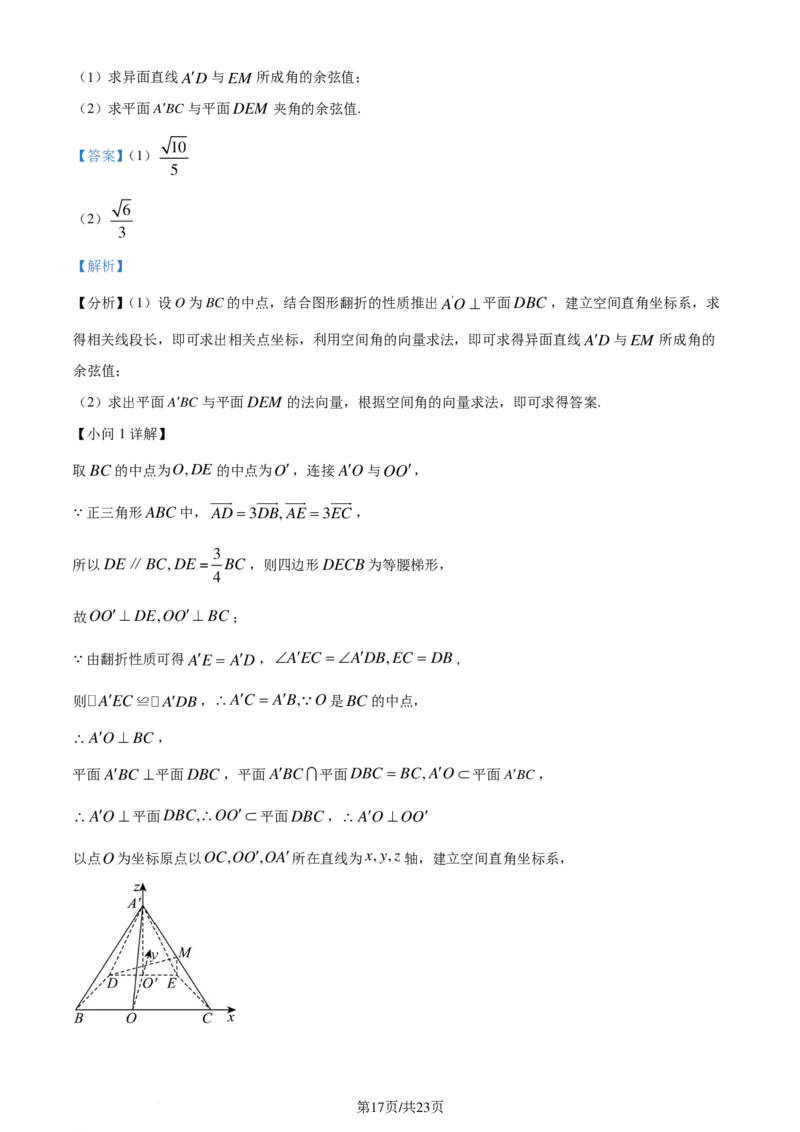
取BC的中点为O,DE的中点为O′,连接A′O与OO′,
正三角形ABC中,AD=3DB,AE =3EC,
3
所以DE∥BC,DE = BC,则四边形DECB为等腰梯形,
4
故OO′⊥ DE,OO′⊥ BC;
由翻折性质可得A′E = A′D,∠A′EC =∠A′DB,EC = DB,
则A′EC≌A′DB,∴A′C = A′B,O是BC的中点,
∴A′O⊥ BC,
平面A′BC ⊥平面DBC,平面A′BC平面DBC = BC,A′O⊂平面A′BC,
∴A′O⊥平面DBC,∴OO′⊂平面DBC,∴A′O⊥OO′
以点O为坐标原点以OC,OO′,OA′所在直线为x,y,z轴,建立空间直角坐标系,
第17页/共23页
学科网(北京)股份有限公司3
正ABC的边长为4,DE∥BC,DE = BC,
4
3 3
则A′DE为正三角形,边长为3,则A′O′⊥ DE,∴A′O′= ,
2
3
OC =OB=2,OO′= ,连接A′O′,
2
3 3 3
在A′OO′中,由勾股定理得OA′= ( )2 −( )2 = 6 ,
2 2
( ) 3 3 3 3 6
∴A′ 0,0, 6 ,D− , ,0,E , ,0,C(2,0,0),M 1,0, ,
2 2 2 2 2
3 3 1 3 6
则A′D=− , ,− 6,EM =− ,− , ,
2 2 2 2 2
A′D⋅EM −3 10
∴cos〈A′D,EM〉 = = =−
A′D ⋅ EM 5 5 ,
3⋅
2
π
异面直线所成角的取值范围为(0, ],
2
10
∴异面直线A′D与EM 所成角的余弦值为 .
5
【小问2详解】
( ) 3 3
由(1)得A′ 0,0, 6 ,B (−2,0,0 ) ,C ( 2,0,0 ) ,D− , ,0,
2 2
3 3 6
E , ,0,M 1,0, ,
2 2 2
5 3 6
∴DE =( 3,0,0 ) ,DM = ,− , ,
2 2 2
易得平面A′BC的一个法向量为m=(
0,1,0
)
,
设平面DEM 的法向量为n
=(
x,y,z
)
,
3x=0
DE⋅n =0 ( )
则
,即5
3 6
,令z =1,则n = 0, 2,1 ,
DM ⋅n =0 x− y+ z =0
2 2 2
第18页/共23页
学科网(北京)股份有限公司
m⋅n 2 6
∴cos〈m,n〉 = = = ,
m ⋅ n 1× 3 3
6
∴平面A′BC与平面DEM 夹角的余弦值为 .
3
4
18. 在平面直角坐标系xOy中,已知抛物线C:y2 =2px(p>0)和点R(4,5).点P在C上,且OP = OR.
5
(1)求C的方程;
(2)若过点R作两条直线l 与l ,l 与C相交于A,B两点,l 与C相交于E,D两点,线段AB和
1 2 1 2
ED中点的连线的斜率为k,直线AB,ED,AD,BE 的斜率分别为k ,k ,k ,k ,证明:
1 2 3 4
1 1 1 1 1 1 1
+ = + ,且 + − 为定值.
k k k k k k k
1 2 3 4 3 4
【答案】(1) y2 =5x
(2)证明见解析
【解析】
4
【分析】(1)由己知,根据R点坐标,借助OP = OR可表示出P点坐标,然后带入抛物线方程,即可
5
完成方程的求解;
(2)由已知,分别设出A,B,C,D四点坐标,然后利用坐标分别表示出直线AB,ED,AD,BE的斜
1 1 1 1
率,即可证得 + = + ,设AB和ED的中点分别为M ,N ,分别联立l ,l 与抛物线方程,
k k k k AB CD
1 2 3 4
1
求得M ,N 的坐标,利用斜率公式表示 ,化简计算即可得出结果.
k
【小问1详解】
4
设点P ( x ,y ) ,则OP=( x ,y ),因为OP = OR,OR =(4,5),
0 0 0 0 5
4 16 4 16
所以x = ×4 = ,y = ×5= 4,所以点P ,4,
0 5 5 0 5 5
5
代入方程y2 =2px中,得 p= ,所以C的方程为 y2 =5x.
2
【小问2详解】
( ) ( ) ( ) ( )
设点A x ,y ,B x ,y ,E x ,y ,D x ,y ,
1 1 2 2 3 3 4 4
第19页/共23页
学科网(北京)股份有限公司y − y 5
则直线AB的斜率k = 1 2 = ,
1 x −x y + y
1 2 1 2
y − y 5
同理得直线ED的斜率k = 4 3 = ,
2 x −x y + y
4 3 3 4
y − y 5
直线AD的斜率k = 4 1 = ,
3 x −x y + y
4 1 1 4
y − y 5
直线BE的斜率k = 3 2 = ,
4 x −x y + y
3 2 2 3
1 1 y + y y + y 1
所以 + = 1 2 + 3 4 = ( y + y + y + y ) ,
k k 5 5 5 1 2 3 4
1 2
1 1 y + y y + y 1
+ = 1 4 + 2 3 = ( y + y + y + y ) ,
k k 5 5 5 1 2 3 4
3 4
1 1 1 1
从而得 + = + .
k k k k
1 2 3 4
y−5=k ( x−4 ) ,
由 1 消去x得k y2 −5y+5 ( 5−4k )=0,
y2 =5x, 1 1
5 5 ( 5−4k )
所以y + y = , y y = 1
1 2 k 1 2 k
1 1
由Δ=25−20k ( 5−4k )>0,得k > 5+ 5 或k < 5− 5 .
1 1 1 8 1 8
设AB和ED的中点分别为M ,N ,
1 5 y −5 5−10k
则y = ( y + y )= ,x = M +4= 1 +4,
M 2 1 2 2k M k 2k2
1 1 1
5 5−10k
同理y = ,x = 2 +4,
N 2k N 2k 2
2 2
5 1 1 1 1
− −5 −
1 x −x 2k2 k 2 k k 1 1 1 1 1
所以 = M N = 1 2 1 2 = + −2,即 + − = 2,
k y − y 5 1 1 k k k k k
M N − 1 2 1 2
2k k
1 2
1 1 1 1 1 1
所以得 + − = + − = 2.
k k k k k k
3 4 1 2
第20页/共23页
学科网(北京)股份有限公司19. 若存在x ∈D使得 f ( x )≤ f ( x ) 对任意x∈D恒成立,则称x 为函数 f ( x ) 在D上的最大值点,记函
0 0 0
( )
数 f x 在D上的所有最大值点所构成的集合为M
(1)若 f ( x )=−x2 +2x+1,D=R,求集合M ;
( )
2x −x x
(2)若 f ( x )= ,D=R ,求集合M ;
4x
(3)设a为大于1的常数,若 f
(
x
)= x+asinx,D=[
0,b
]
,证明,若集合M 中有且仅有两个元素,则
所有满足条件的b从小到大排列构成一个等差数列.
【答案】(1)M
={
1
}
(2)M
={
1,2
}
(3)证明见解析
【解析】
【分析】(1)配方得到当且仅当x=1时, f ( x )=−x2 +2x+1取得最大值,得到M ={ 1 } ;
(2)求导,得到函数单调性,求出当x=1或2时, f
(
x
)
取得最大值,故M
={
1,2
}
;
1
(3)求导,得到函数单调性,并得到 f′( x+2π )= f′( x ) ,得到 f ( b )= f 2kπ−π−arccos ,结合
k a
f ( b )− f ( b )=2π,得到b −b 为定值,
k+1 k k+1 k
故所有满足条件的b从小到大排列构成一个等差数列.
【小问1详解】
f ( x )=−x2 +2x+1=−( x−1 )2 +2,
当且仅当x=1时, f ( x )=−x2 +2x+1在R上取得最大值,故M ={ 1 } ;
【小问2详解】
( )
2x −x x
f ( x )= 定义域为R,
4x
( 2xln2−1 ) x+2x −x4x − ( 2x −x ) x⋅4xln4
f′(
x
)=
42x
( 2x −2x )( 1−xln2 )
= ,
4x
第21页/共23页
学科网(北京)股份有限公司令q
(
x
)=2x −2x,则q′(
x
)=2xln2−2,
2
令q′(
x
)=0得x=log
,
2 ln2
2 2 2
x −∞,log log log ,+∞
2 ln2 2 ln2 2 ln2
q′(
x
)
- 0 +
( )
q x 极小值
( ) 1 2 2
其中ln2∈ ln e,lne = ,1,故 ∈( 2,4 ),log ∈( 1,2 ),
2 ln2 2 ln2
可以看出q
(
1
)=0,q (
2
)=0,
( )
故q x 有且仅有2个零点,分别为1和2,
1
令 f′( x )=0得x= ∈( 1,2 )或1或2,
ln2
1 1 1
x (−∞,1 ) 1 1, ,2 2 (2,+∞)
ln2 ln2 ln2
f
′(
x
)
+ 0 - 0 + 0 -
( )
f x 极大值 极小值 极大值
1
其中 f ( 1 )= f ( 2 )= ,
4
故当x=1或2时, f
(
x
)
取得最大值,故M
={
1,2
}
;
【小问3详解】
f
(
x
)= x+asinx,D=[
0,b
]
,a >1,
f′(
x
)=1+acosx,D=[
0,b
]
,a >1,
1 1
令 f′( x )=0得x=2kπ±arccos − =2kπ± π−arccos ,k∈Z,
a a
1
当0< x<π−arccos 时, fx0, f ( x ) 单调递增,
a
第22页/共23页
学科网(北京)股份有限公司1 1
当π−arccos < x<π+arccos 时, f′(x)<0, f ( x ) 单调递减,
a a
1 1
当π+arccos < x<3π−arccos 时, fx0, f ( x ) 单调递增,
a a
1 1
当3π−arccos < x<3π+arccos 时, f′(x)<0, f ( x ) 单调递减,
a a
1 1
当3π+arccos < x<5π−arccos , fx0, f ( x ) 单调递增,
a a
……,
由于 f′( x+2π )=1+acos ( x+2π )=1+acosx= f′( x ) ,
故所有的单调递增区间经过适当平移可重合,同理,所有的单调递减区间经过适当平移可重合,
要想集合M 中有且仅有两个元素,
1 1
则需要 f ( b )= f π−arccos 或 f ( b )= f 3π−arccos ,
1 a 2 a
1 1
或 f ( b )= f 5π−arccos ,……, f ( b )= f 2kπ−π−arccos ,
3 a k a
其中 f ( x+2π )= x+2π+asin ( x+2π )= x+2π+asinx,
f ( x+2π )− f ( x )= x+2π+asinx−x−asinx=2π,
1 1
又 f ( b )− f ( b )= f 2kπ+2π−π−arccos − f 2kπ−π−arccos =2π,
k+1 k a a
所有的b 均处在单调递增区间上,
k
所以b −b 为定值,
k+1 k
故所有满足条件的b从小到大排列构成一个等差数列.
【点睛】函数新定义问题,命题新颖,且存在知识点交叉,常常会和函数的性质,包括单调性,值域等进行
结合,很好的考虑了知识迁移,综合运用能力,对于此类问题,一定要解读出题干中的信息,正确理解问题
的本质,转化为熟悉的问题来进行解决.
第23页/共23页
学科网(北京)股份有限公司