文档内容
南昌二中 2024 届高三“九省联考”考后适应性测试数学试题一
本套试卷根据九省联考题型命制,题型为 8+3+3+5模式
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 数据6.0,7.4,8.0,8.4,8.6,8.7,9.0,9.1的50百分位数为( )
A. 8.4 B. 8.5 C. 8.6 D. 8.7
x2
2. 已知双曲线C: y2 − =1(b>0)的离心率e< 2,则b的取值范围是( )
b2
A. (0,1) B. (1, 2) C. (1,+∞) D. ( 2,+∞)
1
3. 若数列 { a } 满足a =11,a = ,则a =( )
n 2 n+1 1−a 985
n
11 1 10
A. B. 11 C. − D.
10 10 11
4. 已知平面α,β,直线l⊂α,直线m不在平面α上,下列说法正确的是( )
A. 若α//β,m//β,则l//m B. 若α//β,m⊥β,则l ⊥m
C. 若l//m,α//β,则m//β D. 若l ⊥m,m//β,则α⊥β
5. 在某次美术专业测试中,若甲、乙、丙三人获得优秀等级的概率分别是0.6,0.7和0.5,且三人的测试
结果相互独立,则测试结束后,在甲、乙、丙三人中恰有两人没达优秀等级的前提条件下,乙没有达优秀
等级的概率为( )
15 7 5 17
A. B. C. D.
29 8 8 29
6. 在平面直角坐标系中,集合A= {( x,y ) kx− y+k =0 } ,集合B= {( x,y ) y =kx−1 } ,已知点
M∈A,点N∈B,记d表示线段MN 长度的最小值,则d的最大值为( )
A. 2 B. 3 C. 1 D. 2
π π
7. 已知函数 f(x)=cos2x,g(x)=sinx,则存在θ∈ , ,使得( )
6 4
A. 2g(θ)= f(θ)+g(θ)⋅ f(θ) B. 4g(θ)⋅ f(θ)= f(θ)+2g(θ)
C. 2f(θ)= g(θ)+g(θ)⋅ f(θ) D. f(θ)= g(θ)
第1页/共4页
学科网(北京)股份有限公司PA
8. 已知平面上两定点A、B,则所有满足 =λ(λ>0且λ≠1)的点P的轨迹是一个圆心在AB上,
PB
λ
半径为 ⋅ AB 的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称作阿氏圆.已知棱长为3的正
1−λ2
方体ABCD−ABC D 表面上动点P满足 PA =2 PB ,则点P的轨迹长度为( )
1 1 1 1
4π 4π 3π ( )
A. 2π B. + 3π C. + D. 2+ 3 π
3 3 2
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 已知复数z =1−i,z = x+ yi ( x,y∈R ) ,则下列结论正确的是( )
0
A. 方程 z−z =2表示的z在复平面内对应点的轨迹是圆
0
B. 方程 z−z + z−z =2表示的z在复平面内对应点的轨迹是椭圆
0 0
C. 方程 z−z − z−z =1表示的z在复平面内对应点的轨迹是双曲线的一支
0 0
1( )
D. 方程 z+ z +z = z−z 表示的z在复平面内对应点的轨迹是抛物线
2 0 0 0
10. 已知θ为锐角,则下列说法错误的是( )
A. 满足tanθ=cosθ+sinθ的θ值有且仅有一个
B. 满足sinθ,tanθ,cosθ成等比数列的θ值有且仅有一个
C. sinθ,cosθ,tanθ三者可以以任意顺序构成等差数列
D. 存在θ使得tanθ−sinθ,cosθ−sinθ,cosθ−tanθ成等比数列
11. 已知无穷数列 { a } ,a =1.性质s:∀m,n∈N*,a >a +a ,;性质t:∀m,n∈N*,
n 1 m+n m n
2≤ma +a ,下列说法中正确的有( )
m−1 n+1 m n
A. 若a =3−2n,则 { a } 具有性质s
n n
B. 若a =n2,则 { a } 具有性质t
n n
C. 若 { a } 具有性质s,则a ≥n
n n
D. 若等比数列
{
a
}
既满足性质s又满足性质t,则其公比的取值范围为
( 2,+∞)
n
三、填空题:本题共 3小题,每小题 5分,共 15分.
第2页/共4页
学科网(北京)股份有限公司12. 已知 p:−3≤ x≤1,q:xa(a 为实数).若 q的一个充分不必要条件是 p,则实数 a 的取值范围是
________.
13. 各棱长均为1且底面为正方形的平行六面体ABCD−ABC D ,满足∠AAB=∠AAD=60°,则
1 1 1 1 1 1
AC =______;此平行六面体的体积为______.
1
14. 已知定义在R上的增函数 f(x)满足对任意的x,x ∈R都有 f(x +x )= f(x )f(x ),且
1 2 1 2 1 2
f(3)=8,函数g(x)满足g(x)+g(4−x)=4,g(6−x)= g(x),且当x∈[ 2,3 ] 时g(x)= f(x−1).若
g(x)在 [ 0,100 ] 上取得最大值的x值依次为x,x,…,x ,取得最小值的x值依次为x′,x′,…,
1 2 k 1 2
k n
x′,则∑
x +g ( x )
+∑
x′+g ( x′)
=______.
n i i i i
i=1 i=1
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
a
15. 已知函数 f ( x )=lnx+ x2 −( a+1 ) x,g ( x ) = −ax2 +( a+1 ) x.
2
( )
(1)讨论函数 f x 的单调性;
(2)若 f
(
x
)+g (
x
)≤0恒成立,求a的取值范围.
16. 有两个盒子,其中1号盒子中有3个红球,2个白球;2号盒子中有6个红球,4个白球.现按照如下
规则摸球.从两个盒子中任意选择一个盒子,再从盒中随机摸出2个球,摸球的结果是一红一白.
(1)你认为较大可能选择的是哪个盒子?请做出你的判断,并说明理由;
(2)如果你根据(1)中的判断,面对相同的情境,作出了5次同样的判断,记判断正确的次数为X,求
X的数学期望(实际选择的盒子与你认为较大可能选择的盒子相同时,即为判断正确).
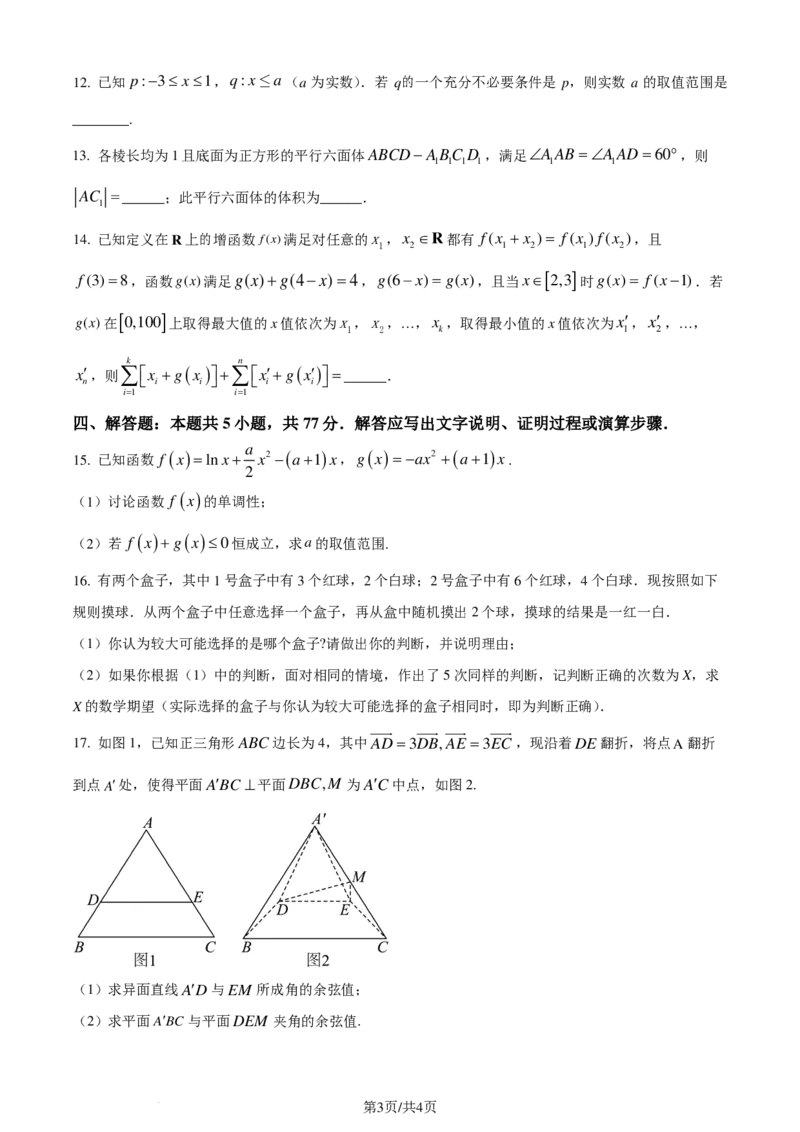
17. 如图1,已知正三角形ABC边长为4,其中AD=3DB,AE =3EC,现沿着DE翻折,将点A翻折
到点A′处,使得平面A′BC ⊥平面DBC,M 为A′C中点,如图2.
(1)求异面直线A′D与EM 所成角的余弦值;
(2)求平面A′BC与平面DEM 夹角的余弦值.
第3页/共4页
学科网(北京)股份有限公司
4
18. 在平面直角坐标系xOy中,已知抛物线C:y2 =2px(p>0)和点R(4,5).点P在C上,且OP = OR.
5
(1)求C的方程;
(2)若过点R作两条直线l 与l ,l 与C相交于A,B两点,l 与C相交于E,D两点,线段AB和
1 2 1 2
ED中点的连线的斜率为k,直线AB,ED,AD,BE 的斜率分别为k ,k ,k ,k ,证明:
1 2 3 4
1 1 1 1 1 1 1
+ = + ,且 + − 为定值.
k k k k k k k
1 2 3 4 3 4
19. 若存在x ∈D使得 f ( x )≤ f ( x ) 对任意x∈D恒成立,则称x 为函数 f ( x ) 在D上的最大值点,记函
0 0 0
( )
数 f x 在D上的所有最大值点所构成的集合为M
(1)若 f ( x )=−x2 +2x+1,D=R,求集合M ;
( )
2x −x x
(2)若 f ( x )= ,D=R ,求集合M ;
4x
(3)设a为大于1的常数,若 f
(
x
)= x+asinx,D=[
0,b
]
,证明,若集合M 中有且仅有两个元素,则
所有满足条件的b从小到大排列构成一个等差数列.
第4页/共4页
学科网(北京)股份有限公司