文档内容
绝密 启用前
★
2023—2024 学年高中毕业班阶段性测试(六)
数学
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码贴在答题
卡上的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需动,用橡
皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.在本试卷上无效
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知集合A={x∣−1< x<4},B= { x∣y =ln ( x−3 )} ,则A∩B=( )
A.{x∣3< x<4} B.{x∣−1< x<4} C.{x∣−3< x<1} D.{x∣x>−1}
3+4i
2.已知i是虚数单位,则 =( )
2+i
A.1 B.2 C. 5 D. 6
6
1
3.3x−
的展开式中x2的系数为( )
x
A.-225 B.60 C.750 D.1215
4.设n为偶数,样本数据x ,x ,,x ( x < x << x ) 的中位数为m,则样本数据
1 2 n 1 2 n
x +x ,x +x ,x +x ,,x +x 的中位数为( )
1 2 2 3 3 4 n−1 n
A.m−1 B.m C.2m−1 D.2m
5.直线l: y =3x+a与曲线y =sin3x相切的一个充分不必要条件为( )
A.a=1 B.a=−2π
4π
C.a=π D.a =
3
1
6.已知cosθ−sinθ= ,则cos4θ=( )
4
学科网(北京)股份有限公司97 15 97 95
A.− B.− C.− D.−
128 16 256 256
3m
7.已知正数m,n满足 +1=2m,若m+2n λmn2恒成立,则实数λ的最小值为( )
n
1 2 1 4
A. B. C. D.
4 5 2 5
8.圆锥甲、乙、丙的母线与底面所成的角相等,设甲、乙、丙的体积分别为V,V ,V ,侧面积分别为S ,S ,S ,
1 2 3 1 2 3
S
高分别为h,h ,h ,若V =V +V ,S =S + 3 ,则h =( )
1 2 3 1 2 3 1 2 2 3
2hh 2hh
A.2 ( h +h )− 1 2 B.2 ( h −h )+ 1 2
1 2 h +h 1 2 h −h
1 2 1 2
h +h hh h −h hh
1 2 − 1 2 1 2 + 1 2
C. D.
2 2 ( h +h ) 2 2 ( h −h )
1 2 1 2
二、多项选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求,全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.在正方体ABCD−ABC D 中,M,N 分别为棱AB,AD的中点,则( )
1 1 1 1 1 1
A.AC ⊥ DC B.A,C ,M,N 四点共面
1 1 1
C.AC ∥平面NDC D.MN ⊥平面NDC
1 1 1
sinx+cosx
10.已知函数 f ( x )= ,则( )
sinxcosx
A. f ( x ) 的定义域为 { x∣x≠kπ,k∈Z }
3π
( )
B. f x 的图象关于点 ,1对称
4
3π
C. f ( x ) 的图象关于直线x=− 对称
4
π
( )
D. f x 在区间0, 上的最小值为2 2
2
11.已知A是抛物线E: y2 =2px(p >0)上的动点,点B (−1,4 ) ,C (−4,0 ) ,O为坐标原点,点A到E的准线
学科网(北京)股份有限公司的距离最小值为1,则( )
A. p =2
5
B. AB 的最小值为
2
1 11
C.tan∠ACB的取值范围是
,
2 2
D.∠ACB ∠ACO
三、填空题:本题共 3小题,每小题 5分,共 15分.
12.已知等比数列 { a } 的各项均为正数,且a +a =17,a +a =68,则a =__________.
n 1 5 3 7 n
MP
13.已知M,N 分别为平行四边形ABCD的边BC,CD的中点,若点P满足6AP+5DA=4DC,则 =
MN
__________.
x2 y2
14.已知双曲线C: − =1(a >0,b>0)的右焦点为F ,左、右顶点分别为A,A ,点M 在C上运动(与
a2 b2 1 2
5
A,A 枃不重合),直线MA 交直线x= a于点N ,若FN⋅MA =0恒成立,则C的离心率为
1 2 2 4 1
__________.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
将一枚质地均匀的正四面体玩具(四个面分别标有数字1,2,3,4)抛掷3次,记录每次朝下的面上的数字.
(1)求3次记录的数字经适当排序后可成等差数列的概率;
( )
(2)记3次记录的最大的数字为X ,求X 的分布列及数学期望E X .
16.(15分)
1
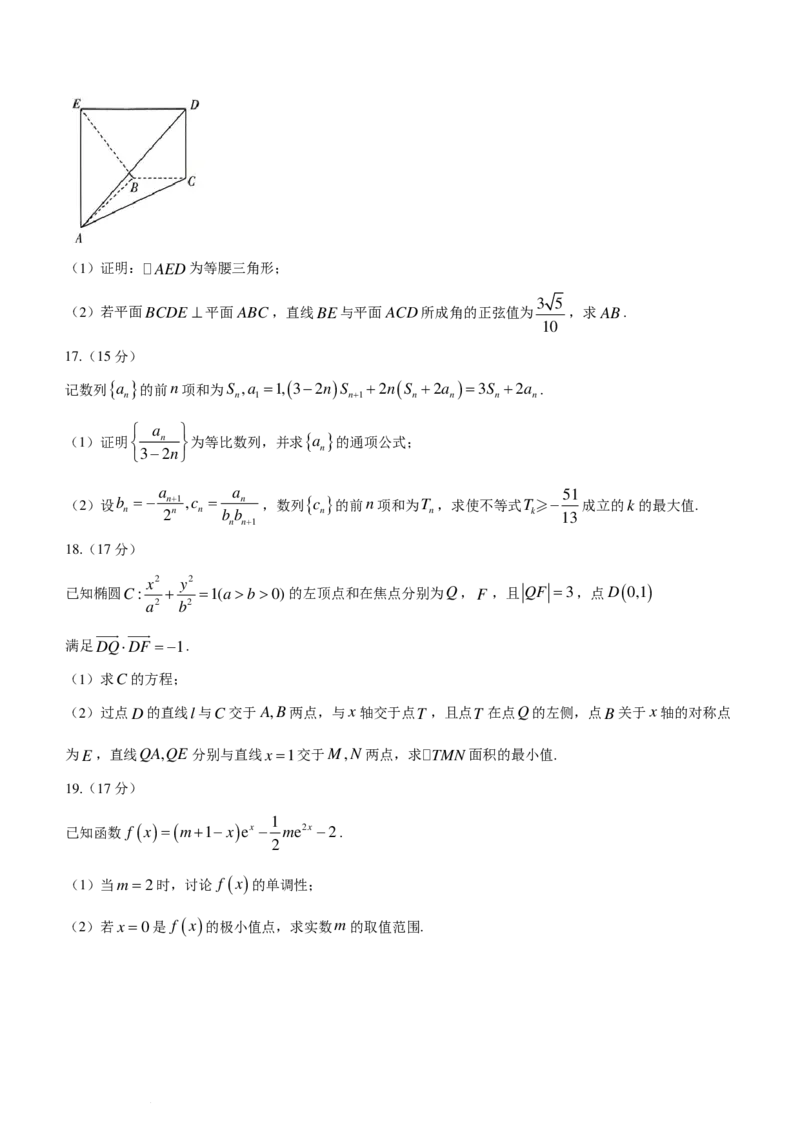
如图,在四棱锥A−BCDE中,AB⊥ BC,BC∥ DE,DC ⊥ BC,BC =CD= DE =1.
2
学科网(北京)股份有限公司(1)证明:AED为等腰三角形;
3 5
(2)若平面BCDE ⊥平面ABC,直线BE与平面ACD所成角的正弦值为 ,求AB.
10
17.(15分)
记数列 { a } 的前n项和为S ,a =1, ( 3−2n ) S +2n ( S +2a )=3S +2a .
n n 1 n+1 n n n n
a
(1)证明 n 为等比数列,并求 { a } 的通项公式;
3−2n n
a a 51
(2)设b
n
=−
2
n
n
+1,c
n
=
b b
n ,数列 { c
n
} 的前n项和为T
n
,求使不等式T
k
−
13
成立的k的最大值.
n n+1
18.(17分)
已知椭圆C:
x2
+
y2
=1(a >b>0)的左顶点和在焦点分别为Q,F ,且 QF =3,点D ( 0,1 )
a2 b2
满足DQ⋅DF =−1.
(1)求C的方程;
(2)过点D的直线l与C交于A,B两点,与x轴交于点T ,且点T 在点Q的左侧,点B关于x轴的对称点
为E,直线QA,QE分别与直线x=1交于M,N 两点,求TMN面积的最小值.
19.(17分)
1
已知函数 f ( x )=( m+1−x ) ex − me2x −2.
2
( )
(1)当m=2时,讨论 f x 的单调性;
(2)若x=0是 f ( x ) 的极小值点,求实数m的取值范围.
学科网(北京)股份有限公司2023—2024 学年高中毕业班阶段性测试(六)
数学·答案
一、单项选择题:本题共 8小题,每小题 5分,共 40分
1.A 2.C 3.D 4.D 5.B 6.A 7.D 8.C
二、多项选择题:本题共 3小题,每小题 6分,共 18分.每小题全部选对的得 6分,部分选对的
得部分分,有选错的得 0分.
9.AC 10.CD 11.ACD
三、填空题:本题共 3小题,每小题 5分,共 15分
2
12.2n−1 13. 14.2
3
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.解析(1)抛掷正四面体玩具3次,所有可能的结果有43 =64种,
3次记录的数字可以排成等差数列,如果3个数字相同,则不同的结果有4种,如果3个数字互不相同,则
不同的结果有2A3 =12种,
3
学科网(北京)股份有限公司4+12 1
因此所求的概率为 = .
64 4
(2)X 的所有可能取值为1,2,3,4,
1
P ( X =1 )= ,
64
C1 +C2 +C3 7
P ( X =2 )= 3 3 3 = ,
64 64
22C1 +2C2 +C3 19
P ( X =3 )= 3 3 3 = ,
64 64
32C1 +3C2 +C3 37
P ( X =4 )= 3 3 3 = .
64 64
故X 的分布列为
X 1 2 3 4
1 7 19 37
P
64 64 64 64
1 7 19 37 55
X 的数学期望E ( X )=1× +2× +3× +4× = .
64 64 64 64 16
16.解析(1)取DE的中点M ,连接BM,AM .
1
因为BC∥ DE,BC = DE = DM ,所以四边形BCDM 是平行四边形,
2
所以BM ∥CD.
因为BC ⊥CD,所以BC ⊥ BM .
又因为AB⊥ BC,AB∩BM = B,所以BC ⊥平面ABM ,
所以DE ⊥平面ABM ,所以DE ⊥ AM ,
即AM 是DE的垂直平分线,所以AE = AD,即AED是等腰三角形.
(2)由(1)知BC ⊥ BM ,因为平面ABC ⊥平面BCDE,所以BM ⊥平面ABC,从而可知
BM,BC,BA两两垂直.
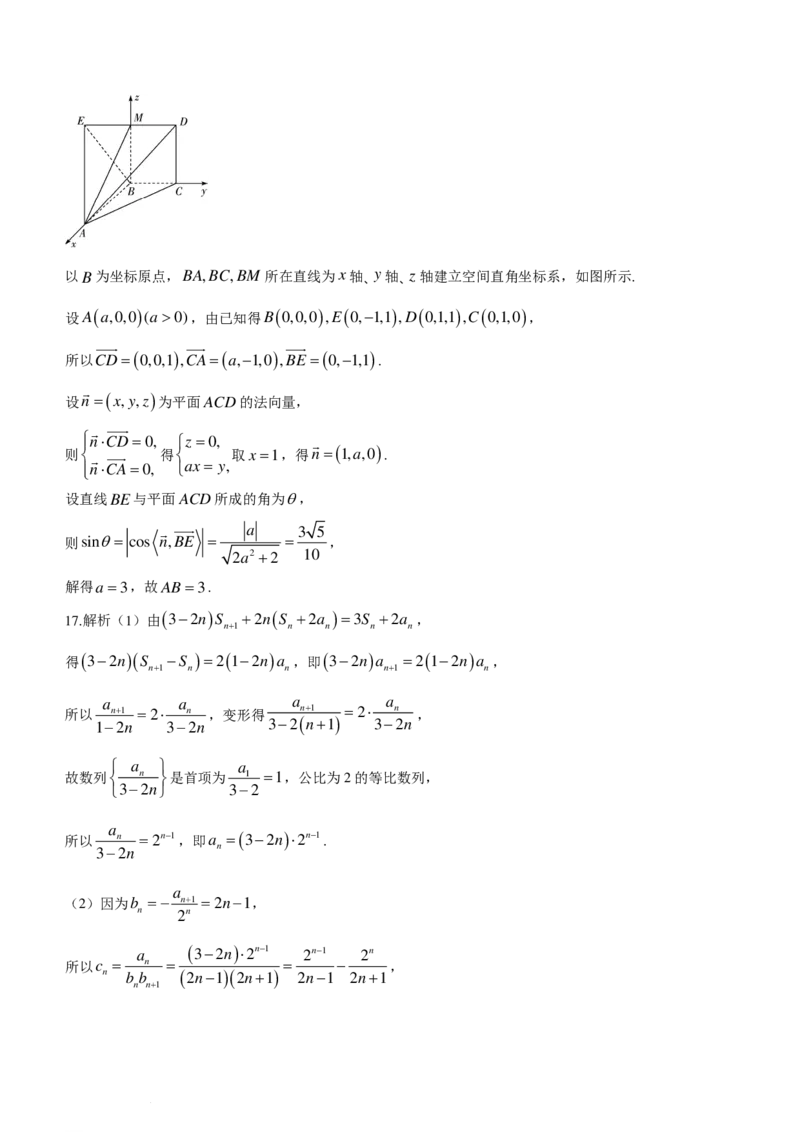
学科网(北京)股份有限公司以B为坐标原点,BA,BC,BM 所在直线为x轴、 y轴、z轴建立空间直角坐标系,如图所示.
设A ( a,0,0 ) (a>0),由已知得B ( 0,0,0 ) ,E ( 0,−1,1 ) ,D ( 0,1,1 ) ,C ( 0,1,0 ) ,
所以CD=( 0,0,1 ) ,CA=( a,−1,0 ) ,BE =( 0,−1,1 ) .
设n
=(
x,y,z
)
为平面ACD的法向量,
n⋅CD=0, z =0,
则 得 取x=1,得n =( 1,a,0 ) .
n⋅CA=0, ax= y,
设直线BE与平面ACD所成的角为θ,
a 3 5
则sinθ= cos n,BE = = ,
2a2 +2 10
解得a=3,故AB=3.
17.解析(1)由 ( 3−2n ) S +2n ( S +2a )=3S +2a ,
n+1 n n n n
得 ( 3−2n )( S −S )=2 ( 1−2n ) a ,即 ( 3−2n ) a =2 ( 1−2n ) a ,
n+1 n n n+1 n
a a a a
所以 n+1 =2⋅ n ,变形得 n+1 =2⋅ n ,
1−2n 3−2n 3−2 ( n+1 ) 3−2n
a a
故数列 n 是首项为 1 =1,公比为2的等比数列,
3−2n 3−2
a
所以 n =2n−1,即a =( 3−2n )⋅2n−1 .
3−2n n
a
(2)因为b =− n+1 =2n−1,
n 2n
a ( 3−2n )⋅2n−1 2n−1 2n
所以c = n = = − ,
n b b ( 2n−1 )( 2n+1 ) 2n−1 2n+1
n n+1
学科网(北京)股份有限公司20 21 21 22 2n−2 2n−1 2n−1 2n 2n
T = − + − ++ − + − =1− .
n 1 3 3 5 2n−3 2n−1 2n−1 2n+1 2n+1
51 2k 51 64 2k
因为T k − 13 ,所以1− 2k+1 − 13 ,即 13 2k+1 .
2n
设函数 f ( n )= ,n∈N*.
2n+1
2n+1 2n ( 4n+2−2n−3 ) 2n ( 2n−1 ) 2n
因为 f ( n+1 )− f ( n )= − = = >0,
2n+3 2n+1 ( 2n+3 )( 2n+1 ) ( 2n+3 )( 2n+1 )
所以 f ( n )=
2n
( n∈N* ) 单调递增.
2n+1
26 64
又 f ( 6 )= = ,所以k6,
2×6+1 13
51
所以使T − 成立的最大正整数k的值为6.
k 13
18.解析(1)由题意知Q (−a,0 ) ,设F ( c,0 ) (c>0).
因为 QF =3,所以a+c=3①.
因为DQ=(−a,−1 ) ,DF =( c,−1 ) ,DQ⋅DF =−1,
所以−ac+1=−1,即ac=2②.
由①②解得a=2,c=1,b= 4−1= 3,
x2 y2
所以C的方程为 + =1.
4 3
(2)设A ( x ,y ) ,B ( x ,y ) ,由题可设直线AB: y =kx+1,则E ( x ,−y ) ,y >0,y >0.
1 1 2 2 2 2 1 2
1 1 1
令 y =0,得x=− ,由− <−2,得00,即 f′(
x
)>0,当x>0时,h (
x
)<0,即 f′(
x
)<0,
所以 f
(
x
)
在
(−∞,0 )
上单调递增,在
( 0,+∞)
上单调递减.
(2)由题意知 f′( x )=( m+1−x−1 ) ex −me2x = ( m−x−mex ) ex,且 f′( 0 )=0.
令函数g
(
x
)=m−x−mex,则g′(
x
)=−1−mex
.
①若m0,则g′(
x
)<0,g (
x
)
在R上单调递减.
又g
(
0
)=0,则当x<0时,g (
x
)>0,所以 f′(
x
)>0,
f
(
x
)
在
(−∞,0 )
上单调递增,
当x>0时,g
(
x
)<0,所以 f′(
x
)<0,
f
(
x
)
在
( 0,+∞)
上单调递减.
( )
所以 f x 在x=0处取得极大值,不合题意.
1 1 1
②若−10,令g′( x )<0,得x0,从而 f′(
x
)>0,
f
(
x
)
在
(−∞,0 )
上单调递增;
1 1
当0< x0,解得x>0,令g′( x )<0,解得x<0,
m
所以g
(
x
)
在
(−∞,0 )
上单调递减,在
( 0,+∞)
上单调递增,
所以g
(
x
)
在x=0处取得极小值,也是最小值,所以g
(
x
)
g
(
0
)=0,从而 f′(
x
)
0,
所以 f
(
x
)
在
(−∞,+∞)
上单调递增,不合题意.
学科网(北京)股份有限公司 1
④若m<−1,则ln − <0,
m
1 1
令g′( x )>0,解得x>ln − ,故g ( x ) 在ln − ,+∞ 上单调递增.
m m
1
又 ( 0,+∞)⊆ ln − ,+∞ ,g ( 0 )=0,
m
1 1
故当ln − < x<0时,g ( x )<0,从而 f′( x )<0, f ( x ) 在ln − ,0上单调递减,
m m
当x>0时,g
(
x
)>0,从而 f′(
x
)>0,
f
(
x
)
在
( 0,+∞)
上单调递增.
( )
所以 f x 在x=0处取得极小值,符合题意.
综上,m的取值范围是 (−∞,−1 ) .
学科网(北京)股份有限公司