文档内容
绝密★启用前
2024 年普通高等学校招生全国统一考试模拟试题(一)
数学
本试卷共4页,19题.全卷满分150分.考试用时120分钟.
★祝考试顺利★
注意事项:
1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考证
号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在
试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和
答题卡上的非答题区域均无效.
4.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.设 为虚数单位,若复数 满足 ,则|| ( )
A.1 B. C. D.2
2.已知集合 ,集合 ,则集合 与集合 的关系为( )
A. B. C. D.
3.一个容量为10的样本,6,7,8,9,10,13,14,15,17,18,则该组数据的上四分位数为( )
A.8 B.7.5 C.14.5 D.15
4.已知直线 与 交于 两点, ,则 ( )
A.1 B. C. D.
5.考虑以 为样本空间的古典概型.设 和 定义在 上,取值于 的成对分类变量,则“
与 独立”是“ 与 独立”的( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条
件
学科网(北京)股份有限公司6. ,则 的最小值为( )
A. B. C. D.6
7.已知数列 通项公式为 ,将数列 的公共项从小到大排列得到数列
,设数列 的阅 项和为 ,则 ( )
A. B. C. D.
8.一个半径为1的小球在一个内壁棱长为 的正四面体封闭容器内可向各个方向自由运动,则该小球表
面永远不可能接触到的容器内壁的面积是( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.四个实数 按照一定的顺应构成一个等比数列,则 的可能取值有( )
A. B. C.128 D.
10.已知函数 且满足 ,对任意的
恒有 ,且 为 的极值点,则下列等式成立的是( )
A. B.
C. D.
11.已知 分别为双曲线 的左、右焦点,过点 的直线与双曲线的右支交于
两点,记 的内切圆 的半径为 的内切圆 的半径为 .若双曲线的离心率 ,
则下列说法正确的是( )
A.双曲线的渐近线方程: B.以 为直径的圆与直线 相切
学科网(北京)股份有限公司C. 内切圆半径最小值是 D. 的范围是
三、填空题:本题共3小题,每小题5分,共15分.
12.函数 的对称中心为_________.
13.抛物线 的焦点为 ,直线 过 分别交抛物线 于点 ,且直线 父
轴于 ,其中 ,则 点坐标为_________.
14.对于任意的实数 ,函数 在 上至少3个零点,至多4个零点,
则 的取值范围为_________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)
发展新能源汽车是我国从汽车大国迈向汽车强国的必由之路,是应对气候变化推动绿色发展的战路举措.随
着国务院《新能源汽车产业发展规划(2021—2035)》的发布,我国自主品牌汽车越来越具备竞争力,国产
某品牌汽车对市场进行调研,统计了该品牌新能源汽车在某城市2023年前几个月的销售量(单位:辆),用
y表示第x月份该市汽车的销售量,得到如下统计表格:
1 2 3 4 5 6 7
2
32 37 45 47 52 60
8
(1)经研究, 满足线性相关关系,求 关于 的线性回归方程 ( 按四舍五入精确到
整数);
(2)该市某 店为感谢客户,决定针对该品牌的汽车成交客户开展抽奖活动,设“一等奖”、“二等奖”
和“祝您平安”三种奖项,“一等奖”奖励5千元;“二等奖”奖励3千元;“祝您平安”奖励纪念品一份.
在一次抽奖活动中获得“二等奖”的概率为 ,获得一份纪念品的概率为 ,现有甲、乙两个客户参与抽
奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额 (千元)的分布列及数学期望.
参考数据及公式: .
16.(本小题满分15分)
学科网(北京)股份有限公司在 中,角 的对边分别为 ,若 .
(1)求角 的大小;
(2)若 为 上一点,且 为 的角平分线, ,求 的最大值.
17.(本小题满分15分)
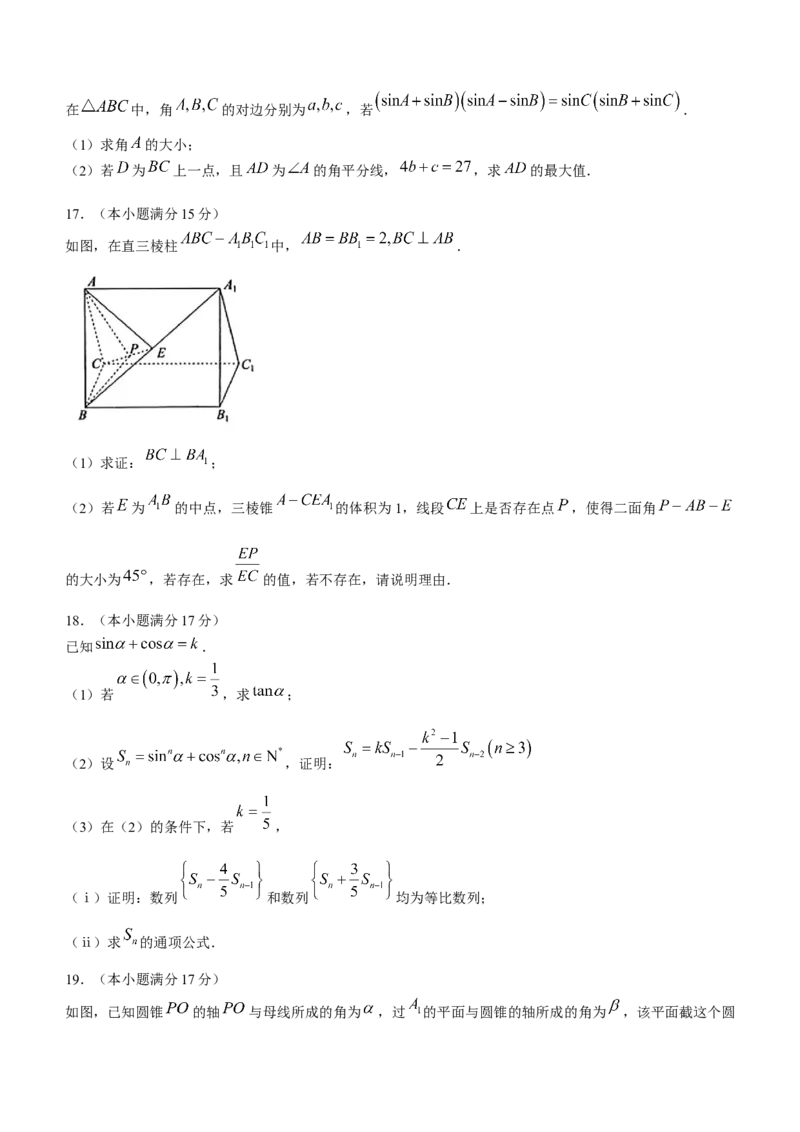
如图,在直三棱柱 中, .
(1)求证: ;
(2)若 为 的中点,三棱锥 的体积为1,线段 上是否存在点 ,使得二面角
的大小为 ,若存在,求 的值,若不存在,请说明理由.
18.(本小题满分17分)
已知 .
(1)若 ,求 ;
(2)设 ,证明:
(3)在(2)的条件下,若 ,
(ⅰ)证明:数列 和数列 均为等比数列;
(ⅱ)求 的通项公式.
19.(本小题满分17分)
如图,已知圆锥 的轴 与母线所成的角为 ,过 的平面与圆锥的轴所成的角为 ,该平面截这个圆
学科网(北京)股份有限公司锥所得的截面为椭圆 ,椭圆 的长轴为 ,短轴为 ,长半轴长为 的中心为 ,再以 为
弦且垂直于 的圆截面,记该圆与直线 交于 ,与直线 交于 ,设 .
(1)求椭圆 的焦距;
(2)椭圆 左右焦点分别为 上不同两点 ,满足 ,设直线 交于点
,求四边形 的面积.
学科网(北京)股份有限公司