湖南省长沙市长郡中学2023-2024学年高三下学期二模数学试题Word版含解析(1)(1)_2024年4月_024月合集_2024届湖南省长沙市长郡中学高三下学期二模

长郡中学 2024 届高考适应性考试（二）
数学
命题人：__________审题人__________
注意事项：
1.答卷前，考生务必将自己的姓名､准考证号填写在答题卡上.
2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改
动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本
试卷上无效.
3.考试结束后，将本试卷和答题卡一并交回.
一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的.
1.已知集合A  x∣x2 2x30  ,B  y∣y 2x,x1  ，则AB（ ）
A.
,3
B.
0,2
C.
1,2
D.
2,3
1 1
2.已知数列 a  满足a  ，若a  ，则a （ ）
n n1 1a 1 2 2023
n
1
A.2 B.-2 C.-1 D.
2
3.已知样本数据x ,x ,L ,x 的平均数和标准差均为4，则数据x 1,x 1,L ,x 1的平均数与方
1 2 100 1 2 100
差分别为（ ）
A.5,4 B.5,16 C.4,16 D.4,4
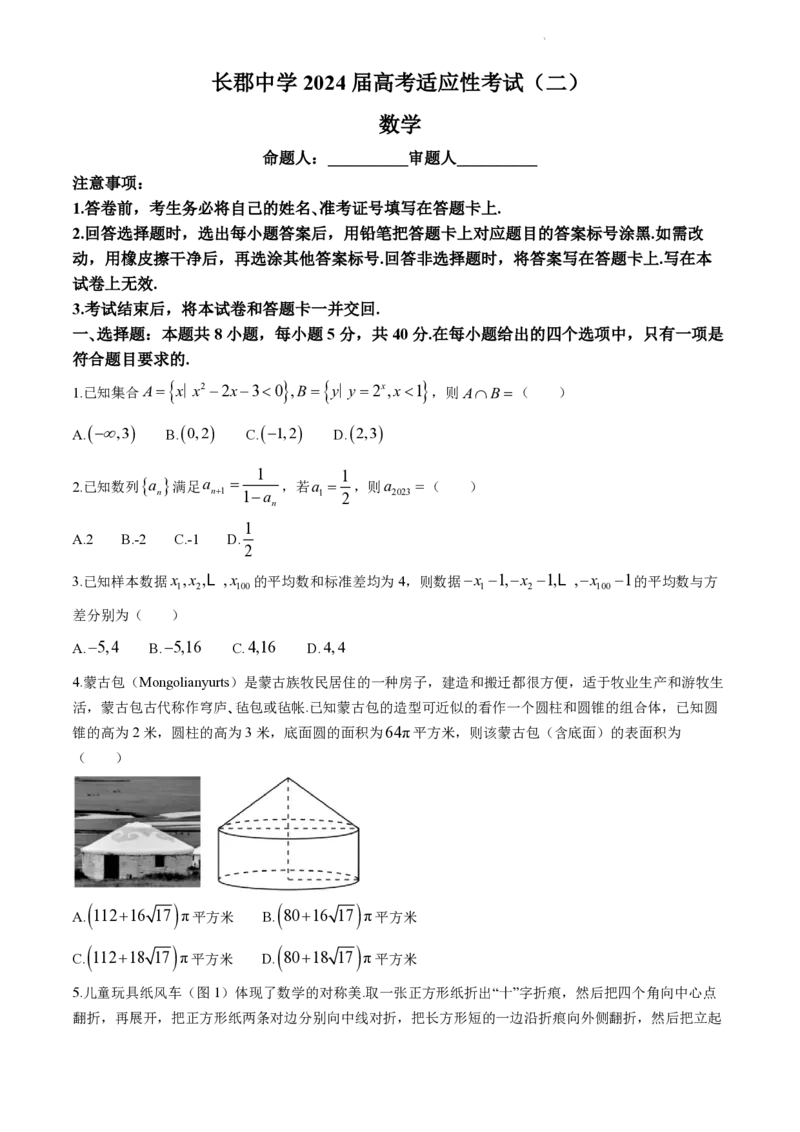
4.蒙古包（Mongolianyurts）是蒙古族牧民居住的一种房子，建造和搬迁都很方便，适于牧业生产和游牧生
活，蒙古包古代称作穹庐､毡包或毡帐.已知蒙古包的造型可近似的看作一个圆柱和圆锥的组合体，已知圆
锥的高为2米，圆柱的高为3米，底面圆的面积为64π平方米，则该蒙古包（含底面）的表面积为
（ ）
   
A. 11216 17 π平方米 B. 8016 17 π平方米
   
C. 11218 17 π平方米 D. 8018 17 π平方米
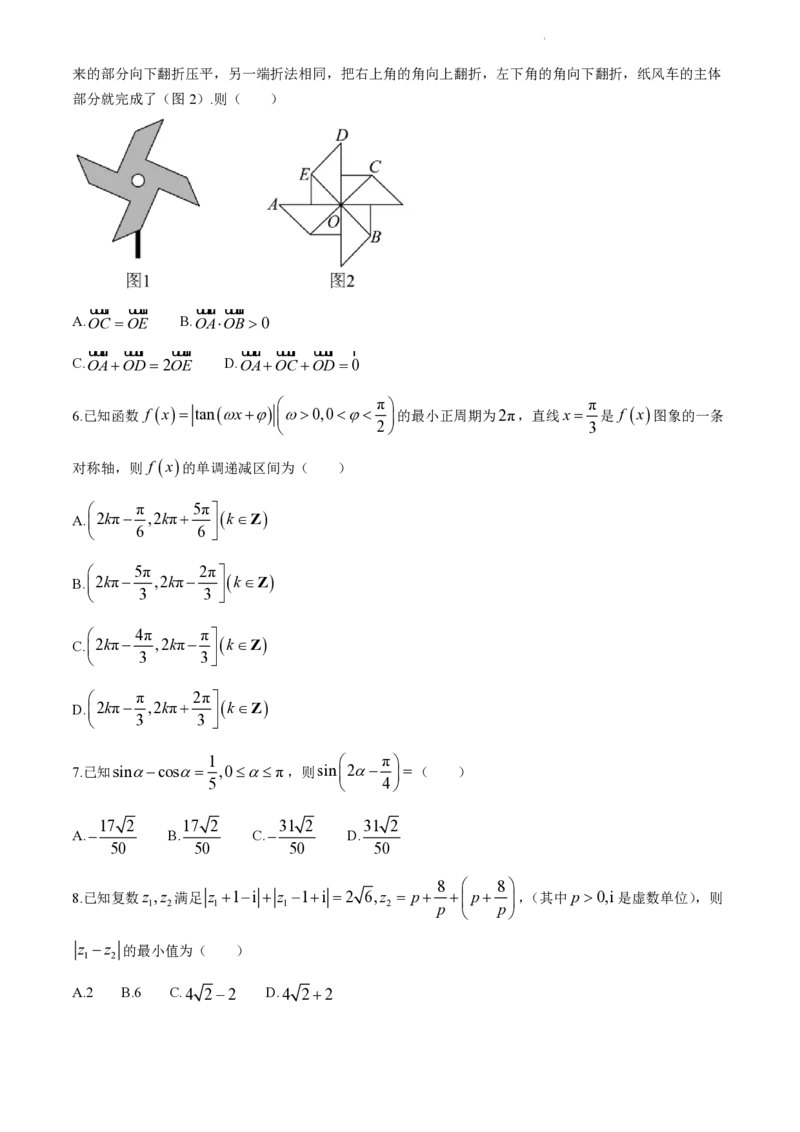
5.儿童玩具纸风车（图1）体现了数学的对称美.取一张正方形纸折出“十”字折痕，然后把四个角向中心点
翻折，再展开，把正方形纸两条对边分别向中线对折，把长方形短的一边沿折痕向外侧翻折，然后把立起
学科网（北京）股份有限公司来的部分向下翻折压平，另一端折法相同，把右上角的角向上翻折，左下角的角向下翻折，纸风车的主体
部分就完成了（图2）.则（ ）
uuur uuur uuur uuur
A.OC OE B.OAOB0
uuur uuur uuur uuur uuur uuur r
C.OAOD2OE D.OAOCOD0
 π π
6.已知函数 f x tanx  0,0 的最小正周期为2π，直线x 是 f x 图象的一条
 2 3
对称轴，则 f x 的单调递减区间为（ ）
 π 5π
A. 2kπ ,2kπ  kZ
 6 6 
 5π 2π
B. 2kπ ,2kπ  kZ
 3 3 
 4π π
C. 2kπ ,2kπ  kZ
 3 3
 π 2π
D. 2kπ ,2kπ  kZ
 3 3 
1  π
7.已知sincos ,0π，则sin  2  （ ）
5  4
17 2 17 2 31 2 31 2
A. B. C. D.
50 50 50 50
8  8 
8.已知复数z ,z 满足 z 1i  z 1i 2 6,z  p   p ，（其中 p 0,i是虚数单位），则
1 2 1 1 2 p  p
z z 的最小值为（ ）
1 2
A.2 B.6 C.4 22 D.4 22
学科网（北京）股份有限公司二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目
要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分.
9.下列函数中最小值为2的是（ ）
1
A.y  x2 2x3 B. y  sinx 
sinx
1
C.y 2x 21x D.y lnx
lnx
8
10.若x,y满足(x y)2  xy 2，则（ ）
3
A.yx 3 B.yx2
3 3
C.xy  D.xy
2 4
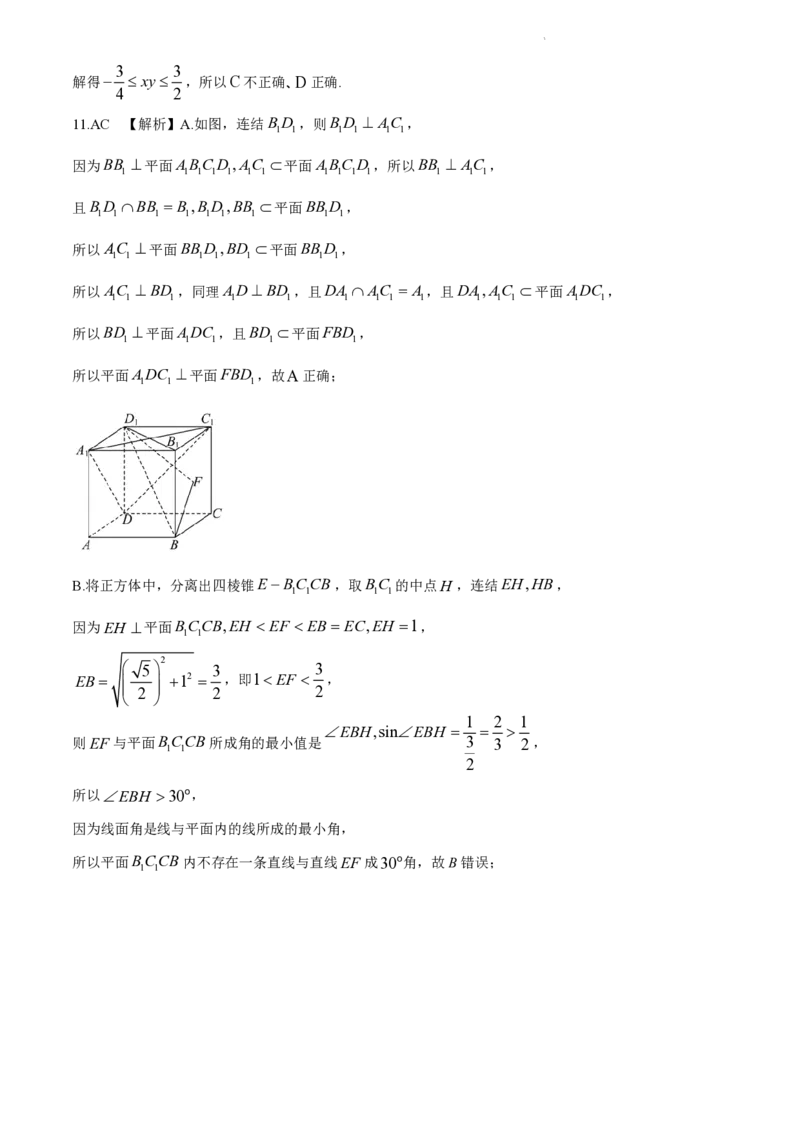
11.在正方体ABCDABC D 中，AB1,E为AD 的中点，F 是正方形BBCC内部一点（不含边
1 1 1 1 1 1 1 1
界），则（ ）
A.平面FBD 平面AC D
1 1 1
B.平面BBCC内存在一条直线与直线EF 成30o角
1 1
C.若F 到BC边距离为d ，且EF2 d2 1，则点F 的轨迹为抛物线的一部分
D.以VAAD 的边AD 所在直线为旋转轴将VAAD 旋转一周，则在旋转过程中，A到平面ABC的距离
1 1 1 1 1 1 1
 3 6 3 6
的取值范围是  ,  
3 5 3 5
 
三､填空题：本题共 3小题，每小题 5分，共 15分.
6
 m
12.已知

x

的展开式中常数项为20，则实数m的值为__________.
 x 
13.已知定义在R上的偶函数 f x 满足 f x  f x  f x x  ，且当x0时， f x0.若
1 2 1 2
 1  1
f 3 f3a，则 f x 在点  , f   处的切线方程为__________.（用含a的表达式表示）
 3  3
y2
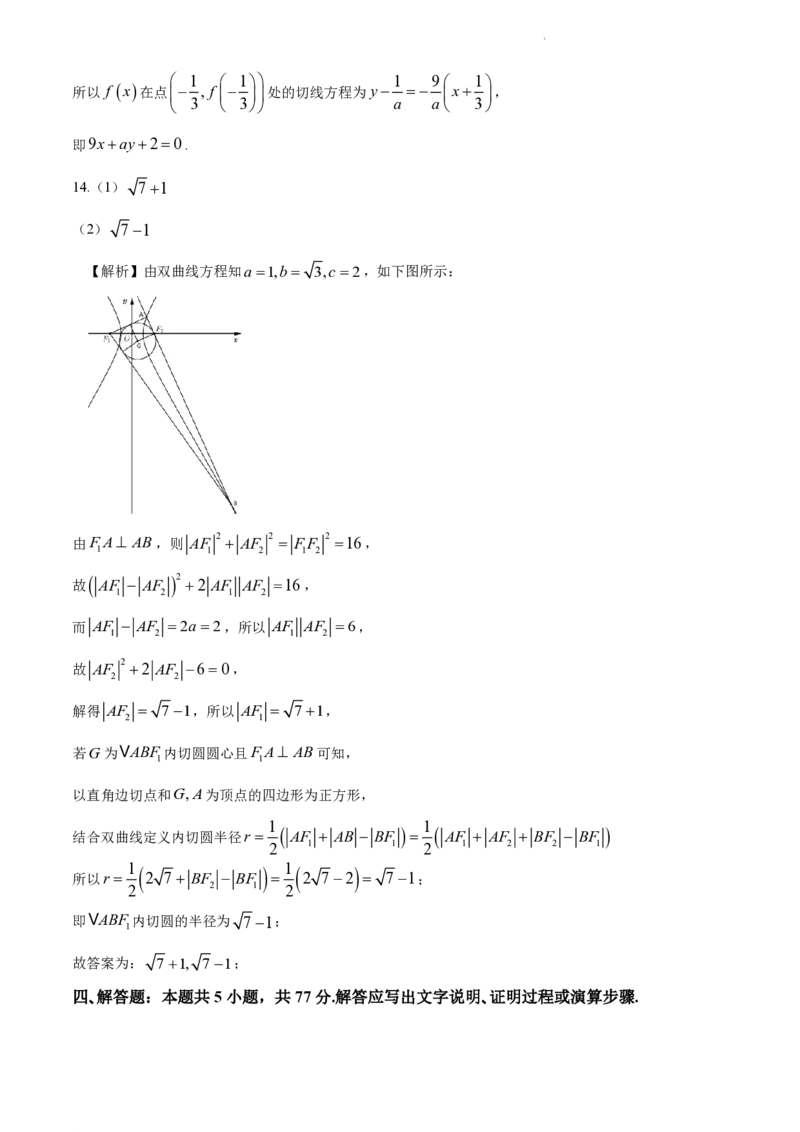
14.已知双曲线C:x2  1的左､右焦点分别为F,F ，右顶点为E，过F 的直线交双曲线C的右支于
1 2 2
3
A,B两点（其中点A在第一象限内），设M,N 分别为VAFF ,VBFF 的内心，则当FA AB时，
1 2 1 2 1
AF __________；VABF内切圆的半径为__________.
1 1
四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤.
学科网（北京）股份有限公司15.（本小题满分13分）
已知在VABC中，内角A,B,C所对的边分别为a,b,c，其中a 4,4 3cosC  3bcsinA.
（1）求A；
2 2
（2）已知直线AM 为BAC的平分线，且与BC交于点M ，若AM  ，求VABC的周长.
3
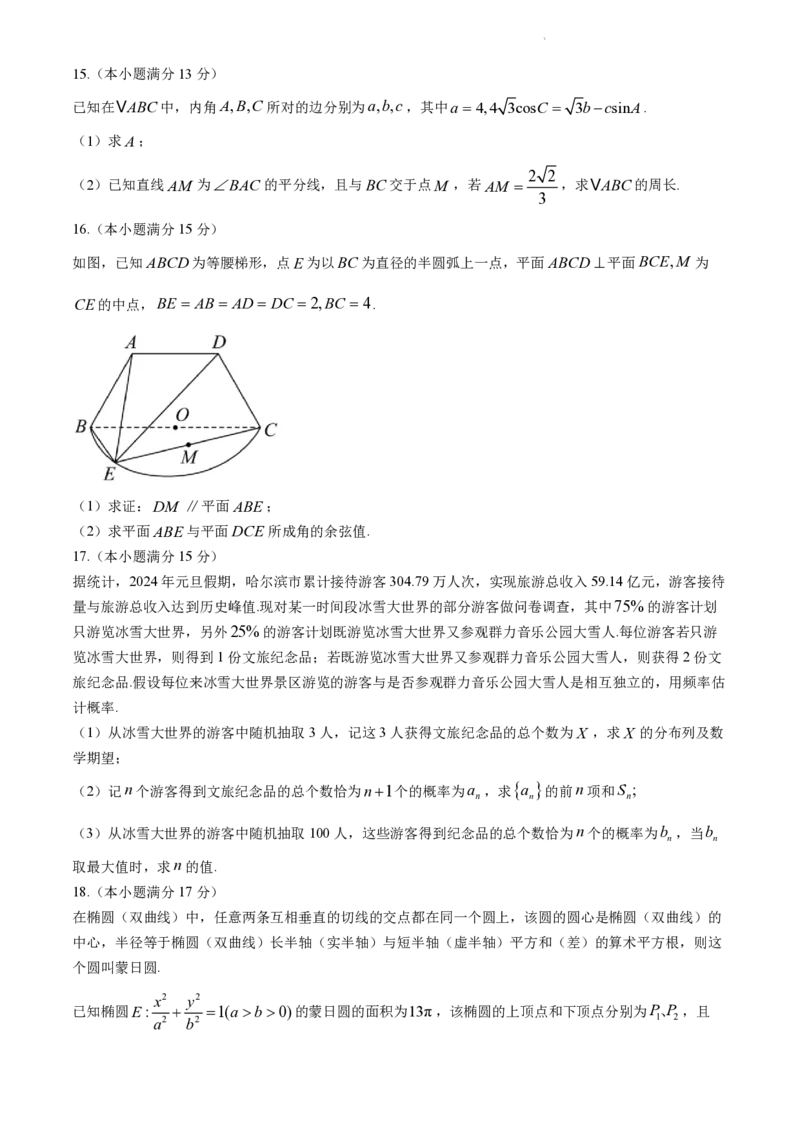
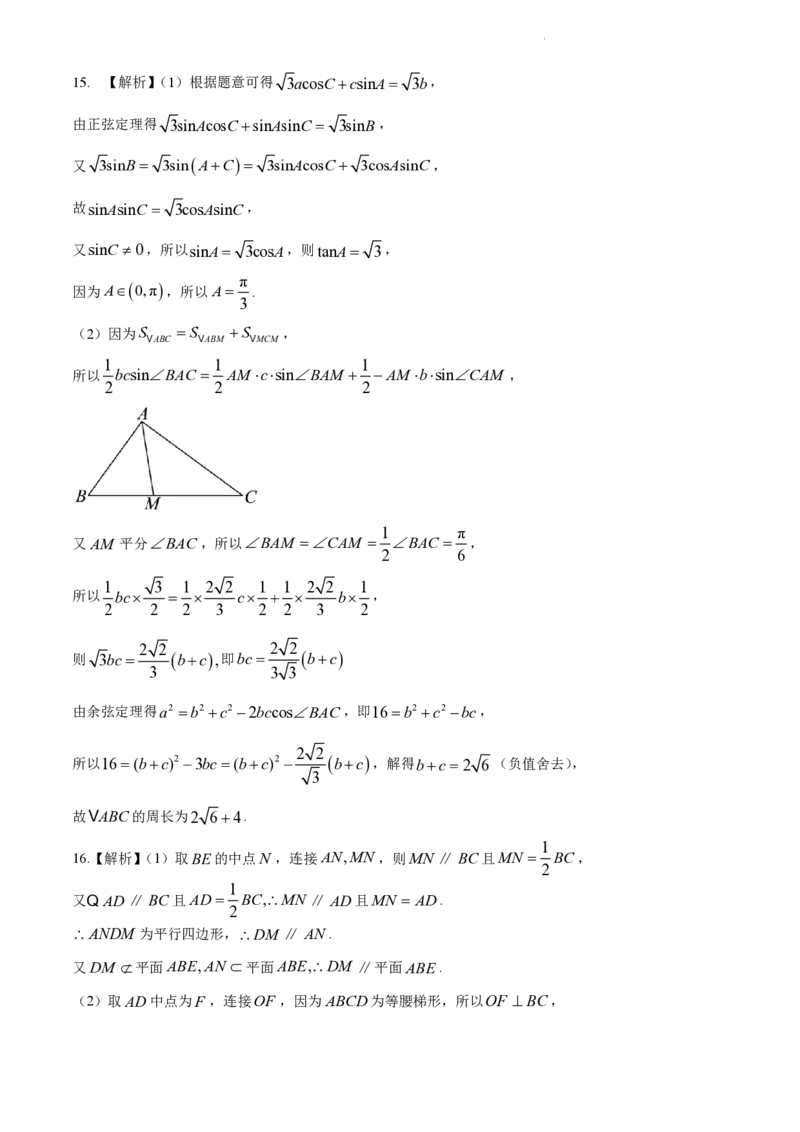
16.（本小题满分15分）
如图，已知ABCD为等腰梯形，点E为以BC为直径的半圆弧上一点，平面ABCD平面BCE,M 为
CE的中点，BE  AB AD DC 2,BC 4.
（1）求证：DM ∥平面ABE；
（2）求平面ABE与平面DCE所成角的余弦值.
17.（本小题满分15分）
据统计，2024年元旦假期，哈尔滨市累计接待游客304.79万人次，实现旅游总收入59.14亿元，游客接待
量与旅游总收入达到历史峰值.现对某一时间段冰雪大世界的部分游客做问卷调查，其中75%的游客计划
只游览冰雪大世界，另外25%的游客计划既游览冰雪大世界又参观群力音乐公园大雪人.每位游客若只游
览冰雪大世界，则得到1份文旅纪念品；若既游览冰雪大世界又参观群力音乐公园大雪人，则获得2份文
旅纪念品.假设每位来冰雪大世界景区游览的游客与是否参观群力音乐公园大雪人是相互独立的，用频率估
计概率.
（1）从冰雪大世界的游客中随机抽取3人，记这3人获得文旅纪念品的总个数为X ，求X 的分布列及数
学期望；
（2）记n个游客得到文旅纪念品的总个数恰为n1个的概率为a ，求 a  的前n项和S ;
n n n
（3）从冰雪大世界的游客中随机抽取100人，这些游客得到纪念品的总个数恰为n个的概率为b ，当b
n n
取最大值时，求n的值.
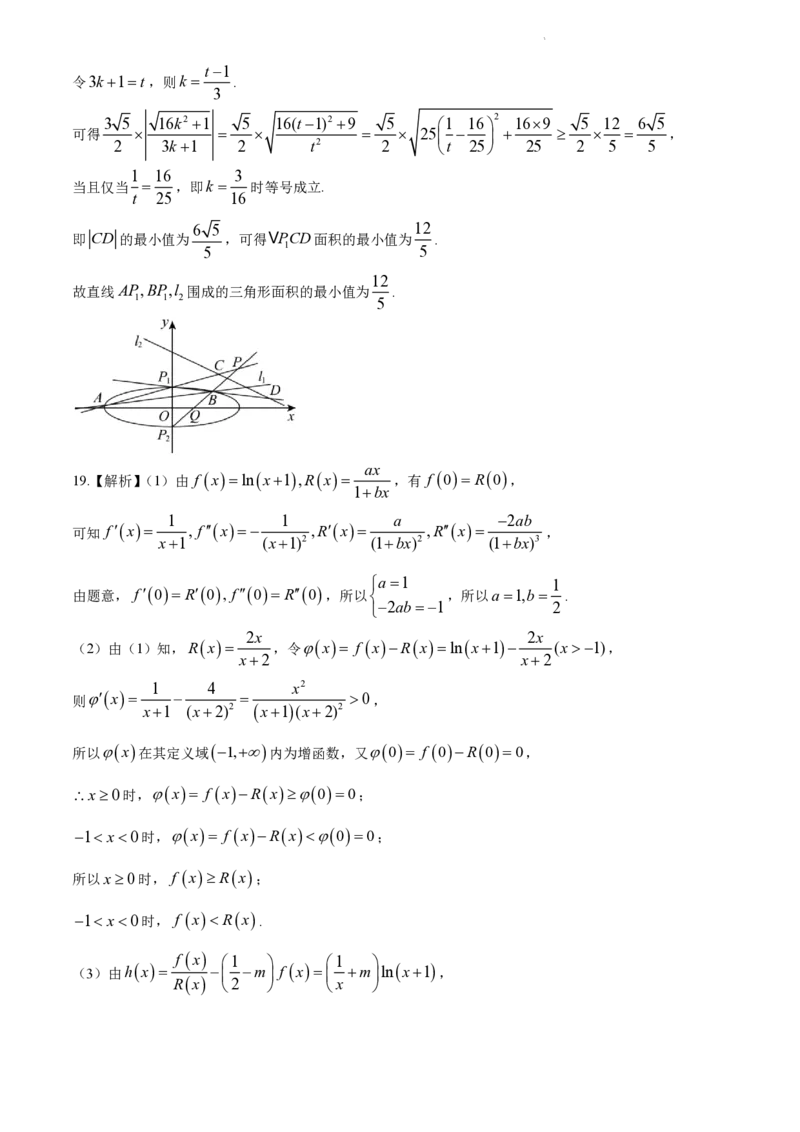
18.（本小题满分17分）
在椭圆（双曲线）中，任意两条互相垂直的切线的交点都在同一个圆上，该圆的圆心是椭圆（双曲线）的
中心，半径等于椭圆（双曲线）长半轴（实半轴）与短半轴（虚半轴）平方和（差）的算术平方根，则这
个圆叫蒙日圆.
x2 y2
已知椭圆E:  1(a b0)的蒙日圆的面积为13π，该椭圆的上顶点和下顶点分别为P､P ，且
a2 b2 1 2
学科网（北京）股份有限公司 1
PP 2，设过点Q

0, 的直线l 与椭圆E交于A,B两点（不与P,P
1 2  2 1 1 2
两点重合）且直线l :x2y60.
2
（1）证明：AP,BP 的交点P在直线y 2上；
1 2
（2）求直线AP,BP,l 围成的三角形面积的最小值.
1 2 2
19.（本小题满分17分）
帕德近似是法国数学家亨利·帕德发明的用有理多项式近似特定函数的方法.给定两个正整数m,n，函数
f x 在x0处的 m,n 阶帕德近似定义为：
a a xL a xm
Rx 0 1 m ，且满足：
1bxL b xn
1 n
f 0 R0, f0 R0, f0 R0,L L , f
 mn 
0 R
 mn 
0.
（注： fxfx ' , fxfx ' , f 4xfx ' , f 5xf 4x ' ,; f nx为
       
f
n1x的导数）
ax
已知 f xlnx1 在x0处的 1,1 阶帕德近似为Rx .
1bx
（1）求实数a,b的值；
（2）比较 f x 与Rx 的大小；
f x 1 
（3）若hx   m  f x 在 0, 上存在极值，求m的取值范围.
Rx 2 
学科网（北京）股份有限公司长郡中学 2024 届高考适应性考试（二）
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B D B A C B D B AB ABD AC
一､选择题：本题共 8小题，每小题 5分，共 40分。
1.B 【解析】由x2 2x30，得 x3x10，解得1 x3，
所以A{x∣1 x3}，
因为x1，
所以以02x 21 2，
所以B{y∣0 y2}，
所以AB{x∣1 x3}{y∣0 y2}0,2 .
1 1
2.D 【解析】因为a  ,a  ，
n1 1a 1 2
n
1 1 1 1
a   2,a   1
所以 2 1a 1 3 1a 12 ，
1 1 2
2
1 1 1
a    ，
4 1a 11 2
3
所以数列
a 
的周期为3.
n
1
所以a a a  .
2023 36741 1 2
uuur uuur uuur uuur uuur
5.C 【解析】不妨设|OB||OC||OE|1，则|OA||OD| 2，
uuur uuur uuur uuur
对于A项，显然OC与OE方向不一致，所以OC OE，故A项错误；
对于B项，由图知AOB是钝角，
uuur uuur uuur uuur
则OAOB|OA||OB|cosAOB0，故B项错误；
对于C项，由题意知点E是线段AD的中点，
uuur 1 uuur uuur  uuur uuur uuur
则易得：OE  OAOD ，即得：OAOD2OE ，故C项正确；
2
uuur uuur uuur uuur uuur uuur uuur uuur
 
对于D项，由OAOCOD OAOD OC 2OEOC，
uuur uuur uuur uuur uuur r
而OE与OC显然不共线，故OAOCOD0.即D项错误.
学科网（北京）股份有限公司1 1
7.D 【解析】将sincos 平方得12sincos ，
5 25
24  π
所以2sincos ，则  0, .
25  2
24 49
所以(sincos)2 12sincos1  ，
25 25
7
从而sincos .
5
 1  4
sincos sin
 
 5  5
联立 ，得 .
7 3
 
sincos cos
 5  5
2 2
24 3 4 7
所以sin22sincos ,cos2cos2sin2       .
25 5 5 25
 π 2 2 24 7  31 2
故sin  2   sin2cos2       .
 4 2 2 25 25 50
8.B 【解析】设z  x yi，（其中xR,yR,i是虚数单位），
1
z 在复平面的对应点Z x,y ，
1 1
则 z 1i  z 1i  x1y1i  x1y1i
1 1
 (x1)2 (y1)2  (x1)2 (y1)2 2 6
即点Z 的轨迹表示为焦点分别在 1,1,1,1 的椭圆，
1
且该椭圆的长轴为直线y x，短轴为直线y  x .长半轴长为a  6，
1
半焦距c (11)2 (11)2  2，短半轴长为b a2 c2 2.
2
因为 p0
8 8
所以 p 2 p 4 2
p p
 8 8 
设z 在复平面的对应点Z

p , p

,(p 0).
2 2  p p
 
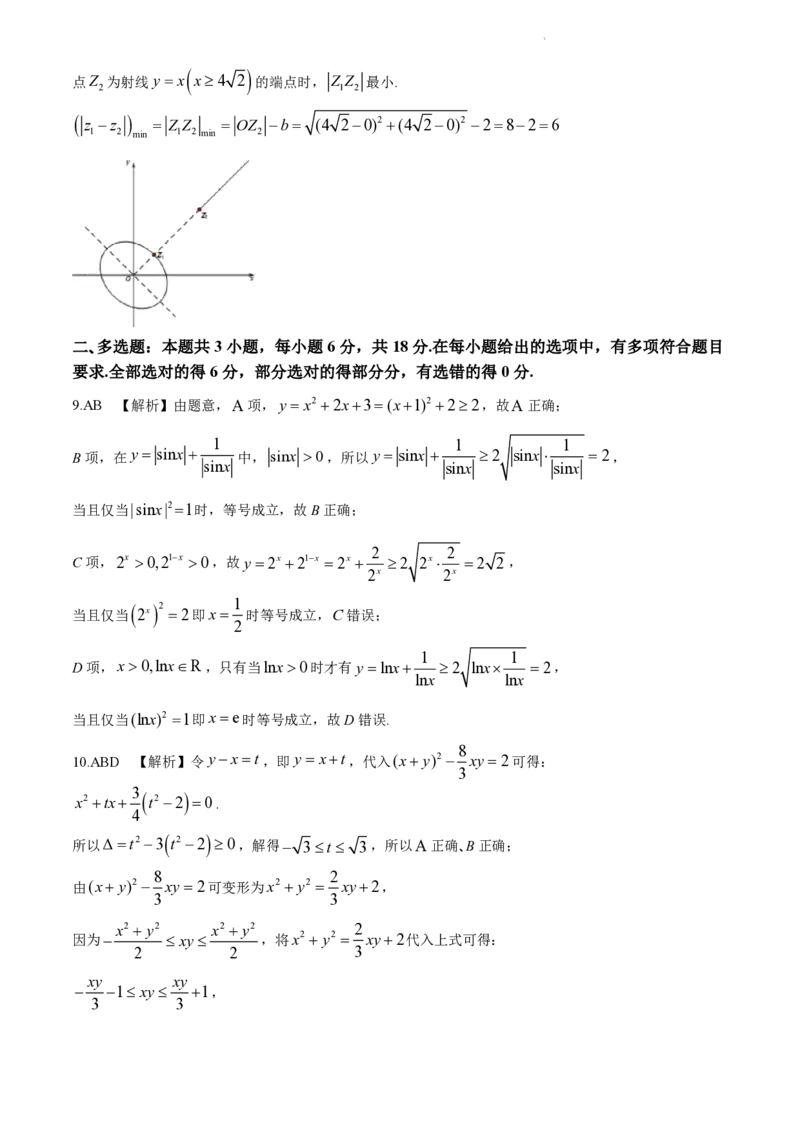
即点Z 的轨迹表示为射线y  x x4 2 上的点.
2
若使得 z z 最小，则需 Z Z 取得最小值，即点Z 为第一象限内的短轴端点，
1 2 1 2 1
学科网（北京）股份有限公司 
点Z 为射线y  x x4 2 的端点时， Z Z 最小.
2 1 2
 z z   Z Z  OZ b (4 20)2 (4 20)2 2826
1 2 min 1 2 min 2
二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目
要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分.
9.AB 【解析】由题意，A项，y  x2 2x3(x1)2 22，故A正确；
1 1 1
B项，在y  sinx  中， sinx 0，所以y  sinx  2 sinx  2，
sinx sinx sinx
当且仅当|sinx|21时，等号成立，故B正确；
2 2
C项，2x 0,21x 0，故y 2x 21x 2x  2 2x 2 2 ，
2x 2x
1
当且仅当
 2x2
2即x 时等号成立，C错误；
2
1 1
D项，x0,lnxR，只有当lnx0时才有y lnx 2 lnx 2，
lnx lnx
当且仅当(lnx)2 1即xe时等号成立，故D错误.
8
10.ABD 【解析】令yxt，即y  xt，代入(x y)2  xy 2可得：
3
3
x2 tx  t2 2  0.
4
所以Δt2 3  t2 2  0，解得 3 t  3，所以A正确､B正确；
8 2
由(x y)2  xy 2可变形为x2  y2  xy2，
3 3
x2  y2 x2  y2 2
因为  xy ，将x2  y2  xy2代入上式可得：
2 2 3
xy xy
 1 xy 1，
3 3
学科网（北京）股份有限公司3 3
解得  xy ，所以C不正确､D正确.
4 2
11.AC 【解析】A.如图，连结BD ，则BD  AC ，
1 1 1 1 1 1
因为BB 平面ABC D,AC 平面ABC D ，所以BB  AC ，
1 1 1 1 1 1 1 1 1 1 1 1 1 1
且BD BB  B,BD,BB 平面BBD ，
1 1 1 1 1 1 1 1 1
所以AC 平面BBD,BD 平面BBD ，
1 1 1 1 1 1 1
所以AC  BD ，同理AD BD ，且DA AC  A，且DA,AC 平面ADC ，
1 1 1 1 1 1 1 1 1 1 1 1 1 1
所以BD 平面ADC ，且BD 平面FBD ，
1 1 1 1 1
所以平面ADC 平面FBD ，故A正确；
1 1 1
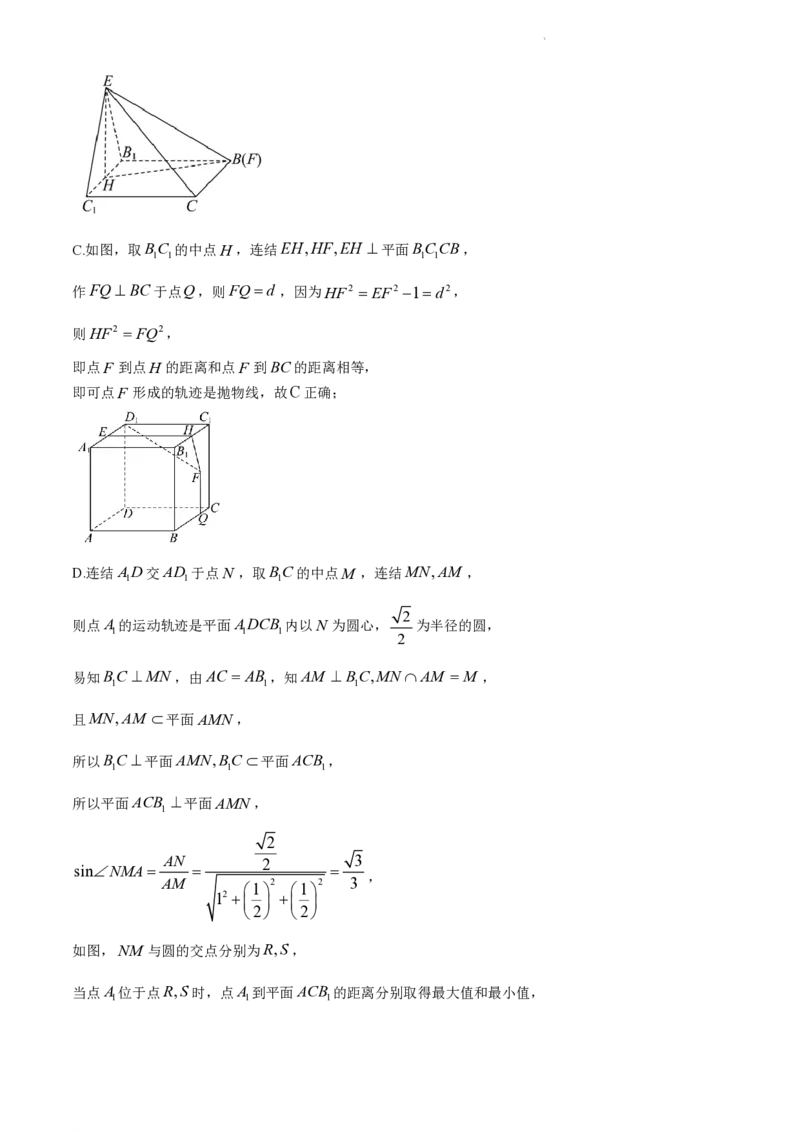
B.将正方体中，分离出四棱锥EBCCB，取BC 的中点H ，连结EH,HB，
1 1 1 1
因为EH 平面BCCB,EH  EF  EB EC,EH 1，
1 1
2
 5 3 3
EB   12  ，即1 EF  ，
 2  2 2
 
1 2 1
EBH,sinEBH   
则EF 与平面BCCB所成角的最小值是 3 3 2 ，
1 1
2
所以EBH 30o，
因为线面角是线与平面内的线所成的最小角，
所以平面BCCB内不存在一条直线与直线EF 成30o角，故B错误；
1 1
学科网（北京）股份有限公司C.如图，取BC 的中点H ，连结EH,HF,EH 平面BCCB，
1 1 1 1
作FQ BC于点Q，则FQd ，因为HF2  EF2 1d2，
则HF2  FQ2，
即点F 到点H 的距离和点F 到BC的距离相等，
即可点F 形成的轨迹是抛物线，故C正确；
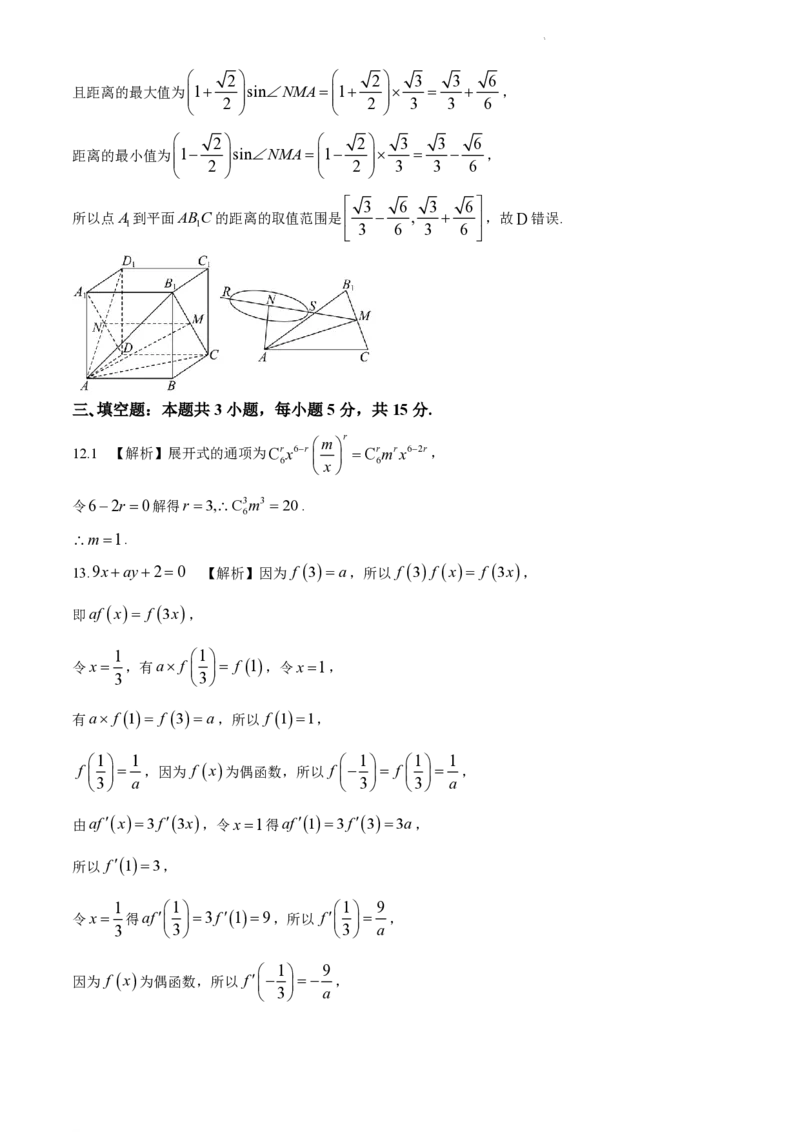
D.连结AD交AD 于点N ，取BC的中点M ，连结MN,AM ，
1 1 1
2
则点A的运动轨迹是平面ADCB 内以N 为圆心， 为半径的圆，
1 1 1
2
易知BC MN ，由AC  AB ，知AM  BC,MN AM M ，
1 1 1
且MN,AM 平面AMN ，
所以BC 平面AMN,BC 平面ACB ，
1 1 1
所以平面ACB 平面AMN ，
1
2
AN 3
2
sinNMA  
，
AM 2 2 3
1 1
12  
   
2 2
如图，NM 与圆的交点分别为R,S，
当点A位于点R,S时，点A到平面ACB 的距离分别取得最大值和最小值，
1 1 1
学科网（北京）股份有限公司 2   2  3 3 6
且距离的最大值为1 sinNMA1    ，
   
2 2 3 3 6
   
 2   2  3 3 6
距离的最小值为1 sinNMA1    ，
   
2 2 3 3 6
   
 3 6 3 6
所以点A到平面ABC的距离的取值范围是  ,  ，故D错误.
1 1 3 6 3 6
 
三､填空题：本题共 3小题，每小题 5分，共 15分.
r
m
12.1 【解析】展开式的通项为Crx6r   Crmrx62r，
6  x  6
令62r 0解得r 3,C3m3 20.
6
m1.
13.9xay20 【解析】因为 f 3a，所以 f 3 f x f 3x ，
即af x f 3x ，
1 1
令x ，有a f    f 1 ，令x1，
3 3
有a f 1 f 3a，所以 f 11，
1 1  1 1 1
f    ，因为 f x 为偶函数，所以 f     f    ，
3 a  3 3 a
由afx3f3x ，令x1得af13f33a，
所以
f13，
1 1 1 9
令x 得af   3f19，所以 f    ，
3 3 3 a
 1 9
因为 f x 为偶函数，所以 f     ，
 3 a
学科网（北京）股份有限公司 1  1 1 9 1
所以 f x 在点  , f   处的切线方程为y   x ，
 3  3 a a 3
即9xay20.
14.（1） 71
（2） 71
【解析】由双曲线方程知a 1,b 3,c2，如下图所示：
由FA AB，则 AF 2  AF 2  FF 2 16，
1 1 2 1 2
 2
故 AF  AF 2 AF AF 16，
1 2 1 2
而 AF  AF 2a 2，所以 AF AF 6，
1 2 1 2
2
故 AF 2 AF 60，
2 2
解得 AF  7 1，所以 AF  7 1，
2 1
若G为VABF内切圆圆心且FA AB可知，
1 1
以直角边切点和G,A为顶点的四边形为正方形，
1 1
   
结合双曲线定义内切圆半径r  AF  AB  BF  AF  AF  BF  BF
2 1 1 2 1 2 2 1
1  1 
所以r  2 7 BF  BF  2 72  71；
2 2 1 2
即VABF内切圆的半径为 71；
1
故答案为： 7 1, 7 1；
四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤.
学科网（北京）股份有限公司15. 【解析】（1）根据题意可得 3acosCcsinA 3b，
由正弦定理得 3sinAcosCsinAsinC  3sinB，
又 3sinB 3sinAC 3sinAcosC 3cosAsinC，
故sinAsinC  3cosAsinC，
又sinC 0，所以sinA 3cosA，则tanA 3，
π
因为A0,π ，所以A .
3
（2）因为S S S ，
VABC VABM VMCM
1 1 1
所以 bcsinBAC  AM csinBAM  AM bsinCAM ，
2 2 2
1 π
又AM 平分BAC，所以BAM CAM  BAC  ，
2 6
1 3 1 2 2 1 1 2 2 1
所以 bc   c   b ，
2 2 2 3 2 2 3 2
2 2 2 2
则 3bc bc,即bc bc
3 3 3
由余弦定理得a2 b2 c2 2bccosBAC，即16b2 c2 bc，
2 2
所以16(bc)2 3bc(bc)2  bc，解得bc2 6 （负值舍去），
3
故VABC的周长为2 64.
1
16.【解析】（1）取BE的中点N ，连接AN,MN ，则MN ∥ BC且MN  BC，
2
1
又Q AD∥ BC且AD BC,MN ∥ AD且MN  AD.
2
ANDM 为平行四边形，DM ∥ AN.
又DM 平面ABE,AN 平面ABE,DM ∥平面ABE.
（2）取AD中点为F ，连接OF ，因为ABCD为等腰梯形，所以OF  BC，
学科网（北京）股份有限公司又平面ABCD平面BCE ，平面ABCD平面BCE  BC,OF 平面ABCD，
所以OF 平面BCE ，
过点O作直线BC的垂线交B » C于点G，
分别以OG,OC,OF 所在直线为x轴，y轴，z 轴建立如图所示的空间直角坐标系.
1
QBC为直径，BE  BC,BCE 30o,BOE 60o,EOG 30o.
2
2
42
在等腰梯形ABCD中，AB AD DC 2,BC 4，所以OF  22   3，
 
 2 
     
E 3,1,0 ,C0,2,0,D 0,1, 3 ,B0,2,0,A 0,1, 3 ，
uuur uuur uuur uuur
       
CE  3,3,0 ,CD 0,1, 3 ,BE  3,1,0 ,BA 0,1, 3 .
r
设平面DCE的法向量为mx,y,z
，
uuur
r
 mCE 0   3x3y 0
则r uuur , ，令y  3则x3,z 1.
 mCD0 y 3z 0
r  
m 3, 3,1 ，
uuur
r
r  nBE  3ab0
设平面ABE的法向量为n a,b,c ，则r uuur ，
nBA 3cb0
r  
取n  1, 3,1 ，
设平面ABE与平面CDE所成的角为，
r r
mn 65
则cos r r  ，
m n∣ 65
65
平面ABE与平面CDE所成角的余弦值为 .
65
3
17.【解析】（1）据题意，每位游客只游览冰雪大世界的概率为 ，得到1份文旅纪念品；既游览冰雪大世
4
学科网（北京）股份有限公司1
界又参观群力音乐公园大雪人的概率为 ，获得2份文旅纪念品，则X 的可能取值为3,4,5,6，
4
3
3 27
其中PX 3  ，
 
4 64
2
1 3 27
PX 4C1   ，
 
3 4 4 64
2
1 3 9
PX 5C2   ，
 
3 4 4 64
3
1 1
PX 6  ，
 
4 64
所以X 的分布列为
X 3 4 5 6
27 27 9 1
P
64 64 64 64
27 27 9 1 15
EX3 4 5 6  .
64 64 6 64 4
（2）因为n个游客得到文旅纪念品的总个数恰为n1个，
则只有1人既游览冰雪大世界又参观群力音乐公园大雪人，
n1 n
1 3 n 3
于是a C1     ，
   
n n 4 4 3 4
1 3 3 2 3 3 3 n
则S  1 2   3   L n   ，
n 3 4 4 4 4 
3 1 3 2 3 3 3 4 3 n 3 n1
于是 S  1   2   3   L n1   n   ，
4 n 3 4 4 4 4 4 
1 13 3 2 3 3 3 n 3 n1
两式相减，得 S         L    n   
4 n 3 4 4 4 4 4 
 3 3 n 
 1    
1 4 4  3 n1  1 3 n1
  n   1 n4   ，
3
 1
3 4

3 4
 4 
 
n
3
所以S 4n4   .
n 4
（3）设只游览冰雪大世界的人数为x，
学科网（北京）股份有限公司则既游览冰雪大世界又参观群力音乐公园大雪人的人数为100x，
因此游客得到纪念品的总个数n x2100x200x，
x 100x
3 1 1
此时b Cx  Cx 3x，
   
n 100 4 4 4100 100
 1 1
Cx 3x  Cx13x1
 4100 100 4100 100
假定b 取最大值，必有0 x100，于是 ，
n 1 1
 Cx 3x  Cx13x1
4100 100 4100 100
 100! 100!
3


x!100x! x1!99x! x13100x
即 ，整理得 ，
 100! 100!  3101x x
3 
 x!100x! x1!101x!

299 303
解得  x ，而xN，则x75，
4 4
所以当b 取最大值时，n125.
n
18.【解析】（1）根据题意，蒙日圆的半径为 13，所以a2 b2 13.
因为 PP 2，可知b1，则a2 3，
1 2
x2
所以椭圆E的标准方程为  y2 1，
12
 1
因为直线l 过点Q  0, ，可知直线l 的斜率存在，且直线l 与椭圆必相交，
1  2 1 1
1
可设直线l : y kx ,Ax ,y ,Bx ,y ，
1 2 1 1 2 2
 1
y kx

联立方程   2 ，消去y可得  12k2 1  x2 12kx90，
x2
  y2 1
12
12k 9
由根与系数的关系可得：x x  ,x x 
1 2 12k2 1 1 2 12k2 1
y 1 y 1
因为P0,1,P 0,1 ，可得直线AP : y  1 x1，直线BP : y  2 x1，
1 2 1 x 2 x
1 2
学科网（北京）股份有限公司y 1  1 1 1 1
所以 y1  1 x 1  x 2 y 1 1  x 2   kx 1  2    kx 1 x 2  2 x 2  kx 1 x 2  2 x 1 x 2  2 x 1
y1 y 1 x y 1  3 3 3
2 1 2 x  kx   kx x  x kx x  x
x 1  2 2 1 2 2 1 1 2 2 1
2
9k 1  12k  1 3k 1
       x   x
12k2 1 2  12k2 1 2 1 12k2 1 2 1 1
   .
9k 3 9k 3 3
  x   x
12k2 1 2 1 12k2 1 2 1
y1 1
即  ，解得y 2，
y1 3
所以直线AP,BP 的交点P在直线y 2上.
1 2
（2）设直线l 与直线AP,BP的交点分别为Cx ,y ,Dx ,y  ，
2 1 1 3 3 4 4
y 1 y 1
则由（1）可知：直线AP : y  1 x1，直线BP : y  2 x1.
1 x 1 x
1 2
 y 1  y 1
y  1 x1 y  2 x1
 
 x  x
联立方程 1 和 2 ，
 1  1
y  x3 y  x3
 2  2
4x 4x
解得x  1 ,x  2
3 2k1x 1 4 2k1x 1
1 2
 12k  2 36 6 16k2 1
因为 x x  x x 2 4x x     ，
 
1 2 1 2 1 2  12k2 1 12k2 1 12k2 1
0216 4 5
又因为点P到直线l 的距离d   ，
1 2
5 5
1 2 5
可得S  CD d  CD ，只需求 CD 的最小值.
2 5
2
 1 5 4x 4x
由弦长公式可得 CD  1  x x  1  2
 
 2 3 4 2 2k1x 1 2k1x 1
1 2
x x x x
2 5 1 2 2 5 1 2
2k1x 12k1x 1 (2k1)2x x 2k1x x 1
 1  2  1 2 1 2
3 5 16k2 1
  .
2 3k1
学科网（北京）股份有限公司t1
令3k1t，则k  .
3
3 5 16k2 1 5 16(t1)2 9 5 1 16 2 169 5 12 6 5
可得      25        ，
2 3k1 2 t2 2 t 25 25 2 5 5
1 16 3
当且仅当  ，即k  时等号成立.
t 25 16
6 5 12
即 CD 的最小值为 ，可得VPCD面积的最小值为 .
5 1 5
12
故直线AP,BP,l 围成的三角形面积的最小值为 .
1 1 2 5
ax
19.【解析】（1）由 f xlnx1,Rx ，有 f 0 R0 ，
1bx
1 1 a 2ab
可知 fx , fx ,Rx ,Rx ，
x1 (x1)2 (1bx)2 (1bx)3
a 1 1
由题意， f0 R0, f0 R0 ，所以 ，所以a1,b .
2ab1 2
2x 2x
（2）由（1）知，Rx ，令x f xRxlnx1 (x1)，
x2 x2
1 4 x2
则x   0，
x1 (x2)2 x1(x2)2
所以x 在其定义域 1, 内为增函数，又0 f 0R00，
x0时，x f xRx00；
1 x0时，x f xRx00；
所以x0时， f x Rx ；
1 x0时， f x Rx .
f x 1  1 
（3）由hx   m  f x  m  lnx1 ，
Rx 2   x 
学科网（北京）股份有限公司1 1  1 mx2 xx1lnx1
hx lnx1  m   .
x2  x  x1 x2x1
f x 1 
由hx   m  f x 在 0, 上存在极值，
Rx 2 
所以hx
在
0,
上存在变号零点.
令gxmx2 xx1lnx1
，
1
则gx2mx1

lnx11

2mxlnx1,gx2m
.
x1
（1）m0时，gx0,gx 为减函数，gx g00，
gx
在
0, 上为减函数，gx g00，无零点，不满足条件.
1
（2）当2m1，即m 时，gx0,gx 为增函数，gx g00，
2
gx
在
0, 上为增函数，gx g00，无零点，不满足条件.
1 1
（3）当02m1，即0m 时，令gx0即2m ，
2 x1
1
x 1.
2m
1
当0 x 1时，gx0,gx 为减函数；
2m
1
x 1时，gx0,gx 为增函数，
2m
 1   1   1 
g' x g

1

2m

1

ln

11

12mln2m；
min 2m  2m  2m 
1
令Hx1xlnx,0 x1,Hx1 ，
x
1
Hx1 0在0 x1时恒成立，
x
Hx
在
0,1 上单调递增，Hx H10，
 1 
g

1

12mln2m0恒成立；
2m 
Qx0,0m1，
xm10，
则mx2 1mx2 1mxxx1mx1 ，
学科网（北京）股份有限公司mx2 1
 mx1，
x1
mx2 1
1 lnx1mxlnx1；
x1
mx2 x 
Qgxx1

lnx1
，
 x1 
mx2 x mx2 1
令lx lnx11 lnx1mxlnx1mx1lnx1m，
x1 x1
令Fxlnx12 x1(x0),
1 1 1 x1
Fx   0，
x1 x1 x1
则Fx
在
0, 是单调递减，Fx F02，
所以lnx12 x1，
lxmx12 x1m
m m 
 x1m x12 x1 ，
 
2 2 
16 16
令x 1，则x1 ，
m2 m2
m m 8  1
 x12 x10, x1m m0  0m .
2 2 m  2
16 
lx0，即l

1

0.
m2 
 1   1 16 
由零点存在定理可知，lx 在 1, 上存在唯一零点x   1, 1 ，
2m  0 2m m2 
1
又由（3）知，当0 x 1时，gx0,gx 为减函数，g00，
2m
 1 
所以此时，gx0，在 0, 1 内无零点，
 2m 
gx
在
0,
上存在变号零点，
学科网（北京）股份有限公司 1
综上所述实数m的取值范围为 0, .
 2
学科网（北京）股份有限公司