2024年“江南十校”新高三第一次综合素质检测数学试题答案_2024-2025高三（6-6月题库）_2024年10月试卷_1011安徽省江南十校2024-2025学年高三上学期第一次综合素质检测

2024 年“江南十校”新高三第一次综合素质检测
数 学 答 案
★选择题
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B C A A D B A B AD BCD ABD
★填空题：
7 3
12. 13.8.8 14.
8 3
★解答题：
15.
5
1 5
解：（I）设质点移动到1为事件A，则向左移动2次，向右移动3次，P(A)C2   …………5分
5 2 16
（II）X 的可能取值为0,1,2,3,4,5
1 1 1 5 5 1 10
P(X 0)C0( )5  ，P(X 1)C1   ，P(X 2)C2( )5 
5 2 32 5 2 32 5 2 32
1 10 1 5 1 5 1
P(X 3)C3( )5  ，P(X 4)C4( )5 ，P(X 5)C5  
5 2 32 5 2 32 5 2 32
X 0 1 2 3 4 5
1 5 5 5 5 1
P
32 32 16 16 32 32
…………11分
1 5 5 5 5 1 5
所以期望E(X)0 1 2 3 4 5  …………13分
32 32 16 16 32 32 2
16.
解：（I）∵AB//CD，AB平面ABFE ，CD平面ABFE
∴CD//平面ABFE …………2分
又∵平面ABE与平面CDE交于EF ，CD平面CDE
∴CD//EF …………4分
（II）取AD中点O，连接OE，OB，BD
∵DAB 60，AB  AD 4 ∴△ABD是等边三角形
1由三线合一得：OB  AD …………5分
又∵△ADE 是等腰直角三角形
∴OE  AD
∵平面ADE 平面ABC，平面ADE平面ABC  AD
∴OE 底面ABCD …………6分
∵OB平面ABCD
∴OE OB
故OA，OB，OE三线两两垂直 …………7分
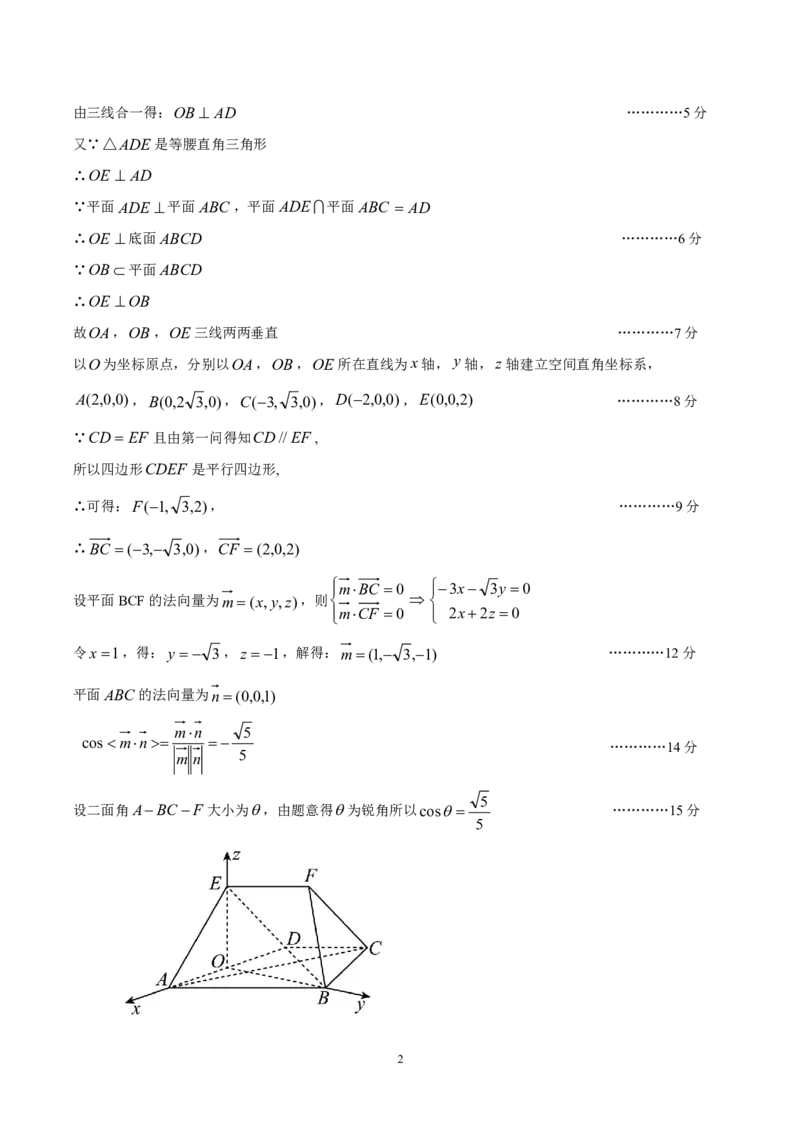
以O为坐标原点，分别以OA，OB，OE所在直线为x轴， y轴，z轴建立空间直角坐标系，
A(2,0,0)，B(0,2 3,0)，C(3, 3,0)，D(2,0,0)，E(0,0,2) …………8分
∵CD  EF 且由第一问得知CD//EF ,
所以四边形CDEF 是平行四边形,
∴可得：F(1, 3,2)， …………9分
∴BC (3, 3,0)，CF (2,0,2)
 mBC 0 3x 3y 0
设平面BCF的法向量为m(x,y,z)，则  
 mCF 0  2x2z 0
令x1，得： y  3，z 1，解得：m(1, 3,1) …………12分
平面ABC的法向量为n(0,0,1)
mn 5
cosmn 
…………14分
m n 5
5
设二面角ABCF大小为，由题意得为锐角所以cos …………15分
5
217.
解：（I） f(x)(x1)ex a， f(x)(x2)ex. …………2分
当x(,2)时， f(x)0， f(x)单调递减；当x(2,)时， f(x)0， f(x)单调递增.
…………3分
①当x1时， f(x)(x1)ex aa0，所以x1时 f(x)无零点； …………4分
②当x1时而 f(1)a0， f(a)(a1)ea a (a1)a 0，
由零点存在定理，x1时， f(x)有唯一零点m(1,a) …………6分
综上， f(x)在R上存在唯一零点.
所以，当x(,m)时， f(x)0， f(x)单调递减；当x(m,)时， f(x)0， f(x)单调递增.
所以 f(x)存在唯一的极值点m. …………7分
（II）由（I）知 f(x)  f(m)，
min
此时 f(m)(m1)em a 0，得a (m1)em,由于a 0，所以m1. …………8分
f(x)b2a等价于b f(x)2a，令h(x) f(x)2a，则
h(x)  f(m) 2a mem am2a mem m(m1)em 2(m1)em (m2 2m2)em，m1
min min
…………10分
令v(x)(x2 2x2)ex,x1
若存在a，使得 f(x)b2a对任意xR成立，等价于bv(x) ， …………11分
max
v(x)(x2 4)ex,x1
当x(1,2)时，v(x)0，v(x)单调递增；当x(2,)时，v(x)0，v(x)单调递减，
所以v(x) v(2)2e2， …………14分
max
 
故b2e2，所以实数b的取值范围 ，2e2 …………15分
318.
解：（I）已知圆M 的圆心为M(1,0)，半径为4；设动圆D的圆心为D(x,y)，半径为R.
DN  R, DM 4R, DM  DN 4 MN,点D的轨迹是以M,N 分别为左右焦点且长轴为4的椭
x2 y2
圆，则曲线C的方程为  1. …………5分
4 3
（II）设P(x ,y ),E(x ,y ),F(x ,y ),H(x ,y ), P(x ,y )，由题意x  x ,y  y ，可知
0 0 1 1 2 2 3 3 0 0 1 2 1 2
x 2 y 2 x 2 y 2
2x  x x ,2y  y  y ， 1  1 1, 2  2 1
3 1 2 3 1 2
4 3 4 3
y  y 3(x x ) 3x
两式相减得k  1 2  1 2  3 , …………7分
EF x x 4(y  y ) 4y
1 2 1 2 3
y 4
而k  3 ，所以k  . …………8分
OH x OH 3k
3 EF
设直线PE的方程为 y y k(xx )，则直线PF 的方程为 y y k(xx )，
0 0 0 0
x2 y2
将PE的方程代入  1得
4 3
（34k2)x2 8k(y kx )x4(y kx )2 120 ①
0 0 0 0
4(y kx )2 12
x x 是方程①的一个根，x x  0 0 ② …………10分
0 0 1 34k2
4(y kx )2 12
同理可得x x  0 0 ③ …………11分
0 2 34k2
16kx y
②③得 x (x x ) 0 0 ④
0 1 2 34k2
8(y 2 k2x 2)24
②③得 x (x x ) 0 0 ⑤
0 1 2 34k2
 
y  y k(x x ) y  k(x x ) y k(x x )2kx kx (x x )2kx 2
k  1 2  1 0 0 2 0 0  1 2 0  0 1 2 0 ⑥
EF x x x x x x x (x x )
1 2 1 2 1 2 0 1 2
8(y 2 k2x 2)
k 0 0 2kx 2
34k2 0 8y 2 246x 2
把④⑤代入⑥，得k   0 0 ⑦
EF 16kx y 16kx y
0 0 0 0
34k2
4x 2 y 2
显然 0  0 1，得8y 2 246x 2 ⑧
0 0
4 3
12x 2 3x
把⑧代入⑦，得k  0  0 …………14分
EF 16kx y 4y
0 0 0
y 4
而k
OP

x
0 ，所以k
OP

3k
…………15分
0 EF
4
又∵k  k k …………16分
OH 3k OP OH
EF
即P,H,O三点共线. …………17分
19.
解：（I）由(n1)a na 1，得 (n2)a (n1)a 1，
n n1 n1 n2
两式相减，得(2n2)a (n1)(a a )，即2a a a ，
n1 n2 n n1 n2 n
 
所以数列 a 是等差数列.
n
 a 3
由 1 ，得a 5，所以公差d a a 2，
2a a 1 2 2 1
1 2
故a a (n1)d 2n1，即a 2n1. …………5分
n 1 n
又因为2n1(n1)2 n2，n1Z,nZ，
 
所以2n1M ,即数列 a 是“平方差数列” …………7分
n
 
（II） b 不是“平方差数列”。 …………8分
n
a  x2  y2 (x y)(x y)，xZ,yZ
①当x,y均为奇数时，x y,x y均为偶数，则a被4整除；
②当x,y均为偶数时，x y,x y均为偶数，则a被4整除；
③当x,y一奇一偶时，x y,x y均为奇数，则a为奇数；
综上，集合M中的元素要么被4整除要么为奇数，
所以b 2M .
1
 
所以 b 不是“平方差数列” …………12分
n
5（III）法一：因为4n(2n1)2 （2n1）2，2n1Z,2n1Z ，所以4nM ,即被4整除的数都属于
M 。
     
令A xx2k1,kZ ，B  xx4k,kZ ，C  xx4k2,kZ ,
结合（I）（II）得，AB  M ，所以所有奇数与被4整除的数都属于M
由题意，c M,c M
i j
①当c ,c 均为奇数时，cc 为奇数，则cc M ；
i j i j i j
②当c ,c 至少有一个被4整除时，cc 被4整除，则cc M ；
i j i j i j
综上，cc M 。 …………17分
i j
法二：由题意，c M,c M
i j
设，c  x 2  y 2,c  x 2  y 2，x ,y ,x ,y Z，则
i 1 1 j 2 2 1 1 2 2
cc (x 2  y 2)(x 2  y 2)(x 2x 2  y 2y 2)(x 2y 2 x 2y 2)
i j 1 1 2 2 1 2 1 2 1 2 2 1
(x 2x 2 2x x y y  y 2y 2)(x 2y 2 2x x y y x 2y 2)
1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 1
(x x  y y )2 (x y x y )2M
1 2 1 2 1 2 2 1
所以，cc M 。 …………17分
i j
6