2022级高三第一学期期中考试数学参考答案_2024-2025高三（6-6月题库）_2024年11月试卷_1122广东省汕头市金山中学2024-2025学年高三上学期期中考试（全科）

2022 级高三第一学期期中考试数学参考答案
1
CADBD BCD ABD ACD BCD xy0, 5,
(ee,)
15．【详解】（1）∵2sinA3sin2C，∴sinA3sinCcosC，
a2b2c2
由正余弦边角关系得，a3c ①，……4分,
2ab
又c2b，②由①②得，a2b3b  a2b24b2 ，∴a2  9 b2,a 3 2 b，∴ a  3 2 ……6分
2 2 b 2
3 2
b
（2）由（1）得， sinA a 2 2 ，
cosC   
3sinC 3c 6b 4
9
b2b24b2
（或由余弦定理得 a2b2c2 2 2 ）……8分
cosC  
2ab 3 2b2 4
14
∵C为锐角，∴sinC ，……9分
4
1 1 3 2 14 3 7
∴ ABC的面积S  absinC  b2  ，∴b2，……11分
2 2 2 4 2
1 3 7
设AB边上的高为h，则 ABC的面积S  chbh ，
2 2
3 7 3 7
∴h ，即AB边上的高为 .……13分
4 4
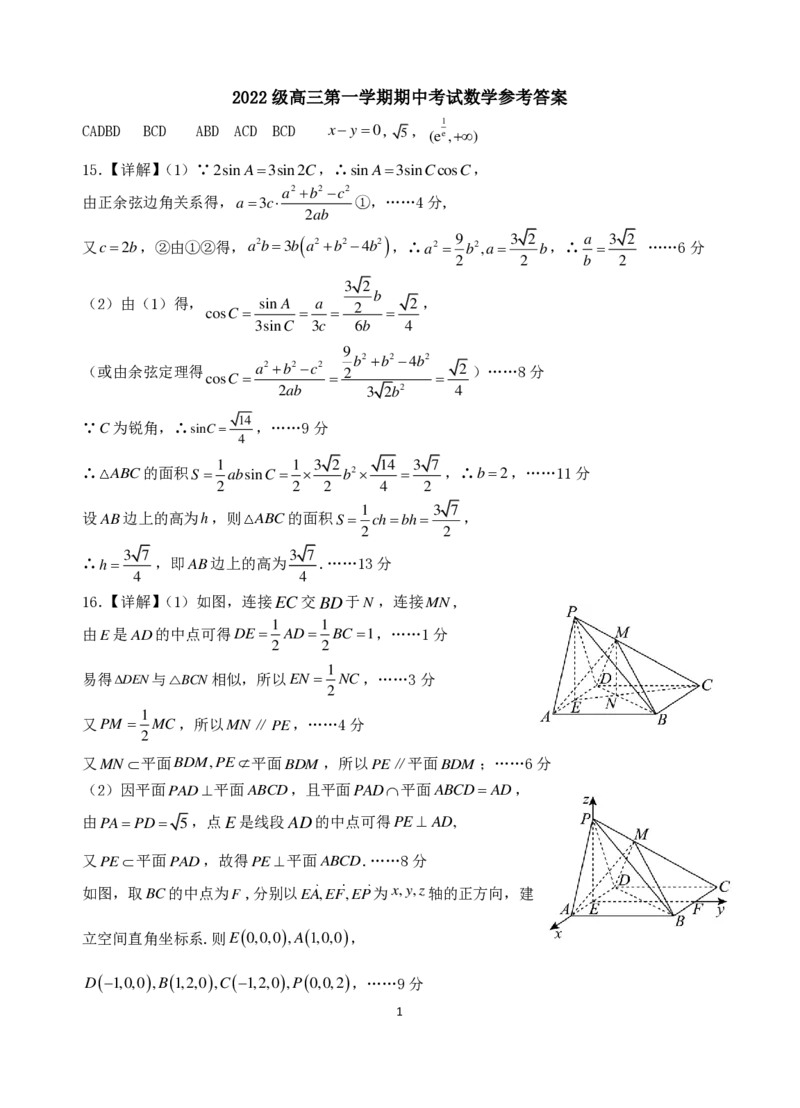
16．【详解】（1）如图，连接EC交BD于N ，连接MN,
1 1
由E是AD的中点可得DE AD BC1，……1分
2 2
1
易得DEN与△BCN相似，所以EN  NC，……3分
2
1
又PM  MC，所以MN∥PE，……4分
2
又MN 平面BDM,PE平面BDM，所以PE∥平面BDM；……6分
（2）因平面PAD平面ABCD，且平面PAD平面ABCDAD，
由PAPD 5，点E是线段AD的中点可得PE AD,
又PE平面PAD，故得PE平面ABCD.……8分
如图，取BC的中点为F,分别以EA,EF,EP为x,y,z轴的正方向，建
立空间直角坐标系.则E0,0,0,A1,0,0，
D1,0,0,B1,2,0,C1,2,0,P0,0,2，……9分
11  1 2 2  1 2 4
PC1,2,2,PM  PC , , ，则M , , ，……10分
3  3 3 3  3 3 3
 4 2 4
设平面AMB的法向量n (x ,y ,z )为，由AB0,2,0,AM  , , ，
1 1 1 1  3 3 3
 n AB2y 0
 1 1
则 4 2 4 ，故可取n 1,0,1；……11分
n AM  x  y  z 0 1
 1 3 1 3 1 3 1
 4 4 4
设平面BDM的法向量为n x ,y ,z ，由BD2,2,0,BM  , , ，
2 2 2 2  3 3 3
 n BD2x 2y 0
 2 2 2
则 4 4 4 ，故可取n 1,1,0.……12分
n BM  x  y  z 0 2
 2 3 2 3 2 3 2
n n
1 1
1 2
故平面AMB与平面BDM的夹角余弦值为 cosn,n     ，……14分
1 2 n n 2 2 2
1 2
π
所以平面AMB与平面BDM 的夹角为 .……15分
3
x2 y2
 1
17．【详解】（1）双曲线3x2  y2 可化为  
3
1 1 2 3 2
S  FF  AB  2  412
ABF1 2 1 2 2   3   3 ，即3
3
y2
双曲线C的标准方程为x2 1．……4分
3
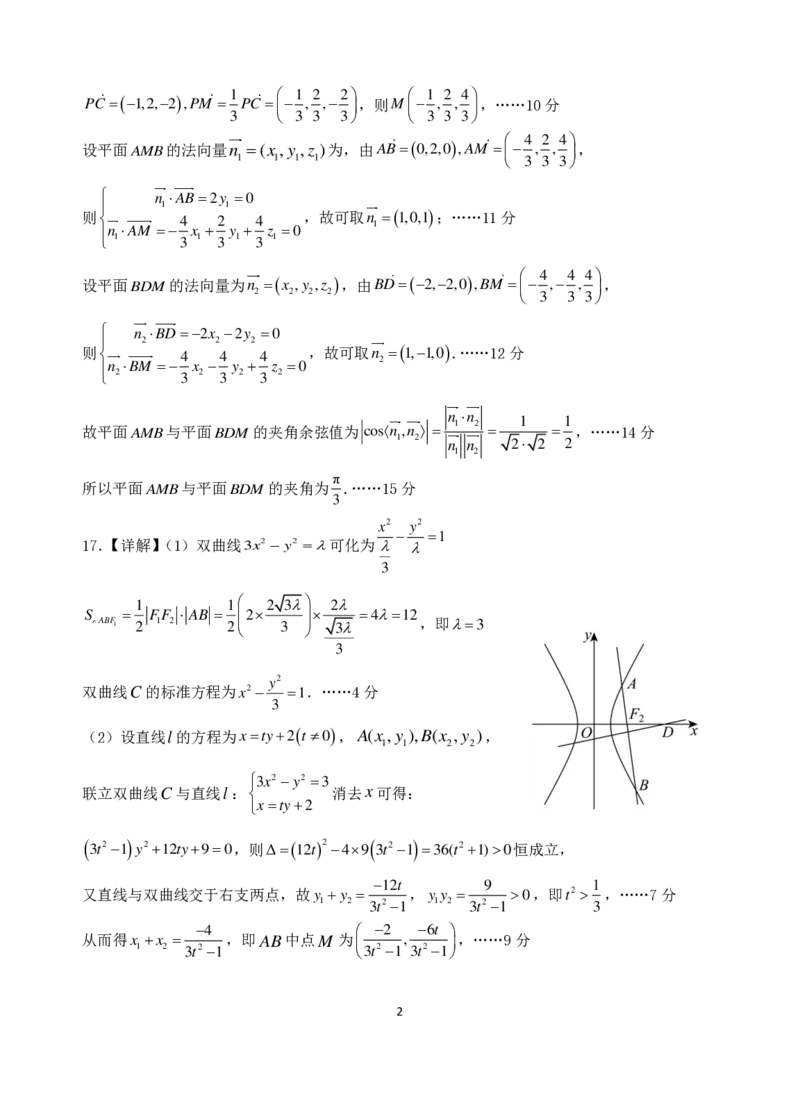
（2）设直线l的方程为xty2t0，A(x,y ),B(x ,y )，
1 1 2 2
3x2y2 3
联立双曲线C与直线l： 消去x可得：
xty2
 3t21  y212ty90，则Δ12t2 49  3t21  36(t21)0恒成立，
12t 9 1
又直线与双曲线交于右支两点，故y y  ，y y  0，即t2  ，……7分
1 2 3t21 1 2 3t21 3
4  2 6t 
从而得x x  ，即AB中点M 为 , ，……9分
1 2 3t21 3t21 3t21
26t  2   8 
线段AB的中垂线为y tx ，则D ,0，……11分
3t21  3t21 3t21 
8 6t26
即 DF  2  ．……12分
2 3t21 3t21
AB  1t2 y y 2 4y y  1t2   12t   2 4 9  6t26 ．……14分
1 2 1 2 3t21 3t21 3t21
DF
即 2 为定值1．……15分
AB
1 1 a x2ax1
18．【详解】（1） f xx alnx， fx1   (x0)……1分
x x2 x x2
若a240时，即2a0时， f(x)0， f x在(0,)单调递增 ……3分
若a240，即a2时，
hxx2ax1有两个零点x  a a24 ，x  a a24 且x 0，x 0，x x ，
1 2 2 2 1 2 2 1
当0xx 时，hx0， fx0， f x单调递增
1
当x xx 时，hx0， fx0， f x单调递减
1 2
当xx 时，hx0， fx0， f x单调递增 ……6分
2
综上所述，当2a0时， f x在在(0,)单调递增；
 a a24 a a24 
当a2时， f x在0, 和 ,上单调递增，
 2   2 
   
a a24 a a24
f x在 , 上单调递减 ……7分
 2 2 
 
1 1 a
（2）因为 f xx alnx，所以 fx1  ，
x x2 x
1 a 1 a
所以k k  fx  fx     2， ……8分
1 2 1 2 x2 x x2 x
1 1 2 2
1 1
x  alnx x  alnx
f x  f x  2 x 2 1 x 1 1 lnx lnx ， ……9分
k  2 1  2 1 1 a 2 1
3 x x x x xx x x
2 1 2 1 1 2 2 1
31 a 1 a 2 lnx lnx
要证k k 2k ，只需证     2a 2 1 ，
1 2 3 x2 x x2 x xx x x
1 1 2 2 1 2 2 1
1 1 2  1 1 lnx lnx 
即证   a  2 2 10， ……11分
x2 x2 xx x x x x 
1 2 1 2 1 2 2 1
x x 3 3 x x x 
不妨设x x 0，则只需证 2  1   a 2  1 2ln 2 0，
2 1 x2 x2 x x  x x x 
1 2 2 1 1 2 1
1 x x2 3x  x x x 
即证  2  1  1 3a 2  1 2ln 2 0，
x  x x2 x   x x x 
1 1 2 2 1 2 1
x 1  1 3   1 
设 2 t(t1)，则只需证 t  3at 2lnt0①，……13分
x x  t2 t   t 
1 1
1
由（1）可知 f xx 2lnx在0,上单调递增，
x
1
则当x1,时， f x f 10，所以t 2lnt0，
t
1 3 2 3 t33t2 (t1)2t2
设gtt  3，则gt1    0，
t2 t t3 t2 t3 t3
所以gt在1,上单调递增，所以gtg10，……15分
又因为0x 1,a1，所以要证①，
1
1 3 1 4 1
只需证t  3t 2lnt2lnt  30，
t2 t t t t2
4 1 2 4 2 2 1 2
设ht2lnt  3，则ht    1  0，
t t2 t t2 t3 t  t
所以ht在1,上单调递增.所以hth10，得证. ……17分
1 8 1 1 8 1
19．【详解】（1）由题：令n1,则 a b  ，即 b  ，故  b  ，
1 1 2 3 1 2 2 3 1 2
13 19
得 b  ，又b Z,b 3，同理可得，b 5,b 7. ……3分
6 1 6 1 1 2 3
1 1 1 1 1
（2）由题意 a b  ，故a  b a  ,a  b a  ，
n n 2 n 2 n n 2 n1 2 n1 n1 2
从而a a 1b b a a 1，即1b b d 1，……6分
n1 n n1 n n1 n n1 n
因为b Z,dZ，所以b b d 0,即b b d，故数列b 是等差数列. ……7分
n n1 n n1 n n
49 57 9 3
（3）因为a  a  ,则a  a ，解得 ，
n1 10 n 20 n1 10 n 2
3 81  3 81 9
又a   0，故a  是以 为首项，公比为 的等比数列，
1 2 100  n1 2 100 10
3 81  9  n1  9  n1 3
则a     ，即a    ，……9分
n 2 100  10 n  10 2
3 81   9  n
从而S  n 1   ……10分
n 2 190  10 
 9  n1 3  9  n1 3
当n为奇数时，a    ，易知a    单调递减，
n 10 2 n 10 2
3 231 1 31
故 a a  ，得a 2( , ]，则有b 2；……12分
2 n 1 100 n 2 100 n
 9  n1 3  9  n1 3
当n为偶数时，a    ，易知a    单调递增，
n 10 2 n 10 2
3 771 3 229 1
故a a  ，即 a  ，得a 1[ , )，则有b 1；
2 n 2 1000 n 2 n 1000 2 n
1,n为偶数
综上，b  ，……14分
n 2,n为奇数
3 81   9  n  9  n
当n为偶数时，T n  2 n，由S n T n ，得 190   1 10     0,即  10   1，无解；……15分
3n1 3n1
当n为奇数时，T T b  1 ;
n n1 n1 2 2
81   9  n 1  9  n 14
由S n T n ,得 190   1 10      2 ,即  10    81 ，
14
故n>log 16.7，所以存在正整数n，使得S T ，正整数n的最小值为17. ……17分
9 81 n n
10
5