2022级高三第一学期期中考试数学试卷_2024-2025高三（6-6月题库）_2024年11月试卷_1122广东省汕头市金山中学2024-2025学年高三上学期期中考试（全科）

2022 级高三第一学期期中考试 数学试卷 命题人：肖冬璇 审题人：袁明星 一、选择题：本大题共 8小题，每小题5分，共 40分．在每小题给出的四个选项中，只有一项 是符合题目要求的． 1．设全集U {1,2,3,4,5}，集合M 满足C M 2,4，则（ ） U A．1M B．4M C．5M D．3M 2．设0,，则“  ”是“sin 3 ”的（ ） 3 2 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 3．设等差数列a 的公差不为0，若a ，a ，a 构成等比数列，a 6，则a （ ） n 4 5 7 6 7 A．5 B．6 C．7 D．8 3 1 4．已知sin2 ，则tan （ ） 4 tan 8 8 4 1 A． B． C． D． 3 3 3 2 5．若aln 10,b ln2ln5,cln 4e，则a、b、c的大小关系是（ ） A．cab B．abc C．cba D．bac 6．国家速滑馆又称“冰丝带”，是北京冬奥会的标志性场馆，拥有亚洲最大的全冰面设计，但 整个系统的碳排放接近于零，做到了真正的智慧场馆、绿色场馆，并且为了倡导绿色可循环的理 念，场馆还配备了先进的污水、雨水过滤系统，已知过滤过程中废水的污染物数量Nmg/L与 时间t（小时）的关系为N N ekt（N 为最初污染物数量，且N 0）.如果前4个小时消除了 0 0 0 20%的污染物，那么污染物消除至最初的64%还需要（ ） A．3.8小时 B．4小时 C．4.4小时 D．5小时  π π π π  7．已知函数 f(x)sin(2x) 满足 f   f  ，若 f x在区间 ,t  上恰有3个零  2 4 3 2  点，则实数t的取值范围为（ ） 25π 37π 25π 49π 37π 49π 37π 49π A．  ,  B．  ,  C．  ,  D． ,   24 24   24 24   24 24   24 24  数学第1页（共4页）8．定义在R上的函数 f x满足 f xg2xg42x且 f 21，函数 f(x2)为偶函数，则 下列说法不正确的是（ ） A． f(x)的图象关于(1,0)对称 B． f(x)的图象关于x2对称 22 C．4是 f x的一个周期 D． f(k)0 k1 二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目 要求．全部选对的得6分，部分选对的得部分分，有错选的得0分． 9．已知关于x的不等式ax2bxc0的解集为(,2)(3,)，则下列选项中正确的是（ ） A．a0 B．不等式bxc0的解集是 x x6  1 1  C．abc0 D．不等式cx2bxa0的解集为,  ,  3 2   π 10．已知函数 f x2sin2x 3，则下列说法正确的是（ ）  6 A． f x的值域为1,5  π kπ  B． f x的对称中心为  ,0,kZ 12 2  C． f x在  0, π 上的递增区间为  0, π   2  3  5  D． f x在0, π上的极值点个数为1  6  11．设等比数列a 的公比为q，前n项积为T ，下列说法正确的是（ ） n n A．若T T ，则a a 1 8 12 10 11 B．若T T ，则T 1 8 12 20 10 C．若a 1 1024，且T 10 为数列T n 的唯一最大项，则   1  9 q 1 2 2 D．若a 0，且T T T ，则使得T 1成立的n的最大值为20 1 10 11 9 n 三、填空题：本题共3小题，每小题5分，共15分． 12.已知函数 f xxex，则 f x在 0, f 0 处切线方程为 ． c b 13．在ABC中，角A,B,C所对的边分别为a,b,c，若a2 bcsinA，则  的最大值为 ． b c 数学第2页（共4页）14．已知函数 f(x)xalog x(a1,b1)有且只有一个零点，则ab的取值范围为 . 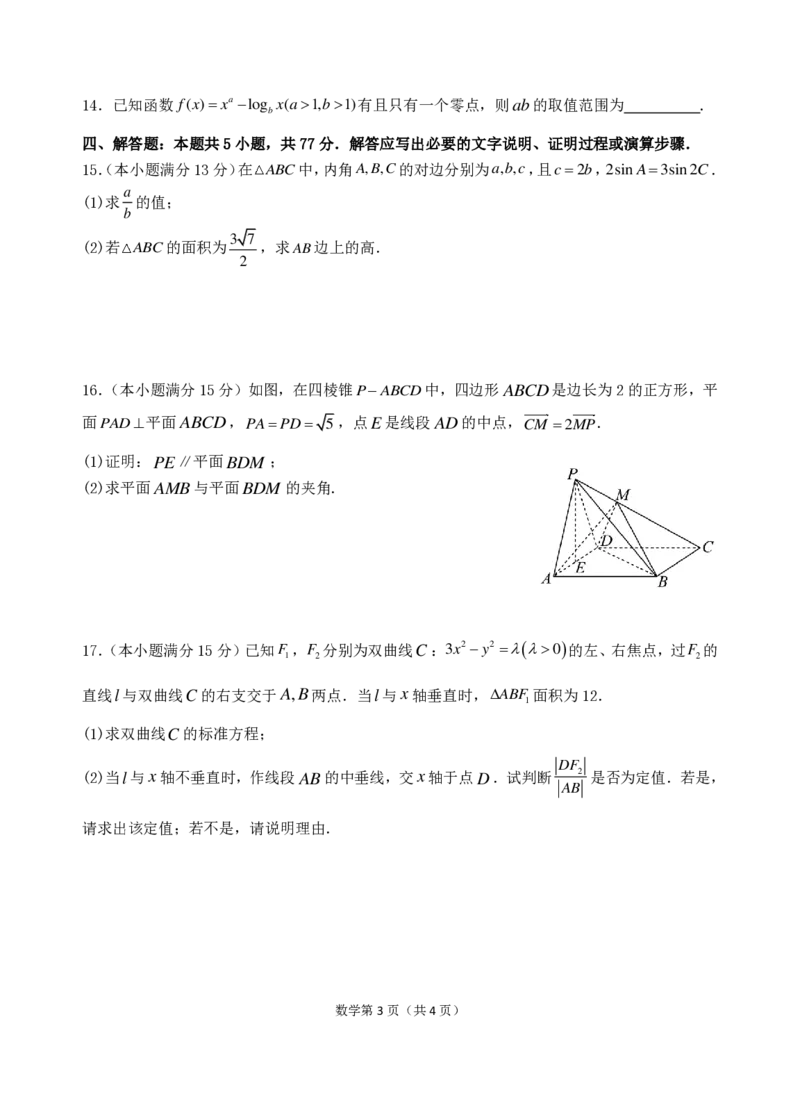b 四、解答题：本题共5小题，共77分．解答应写出必要的文字说明、证明过程或演算步骤． 15．（本小题满分13分）在 ABC中，内角A,B,C的对边分别为a,b,c，且c2b，2sinA3sin2C． a (1)求 的值； b 3 7 (2)若 ABC的面积为 ，求AB边上的高． 2 16．（本小题满分15分）如图，在四棱锥PABCD中，四边形ABCD是边长为2的正方形，平 面PAD平面ABCD，PAPD 5，点E是线段AD的中点，CM 2MP. (1)证明：PE∥平面BDM ； (2)求平面AMB与平面BDM 的夹角. 17．（本小题满分15分）已知F ，F 分别为双曲线C：3x2y2 0的左、右焦点，过F 的 1 2 2 直线l与双曲线C的右支交于A,B两点．当l与x轴垂直时，ABF 面积为12． 1 (1)求双曲线C的标准方程； DF (2)当l与x轴不垂直时，作线段AB的中垂线，交x轴于点D．试判断 2 是否为定值．若是， AB 请求出该定值；若不是，请说明理由． 数学第3页（共4页）1 18．（本小题满分17分）已知函数 f xx alnx. x (1)当a0时，讨论 f x的单调性； (2)记曲线y f x在Px, f x  ，Qx , f x  两点处的切线斜率分别为k ,k ，直线PQ的斜 1 1 2 2 1 2 率为k ，其中x,x 0,1，求证：当a1时，有k k 2k . 3 1 2 1 2 3 1 19．（本小题满分17分）如果数列x ,y ，其中y Z，对任意正整数n都有 x y  ，则 n n n n n 2 称数列y 为数列x 的“接近数列”．已知数列b 为数列a 的“接近数列”． n n n n 2 (1)若a 2n  nN* ，求b,b ,b 的值； n 3 1 2 3 (2)若数列a 是等差数列，且公差为ddZ，求证：数列b 是等差数列； n n 231 9 57 (3)若数列a 满足a  ，且a  a  ，记数列a ､b 的前n项和分别为S ,T ， n 1 100 n1 10 n 20 n n n n 试判断是否存在正整数n，使得S T ？若存在，请求出正整数n的最小值；若不存在，请说明 n n 14 理由．（参考数据：log 16.7） 9 81 10 数学第4页（共4页）