2024-2025-1学期高三年级11月考数学答案(1)_2024-2025高三（6-6月题库）_2024年12月试卷_1211甘肃省兰州第一中学2024-2025学年高三上学期12月月考试题

兰州一中高三年级 11 月月考试题
高三数学答案
一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目
要求的.）
题号 1 2 3 4 5 6 7 8
答案 D A C A B C C D
二、多选题(本大题共3小题，每小题6分，共18分.全部选对的得6分，部分选对的得部分分，第9题
答对一个选项得2分；第10、11题答对一个选项得3分,有选错的得0分.)
题号 9 10 11
答案 AD ABD ABD
三、填空题(本大题共3小题，每小题5分，共15分.)
133 π
12. 3x+y30； 13. ； 14.
66 3
四、解答题(本大题共5小题，共77分.解答应写出必要的文字说明、证明过程或演算步骤.)
15.(13分)【解析】（1）因为b (a a )b ，a 1，a 3，
n n1 n n1 1 2
令 n1 得2b b ，
1 2
又数列 b 为等比数列，所以公比为2，即b 2b ，
n n1 n
则a a 2，所以数列 a 是以1为首项2为公差的等差数列，所以a 2n1……………6分
n1 n n n
（2）由（1）知数列
b
为公比为2的等比数列
n
若选①，由2S S 2得2  b 2b b 2b 4b 2，所以b＝2，则b 2n
2 3 1 1 1 1 1 1 n
若选②，由b ，2a ，b 成等差数列得4a b b ，即2b 8b 20，所以b 2，则b 2n
2 3 4 3 2 4 1 1 1 n
b(126)
若选③，由S 126得 1 126 ，所以b 2，则b 2n
6 12 1 n
2n1,n为奇数,
所以c  ，
n 2n,n为偶数,
数列
c
的奇数项是以1为首项4为公差的等差数列，偶数项是以4为首项4为公比的等比数列，
n
所以T  a a a  b b b 
2n 1 3 2n1 2 4 2n
n(n1) 4(14n) 4(4n1)
= n 4 =2n2n ………………13分
2 14 3
兰州一中高三年级11月月考试卷答案 第 1 页 共 4 页
{#{QQABaQgEggCAAhAAARgCUwHgCkAQkgEACYgGBFAMoAAAyRFABAA=}#}16.(15分)【解析】(1)证明：由题意得 PA平面ABC,因为BC平面ABC,所以PABC,
又因为AC BC,PA,AC 平面PAC,所以BC 平面PAC,
又因为BC平面PCB,所以平面PAC 平面PBC. ……………6分
1
(2)因为AC 5,BC 12,AC BC,所以S  12530,
△ABC
2
1
又因为三棱锥PABC的体积为100,即,得100 PA30 PA10,
3
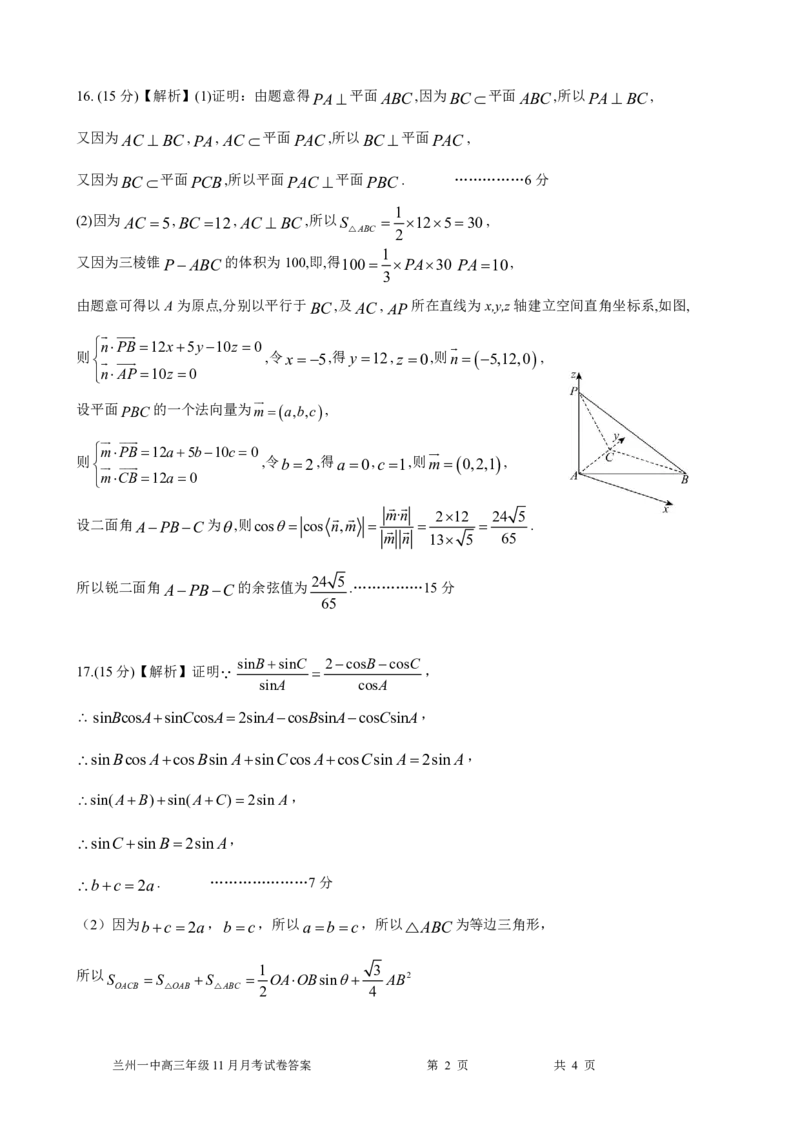
由题意可得以A为原点,分别以平行于BC,及AC,AP 所在直线为x,y,z轴建立空间直角坐标系,如图,
 
 nPB12x5y10z 0 
则   ,令x5,得y 12,z 0,则n5,12,0 ,
nAP10z 0

设平面
PBC
的一个法向量为ma,b,c,
 
 mPB12a5b10c0 
则   ,令b2,得a0,c1,则m 0,2,1 ,
mCB12a0
 
  m·n 212 24 5
设二面角APBC为,则cos cos n,m      .
m n 13 5 65
24 5
所以锐二面角APBC的余弦值为 .……………15分
65
sinBsinC 2cosBcosC
17.(15分)【解析】证明  ，
sinA cosA
sinBcosAsinCcosA2sinAcosBsinAcosCsinA，
sinBcosAcosBsinAsinCcosAcosCsinA2sinA，
sin(AB)sin(AC)2sinA，
sinCsinB2sinA，
bc2a. …………………7分
（2）因为bc2a，bc，所以abc，所以△ABC为等边三角形，
1 3
所以 S S S  OAOBsin AB2
OACB △OAB △ABC 2 4
兰州一中高三年级11月月考试卷答案 第 2 页 共 4 页
{#{QQABaQgEggCAAhAAARgCUwHgCkAQkgEACYgGBFAMoAAAyRFABAA=}#}3 
sin OA2 OB2 2OAOBcos
4
5 3
sin 3cos
4
2sin   π  5 3 ，0,π， π     π , 2π  ，
 3 4 3  3 3 
当且仅当 π  π ，即 5π 时取最大值，S 的最大值为 2 5 3 .…………………15分
3 2 6 OACB 4
18.(17分) 【解析】（1）由题意，
x12 y2

2 ，
x2 2
x2
整理化简得，  y2 1 ，
2
所以曲线C的标准方程为
x2
y2 1. ……………6分
2
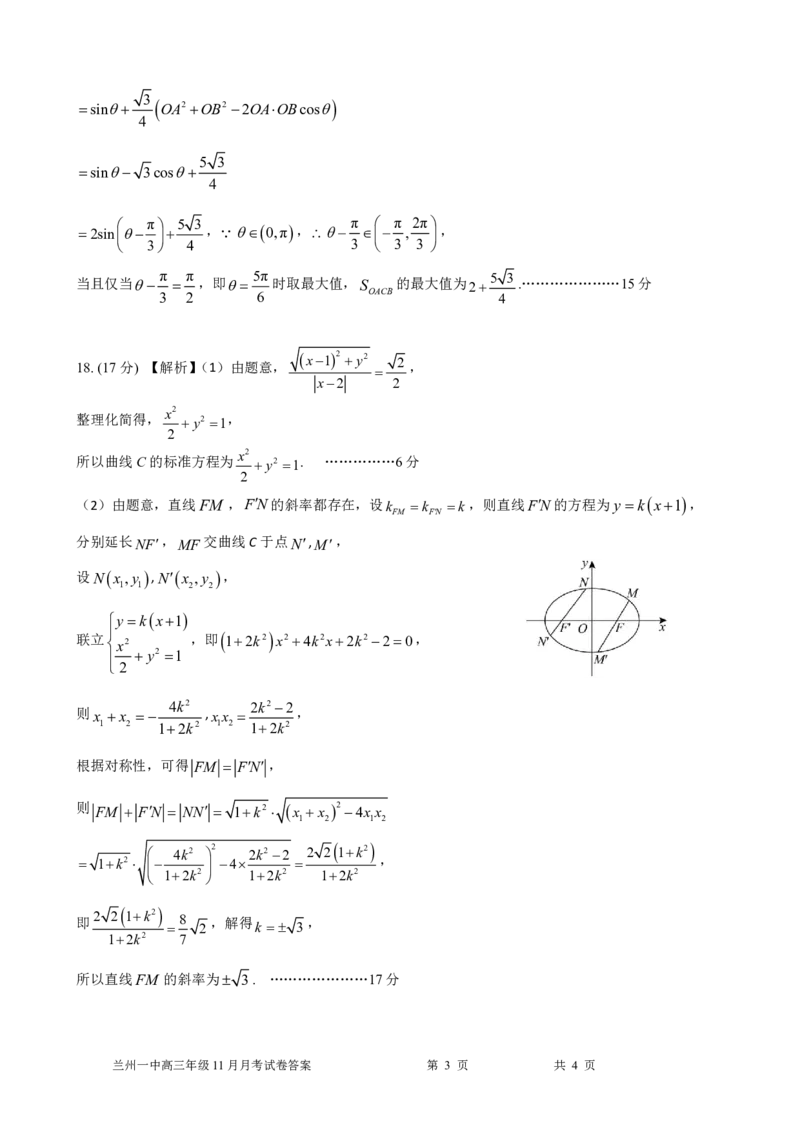
（2）由题意，直线FM ，FN的斜率都存在，设k k k，则直线FN的方程为yk  x1 ，
FM FN
分别延长 NF，
MF
交曲线C于点 N,M，
设Nx,y ,Nx ,y ，
1 1 2 2
ykx1

联立 x2 ，即 12k2 x2 4k2x2k2 20，
  y2 1
 2
4k2 2k22
则 x x  ,x x  ，
1 2 12k2 1 2 12k2
根据对称性，可得 FM  FN，
则 FM  FN  NN  1k2  x x 24x x
1 2 1 2
 1k2 


4k2 

2
4
2k22

2 2  1k2
，

12k2

12k2 12k2
即 2 2
 1k2
8 ，解得 ，
 2 k  3
12k2 7
所以直线FM 的斜率为 3. …………………17分
兰州一中高三年级11月月考试卷答案 第 3 页 共 4 页
{#{QQABaQgEggCAAhAAARgCUwHgCkAQkgEACYgGBFAMoAAAyRFABAA=}#}19.(17分) 【解析】(1)令x  y 0则， f 0 f 02f20，又 f x0，故 f 01.
令x1，y 1，则 f 2 f 02f 1 f 1，
则 f21 25 f 10 故 f 1 5 ……………5分
16 4
5
(2)令xn，y 1，nN ，则 f n1 f n12f n f 1 f n，

2
2f n1 f n2 2f n f n1  ，即a n 2a n1
又a 3，所以数列a 为以2为公比，3为首项的等比数列，即a 3.2n1，
1 n n
a a a 099
则log 1 log 2 log 100 01299 1004950 ……………11分
2 3 2 3 2 3 2
(3)由题意得：函数g  x 定义域为R，定义域关于原点对称，
令x y0，有g0g02g20又g00，故g  0 1.
令x0，y为任意实数则gygy2g0gy
即gygy，故g  x 是偶函数
因为gx ygxy2gxgy 又因为当x0时，g  x 1
所以当x0时，有2gxgy2gy 所以gx ygxy2gy
x ， x 为有理数，不妨设 x  p 1 ， x  p 2
2 1 1 q 2 q
1 2
a b
令N 为 x ， x ，分母的最小公倍数 且 x  ， x  ，a，b均为自然数，且ab，
2 1 1 N 2 N
设 C n  g   N n    ， g01g   N 1    ，则c 0 c 1
令x n ， y 1 ， 则 g   n1 g   n1 2g   n   ，
N N  N   N  N 
即C C 2C ，C 2C C C C C C ，
n1 n1 n n1 n n1 n n n1 n
故数列C 单调递增则g 
x

g

x
，
n 2 1
又gx是偶函数，所以有gx  gx  …………………17分
2 1
兰州一中高三年级11月月考试卷答案 第 4 页 共 4 页
{#{QQABaQgEggCAAhAAARgCUwHgCkAQkgEACYgGBFAMoAAAyRFABAA=}#}