文档内容
明德中学 2024 年上学期入学考试
高一年级数学
试卷时量:120分钟 满分 150命题:高一数学备课组 审定:高一数学备课组
一、单选题(本题共 8个小题,每小题 5分,共 40分,每个小题只有一个正确答案)
1.已知集合M ={ 0,1,2,3 } ,N ={x∣x<2},则M ∩ ( N ) =( )
R
A.
(−∞,2 )
B.
(
2,3
)
C.
{
2,3
}
D.
{
1,2,3
}
2.设m∈R,命题“存在m≥0,使mx2 −mx−1=0有实根”的否定是( )
A.任意m≥0,使mx2 −mx−1=0无实根
B.任意m<0,使mx2 −mx−1=0有实根
C.存在m≥0,使mx2 −mx−1=0无实根
D.存在m<0,使mx2 −mx−1=0有实根
3 4
3.已知角 α 的顶点与坐标原点重合,始边与x轴的非负半轴重合,终边与单位圆交于点P ,− ,那么
5 5
cos
( π+α)
等于( )
4 3 4 3
A.− B. C. D.−
5 5 5 5
4.若实数a,b,c满足ac2 >bc2,m>0,则下列结论中正确的是( )
A.a >b B. a > b
1 1 b b+m
C. < D. <
a b a a+m
3
5.已知 f ( x ) 的定义域是−1, ,则 f ( sin2x ) 的定义域为( )
2
π π π π
A. +2kπ, +2kπ ,k∈Z B. +kπ, +kπ ,k∈Z
6 3 6 3
2π π π 7π
C. − +2kπ, +2kπ ,k∈Z D. +kπ, +kπ ,k∈Z
3 6 3 6
3a
6.关于x的不等式−x2 +4ax−3a2 ≥0(a >0)的解集为 { x∣x ≤ x≤ x } ,则x +x + 的最小值是
1 2 1 2 x x
1 2
( )
学科网(北京)股份有限公司2 6
A.4 B.2 6 C.2 D.
3
7.命题“对任意的m∈[−1,1 ] ,总存在唯一的x∈[
0,3
]
,使得x2 −2x−am−1=0”成立的充分必要条件是
( )
A.−2≤a≤2 B.−1≤a≤1
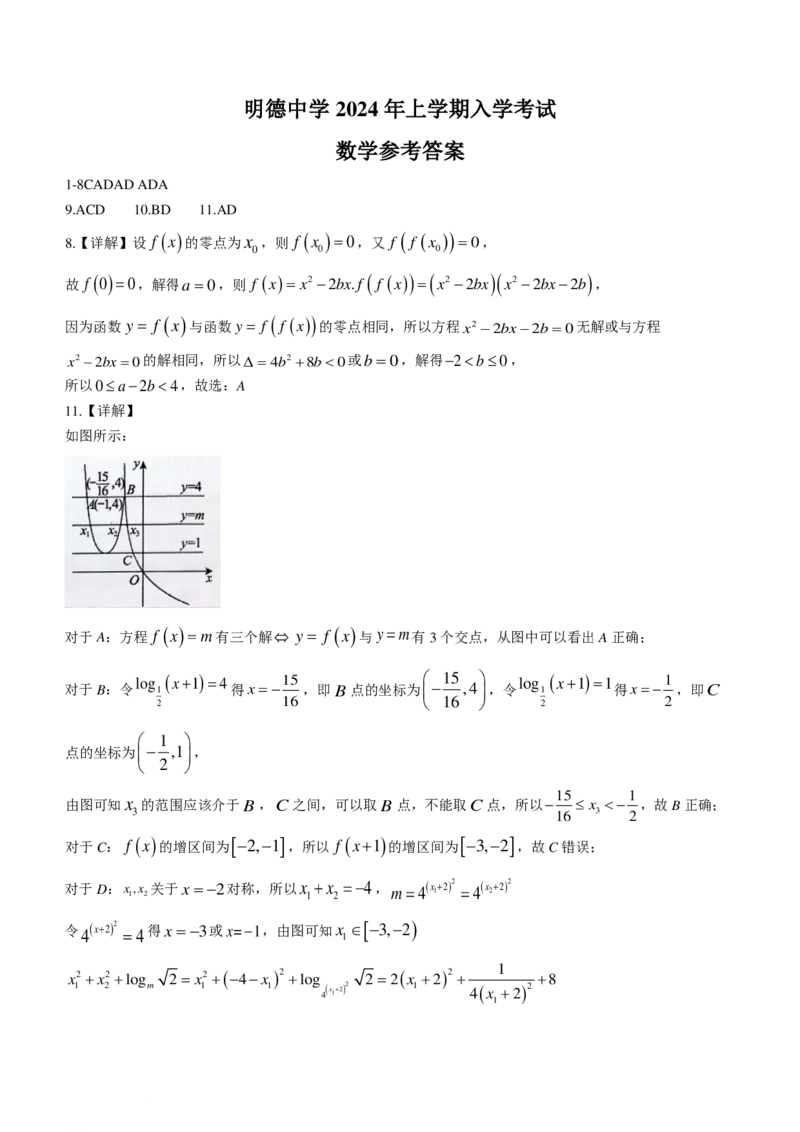
C.00,且a ≠1).
下列说法正确的是( )
A.浮萍每月的增长率为2
B.第5个月时,浮萍面积就会超过30m2
C.浮萍每月增加的面积都相等
D.若浮萍曼延到2m2,3m2,6m2所经过的时间分别是t ,t ,t ,则t +t =t
1 2 3 1 2 3
学科网(北京)股份有限公司 4(x+2)2 ,x≤−1,
11.已知函数 f(x)= 若函数y = f(x)−m有三个零点x ,x ,x ,且x < x < x ,则
log (x+1), x>−1, 1 2 3 1 2 3
1
2
( )
A.10
围是__________.
14.已知 f
(
x
)=sinx+2cosx,当x=θ时,
f
(
x
)
取得最大值,则tanθ=__________.
四、解答题(本题共 5个小题,共 77分,解答应写出必要的文字说明证明过程或演算步骤.)
15.(本小题满分13分)计算下列各式的值:
2
(1)
27
− 3 −
49
0.5 +(0.008) − 2 3× 1 +(π−1)0
8 9 25
1
(2)log 3⋅log 8+(lg5)2 +lg5lg20+ lg16−2log23
2 3 2
16.(本小题满分15分)
sin
( π−α)
已知 f
(α)=
tan
( π+α)
11
(1)求 f π的值;
6
π 1 π
(2)已知 f α+ = ,求sin −α 的值.
3 3 6
17.(本小题满分15分)
学科网(北京)股份有限公司 π 3
已知函数 f ( x )=2cosx⋅sinx− +2 3cos2x− ,x∈R
3 2
( )
(1)求 f x 的对称轴方程;
π π
(2)若关于x的方程3[f ( x ) ]2 +mf ( x )+1=0在区间
− ,
上有两个不相等的实根,求实数m的取值范
6 3
围.
18.(本小题满分17分)
已知函数 f ( x )=log ( 1−x )−log ( b+x )+m(a >0且a ≠1)为奇函数.
a a
( )
(1)求函数 f x 的定义域及解析式;
1 1
(2)若x∈
− ,
,函数 f ( x ) 的最大值比最小值大2,求a的值.
2 2
19.(本小题满分17分)
设正整数n≥4,若由实数组成的集合A={ a ,a ,,a } 满足如下性质,则称 A为H 集合:对 A中任意四
1 2 n n
个不同的元素a,b,c,d ,均有ab+cd∈A.
1 1
(1)判断集合A =0, ,1,2和A = ,1,2,3是否为H 集合,说明理由;
1 2 2 3 4
(2)若集合A={ 0,x,y,z } 为H 集合,求 A中大于1的元素的可能个数;
4
(3)若集合 A为H 集合,求证: A中元素不能全为正实数.
n
学科网(北京)股份有限公司明德中学 2024 年上学期入学考试
数学参考答案
1-8CADAD ADA
9.ACD 10.BD 11.AD
8.【详解】设 f ( x ) 的零点为x ,则 f ( x )=0,又 f ( f ( x )) =0,
0 0 0
故 f ( 0 )=0,解得a =0,则 f ( x )= x2 −2bx.f ( f ( x )) = ( x2 −2bx )( x2 −2bx−2b ) ,
因为函数 y = f ( x ) 与函数y = f ( f ( x )) 的零点相同,所以方程x2 −2bx−2b=0无解或与方程
x2 −2bx=0的解相同,所以Δ=4b2 +8b<0或b=0,解得−20
Δ =m2 −12=0
则需H
(
1
)=3+m+1<0或
m ,
0<− <1
6
解得:m<−4或m=−2 3.
1−x>0
( )
18.【详解】(1)要使函数 f x 有意义,则 ,可得:−b< x<1,
b+x>0
因为 f
(
x
)
为奇函数,所以−b+1=0,即b=1,所以 f(x)的定义域为
(−1,1 )
,
由 f(0)=0可得:m=0,所以 f(x)=log (1−x)−log (1+x),
a a
此时 f (−x )=log ( 1+x )−log ( 1−x )=−f ( x ) , f ( x ) 是奇函数,符合题意.
a a
1−x 2
(2) f(x)=log (1−x)−log (1+x)=log =log −1+ ,
a a a1+x a x+1
①当a >1时,函数y= f(x)单调递减,
学科网(北京)股份有限公司1 3 1
所以 f(x) = f(− )=log −log =log 3,
max 2 a 2 a 2 a
1 1 3 1
f(x) = f( )=log −log =log ,
min 2 a 2 a 2 a 3
1
所以 f(x) − f(x) =log 3−log =log 9=2,解得a=3.
max min a a 3 a
②当00,从而yz∉A,与yz∈A矛盾;
②若x< y<0< z,因为xz < yz < xy,故xz = x,yz = y,xy = z,
学科网(北京)股份有限公司所以z =1,xy =1.
1
经验证,此时A=x, ,0,1是H 集合,元素大于1的个数为0;
x 4
③若x<0< y< z,因为xz < xy <0,所以与
{
x,y,z
}={
xy,yz,xz
}
矛盾;
④若01.经验证,此时A=0,x,1, 是H 集合,元素大于1的个数为1;
x x 4
综上: A中大于1的元素的可能个数为0,1.
(3)假设集合 A中全为正实数.
若A 中至少两个正实数大于1,设0a >1,
1 2 n n n−1
取 { a,b,c,d }={ a ,a ,a ,a } ,则ab+cd =a a +a a ∈A,
n−3 n−2 n−1 n n−3 n−2 n−1 n
而a a +a a >a a >a ,从而a a +a a ∉A,矛盾;
n−3 n−2 n−1 n n−1 n n n−3 n−2 n−1 n
因此 A中至多有1个正实数大于1.
当n=4时,设a 0,
1 2 3 4 1 3 2 4 4 3 2 1 3 2 4 1 3 2
( aa +a a )−( aa +a a )=a ( a −a )−a ( a −a )=( a −a )( a −a )>0,
1 3 2 4 1 4 2 3 2 4 3 1 4 3 4 3 2 1
所以aa +a a >aa +a a >aa +a a >a ,
1 2 3 4 1 3 2 4 1 4 2 3 1
所以aa +a a =a ,aa +a a =a ,aa +a a =a .因为0